平面几何经典难题
平面几何经典难题及解答
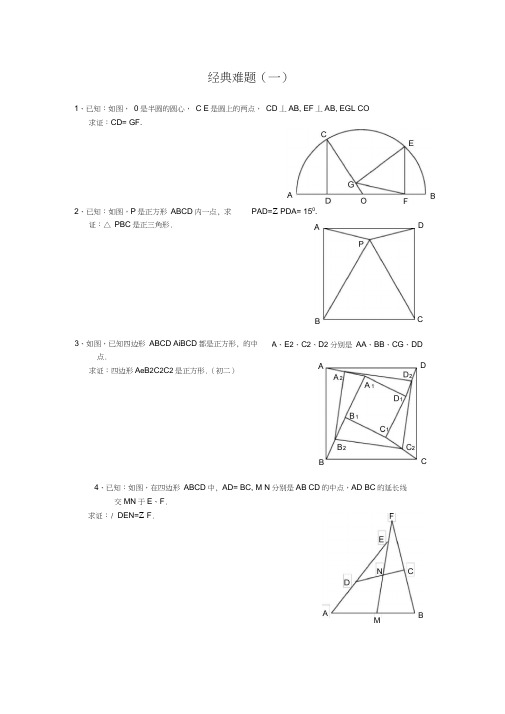
经典难题(一)1、已知:如图, 0是半圆的圆心, C E 是圆上的两点, CD 丄AB, EF 丄AB, EGL CO 求证:CD= GF.4、已知:如图,在四边形 ABCD 中, AD= BC, M N 分别是AB CD 的中点,AD BC 的延长线交MN 于E 、F .求证:/ DEN=Z F .2、已知:如图,P 是正方形 ABCD 内一点, 求证:△ PBC 是正三角形. PAD=Z PDA= 150. 3、如图,已知四边形 ABCD AiBCD 都是正方形, 的中点.求证:四边形A e B 2C 2C 2是正方形.(初二) A 、E 2、C 2、D 2 分别是 AA 、BB 、CG 、DD DCDCM经典难题(二)1、已知:△ ABC 中,H 为垂心(各边高线的交点),0为外心,且 OM L BC 于M.(1) 求证:AH= 20M(2) 若/ BAC= 600,求证: 2、设MN 是圆O 外一直线,过0作OAL MN 于A 自A 引圆的两条直线, 交圆于B 、C 及D E , 直线EB 及CD 分别交MN 于P 、Q. 求证:AP = AQ (初二) 3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC DE 设CD EB 分别交MN 于P 、Q.求证:AP = AQ (初二) 4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形CBFGAH= AO (初二)H EB CM D G ECAM NPO点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)F1、如图,四边形 ABCD 为正方形,求证:CE = CF.(初二)DE// AC, AE = AC, AE 与 CD 相交于 F .2、如图,四边形 ABCD 为正方形,DE// AC,且CE= CA 直线EC 交DA 延长线于F . 求证:AE = AF.(初二) 3、设P 是正方形 ABCD-边BC 上的任一点,PF 丄AP, CF 平分/ DCE求证:PA = PF.(初二)4、如图,PC 切圆0于C, AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线P0相交于 B D.求 证:AB= DC BC = AD (初三)EA DC1、已知:△ ABC 是正三角形,P 是三角形内一点, PA = 3, PB= 4, PC = 5. 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/ PBA=Z PDA 求证:/ PAB=Z PCB (初二)4、平行四边形 ABCD 中,设E 、F 分别是BC AB 上的一点,AE 与CF 相交于P ,且 AE = CF.求证:/ DPA=Z DPC (初二)3、设ABCD 为圆内接凸四边形,求证: AB- CD^AD- BC = AC- BD.(初三)B ---------------------------- C经典难题(五)1、设P是边长为1的正△ ABC内任一点,L = PA + PB + PC ,求证:B C2、已知:P是边长为1的正方形ABCD内的一点,求PA+ PB+ PC的最小值.3、P为正方形ABCD内的一点,并且PA= a, PB= 2a, PC= 3a,求正方形的边长.A D4、如图,△ ABC中,/ ABC=Z ACB= 80°, D E分别是AB AC上的点,/ DCA= 30°, =20°,求/ BED的度数.经典难题解答经典难题(一)1.如下图做GHL AB,连接EO由于GOFE四点共圆,所以/ GFH kZ OEG, 即厶OGE可得■EO=GO=C°,又CO=EO所以CD=G碍证。
平面几何经典难题及解答

1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

平面几何之阿布丰王创作经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .2、已知:如图,P 是正方形ABCD求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 24、已知:如图,在四边形ABCD 中,AD 的中点,AD 、BC 的延长线交MN 求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 直线,交圆于B 、C 及D 、E ,直线EB 及CD 求证:AP =AQ .(初二)3、如果上题把直线MN题:设MN 是圆O 的弦,过MN CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 方形ACDE 和正方形CBFG ,点P 是EF求证:点P 到边AB 的距离等于AB 经典难1、如图,四边形ABCD 为正方形,DE ∥交于F .求证:CE =CF 2、如图,四边形ABCD 交DA 延长线于F .求证:AE =AF 3、设P 是正方形ABCD DCE .求证:PA =PF 4、如图,PC 切圆O 于AF 与直线PO 相交于B 1、已知:△ABC 4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB+PC 的最小值.3、P 为正方形ABCD 内的一点,而且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E的点,∠DCA =300,∠EBA =200,求∠BED APC B P ADCBCBD A F PDE CBAAPC B经典难题解答:经典难题(一)⊥AB,连接EO。
平面几何经典难的题目及解答
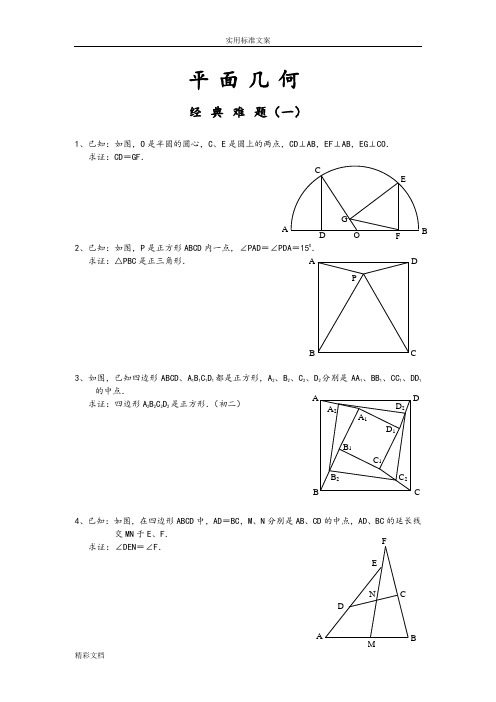
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A PC D B AFG C EBOD D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何难题及解答
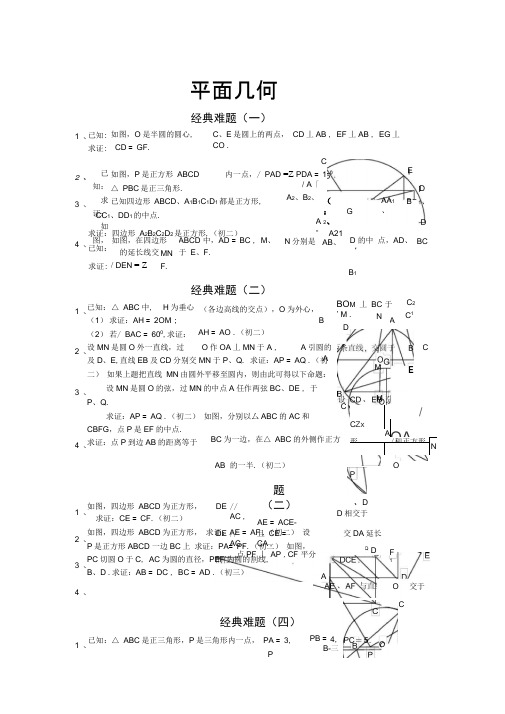
平面几何经典难题(一)已知:求证:已知:求证:如图,如图,O是半圆的圆心,CD = GF.C、E是圆上的两点,CD丄AB , EF丄AB , EG丄CO .如图,P是正方形ABCD△ PBC是正三角形.已知四边形ABCD、A1B1C1D1都是正方形,CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)已知:求证:如图,在四边形的延长线交/ DEN = Z△ ABC 中,ED(;2、AA1、BGA-C内一点,/ PAD =Z PDA = 1/ A「A2、B2、D 的中点,AD、‘MNF.ABCD 中,AD = BC , M、于E、F.N分别是A21AB、B1H为垂心已知:(1)求证:AH = 2OM ;(2)若/ BAC = 600,求证:设MN是圆O外一直线,过经典难题(二)(各边高线的交点),O为外心,BAH = AO .(初二)O作OA丄MN于A ,及D、E,直线EB及CD分别交MN于P、Q. 求证:AP = AQ .(初二)如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE , 于P、Q.求证:AP = AQ .(初二)如图,分别以厶ABC的AC和CBFG,点P是EF的中点.求证:点P到边AB的距离等于BCBO M丄BC 于'M .C2C1N ADCEA引圆的ABC为一边,在△ ABC的外侧作正方/C ZxA OA形/和正方形NAB 的一半.(初二)O题(二)AE = ACE-、DD相交于//AC ,如图,四边形ABCD为正方形,求证:CE = CF.(初二)如图,四边形ABCD为正方形,求证:AE = AF .(初二)设P是正方形ABCD 一边BC上求证:PA= PF.(初二)如图,PC切圆O于C, AC为圆的直径,PEF为圆的割线,B、D .求证:AB = DC , BC = AD .(初三)DEDE //AC ,且CE =CA ,点PF 丄AP , CF 平分经典难题(四)已知:△ ABC是正三角形,P是三角形内一点,PA = 3,PF1A交于OCQ D交DA延长PB =O4,B-三1、2、3、4、1、2、3、4、1、2、3、4、1、3、P 为正方形 ABCD 内的一点,并且 PA = a , PB = 2a , PC = 3a ,求正方形的边长.4、如图,△ ABC 中,/ ABC =Z ACB = 80u, D 、E 分别是 AB 、AC /EBA = 20u ,求/ BED 的度数.经典难题解答:经典难题(一)1•如下图做 GH 丄AB,连接E0。
平面几何经典难题及解答
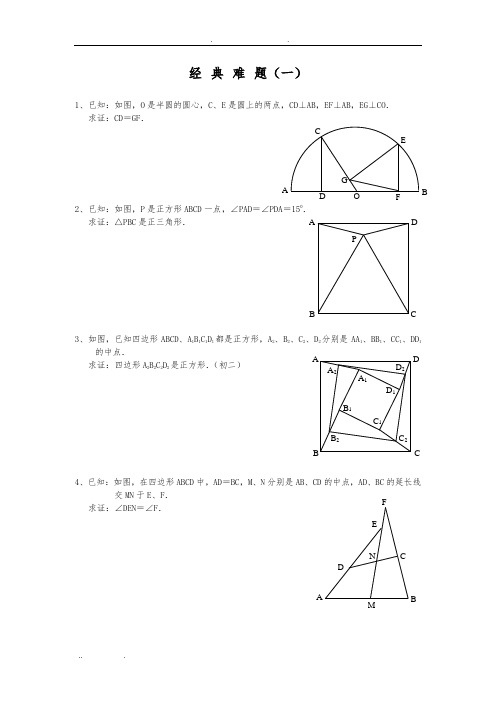
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC DCA =300,∠EBA=200,求∠BED 的度数.经典难题解答:APCBACBPDEDCB A A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答
平面几何经典难题及解答(总5页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF . 2、已知:如图,P 是正方形ABCD 内一点,∠求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC 点,AD 、BC 的延长线交MN 于E 、F求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦分别交MN 于P 、Q . A BF求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 经典难1、如图,四边形ABCD 为正方形,DE ∥AC ,求证:CE =CF 2、如图,四边形ABCD 长线于F .求证:AE =AF 3、设P 是正方形ABCD 求证:PA =PF 4、如图,PC 切圆O 于C ,PO 相交于B 、D .求证:1、已知:△ABC 求:∠APB 2、设P 是平行四边形ABCD 求证:∠PAB =∠PCB3、设ABCD4、平行四边形ABCD 于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数. 经典难题解答:经典难题(一)1.如下图做GH ⊥AB,连接EO 。
平面几何经典难题及解答
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 0,∠EBA =200,求∠BED 的度数.APCBACBPDA CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
(精心整理)平面几何经典难题及解答
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.APCBACBPDA CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何难题及解答
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DAA 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH ⊥AB,连接EO 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典难题(一)
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .
2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.
求证:△PBC 是正三角形.
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、
DD 1的中点.
求证:四边形A 2B 2C 2D 2是正方形.(初二)
4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延
长线交MN 于E 、F .
求证:∠DEN =∠F .
A P
C D B A F
G C E
B
O D D 2 C 2
B 2 A 2
D 1 C 1 B 1
C B D
A
A 1 B
F
1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且
(1)求证:AH =2OM ;
(2)若∠BAC =600,求证:AH =AO .(初二)
2、设MN 是圆O 外一直线,过
O 作OA ⊥MN 于A ,自A D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)
3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:
设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、
Q .
求证:AP =AQ .(初二)
4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,
点P 是EF 的中点.
求证:点P 到边AB 的距离等于AB 的一半.
1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .
求证:CE =CF .(初二)
2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .
求证:AE =AF .(初二)
3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .
求证:PA =PF .(初二)
4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、
D .求证:AB =DC ,BC =AD .(初三)
1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.
求:∠APB 的度数.(初二)
2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)
3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .
4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE
与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)
1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:
≤L<2.
2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.
3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.
4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC
0EBA =200,求∠BED 的度数.。
