冲激响应和卷积分析
阶跃响应、冲激响应和卷积积分

清华大学电机系电路原理教学组第9章阶跃响应、冲激响应和卷积积分的应用9.1 阶跃函数和冲激函数本章重点9.4 电路在任意激励作用下的零状态响应——卷积积分9.5 电容电压和电感电流的跃变9.2 阶跃响应9.3 冲激响应清华大学电机系电路原理教学组•阶跃响应和冲激响应 本章重点•阶跃函数和冲激函数•卷积积分返回目录•电容电压和电感电流的跃变清华大学电机系电路原理教学组9.1 阶跃函数和冲激函数一、单位阶跃函数(unit step function )1. 定义tε(t )10()t ε用可描述开关的动作。
+–u C U S ε(t )RCdef0 (0)() 1 (0)t t t ε<⎧=⎨>⎩def S S 0 (0)() (0)t U t U t ε<⎧=⎨>⎩U SS+–u C R C开关在t =0 时闭合清华大学电机系电路原理教学组2. 延迟的单位阶跃函数tε(t-t 0)t 0def0000 ()() 1 ()t t t t t t ε<⎧−=⎨>⎩3. 由单位阶跃函数可组成复杂的信号U SS+–u C RC开关在t =t 0时闭合清华大学电机系电路原理教学组0()()()f t t t t εε=−−t 0t-ε(t -t 0)ε(t )0f (t )1解所示矩形脉冲可分解为阶跃函数和延迟阶跃函数相加。
例1⎩⎨⎧><<<=), 0( 0)0( 1)(00t t t t t t f 1t 0tf (t )0试用阶跃函数表示上图所示的矩形脉冲。
清华大学电机系电路原理教学组()[()(1)](1)f t t t t t εεε=−−+−11t1t1f (t )例2试用阶跃函数表示图示的波形。
解f (t ) 分成两段表示。
1t101t1+(0< t <1)()[()(1)]f t t t t εε=−−(1< t )()(1)f t t ε=−则清华大学电机系电路原理教学组二、单位冲激函数(unit pulse function )1. 单位脉冲函数1()[()()]p t t t εεΔΔ=−−0lim ()()p t t Δδ→=令1ΔΔ→→∞面积不变Δ1/Δtp (t )0Δ减小,脉冲变窄,面积不变。
阶跃响应冲击响应与卷积积分法

补充第一章 阶跃响应冲击响应与卷积积分法电路中除电阻元件外,还包括有电容和电感等动态元件,如此的电路称为动态电路。
在动态电路分析中,鼓励和响应都表示为时刻t 的函数,采纳微分方程求解电路和分析电路的方式,称为时域分析法。
本章要紧讨论一阶电路的阶跃响应、冲激响应、任意输入的零状态响应,和二阶电路在恒定输入下的零状态响应。
§1-1 阶跃响应和冲激响应电路的输入除恒定不变的常量(即恒定输入或直流输入)和按正弦规律变更的交流量(即正弦输入)之外,常见的还有另外两种奇异函数,即阶跃函数和冲激函数。
本节就来讨论这两种函数的概念、性质及作用于线性动态电路时所引发的响应。
单位阶跃函数(unit step function )用()t ε来表示,它概念为 0(0)()1(0)t t t ε<⎧=⎨>⎩ 波形如图1-1(a )所示,在0t =处,()t ε由0跃变至1。
若是单位阶跃函数的跃变点不是在0t =处,而是在0t t =处,波形如图1-1(b )所示,那么称它为延迟的单位阶跃函数,用0()t t ε-表示,即0000()()1()t t t t t t ε<⎧-=⎨>⎩图1-1单位阶跃函数与任一常量K 的乘积()K t ε仍是一个阶跃函数,现在阶跃的幅度为K 。
单位阶跃函数与任一函数()f t 的乘积将只保留该函数在阶跃点以后的值,而使阶跃点以前的值变成零,即有0000(0)()()()(0)0()()()()()t f t t f t t t t f t t t f t t t εε<⎧=⎨>⎩<⎧-=⎨>⎩因此,单位阶跃函数能够用来“起始”一个任意函数()f t ,这给函数的表示带来了方便。
例如关于线性函数()(f t Kt K =为常数),由图1-2(a)、(b)、(c)能够清楚地看出()f t 、()()f t t ε及0()()f t t t ε-的不同。
说明系统零状态响应、冲激响应、阶跃响应的定义及三者之间的联系

说明系统零状态响应、冲激响应、阶跃响应的定义及三者之间的联系:
1.零状态响应:
零状态响应是系统在没有初始储能(即系统处于零状态)下,由外部激励引起的系统响应。
它可以通过系统的传递函数或冲激响应来描述。
在零状态响应中,系统的储能不随时间变化,只与外部激励有关。
2.冲激响应:
冲激响应是系统在单位冲激函数激励下的响应,它是系统的传递函数的冲激函数形式。
冲激响应描述了系统对单位冲激函数的响应,可以看作是时间域上的积分运算的结果。
冲激响应是系统固有的特性,与外部激励无关。
3.阶跃响应:
阶跃响应是系统在单位阶跃函数激励下的响应。
阶跃响应描述了系统在阶跃信号作用下随时间变化的动态过程,包括上升、稳定和下降等阶段。
阶跃响应可以通过系统的传递函数或冲激响应来求解。
三者之间的联系:
零状态响应、冲激响应和阶跃响应之间存在密切的联系。
对于线性时不变系统,零状态响应可以通过冲激响应和阶跃响应来描述。
具体来说,系统的零状态响应等于冲激响应和阶跃响应的卷积,即y(t)=h(t)*u(t),其中y(t)表示零状态响应,h(t)表示冲激响应,u(t)表示阶跃响应。
这个公式表明,系统的零状态响应可以通过冲激响应和阶跃响应的卷积运算来获得。
冲击响应

系统并联
f1 (t ) [ f 2 (t ) f3 (t )] f1 (t ) f 2 (t ) f1 (t ) f 3 (t )
系统并联,框图表示:
h(t )
f (t )
f (t ) f (t )
h1 (t )
f (t ) * h1 (t )
g (t )
f (t ) h1 (t ) f (t ) h2 (t )
可表示为:
e(t ) e(t ) (t )
三.利用卷积求系统的零状态响应
当一个信号作用于系统时,响应为
e( ) (t ) d r (t ) H e(t ) H e( ) H (t ) d 当系统为线性时
3. i ( t ) e( ) h(t ) d
e
1 2
i (t )
L 1H
u( ) u( 2) e ( t ) u(t ) d
e t e 2 u( )u( t )d e t e 2 u( 2)u( t )d
卷积积分中积分限的确定是非常关键的。
四.卷积的计算
已知e( t ) e
u(t ) u(t 2),求i(t )的零状态响应。 R 1 d i t 1.列写KVL方程 L Ri t et
t 2
2.冲激响应为
dt h( t ) e t u( t )
u (t )
H
g (t )
系统的输入 e t u t ,其响应为 r t gt 。系统方程的 右端将包含阶跃函数 ut ,t>0时输入不为0,所以其响应除 了齐次解外,还有特解项。
§2.2++冲激响应和阶跃响应及卷积(1)

对t>0时,有 时
h”(t) + 6h’(t) + 5h(t) = 0
微分方程的特征根为– , 微分方程的特征根为 2, – 3。故系统的冲激响应为 。 h(t)= C1e–2t + C2e–3t , t>0 代入初始条件 h(0+) = – 3, h’(0+) =12 , 求得C , 求得 1=3,C2= – 6, 所以 h(t)= 3e–2t – 6e–3t , t > 0 结合式(2)得 结合式 得 h(t)= δ(t) + (3e–2t – 6e–3t)ε(t)
lim
∆→0
∞
ˆ f (t) = f (t ) = ∫
∞ −∞
f (τ )δ (t −τ ) d τ
第 任意信号作用下的零状态响应
f (t) 根据h(t)的定义: 的定义: 根据 的定义 由时不变性: 由时不变性:
∞
LTI系统 LTI系统 零状态
yzs(t) h(t) h(t -τ) f (τ) h(t -τ)
3 .卷积积分的定义 卷积积分的定义
已知定义在区间( 已知定义在区间( – ∞,∞)上的两个函数 1(t) , )上的两个函数f 和f2(t),则定义积分 ,
∞
f (t) = ∫ f1 (τ ) f 2 (t −τ )dτ
−∞
为f1(t)与f2(t)的卷积积分,简称卷积;记为 卷积; 与 的卷积积分,简称卷积 f(t)= f1(t)*f2(t) 注意:积分是在虚设的变量τ下进行的 为积分变量 下进行的, 为积分变量, 注意:积分是在虚设的变量 下进行的,τ为积分变量, t为参变量。结果仍为 的函数。 为参变量。 为参变量 结果仍为t 的函数。
卷积算法实验报告程序

一、实验目的通过本次实验,加深对卷积算法的理解,掌握离散时间系统中的卷积运算方法,并学会使用MATLAB进行卷积运算的仿真。
二、实验原理卷积是一种线性时不变(LTI)系统的数学运算,用于描述系统输入信号与系统冲激响应的卷积结果。
在离散时间系统中,卷积运算可以表示为:\[ y[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k] \]其中,\( y[n] \) 是系统的输出信号,\( x[k] \) 是系统的输入信号,\( h[n] \) 是系统的冲激响应,\( n \) 是时间变量。
MATLAB提供了`conv`函数来进行卷积运算,其语法为:\[ y = conv(x, h) \]其中,\( x \) 和 \( h \) 分别是输入信号和冲激响应的向量。
三、实验内容1. 创建输入信号和冲激响应使用MATLAB创建一个简单的输入信号 \( x[n] \) 和一个冲激响应 \( h[n] \)。
```matlab% 创建输入信号 x[n] = cos(2pi0.5n)n = 0:100;x = cos(2pi0.5n);% 创建冲激响应 h[n] = u[n] - u[n-10]h = [ones(1,10), zeros(1,90)];```2. 进行卷积运算使用`conv`函数进行卷积运算,并绘制输入信号、冲激响应和输出信号的图形。
```matlab% 进行卷积运算y = conv(x, h);% 绘制图形figure;subplot(3,1,1);stem(n, x);title('输入信号 x[n]');subplot(3,1,2);stem(n, h);title('冲激响应 h[n]');subplot(3,1,3);stem(n, y);title('输出信号 y[n]');```3. 分析卷积结果分析卷积结果,观察输出信号的特性,并与理论预期进行对比。
系统的零状态响应=激励与系统冲激响应的卷积
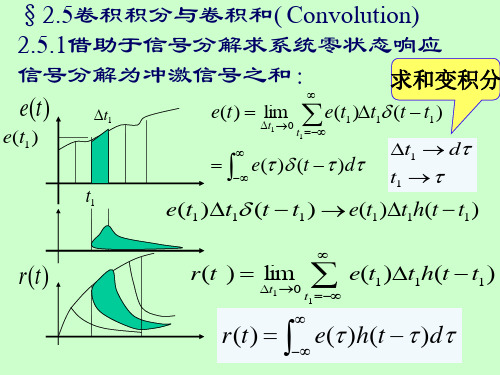
2.5.1借助于信号分解求系统零状态响应
信号分解为冲激信号之和:
求和变积分
e(t) t1
e(t1 )
t1
e(t)
lim
t1 0
e(t1 )t1
t1
(t
t1 )
e( ) (t )d
t1 d t1
e(t1)t1 (t t1) e(t1)t1h(t t1)
f (t)
f1(1) (t) *
f2(1) (t)
d dt
f1 t *
t
f 2 ( )d
三、与冲激函数或阶跃函数的卷积
(1)与冲激函数卷积
1. f (t) * (t) (t) * f (t) ( ) f (t )d f (t)
某函数与冲激函数的卷积是其本身
2. f (t) * (t t0) (t t0) * f (t)
t
t
f1() * f2 ()d f1() * f2 ()d
t
f2 () * f1()d
类似地:对高阶导数和积分
f (t) f1(t) * f2(t)
则:
f
(i ) (t)
f1( j) (t) *
f
(i 2
j
)
(t)
其中,I,j取正整数时,为导数阶次 若I,j取负整数时,为重积分次数,如
r(t)
r(t
) lim t10 t1
e(t1)t1h(t t1)
r(t) e( )h(t )d
e(t)
lim
t1 0
e(t1)t1
t1
(t
t1)
卷积的物理含义图解:
k (t t1)
卷积的本质及物理意义(整理)

[衰减系数是(t-τ)的函数,仔细品味]
数学表达为:y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事,太残忍了。除了人以外,其他事物也符合这条规律吗?
——呵呵,县令大人毕竟仁慈。其实除人之外,很多事情也遵循此道。好好想一想,铁丝为什么弯曲一次不折,快速弯曲多次却会轻易折掉呢?
卷积是在时域求解LTI系统对任意激励的零状态响应的好方法,可以避免直接求解复杂的微分方程。
从数学上来说卷积就是定义两个函数的一种乘法。对离散序列来说就是两个多项式的乘法。物理意义就是冲激响应的线性叠加,所谓冲激响应可以看作是一个函数,另一个函数按冲激信号正交展开。
在现实中,卷积代表的是将一种信号搬移到另一频率中.比如调制.这是频率卷
把一个点的像素值用它周围的点的像素值的加权平均代替。
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
卷积的物理意义,解释的真幽默!
有一个七品县令,喜欢用打板子来惩戒那些市井无赖,而且有个惯例:如果没犯大罪,只打一板,释放回家,以示爱民如子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验2离散系统的差分方程、冲激响应和卷积分析
一、实验目的
1 加深对离散系统的差分方程、冲激响应和卷积分析方法的理解。
二、实验原理
离散系统
其输入、输出关系可用以下差分方程描述:
∑=∑=-=-M k k N k k k n x p k n y d 00][][ 输入信号分解为冲激信号:∑-=∞-∞
=m m n m x n x ][][][δ
记系统单位冲激响应 : ][][n h n →δ
则系统响应为如下的卷积计算式: ∑∞-∞=-=
*=m m n h m x n h n x n y ][][][][][ 当N k d k ,...2,1,0==时,h[n]是有限长度的(n :[0,M]),称系统为FIR 系统;反之,称系统为IIR 系统。
在MATLAB 中,可以用函数y=Filter(p,d,x) 求解差分方程,也可以用函数
y=Conv(x,h)计算卷积。
二、实验内容
编制程序求解下列两个系统的单位冲激响应和阶跃响应,并绘出其图形。
(1): y [n ]+0.75y [n -1]+0.125y [n -2]=x [n ]-x [n -1]
(2): y [n ]=0.25{x [n -1]+x [n -2]+x [n -3]+x [n -4]+x [n -5]}
程序(1):
A=[1,0.75,0.125];
B=[1,-1];
x1=[1,zeros(1,10)];
x2=ones(1,20);
y1=filter(B,A,x1);
subplot(2,2,1);
stem(y1);
title('y1单位冲击响应')
y2=filter(B,A,x2);
subplot(2,2,2);
stem(y2);
title('y2阶跃响应');
y3=conv(x1,y1);
subplot(2,2,3);
stem(y3);
title('y3卷积');
y4=conv(x2,y1);
subplot(2,2,4);
stem(y4);
title('y4卷积')
程序(1)图
程序(2):
A=[1];
B=[0,0.25,0.25,0.25,0.25];
x1=[1,zeros(1,10)];
x2=ones(1,20);
y1=filter(B,A,x1);
subplot(2,2,1);
stem(y1);
title('y1单位冲击响应')
y2=filter(B,A,x2);
subplot(2,2,2);
stem(y2);
title('y2阶跃响应');
y3=conv(x1,y1);
subplot(2,2,3);
stem(y3);
title('y3卷积');
y4=conv(x2,y1);
subplot(2,2,4);
stem(y4);
title('y4卷积')
程序(2)图
三、理论计算:
经计算:
系统(1): y[n]+0.75y[n-1]+0.125y[n-2]=x[n]-x[n-1]
理论冲激响应为:因为y[n]为因果函数,由递归计算所得:
X[n]= δ(n)
当n<0时,h(n)=0
h(0)=1, h(1)=-7/4, h(2)=19/16, h(3)=-43/64 ..... ......
h(z)=7.5*(-0.5).^n*u(n)- (-0.25).^n*u(n)
理论阶跃响应为:因为y[n]为因果函数,由递归计算所得:
X[n]=u(n)
当n<0时,g(n)=0
g(0)=1, g(1)=-3/4, g(2)=7/16, g(3)=-9/64......
.......
g(z)=1.5*(-0.5).^n-(-0.25).^n
系统(2):y[n]=0.25{x[n-1]+x[n-2]+x[n-3]+x[n-4]+x[n-5]}
同理,由递归方法可得:
理论冲激响应为:h(z)=0.25*[δ(n-1)+ δ(n-2)+ δ(n-3)+ δ(n-4]
理论阶跃响应为:g(z)=0.25*[u(n-1)+ u(n-2)+ u(n-3)+ u(n-4)]
将n值分别代入理论式h(z)和g(z),将结果与程序结果图比较可知理论与程序结果一致。
四、实验小结
通过这次实验,基本学会了用MATLAB软件编程求离散系统的单位脉冲响应和单位冲击响应,对解离散系统差分方程有了进一步学习。
