理想流体流动(1)
合集下载
1理想流体 稳定流动
龙 卷 风
缓慢的水流
2-1理想流体 稳定流动
第二章流体的运动
二、稳定流动（steady flow）（定常流动）
1.稳定流动 一般流动：v（x、y、z、t） 稳定流动： v （ x、y、z） 2.流线(streamline) 在流场中画出的一些曲线, 曲线上的任意一点的切线 方向 , 与流过该点流体质 元的速度方向一致.
连续介质 将流体看作是大量的宏观小、微观大的流体质 元组成并研究其宏观行为 ,因此可忽略物体微 观结构的量子性,这种物质模型就是连续介质.
2-1理想流体 稳定流动
第二章流体的运动
流体运动的描述方法
统计公交车的客运量时,可采用两种方法: (1)在每辆公交车上设统计员,统计其在不同时 刻(站点)上下车的人数,称为随体法.
2-1理想流体 稳定流动
第二章流体的运动
ቤተ መጻሕፍቲ ባይዱ
注意：稳定流动的流线 （1）流线不能相交
流体流过不同形状障碍物的流线
（2）流线是不随时间而
变化的曲线
（3）流线与流体粒子的 运动轨迹重合
2-1理想流体 稳定流动
第二章流体的运动
3.流管（
(stream tube)
------由流线围成的管子。（假想的管子）
2-1理想流体 稳定流动
第二章流体的运动
第二章
2 - 0
2 - 1 2 - 2 2 - 3 2 – 4
流体的运动
稳定流动
简介
理想流体
伯努利方程 粘性流体的流动 粘性流体的运动规律
2 - 5
血液在循环系统中的流动
2-1理想流体 稳定流动
物态
第二章流体的运动
物体根据存在的形态分为固态、液态和气态.
缓慢的水流
2-1理想流体 稳定流动
第二章流体的运动
二、稳定流动（steady flow）（定常流动）
1.稳定流动 一般流动：v（x、y、z、t） 稳定流动： v （ x、y、z） 2.流线(streamline) 在流场中画出的一些曲线, 曲线上的任意一点的切线 方向 , 与流过该点流体质 元的速度方向一致.
连续介质 将流体看作是大量的宏观小、微观大的流体质 元组成并研究其宏观行为 ,因此可忽略物体微 观结构的量子性,这种物质模型就是连续介质.
2-1理想流体 稳定流动
第二章流体的运动
流体运动的描述方法
统计公交车的客运量时,可采用两种方法: (1)在每辆公交车上设统计员,统计其在不同时 刻(站点)上下车的人数,称为随体法.
2-1理想流体 稳定流动
第二章流体的运动
ቤተ መጻሕፍቲ ባይዱ
注意：稳定流动的流线 （1）流线不能相交
流体流过不同形状障碍物的流线
（2）流线是不随时间而
变化的曲线
（3）流线与流体粒子的 运动轨迹重合
2-1理想流体 稳定流动
第二章流体的运动
3.流管（
(stream tube)
------由流线围成的管子。（假想的管子）
2-1理想流体 稳定流动
第二章流体的运动
第二章
2 - 0
2 - 1 2 - 2 2 - 3 2 – 4
流体的运动
稳定流动
简介
理想流体
伯努利方程 粘性流体的流动 粘性流体的运动规律
2 - 5
血液在循环系统中的流动
2-1理想流体 稳定流动
物态
第二章流体的运动
物体根据存在的形态分为固态、液态和气态.
第二章 理想流动与非理想流动1
第二章
理想流动与非理想 流动反应器
流体在反应器中的流动情况影响着反应速率、反应选择率， 直接影响反应结果，研究反应器的流动模型是反应器选型、设计 和优化的基础。 流动模型可以抽象出两种极限的情况：一种是完全没有返混 的活塞流反应器；另一种是返混达到极大值的全混流反应器。 实际生产中的多数管式反应器及固定床催化反应器等可作活 塞流反应器处理，多数槽式反应器可作全混流反应器处理。
对活塞流反应器，物料质点是平推着向前流动的，物料质点在反 应器中的逗留时间相同不产生返混。而在全混流反应器中，不同 年龄的质点达到完全混合，有的逗留时间很短，有的却很长，返 混程度最大。 活塞流与全混流是两种理想流型：前者理想置换，没有返混；后 者理想混合，返混最大。而介于两者之间的流型，是非理想流型， 存在着不同程度的返混现象。
2 全混流模型 亦称理想混合模型或连续搅拌槽式反应器模型，如图2-1（c）所 示，是一种返混程度为无穷大的理想化流动模型。
全混流假定反应物料以稳定流率流入反应器，在反应器中，刚进 入反应器的新鲜物料与存留在器内的物料在瞬间达到完全混合。 反应器中所有空间位置的物料参数都是均匀的，等于反应器出口 处的物料性质，即反应器内物料温度、浓度均匀，与出口处物料 温度、浓度相等。而物料质点在反应器中的逗留时间参差不齐， 有的很短，有的很长，形成一个逗留时间分布。 搅拌十分强烈的连续搅拌槽式反应器中的流体流动可视为全混流。
（2）热量衡算 热量衡算以能量守恒与转化定律为基础，在计算反应速率时必须 考虑反应物系的温度，通过热量衡算可以计算反应器中温度的变 化。与物料衡算相仿，对反应器或其一微元体积进行反应物料的 热量衡算，基本式为 （带入的热焓）＝（流出的热焓）十（反应热）十（热量的 累积）十（传向环境的热量） （2-2） 式中反应热项，放热反应时为负值，吸热反应时为正值。
理想流动与非理想 流动反应器
流体在反应器中的流动情况影响着反应速率、反应选择率， 直接影响反应结果，研究反应器的流动模型是反应器选型、设计 和优化的基础。 流动模型可以抽象出两种极限的情况：一种是完全没有返混 的活塞流反应器；另一种是返混达到极大值的全混流反应器。 实际生产中的多数管式反应器及固定床催化反应器等可作活 塞流反应器处理，多数槽式反应器可作全混流反应器处理。
对活塞流反应器，物料质点是平推着向前流动的，物料质点在反 应器中的逗留时间相同不产生返混。而在全混流反应器中，不同 年龄的质点达到完全混合，有的逗留时间很短，有的却很长，返 混程度最大。 活塞流与全混流是两种理想流型：前者理想置换，没有返混；后 者理想混合，返混最大。而介于两者之间的流型，是非理想流型， 存在着不同程度的返混现象。
2 全混流模型 亦称理想混合模型或连续搅拌槽式反应器模型，如图2-1（c）所 示，是一种返混程度为无穷大的理想化流动模型。
全混流假定反应物料以稳定流率流入反应器，在反应器中，刚进 入反应器的新鲜物料与存留在器内的物料在瞬间达到完全混合。 反应器中所有空间位置的物料参数都是均匀的，等于反应器出口 处的物料性质，即反应器内物料温度、浓度均匀，与出口处物料 温度、浓度相等。而物料质点在反应器中的逗留时间参差不齐， 有的很短，有的很长，形成一个逗留时间分布。 搅拌十分强烈的连续搅拌槽式反应器中的流体流动可视为全混流。
（2）热量衡算 热量衡算以能量守恒与转化定律为基础，在计算反应速率时必须 考虑反应物系的温度，通过热量衡算可以计算反应器中温度的变 化。与物料衡算相仿，对反应器或其一微元体积进行反应物料的 热量衡算，基本式为 （带入的热焓）＝（流出的热焓）十（反应热）十（热量的 累积）十（传向环境的热量） （2-2） 式中反应热项，放热反应时为负值，吸热反应时为正值。
理想流体的流动
（1）适用于理想流体的定常流动。
（2）对实际流体，只要其黏滞性很小，就可应用伯努利方程。 如空气、水和酒精。
（3）伯努利方程广泛应用于水利、造船、化工、航天等领域。
三、伯努利方程的应用
（1）等高流线中流速与压强的关系
P 1 v2 C
2
Sv qV 常量 C
当S较小时，v 较大，P较小。
由 S1v1 =S2v2
得 v2 = 4v1 = 4 m•s-1
又由
p1
1 2
v12
p2
1 2
v22
得
p1
p2
1 2
v22
v12
1 1.0103 42 12 7.5103 Pa 2
粗管内的压强高于细管
例 水从图示的水平管道1中流入，并通过支管2和3流入管4。
如管1中的流量为900cm3•s-1. 管1、2、3的截面积均为15cm2,
管4的截面积为10cm2,假设水在管内作稳恒流动，
求 （1）管2、3、4的流量; （2）管2、3、4的流速;
（3）管1、4中的压强差.
2
v2
1
v1
4
v4
3
v3
解 (1)由连续性原理知 Q4= Q1 = 900cm3•s-1 ∵ S2 = S3 Q2 + Q3 = Q1 ∴ Q2 = Q3 = 450cm3•s-1
v2
所以流线不会相交。
流速大
流线密处，表示流速大。
四、流管（flow tube） 流管：由一组流线围成的管状区域称为流管。
流管内、外的流体都不会穿越管壁。
通常所取的“流管”都是“细流管”。 细流管的截面积S 0 ，就称为流线。 作定常流动的液体可以视为由无数稳定的细流管组成，所以， 任一流管中的流动可以代表整个流体的流动。
（2）对实际流体，只要其黏滞性很小，就可应用伯努利方程。 如空气、水和酒精。
（3）伯努利方程广泛应用于水利、造船、化工、航天等领域。
三、伯努利方程的应用
（1）等高流线中流速与压强的关系
P 1 v2 C
2
Sv qV 常量 C
当S较小时，v 较大，P较小。
由 S1v1 =S2v2
得 v2 = 4v1 = 4 m•s-1
又由
p1
1 2
v12
p2
1 2
v22
得
p1
p2
1 2
v22
v12
1 1.0103 42 12 7.5103 Pa 2
粗管内的压强高于细管
例 水从图示的水平管道1中流入，并通过支管2和3流入管4。
如管1中的流量为900cm3•s-1. 管1、2、3的截面积均为15cm2,
管4的截面积为10cm2,假设水在管内作稳恒流动，
求 （1）管2、3、4的流量; （2）管2、3、4的流速;
（3）管1、4中的压强差.
2
v2
1
v1
4
v4
3
v3
解 (1)由连续性原理知 Q4= Q1 = 900cm3•s-1 ∵ S2 = S3 Q2 + Q3 = Q1 ∴ Q2 = Q3 = 450cm3•s-1
v2
所以流线不会相交。
流速大
流线密处，表示流速大。
四、流管（flow tube） 流管：由一组流线围成的管状区域称为流管。
流管内、外的流体都不会穿越管壁。
通常所取的“流管”都是“细流管”。 细流管的截面积S 0 ，就称为流线。 作定常流动的液体可以视为由无数稳定的细流管组成，所以， 任一流管中的流动可以代表整个流体的流动。
化工原理第一章 流体流动1
pB pa 0 gR
A
B
所以
下午6时51分
0 h R
8喻国华
3. 液封高度的计算
液封作用： 确保设备安全：当设备 内压力超过规定值时，气 体从液封管排出； 防止气柜内气体泄漏。 液封高度：
p(表) h g
9喻国华
下午6时51分
管内流体流动基本方程式
流量与流速
稳定流动与不稳定流动 稳定流动系统的质量守恒 ——连续性方程 稳定流动流动系统的能量守恒 ——柏努利方程
p1 p2 pa Hg g ( z0 z2 ) p4 p3 p1 H2O g ( z4 z2 ) p6 p5 p4 Hg g ( z4 z6 ) p p6 H2O g ( z7 z6 )
p pa H 2O g z6 z2 z7 z4 H g g ( z0 z 4 z 2 z 6 ) 1000 9.81 (0.7 0.9 2.5 2.0) 13600 9.81 (2.0 2.1 0.9 0.7) 下午6时51分 305.91kPa
p ——静压头 g
He——外加压头或有效压头。
Σhf——压头损失
下午6时51分
26喻国华
（3）以单位体积流体为基准 将(1)式各项同乘以 :
z1g z1g 1 1 u12 p1 We z2 g u2 2 p2 W f 2 2 1 1 u12 p1 We z2 g u2 2 p2 p f 2 2
6喻国华
2. 液位测量
（1）近距离液位测量装置
压差计读数R反映出容器
内的液面高度。
0 h R
液面越高，h越小，压差计读数R越小；当液 面达到最高时，h为零，R亦为零。
A
B
所以
下午6时51分
0 h R
8喻国华
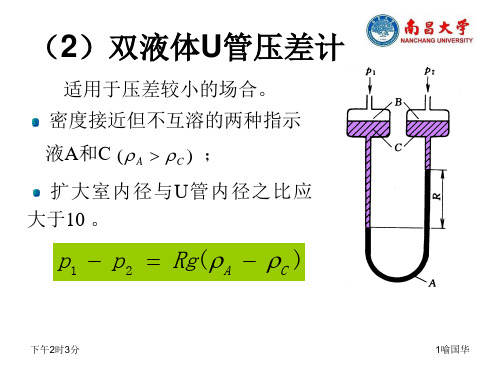
3. 液封高度的计算
液封作用： 确保设备安全：当设备 内压力超过规定值时，气 体从液封管排出； 防止气柜内气体泄漏。 液封高度：
p(表) h g
9喻国华
下午6时51分
管内流体流动基本方程式
流量与流速
稳定流动与不稳定流动 稳定流动系统的质量守恒 ——连续性方程 稳定流动流动系统的能量守恒 ——柏努利方程
p1 p2 pa Hg g ( z0 z2 ) p4 p3 p1 H2O g ( z4 z2 ) p6 p5 p4 Hg g ( z4 z6 ) p p6 H2O g ( z7 z6 )
p pa H 2O g z6 z2 z7 z4 H g g ( z0 z 4 z 2 z 6 ) 1000 9.81 (0.7 0.9 2.5 2.0) 13600 9.81 (2.0 2.1 0.9 0.7) 下午6时51分 305.91kPa
p ——静压头 g
He——外加压头或有效压头。
Σhf——压头损失
下午6时51分
26喻国华
（3）以单位体积流体为基准 将(1)式各项同乘以 :
z1g z1g 1 1 u12 p1 We z2 g u2 2 p2 W f 2 2 1 1 u12 p1 We z2 g u2 2 p2 p f 2 2
6喻国华
2. 液位测量
（1）近距离液位测量装置
压差计读数R反映出容器
内的液面高度。
0 h R
液面越高，h越小，压差计读数R越小；当液 面达到最高时，h为零，R亦为零。
第一节 理想流体与稳定流动
（2）流管 在流体内某点附近取垂直于流线的面元，则通 过该面元边界的流线围成一细管，称为流管。
流线
流管
性质：流管内、外的流体都不会穿过流管壁。
（3）稳定流动
流动的流体中每一点的流速矢量 v 构成一个流速场。
流体流经的空间称为流体空间或流场 。
一般，空间各点的流速随时间变化：
vv(x、y、来自、t)称为流体的不定常流动。
特殊情况下，流速不随时间变化：
v
v(
x、y、z
)
称为流体的稳定流动，或定常流动。
v1 v2 v3
问：定常流动时，流线与流迹是否重合？
是
特点：流线和流管均保持固定的形状和位置
流体质量元在不同地点的速度可以各不相同。 流体在空间各点的速度分布不变。 “定常流动”并不仅限于“理想流体”。
（一）理想流体与稳定流动
1、 实际流体具有压缩性和黏滞性： （1）压缩性
液体：压缩性极小
气体：压缩性大，但流动性强，所以气体 分子迅速趋于均匀
（2）黏滞性
所谓黏滞性，就是当流体运动时，层与层之间有阻碍相对运 动的内摩擦力。
2、 理想流体
完全不可压缩的无粘滞流体称为理想流体。
3、几个概念
（1）流线
流迹
1 S1v1 2 S2v2 或 Sv C （常量）
此即连续性原理或质量守恒方程，其中 Sv 称为质量流量 Qm 。
对于不可压缩流体， 为常量，故有
Sv QV 常量
上式称为不可压缩流体的连续性原理或体积连续性 方程，其中QV 称为体积流量。
对同一流管而言，截面积 S 小处则速度大， 截面积 S 大处则速度小
流体的连 续性原理
ρvds：质量流量——单位时间内流过流管任一横截面的
中山大学化工原理课件 第1章-流体流动(1)
1 atm(标准大气压)＝1.013×105 Pa ＝760 mmHg ＝10.33 mH2O
绝对压力 ---以绝对真空为基准
（2）压力大小的两种表征方法
表压 ---以当地大气压为基准
表压＝绝对压力－当地大气压
真空度＝当地大气压－绝对压力
真空度=当地大气压-系统绝压 ＝－（系统绝压－当地大气压） ＝－表压 例如某系统真空度为 200mmHg，当地大气压为 101.3kPa， 则：表压＝－真空度＝-200/760*101.3=-26.7kPa 系统绝压=表压＋当地大气压
四. 流体的流动属性 1．流量和流速 体积流量 流量 qV＝ V t
m3 / s
kg/s
qm ＝ qV
m 质量流量 qm ＝ t
流速
qV …… 平均流速 u ＝ A 体积流速 质量流速 qm w＝ A kg/(m2s)
m/s w＝u
qm ＝w A ＝ u A
2．流体的运动状态 (1) 稳定流动 流体流动过程中，任一截面上与流动相 关的物理量 (流速、压强、密度等) 不随时 间变化的流动。 (2) 不稳定流动 在流动过程中，流体在任一截面上的物 理量随时间而变化的流动。
1 7
第二节. 连续性方程式 流体流动过程中 质量守恒 涉及三大守恒定律： 动量守恒 能量守恒
1
质量衡算
衡算范围—划定体积/控制体积/控制体
控制体 2 1
对于在控制体内作稳定流动的流体， 根据质量守恒定律有： qm1 ＝ qm2 ＝ 常数
1 u1 A1 ＝ 2 u2 A2 ＝常数
2
连续性方程式
2 总能量衡算式：U1 + g1Z1 + u1 / 2 + p1/ 1 + Qe +We ＝U2 + g2Z2 + u22/ 2 + p2/ 2 (J/kg)
化工原理第一章 流体流动1
机械能：位能、动能、静压能及外功，可用于输 送流体； 内能与热：不能直接转变为输送流体的能量。
下午6时51分 23喻国华
2．实际流体的机械能衡算 (1) 以单位质量流体为基准 假设 流体不可压缩， 则 1 2
流动系统无热交换，则 qe 0
流体温度不变， 则 U1 U 2 并且实际流体流动时有能量损失。 设1kg流体损失的能量为Σ Wf（J/kg），有：
下午6时51分 2喻国华
例: 如附图所示，水在水平管道内流动。为测量流体 在某截面处的压力，直接在该处连接一U形压差计， 指示液为水银，读数 R ＝ 250mm ， h ＝ 900mm 。
已知当地大气压为101.3kPa，
水 的 密 度 1000kg/m3 ， 水 银 的
密度13600kg/m3 。试计算该截
u2 d1 0.656 u1 d 2
u2=0.656×1.747=1.146m/s
2
由连续性方程,对管１和管２有
9 103 u1 1.747m / s 2 2 0.785 0.081 d1 4 Vs
1
2
3a
对管1和管3有
下午6时51分
u3 d1 2.62 u1 d3
不可压缩性流体， Const.
Vs u1 A1 u2 A2 uA 常数
圆形管道 ： u 1
A2 d 2 u2 A1 d 1
2
即不可压缩流体在管路中任意截面的流速与 管内径的平方成反比 。
下午6时51分
17喻国华
例:如附图所示，管路由一段φ 89×4mm的管1、一 段φ 108×4mm的管2和两段φ 57×3.5mm的分支管
流体力学1答案
考试试卷（A B 卷） 学年第二学期课程名称： 流体力学 一、判断题（20分） 1. 流体质点是指宏观上足够小，而微观上又足够大的流体微团。
（T ） 2. 液体的粘性随温度的升高而增大。
（F ） 3. 气体的粘性随温度的升高而减小。
（F ） 4. 牛顿流体的粘性切应力与速度梯度，即角变形速率成正比。
（T ） 5. 静止的流体只能承受压应力。
（T ） 6. 在描述流体运动中欧拉法没有直接给出流体质点的运动轨迹。
（T ） 7. 定常流动，流线与迹线重合。
（T ） 8. 应用总流伯努利方程解题时，两个断面间一定是缓变流，方程才成立。
（F ） 9. 由于流体粘性的存在和影响，使流体呈现两种不同的流态，就是层流和紊流。
（T ） 10. 雷诺数是表征重力与惯性力的比值。
（F ） 11. 静止的流体中任意一点的各个方向的压强值均相等。
（T ） 12. 静止液体的等压面一定是一个水平面。
（T ） 13. 大气层中的压强与密度、温度的变化有关而且受季节、气候等因素的影响。
（T ） 14. 压力体的体积表示一个数学积分，与压力体内是否有气体无关。
（T ） 15. 理想流体的运动可分为有旋流动和无旋流动两种类型。
（T ） 16. 不可压缩流体的无旋流动由于存在速度势和流函数，故又称为位势流动。
（T ） 17. 如果流场中若干流体微团无绕自身轴线旋转运动，刚称为无旋流动。
（F ） 18. 如果任一条封闭曲线上的速度环量皆为零，则此区域内的流动必为无旋流动。
（T ） 19. 不可压缩流体中的，速度势函数满足拉普拉斯方程，速度势函数是调和函数。
（T ） 20. 在位势流场中，任意曲线上的速度环量等于曲线两端点上速度势函数值之差，而与曲线形状无关。
（T ） 二、填空题（20分） 1. 液体的动力粘性系数随温度的 升高而减小，牛顿流体是指切应力与 速度梯度 成 正比 的流体。
2. 欧拉法中，流体的加速度包括 时变加速度 和 位变加速度 两种，如果流场中时变加速度为零，则称流动为 定常流动 ，否则，流动称为 非定常流动 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
vx ( vx ) ( dx)(vx dx)dydz [ vx dx]dydz x x x
第一节 微分形式的连续方程
C
G F
vx dydz
B
( vx ) [ vx dx]dydz x
H
dy
vy
y
D
z
A
x
vz dx vx
dz
E
单位时间内x方向净质量流量
常见的正压流体
1）等温（T＝T1）流动中的可压缩流体;
2）绝热流动中的可压缩流体;
对于不可压缩流体，
pF
p
第四节 欧拉积分式和伯努利积分式
在以上三个前提条件下,兰姆运动微分 方程可简化为:
第四节 欧拉积分式和伯努利积分式
一、欧拉积分
在无旋流动中 x y z 0
欧拉积分式
第二节 有旋运动与无旋运动
流体微团的旋转角速度不等于零的流 动称为有旋流动；
0
流体微团的旋转角速度等于零的流动 称为无旋流动。
0
即:
第二节 有旋运动与无旋运动
注意:
有旋流动和无旋流动仅由流体微团本身 是否发生旋转来决定，而与流体微团本 身的运动轨迹无关。
第三节 理想流体的运动微分方程
2. 作用在流体上的质量力是有势的
3. 流体不可压缩或为正压流体
第四节 欧拉积分式和伯努利积分式
正压流体
如果流体的密度仅与压强有关，即ρ=ρ(p) ，则 这种流场称为正压性的，流体称为正压流体。这时 存在着一个压强函数pF(x,y,z,t)
dp pF ( p)
第四节 欧拉积分式和伯努利积分式
连续方程：
( v) 0 t
第一节 微分形式的连续方程
用欧拉法分析流体运动时:
d vx vy vz dt t x y z
当地导数 迁移导数
( vx ) ( v y ) ( vz ) 0 展开并整理，得： t x y z vx v y vz d ( )0 dt x y z
d ( v) 0 dt
第一节 微分形式的连续方程
vx v y vz 散度： div( v) v x y z
div ( v) 0 t d div (v) 0 dt
微分形式的连续方程适用于所有流体（粘性、理 想），所有流态（层、紊、亚音速、超音速等）。
第一节 微分形式的连续方程
C G F B
vx dydz
dy
vy
y
D
z
A
x
vz dx vx
dz
E
H
单位时间内ABCD面流入
vx dydz
第一节 微分形式的连续方程
C
G F
vx dydz
B
( vx ) [ vx dx]dydz x
H
dy
vy
y
D
z
A
x
vz dx vx
dz
E
单位时间内EFGH面流出
第五节 理想流体流动的定解条件
运动学条件，例如：固体壁面
流体既不能穿透壁面，也不能脱离壁面而形 成空隙，即流体与壁面在法线方向的相对分速度 应等于零。即：
vn vwn
若固壁是静止的
vn 0 v1n v2 n
在两种不同流体交界面上
第五节 理想流体流动的定解条件
动力学条件
流体在不同流体交界面或固体壁面上的动 力学条件为：外界流体或壁面作用在流体上的 压强Pamb与位于交界面或壁面上该处流体质点 的压强P的绝对值必然相等。
第四节 欧拉积分式和伯努利积分式
由于是定常流动，流场中的流线和迹线重 合，因此dx、dy、dz就是在dt时间内流体微团 的位移ds＝vdt在三个轴向的分量。
dx vx dt
dy v y dt
2
dz vz dt
代入方程组，相加并积分，得：
v pF const 2 对于非粘性的不可压缩流体和可压缩的正压流体， 在有势的质量力作用下作定常有旋流动时，沿同一流线 上各点单位质量流体质量力的位势能、压强势能和动能 的总和保持常数值，而这三种机械能可以互相转换。
pamb p
第四节 欧拉积分式和伯努利积分式
关于理想流体欧拉运动微分方程的积 分，目前仅对几种特殊的流动可以进 行，最常见的有定常无旋流动的欧拉 积分和定常流动的伯努利积分。
第四节 欧拉积分式和伯努利积分式
积分的前提条件：
1. 流动是定常的
vx v y v z 0 t t t t
第二节 流体微团运动的分解
刚体任意参考点的平移速度 绕参考点的旋转速度
刚体的运动速度
流体任一质点速度
质点上任意参考点的平移速 度 绕通过该点的瞬时轴旋转速度 变形速度
第二节 流体微团运动的分解
流体微团的运动
移动
流体微团的运动
转动 变形运动
第二节 流体微团运动的分解
C B G
vy
D
vx dx vx dy vx dz F vx x 2 y 2 z 2
第一节 微分形式的连续方程
对定常流动：
( vx ) ( v y ) ( vz ) 0 x y z
div ( v) 0
( v) 0
对不可压缩流体定常流动：
vx v y vz 0 x y z
div (v) 0
v 0
理想流体的欧拉 运动微分方程组
矢量形式：
dv 1 f p dt
第三节 理想流体的运动微分方程
方程式左边展开：
第三节 理想流体的运动微分方程
欧拉方程对于不可压缩流体和可压缩 流体都是适用的。 当 vx v y vz 0 时欧拉运动微分方程成 为欧拉平衡微分方程。
f 1
第四章 理想流体的无旋和 有旋流动
第七章 理想流体的无旋流动和有旋流动
理想流体运动基本方程组 理想流体基本方程的定解条件及其积 分 理想流体的有旋流动 有势流动 速度势和流函数 几种简单的不可压缩流体的平面流动 及其叠加 平行流绕过圆柱体和机翼的平面流动
理想流体运动基本方程组
第一节 微分形式的连续方程 第二节 流体微团运动的分解 有 旋流动和无旋流动 第三节 理想流体的运动微分方程
v x , v y , v z , p, 5个
还需要增添一个方程，使方程组封闭，才能求解。
对于不可压缩流体， const 对于密度仅是压强的函数的流体
( p)
第五节 理想流体流动的定解条件
方程组的定解条件
初始条件 定解条件 边界条件
第五节 理想流体流动的定解条件
一、初始条件
角变形
通过形心互相垂直的两条中心线直角夹角的减小 量（即变化量）为 d d ，于是得流体微团在垂直 于z轴的平面上的角变形速度分量
d d z 2 dt dt
1 d d 1 v y vx z ( ) ( ) 2 dt dt 2 x y
x
流体微团角变形速 度之半的三个分量
流体微团的旋转角速度的定义为每秒内绕同一转 轴的两条互相垂直的微元线段旋转角度的平均值。
第二节 流体微团运动的分解
流体微团沿z轴的旋转角速度分量
流体微团旋转角 速度的三个分量
第二节 流体微团运动的分解
把以上结果代入F点的速度公式
由此证明，在一般情况下流体微团的运动可分解 为三部分：①随流体微团中某一点一起前进的平移运 动；②绕这一点的旋转运动；③变形运动（包括线变 形和角变形）。
即：控制体内流体质量的增长率＋ 通过界面流出控制体的质量流量＝0
( vx ) ( v y ) ( vz ) 0 t x y z
微分形式的连续方程
第一节 微分形式的连续方程
引入哈密顿算子
i j k x y z
vx v y vz v x y z ( vx ) ( v y ) ( vz ) ( v) x y z
第二节 流体微团运动的分解
线变形
每秒内单位长度的伸长（或缩短）量称为线应变速度
vx 线变形速度： x
v y y
vz z
第二节 流体微团运动的分解
角变形
第二节 流体微团运动的分解
角变形
角变形速度的定义为每秒内一个直角的角度变化量。 记为： 2 ( )
第二节 流体微团运动的分解
第四节 欧拉积分式和伯努利积分式
三、伯努利方程
质量力仅仅是重力 不可压缩流体
gz
const
p
pF
p
v2 gz const 2
理想流体的有旋流动
第六节 涡线 涡管 涡束 涡通量 第七节 速度环量 斯托克斯定理 第八节 汤姆逊定理 亥姆霍兹旋涡定理
第六节 涡线 涡管 涡束 涡通量
p 0
第三节 理想流体的运动微分方程
理想流体的运动微分方程的另一种形式
此方程组称为兰姆（H．Lamb）运动微分方程。
理想流体基本方程组的定解条件及其积分 理想流体基本方程组的定解 条件 欧拉积分式和伯努利积分式 伯努利方程
第五节 理想流体流动的定解条件
方程组的封闭问题
连续方程 运动方程 未知量 1个 3个 4个
初始条件是指在起始瞬时t＝0所给定的流场中 每一点的流动参数。 也就是说，求得的解在t＝0时所应分别满足的 预先给定的坐标函数。
定常流动不需要给定初始条件。
第五节 理想流体流动的定解条件
二、边界条件
边界条件是指任一瞬时运动流体所占 空间的边界上必须满足的条件。 运动学条件：边界上速度 边界条件 动力学条件：边界上的力（压强）