为什么是0.618(一)课件说明
为什么是0.618 PPT课件 2 北师大版

分析 : 主要相等关系是 每台冰箱的销售利润 平均每天销售冰箱的数量 5000元.
如果设每台冰箱降价x元, 那么每台冰箱的定价就是 (2900 x)元,每台冰箱的销售利润为(2900 x 2500)元,
平均每天销售冰箱的数量为(8 4 x )台,这样 50
就可以列出一个方程, 进而解决问题了.
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
19、就算生活让你再蛋疼,也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•
21、所有欺骗中,自欺是最为严重的。
•
22、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。
•
23、天行健君子以自强不息;地势坤君子以厚德载物。
•
24、态度决定高度,思路决定出路,细节关乎命运。
•
25、世上最累人的事,莫过於虚伪的过日子。
•
26、事不三思终有悔,人能百忍自无忧。
•
27、智者,一切求自己;愚者,一切求他人。
•
28、有时候,生活不免走向低谷,才能迎接你的下一个高点。
•
29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。
【例题】
【例2】学校图书馆去年年底有图书5万册,预计到明 年年底增加到7.5万册.求这两年的年平均增长率.
分析:等量关系为经过两年平均增长后的图书=7.5万册.
去年 今年
基数 平均增长率
5
x
年底数量 5
5(1+x)
明年 5(1+x)
x
5(1+x)(1+x)=5(1+x)2
北师大九年级数学上册为什么是0.618

船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送
达军舰.
(2) 已知军舰的速度是补给船的2倍,军舰 A
图 2-8 北
在由B到C的途中与补给船相遇于E处,那么
相遇时补给船航行了多少海里?(结果精确
分到析0.:1海∵里两,船其速中度之6 比 2为.44v9军)舰 2
200
v补给船
∴相同时间内两船的行程之比为
1 s军舰
2
s补给船 1
B
x E?
D 100 F
东
45º C
若设相遇时补给船的行程DE为x海里,则相遇时军舰 200 的行程应为 2x 海里.图上哪一部分对应的是军舰的行程?
例题赏析 1
答:相遇时补给船航行了约118.4海里.
(2) 已知军舰的速度是补给船的2倍,军舰
在由B到C的途中与补给船相遇于E处,那么 A 相遇时补给船航行了多少海里?(结果精确
答:赛义德得到的多的一笔钱数为12.
图 2-8 北
到0.1海里,其中)Fra bibliotek6 2.449
200
D
东
解: 若设相遇时补给船的行程DE为x海里,
x
则相遇时军舰的行程应2x为海里,
100
即 DE x海里, AB BE 2x海里 另外易证 ΔDFC为等腰直角三角形
B E?
FC DF 100 (海里)
EF BC BE FC
200 2x 200100
人在春季感到舒畅,那是因为这时的环境温度正好 在22至24摄氏度之间,而这种气温与人的正常体温 37摄氏度正呈现微妙之处:人的正常体温37摄氏度 与0.618的乘积为22.8摄氏度,人在这一环境温度 中,机体的新陈代谢、生理活动均处于最佳状态。
为什么是0.618(1)

300 2 x ( 海里 )
例题赏析 1
100
x 1 200 x 2 200
100 3 100 3
6 6
118 . 4
在 Rt DEF 中, 根据勾股定理可得方程
建筑
数学的美不同于 其它的美,它是 独特的、内在的, 不华丽,但纯结、 祟高.
艺术
生活
你知道黄金比的近似值0.618是怎样求出来的吗
§2.5为什么是 0.618?
学习目标
黄金比值0.618怎么得来的. 进一步感受方程是刻画现实世界的有 效模型。 会用列方程解决实际问题. 要用数学美去装点和美化生活.
DF BC , AB BC DFC 90 , ABC 90
AB 200 海里 , BC 200 海里
200
D
东
ΔABC 为等腰直角三角形
C 45
1 2
?
DC 1 2
另外易证, DFC
DF
AB 100 (海里)
~ ABC 且相似比 AC
如图2-7,点C把线段AB分成两条线段AC和BC,如果
AC AB BC AC ,
那么点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比. 由 设 ∴
AC AB BC AC ,
得
AC
2
AB BC
1
AB 1, AC x ,
则 BC
A
1 x
x
C
图2-7
B
即 用公式法解这个方程,得
神奇的0.618《五角星中的黄金比》优质课PPT课件

——《义务教育数学课程标准(2011年版)》
题目分析:
1.已知条件: ①黄金比: 把一条线段分成两部分,如果较短的部分与较长的部分之 比等于较长部分与整体长度之比,我们把这个比称为黄金 比(约为0.618:1)。 ②五角星中a:b≈0.618:1
1.前世今生
上册: 测量
01
02
03
04
05
06
上册: 长度单位 初步认识线段
上册:线段
上册: 比的意义、比的性质 会用比解决问题
教材51页:本题
题目背景:
1.前世今生
线段、测 量、比...
黄金比
比例、黄金分割...
2.编写意图
“你知道吗”,介绍了在实际生活中广泛存在的黄金比,使学生充分感受数 学与现实生活的紧密联系,体会数学价值和美感,提高学生的审美能力。
神奇的0.618
五角星中的黄金比
题目来源: 人教版小学数学六年级上册第四单元《比》,教材51页的 “你知道吗”
a:b ≈ 0.618:1
上图中的五角星内还有哪些其他 线段长度符合黄金比吗?
五
题目背景
角
星
题目分析
的
解题思路
黄
金
变式拓展
比
感悟反思
题目背景:
1.前世今生
线段、测 量、比...
题目背景:
解题思路:2.提出问题,学生猜想
b a
a:b ≈ 0.618:1
上图中的五角星内还有哪些其他 线段长度符合黄金比吗?
“综合与实践”是一类以问题为载体、以学生自主参与为主的学习活动。在学习活动中,学生 将综合运用“数与代数”“图形与几何”等知识和方法解决问题。
为什么是0.618(一)演示文稿

3、平均增长(或降低)率问题 平均增长(或降低) 一商店1月份的利润是2500 2500元 一商店1月份的利润是2500元,3月份的 利润达到3000 3000元 利润达到3000元,这两个月的利润平均月 增长的百分率是多少(精确到0.1 0.1%)? 增长的百分率是多少(精确到0.1%)?
巩固练习: 巩固练习:
2
B E
200
C
。 2 DF=CD。 ∴ DF=CF= 2
CD =
2 2
(海里)。 ×100 2 = 100 海里)。
(2)已知军舰的速度是补给船的 倍,军舰在由 到 )已知军舰的速度是补给船的2倍 军舰在由B到 C的途中与补给船相遇于 处,那么相遇时补给船航 的途中与补给船相遇于E处 的途中与补给船相遇于 行了多少海里?(精确到0.1海里 ?(精确到 海里) 行了多少海里?(精确到 海里) A
随堂练习
1、《九章算术》“勾股”章有一题:“今有二人所 、 九章算术》 勾股 章有一题: 勾股” 甲行率七,乙行率三。乙东行, 立。甲行率七,乙行率三。乙东行,甲南行十步而 斜东北与乙会。问甲乙行各几何。 斜东北与乙会。问甲乙行各几何。” 乙 C A 设甲、乙所行时间为x 设甲、乙所行时间为 3x 10 的距离为3x, 则AC的距离为 , 的距离为 甲 甲 AB的距离为 的距离为7x-10 的距离为 B 根据题意可得, 根据题意可得,方程 答案:甲走了 答案:甲走了24.5步,乙走了 步 乙走了10.5步。 步
习题2.8 习题 1、有这样一道阿拉伯古算题:有两笔钱,一多一少, 、有这样一道阿拉伯古算题:有两笔钱,一多一少, 其和等于20,积等于96,多的一笔被许诺赏给赛义德, 其和等于 ,积等于 ,多的一笔被许诺赏给赛义德, 那么赛义德得到多少钱? 那么赛义德得到多少钱? 解:设赛义德得到的钱数为x,则 少的一笔钱数为 设赛义德得到的钱数为 , 20-x,根据题意,得方程:x(20-x)=96 ,根据题意,得方程: ( ) 解这个方程得: 解这个方程得:x1=12, x2=8(不合题意,舍去) , (不合题意,舍去) 答:赛义德得到的钱数为12 赛义德得到的钱数为
§2、5为什么是0.618(第1课时) (1)
2
A
北
整理, 得3x 1200 x 100000 0.
解这个方程,得:
x1 200 100 6 3 118.4,
B
D
E
F
C
x2 200
100 6 3
不合题意, 舍去.
答:相遇时补给船大约航行了118.4海里.
第四环节:巩固新知;(10分钟)
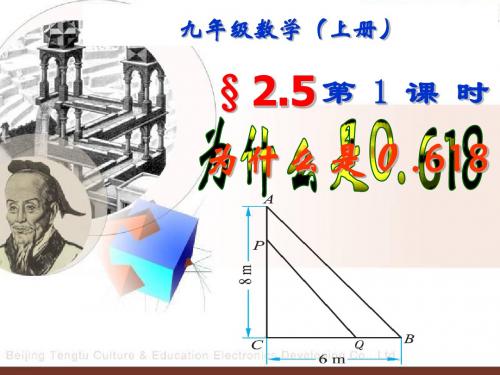
练一练 如图,在Rt△ABC中,∠C=90°,点P,Q同时由A,B两点出发,分 别沿AC,BC方向向点C匀速移动,它们的速度都是1m/s.几秒 后△PCQ的面积是Rt△ACB面积的一半?
x x+10
解这个方程, 得 :
这部分教学设计意图: 在例1的基础上,进一步深化对利用一元二次方程解应用题的认识,体会刚刚归 纳过的解题方法,提高阅读能力
初中数学资源网
主要从以下几个方面分步着手,突破难点
1.结合图形审题,一边读题,一边将题中显而易见的数学量在图中标 示出来。 2.结合问题类型,分析各量之间的关系; 假设未知数,用含未知数的代数式表示出题中的未知量; 3、找等量关系,列方程。
解 :由 AC AB CB AC , 得AC AB CB.
2
1 5 设AB 1, AC x, 则CB 1 x. x1 , 2 x 1 1 x , 2
A
C
B
即x x 1 0.
2
解这个方程, 得
x 1 5 2 .
x2
A P 8 cm
同学们先尝试独立完成,如有难度可 进行小范围的讨论
C
Q 6 cm
B
初中数学资源网
分析
北师大版初中九年级数学上册-《为什么是0.618》教学课件

解 : 设每年的平均增长率为x, 根据题意, 得
5(1 x)2 7.5.
解这个方程 : (1
x)2
3
,
2
(1 x) 6 ,
2
x 1 6 ,
x1 1
6 2
22.48%; x2
2 1
6 0(不合题意,舍去). 2
答 : 每年的平均增长率约为22.48%.
解这个方程,得整理得:x230x250 0.
回顾与思考5
有关利润的知识基本知识
商品利润=售价-进价;
商品利润率
利润 进价
.
驶向胜利 的彼岸
例题欣赏 1
我是商场经理
❖ 例2 新华商场销售某种冰箱,每台进价为250元.市场调 研表明:当销售价为2900元时,平均每天能售出8台;而当 销价每降低50元时,平均每天能多售4台.商场要想使这种 冰箱的销售利润平均每天达到5000元,每台冰箱的定价 应为多少元?
40 x1 40 10 50;40 x2 40 40 80.
600 10 x1 600 100 500;600 10 x2 600 400 200. 答 : 每个台灯的定价应为50元或80元,
进货量相应为5000个或200个.
源于生活,服务于生活 我也参与商场竟争
2. 某商场礼品柜台春节期间购进大量贺年片,一种贺 年片平均每天能售出500张,每张盈利0.3元.为了尽快 减少库存,商场决定采取适当的降价措施.调查表明: 当销售价每降价0.1元时,其销售量就将多售出100张. 商场要想平均每天盈利达到120元,每张贺年片应降 价多少元?
整理得 :
x2
300x
50 22500
0.
解这个方程, 得 x1 x2 150.
《为什么是0.618》教案-01

《为什么是0.618》教案知识目标:1、掌握黄金分割中黄金比的来历;2、经历分析具体问题中的数量关系,建立方程模型并解决问题的过程,认识方程模型的重要性。
教学重点难点:列一元一次方程解应用题,依题意列一元二次方程教学程序:一、复习1、解方程:(1)x 2+2x+1=0 (2)x 2+x -1=02、什么叫黄金分割?黄金比是多少?(0.618)3、哪些一元二次方程可用分解因式法来求解?(方程一边为零,另一边可分解为两个一次因式)二、新授1、黄金比的来历如图,如果AC AB =CB AC,那么点C 叫做线段AB 的黄金分割点。
由AC AB =CB AC,得AC 2=AB ·CB 设AB=1, AC=x ,则CB=1-x∴x 2=1×(1-x) 即:x 2+x -1=0解这个方程,得x 1=―1+52 , x 2=―1―52(不合题意,舍去) 所以:黄金比AC AB =―1+52≈0.618 注意:黄金比的准确数为5 ―12,近似数为0.618.上面我们应用一元二次方程解决了求黄金比的问题,其实,很多实际问题都可以应用一元二次方程来解决。
2、例题讲析:例1:P64 题略(幻灯片)(1)小岛D 和小岛F 相距多少海里?(2)已知军舰的速度是补给船的2倍,军舰在由B 到C的途中与补给船相遇于E 处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)解:(1)连接DF ,则DF ⊥BC ,∵AB ⊥BC ,AB=BC=200海里∴AC= 2 AB=200 2 海里,∠C=45°∴CD=12 AC=100 2 海里 DF=CF , 2 DF=CD ∴DF=CF=22 CD=22×100 2 =100海里 所以,小岛D 和小岛F 相距100海里。
(2)设相遇时补给船航行了x 海里,那么DE=x 海里,AB+BE=2x 海里EF=AB+BC ―(AB+BE )―CF=(300―2x )海里在Rt △DEF 中,根据勾股定理可得方程:x 2=1002+(300-2x)2 整理得,3x2-1200x+100000=0解这个方程,得:x1=200-10063≈118.4 x2=200+10063(不合题意,舍去) 所以,相遇时,补给船大约航行了118.4 海里。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章一元二次方程第五节为什么是0.618(1)ppt说明文稿本ppt文件与一元二次方程第五节为什么是0.618(1)的教学设计配套使用。
按照教学设计的流程分为五个环节。
第一环节:回忆巩固,情境导入 ----以学生所熟悉的黄金分割中的黄金比的求法为素材,引入本节的内容,为第2张幻灯片,使用时,采用点击鼠标即可。
第二环节:做一做,探索新知 ----把教材作为出发点,作为素材来呈现,依据《数学课程标准》,创造性的开发,使用教材。
采取的是一讲一练。
为第3—7五张片,其中第四张片在例题答案出现之后,点击即为相应的巩固练习;第六张片在例题之后,点击即出现另外一种解法的图,第七张片在例题出现之后,依次点击分别出现相关的巩固练习和拓展延伸。
第三环节:练一练,巩固新知——为第8张片,直接点击即可。
第9、10张片为最后两个环节。
