静定结构影响线-3
机动法作静定结构内力影响线依据

机动法作静定结构内力影响线依据机动法是结构力学中的一种常用方法,它通过对静定结构进行虚位移,得到结构内力的影响线。
影响线可以用来计算结构内力,分析结构的稳定性和安全性。
本文将以机动法作静定结构内力影响线为标题,详细介绍该方法的原理和应用。
一、机动法的原理机动法是一种基于虚位移原理的力学分析方法。
它假设结构处于静定平衡状态,通过施加虚位移,得到结构的内力分布情况。
具体的步骤如下:1. 建立坐标系:首先,需要建立合适的坐标系来描述结构的几何形状和受力情况。
2. 施加虚位移:在结构的每个节点处施加虚位移,可以是平移、转动或两者的组合。
虚位移是一个无限小的位移,它满足结构的约束条件。
3. 建立平衡方程:根据结构处于静定平衡状态,可以建立各个节点的平衡方程,包括力平衡和力矩平衡方程。
4. 求解内力影响线:通过解平衡方程,得到结构内力与虚位移之间的关系,即内力影响线。
内力影响线描述了不同位置处的虚位移对内力的影响程度。
5. 计算内力:利用内力影响线,可以计算出结构在不同位置处的内力大小和方向。
二、机动法的应用机动法作为一种常用的静力学方法,广泛应用于结构力学的研究和工程实践中。
具体应用包括以下几个方面:1. 内力分析:机动法可以用来计算结构在各个位置处的内力大小和方向。
通过分析内力的分布情况,可以评估结构的稳定性和安全性。
例如,在桥梁设计中,通过计算桥梁各个位置处的内力,可以确定桥梁的强度和刚度要求。
2. 结构优化:机动法可以用来评估不同结构方案的性能,从而进行结构优化设计。
通过分析不同虚位移对内力的影响,可以找到最优的结构形状和尺寸。
例如,在建筑设计中,可以通过机动法来评估不同楼板厚度对结构内力的影响,从而确定最经济的楼板厚度。
3. 结构安全评估:机动法可以用来评估结构的安全性。
通过分析内力的分布情况,可以确定结构是否存在超过设计强度的部分。
例如,在地震工程中,可以通过机动法来评估结构在地震荷载下的内力分布情况,从而确定结构的安全性。
10(超)静定结构的影响线解析

§9-5 超静定力的影响线1、影响线的特征与求解方法1)影响线的特征静定结构——反力、内力影响线均为直线;位移影响线为曲线。
超静定结构——各量值的影响线均为曲线。
2)影响线的求作方法静力法——利用静力平衡条件求影响线方程,进而绘制影响线。
但对超静定力的影响线须解超静定问题,复杂、少用。
机动法——利用影响线与移动载荷作用点位移(挠度)图的比拟关系,快速绘制影响线轮廓。
简便、实用。
2、机动法求作超静定力影响线以图9-14连续梁(超静定梁)M K的影响线为例,说明用机动法求作超静定力影响线的方法。
1)取基本结构(超静定、几何不变体系)图b——去掉与XK 相应的约束,代之以(暴露出)约束反力XK ;A B C D EF P=1K(a)原结构A B C D EF P=1X K(M K)(下拉为正)(b)基本结构图9-14§9-5 超静定力的影响线2)建立力法典型方程k kk kp X δδ+=1()kp k pk kk kkX x δδδδ∴=-=-⋅()()pk kp x x δδ=ABCD EF P =1K ABCD E F P =1X K (M K )(下拉为正)(b)基本结构§9-5 超静定力的影响线K 截面相对转角为0式中δkk ——常数,不随X 而变化。
δpk ——载荷F P =1位置参数X 的函数,即δPK =δPK (x),其位移图如图9-14c 所示。
互等定理图9-14ABCDEX K (M K )(下拉为正)θB(c)挠度图⏹写成更明确的形式:()()1pk kkk x x X δδ=-ABCD EK+图9-15X k (M k )的影响线结论:X k 与δpk 成正比;挠度图即为影响线轮廓线图9-14ABCDEX K (M K )(下拉为正)θB(c)作用挠度图1kM=§9-5 超静定力的影响线X k 向上为正δpk 以向下为正(与p=1同向)X k 与δpk 反向3、求做超静定力影响线的步骤⏹1)撤去与所求约束力(或量值)相应的约束,代之以反力X K ;●2)使体系沿X K 正方向发生位移,作出移动载荷作用点的挠度δPK =δPK (x)(位移)图即为影响线X K (x)的形状;●3)将δPK 图除以常数δKK 使可确定影响线的具体数值;●4)横坐标以上图形为正号,横坐标以下图形为负号。
作静定结构影响线的三种简单方法

作静定结构影响线的三种简单⽅法作静定结构影响线的三种简单⽅法作影响线的基本⽅法有静⼒法和机动法,但是对于复杂的静定结构,仅仅运⽤静⼒法或机动法求解其内⼒影响线是不够的,往往不能迅速得到正确结果.我们参考资料归纳了三种简便⽅法,并借助例题进⾏阐述.这些⽅法均建⽴在静⼒法、机动法的基础之上,仍然遵循刚体的虚功原理,其处理问题的基本思路可归纳为:⾸先进⾏必要的静⼒计算或分析,考虑是否可以简化处理;再考虑辅以结构等效变形,进⾏结构简化;最后针对简化的机构运⽤机动法进⾏求作,便可迅速⽽⼜准确地确定复杂结构的内⼒影响线.这些⽅法的优点是既可以避开复杂静⼒计算、分段讨论,⼜可以解决机动法不能直接确定复杂静定结构内⼒影响线的难题。
1、结构等效法有些静定结构形式⽐较复杂,可以利⽤刚⽚法则进⾏等效,并且在静定结构中,若等效替代静定结构内部某⼀⼏何不变部分,则只能改变本部分的受⼒⽽不会改变其余部分的反⼒或内⼒.我们可以利⽤静定结构的这⼀特性并结合刚⽚组成法则,等效变形较复杂的静定结构,这样可以简化体系、利于快速求作结构内⼒影响线,这就是所谓的“结构等效法”.有时,复杂静定结构内⼒影响线⽆法直接利⽤机动法进⾏求解,灵活利⽤结构等效法可以解决这⼀难题,⽐如:不能直接利⽤机动法求作静定平⾏弦桁架内⼒影响线,可通过刚⽚法则简化并与相应机动简⽀梁⽐较,从⽽将机动法推⼴到静定平⾯桁架内⼒影响线的求作中;或抓住平⾏弦桁架荷载传递等效于结点荷载这⼀特点,分别考虑上弦承载及下弦承载的情形,并依据上、下弦杆结点位置确定对应结点荷载分布情况,然后借助结点荷载作⽤下的主梁某内⼒影响线求作桁架内⼒影响线.如图所⽰,求作图⽰结构HA的影响线.解:由刚⽚构造规则不难分析,△ADC及△BEC均可视为由铰接的三⾓形依次增加⼆元体形成的⼏何不变体系,故可以取L型刚⽚ADC及BEC进⾏等效替换,从⽽下部分的桁架可以运⽤三铰刚架进⾏等效替换,如下图所⽰.然后利⽤三铰刚架的关系式求作HA的影响线即可.2、斜率分析法由机动法作静定结构内⼒影响线的虚功原理可知:拟求静定结构内⼒Z的影响线,可以撤去与Z相应的约束并使体系沿着Z的正⽅向发⽣虚位移£z=1,此时结构对应的荷载位移图为所求静定结构内⼒Z的影响线.也就是说,在竖向单位移动荷载P=1作⽤下,静定结构内⼒影响线取结构的竖向位移图;在⽔平单位移动荷载P=1作⽤下,静定结构内⼒影响线取结构的⽔平位移图;在单位移动⼒偶M=1作⽤下,静定结构内⼒影响线取结构的转⾓位移图,⽽当转⾓位移很⼩时,有等价关系,所以此时结构内⼒影响线可取竖向位移图的斜率.影响线竖距的正负号可规定如下:当结构转⾓位移⼝与单位移动⼒偶M=1⽅向⼀致时,取负号;反之,取正号.这就是所谓的“斜率法”,此种⽅法仅适⽤于求解静定结构在单位移动⼒偶M=1作⽤下的内⼒影响线.如图所⽰,试求作图⽰结构在单位移动⼒偶m=1作⽤下的Mc、Qc的影响线.解:分别撤去所⽰静定结构与Mc、Qc相应约束,并令结构分别沿其正⽅向发⽣的虚位移为“l”,然后分别作出结构的竖向位移图,如图所⽰,最后分别取结构竖向位移图的斜率即为所求图⽰结构Mc、Qc 的影响线,分别如图所⽰.3、联合分析法静定结构的内⼒影响线由分段的直线段组成,故可先运⽤机动法分析静定结构影响线的轮廓特征即影响线有⼏段及其相互位置关系(铰接或平⾏),再利⽤静⼒法确定各直线段特征点竖标便可确定所求静定结构的内⼒影响线,这就是所谓的“联合分析法”。
静定结构某一截面某一内力的影响线

静定结构某一截面某一内力的影响线在结构力学中,影响线是一种描述结构内力和变形的图形工具。
在静定结构中,影响线的应用可以帮助我们快速而准确地计算结构的内力和变形。
本文将以静定结构某一截面某一内力的影响线为标题,为大家介绍影响线的原理、计算方法及应用。
我们需要了解什么是影响线。
影响线是指沿着结构中某个点或者某个截面上的一个虚拟荷载移动时,该点或该截面内力的变化情况。
影响线的作用是将实际荷载转化为相应的内力,从而方便我们进行计算。
在计算影响线时,我们需要使用弹性力学的基本原理。
根据弹性力学原理,结构内力与荷载的关系可以表示为:内力=荷载*影响线其中,影响线是一个比例系数,表示荷载作用在某一点或某一截面上时,该点或该截面内力的变化情况。
因此,我们可以通过计算影响线来求解结构的内力。
接下来,我们来看看如何计算影响线。
一般来说,计算影响线需要分为以下几个步骤:1.选择荷载的作用点或截面,确定荷载类型和大小。
2.在荷载作用点或截面上引入一个虚拟荷载,通常我们会选择一个单位荷载,即荷载大小为1。
3.计算结构在虚拟荷载作用下的内力和变形。
这一步需要使用力学知识和计算方法,例如静力平衡、弹性力学等。
4.根据弹性力学原理,计算虚拟荷载作用下的影响线。
影响线的计算公式为:影响线 = 内力/荷载5.重复以上步骤,分别在荷载作用点或截面的不同位置引入虚拟荷载,并计算其对应的影响线。
通过以上步骤,我们就可以得到荷载作用点或截面上不同位置的影响线。
影响线的图形通常为一条曲线,其纵坐标表示内力的大小,横坐标表示荷载作用点或截面的位置。
影响线的形状和位置与结构的刚度、荷载类型和大小等因素有关,因此我们需要针对不同的荷载类型和内力位置计算相应的影响线。
我们来看看影响线的应用。
在结构设计和分析中,影响线是一种常用的计算工具。
通过计算影响线,我们可以快速而准确地求解结构在不同荷载作用下的内力和变形,从而进行结构设计和分析。
例如,在桥梁设计中,我们可以通过计算不同位置的影响线,确定桥梁各部位的内力和变形,以保证桥梁的安全和稳定。
结构力学-影响线

第四节
结点荷载下的影响线
P=1 P=1P=1 横梁 P=1 纵梁 C
D d/2 d/2 E
结点荷载下影响线特点 1、在结点处,结点荷载与 A 直接荷载的影响线竖标相同。 2、相邻结点之间影响线为 RA 一直线。 结点荷载下影响线作法 1、以虚线画出直接荷载 作用下有关量值的影响线。 2、以实线连接相邻结点 处的竖标,即得结点荷载作 用下该量值的影响线。
K
l/4
1
第二节
静力法作静定梁的影响线
3、静力法求伸臂梁的影响线 ①作伸臂梁的反力及跨间截面内力影响线时,可先作 出无伸臂简支梁的对应量值的影响线,然后向伸臂上延 伸即得。 ②伸臂上截面内力影响线,只在截面以外的伸臂部分有 非零值,而在截面以内部分上影响线竖标为零。
D
A c
C a l b
B c
E
以 A 点为坐标原点,向右为坐标轴正向,建立影响线方 程,指出方程适用范围,绘制影响线图形。
第三节
机动法作静定梁的影响线
x C l
1
虚功法做影响线举例 P=1 x C a b l 1 C QC b/l
- +
P=1 b b P=1
a
P=1
C ab/l
+ - -
a/l I.L.QC
I.L.MC
第三节
机动法作静定梁的影响线
虚功法做影响线举例 多跨静定梁含基本部分和附属部分,用机动法比较方便。 K E A
机动法绘制影响线的优点:不经具体的静力计算即可迅速
确定影响线的形状、正负号和控制纵标,特别是影响线中各直 线段落与撤去约束后的体系内各刚体的分界相对应,这为结构 设计工作提供了方便,也可为静力法所做的影响线进行校核。
第四节
第4章静定结构影响线
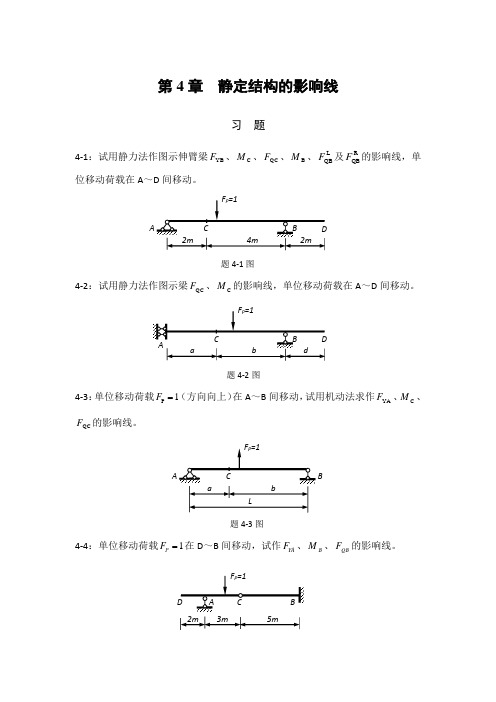
第4章 静定结构的影响线习 题4-1:试用静力法作图示伸臂梁YB F 、C M 、QC F 、B M 、L QB F 及RQB F 的影响线,单位移动荷载在A ~D 间移动。
题4-1图4-2:试用静力法作图示梁QC F 、C M 的影响线,单位移动荷载在A ~D 间移动。
题4-2图4-3:单位移动荷载P 1F =(方向向上)在A ~B 间移动,试用机动法求作YA F 、C M 、QC F 的影响线。
题4-3图 4-4:单位移动荷载1P F =在D ~B 间移动,试作YA F 、B M 、QB F 的影响线。
BA题4-4图4-5:单位移动荷载P 1F =在A ~G 间移动,试作YA F 、B M 、QF F 的影响线。
题4-5图4-6:试用机动法做题4-2。
4-7:试用机动法做题4-4。
4-8:试用机动法做题4-5。
4-9:单位移动荷载P 1F =在A ~F 间移动,试用机动法求YB F 、C M 、YD F 、QE F 的影响线。
题4-9图4-10:单位移动荷载P 1F =在A ~G 间移动,试用机动法求作A M 、YB F 、QB F 、YC F 的影响线。
题4-10图4-11:当P 1F =沿A ~B 移动时,试作图示结构YD F 、K M 的影响线。
题4-11图4-12:当P 1F =在上层梁移动,试用静力法作图示结构的QG F 、H M 的影响线。
题4-12图4-13:如图所示单位力P 1F =在AB 、CD 杆上移动,请分别用静力法和机动法作YA F 及QF F 的影响线。
题4-13图4-14:试作图示主梁YC F 、F M 、QF F 、L QE F 、RQE F 的影响线。
题4-14图4-15:试求图示结构QC F 、QB F 的影响线,单位荷载P 1F =在E ~F 间移动。
AA DBEB C题4-15图4-16:试作桁架指定杆件轴力的影响线,单位荷载P 1F =在下弦移动。
第八章 静定结构影响线

A RA A a b 2 c d e f g
NbC
P=1 B
P=1 2
C
l=6d
D
D
E
F
可概括为一个式子
0 YbC QBC
B
C
P=1 E
F
G
x
RG 2/3
+ -1/6
平行弦桁架斜 RA 杆轴力的YbC影响 线就是±梁的节 间剪力QBC0影响线。 右下斜为正,右 上斜为负。
B
C
l=6d
D
E
F
10
h
G
§8-4静力法作桁架的影响线
任一轴力影响线 在相邻结点之间为 直线。 反力影响线与简 A 支梁相同。 平行弦桁架弦杆 影响线可由相应梁 结点的弯矩影响线 竖标除以h得到。 上弦杆为压 下弦杆为拉。
RA a b N1 bc c d e P=1 D E F f g
B
NCD C 1
1
x a C i
P=1
l
x Z(x) 1
+ -
P=1 δP(x)
Z ( x) 1 1 P ( x) 0 Z ( x) P ( x)
Z 的影响线, P=1 作用点的竖 基线以上的竖 向虚位移图,向 下为正(与P=1 标为正 同向)。
于是得到:所得虚位移图即 Z 的影响线。基线以上的虚位 移图是正影响线,基线以下的 虚位移图是负影响线。
b/l + - a/l
ab/l
QC.I.L
-
+ Mc.I.L QD .I.L
MD.I.L
_
+ 1
-
作静定结构影响线的三种简单方法

作静定结构影响线的三种简单方法作影响线的基本方法有静力法和机动法,但是对于复杂的静定结构,仅仅运用静力法或机动法求解其内力影响线是不够的,往往不能迅速得到正确结果.我们参考资料归纳了三种简便方法,并借助例题进行阐述.这些方法均建立在静力法、机动法的基础之上,仍然遵循刚体的虚功原理,其处理问题的基本思路可归纳为:首先进行必要的静力计算或分析,考虑是否可以简化处理;再考虑辅以结构等效变形,进行结构简化;最后针对简化的机构运用机动法进行求作,便可迅速而又准确地确定复杂结构的内力影响线.这些方法的优点是既可以避开复杂静力计算、分段讨论,又可以解决机动法不能直接确定复杂静定结构内力影响线的难题。
1、结构等效法有些静定结构形式比较复杂,可以利用刚片法则进行等效,并且在静定结构中,若等效替代静定结构内部某一几何不变部分,则只能改变本部分的受力而不会改变其余部分的反力或内力.我们可以利用静定结构的这一特性并结合刚片组成法则,等效变形较复杂的静定结构,这样可以简化体系、利于快速求作结构内力影响线,这就是所谓的“结构等效法”.有时,复杂静定结构内力影响线无法直接利用机动法进行求解,灵活利用结构等效法可以解决这一难题,比如:不能直接利用机动法求作静定平行弦桁架内力影响线,可通过刚片法则简化并与相应机动简支梁比较,从而将机动法推广到静定平面桁架内力影响线的求作中;或抓住平行弦桁架荷载传递等效于结点荷载这一特点,分别考虑上弦承载及下弦承载的情形,并依据上、下弦杆结点位置确定对应结点荷载分布情况,然后借助结点荷载作用下的主梁某内力影响线求作桁架内力影响线.如图所示,求作图示结构HA的影响线.解:由刚片构造规则不难分析,△ADC及△BEC均可视为由铰接的三角形依次增加二元体形成的几何不变体系,故可以取L型刚片ADC及BEC进行等效替换,从而下部分的桁架可以运用三铰刚架进行等效替换,如下图所示.然后利用三铰刚架的关系式求作HA的影响线即可.2、斜率分析法由机动法作静定结构内力影响线的虚功原理可知:拟求静定结构内力Z的影响线,可以撤去与Z相应的约束并使体系沿着Z的正方向发生虚位移£z=1,此时结构对应的荷载位移图为所求静定结构内力Z的影响线.也就是说,在竖向单位移动荷载P=1作用下,静定结构内力影响线取结构的竖向位移图;在水平单位移动荷载P=1作用下,静定结构内力影响线取结构的水平位移图;在单位移动力偶M=1作用下,静定结构内力影响线取结构的转角位移图,而当转角位移很小时,有等价关系,所以此时结构内力影响线可取竖向位移图的斜率.影响线竖距的正负号可规定如下:当结构转角位移口与单位移动力偶M=1方向一致时,取负号;反之,取正号.这就是所谓的“斜率法”,此种方法仅适用于求解静定结构在单位移动力偶M=1作用下的内力影响线.如图所示,试求作图示结构在单位移动力偶m=1作用下的Mc、Qc的影响线.解:分别撤去所示静定结构与Mc、Qc相应约束,并令结构分别沿其正方向发生的虚位移为“l”,然后分别作出结构的竖向位移图,如图所示,最后分别取结构竖向位移图的斜率即为所求图示结构Mc、Qc 的影响线,分别如图所示.3、联合分析法静定结构的内力影响线由分段的直线段组成,故可先运用机动法分析静定结构影响线的轮廓特征即影响线有几段及其相互位置关系(铰接或平行),再利用静力法确定各直线段特征点竖标便可确定所求静定结构的内力影响线,这就是所谓的“联合分析法”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
<0
∆x ∆Z ≥ 0
x
成为极小值的临界位置必须满足的条件: 使Z成为极小值的临界位置必须满足的条件: 成为极小值的临界位置必须满足的条件
∆Z ≥ 0, 即∆x ∑ Ri ⋅ tan α i ≥ 0
∆x > 0 ∑ Ri ⋅ tan α i ≥ 0 ∆x < 0 ∑ Ri ⋅ tan α i ≤ 0
∆x > 0
∑ Ri ⋅ tan α i ≤ 0
∆x < 0
∑ Ri ⋅ tan α i ≥ 0
§4-6 影响线的应用
R 1
y1
α1 > 0
∆y
R2
R3
∆Z = ∑ Ri ⋅ ∆yi = ∑ Ri ⋅ ∆x ⋅ Байду номын сангаасan α i = ∆x ∑ Ri ⋅ tan α i
Z
α2 > 0
y2
∆x
y3 α
3
a
利用影响线计算在位置确定的荷载作用下某一量值 大小的方法如下: 大小的方法如下: 作出某一量值S的影响线 的影响线; ① 作出某一量值 的影响线; 利用下式求出该量值的大小。 ② 利用下式求出该量值的大小。
S = ∑ FPi × yi + ∑ ωi qi
i =1 i =1
n
n
§4-6 影响线的应用
§4-5 机动法画影响线
(2)求简支梁弯矩的影响线
Fp=1 A a C b B
真实的力状态
点的抗弯约束去掉, 把C点的抗弯约束去掉,用一对力矩 C代替,得 点的抗弯约束去掉 用一对力矩M 代替, 到一个机构,让该机构沿着力矩M 到一个机构,让该机构沿着力矩 C的方向发生一个 虚位移, 虚位移,设C点发生的相对转角 α + β = 1 。 点发生的相对转角
§4-5 机动法画影响线
a
α
α +β=1
b
虚设的位移状态
β
MC
令真实的力到虚设的位移上做虚功,由虚功方程: 令真实的力到虚设的位移上做虚功,由虚功方程: δp M C × α + M C × β − 1× δ P = 0 ② MC = = δ p … …② α +β 由式②可知,虚位移图就是 的影响线。 由式②可知,虚位移图就是MC的影响线。
§4-6 影响线的应用
例:下图为某一量值的影响线及一组移动荷载, 下图为某一量值的影响线及一组移动荷载, F=90kN,q=37.8kN/m,求荷载的临界位置及临界值。 , ,求荷载的临界位置及临界值。 解:取图示荷载位置进 行验算: 行验算:
3.5m 1.5 1.5 1.5 1.5 1.5 7m
虚设的位移状态
δz =1 F
QC
§4-5 机动法画影响线
令真实的力到虚设的位移上做虚功,由虚功方程: 令真实的力到虚设的位移上做虚功,由虚功方程: FQC × δ z − 1× δ P = 0 δp FQC = = δ p ……③ ③ δz 由式③可知, 的影响线。 由式③可知,虚位移图就是 FQC的影响线。
(1)一个集中荷载 (2)一组集中荷载
§4-6 影响线的应用
(3)任意分布荷载
q
q
max
q
min
§4-6 影响线的应用
3)确定移动集中荷载的临界位置
如果移动荷载是一组集中荷载,要确定某量值 的最不利 如果移动荷载是一组集中荷载,要确定某量值Z的最不利 荷载位置,通常分为两步进行: 荷载位置,通常分为两步进行: (1)求出使 值达极值时的荷载位置 称临界位置。 求出使Z值达极值时的荷载位置 称临界位置。 求出使 值达极值时的荷载位置,称临界位置 (2)从各个临界位置中选出荷载的最不利位置。 从各个临界位置中选出荷载的最不利位置。 从各个临界位置中选出荷载的最不利位置
§4-5 机动法画影响线
a
ab l
b
Mc影响线
§4-5 机动法画影响线
(3)求简支梁剪力的影响线 )
Fp=1 A a C b B
真实的力状态
点的抗剪约束去掉, 把C点的抗剪约束去掉,用一对剪力 QC代替,得到 点的抗剪约束去掉 用一对剪力F 代替, 一个机构,让该机构沿着剪力F 一个机构,让该机构沿着剪力 QC的方向发生一个虚位 点发生的相对错动: 移,设C点发生的相对错动: δz =1 。 点发生的相对错动
tan α i 是常数,只有各段 是常数,
R 1
y1
α1 > 0
∆y
R2 Pcr
R3
改变数值时, 内的合力 Ri 改变数值时, 上式才可能改变符号。 上式才可能改变符号。荷载 移动时, 改变数值, 移动时,要使 Ri 改变数值,
α2 > 0
y2
∆x
α 3 < 0 则在临界位置必须有一个集 y3
中荷载正好作用在影响线的 顶点上。 顶点上。
+Z 0 -Z
x
§4-6 影响线的应用
R1 1 R
△x
RR2 2
RR3 3
Z = R1 ⋅ y1 + R2 ⋅ y2 + R3 ⋅ y3 = ∑ Ri ⋅ yi
3 i =1
y1
α1 > 0
∆y
α2 > 0
y2
∆x
+ R2 ⋅ ( y2 + ∆y2 ) + R3 ⋅ ( y3 + ∆y3 ) = Z + ∑ Ri ⋅ ∆yi
第4章 静定结构影响线
§4-5 机动法画影响线
机动法画影响线运用的是虚位移原理。 机动法画影响线运用的是虚位移原理。 (1)求简支梁反力的影响线
Fp=1 A B
真实的力状态
的约束去掉, 代替, 把支座A的约束去掉,用力 代替,得到一个机构, 支座 的约束去掉 用力Z代替 得到一个机构, 让该机构沿着力Z的方向发生一个虚位移 设与Z相应 的方向发生一个虚位移, 让该机构沿着力 的方向发生一个虚位移,设与 相应 的虚位移为δz,如下图所示。 的虚位移为 ,如下图所示。
§4-6 影响线的应用
R 1
y1
α1 > 0
∆y
R2 Pcr
R3
临界位置
α2 > 0
y2
∆x
y3 α
3
<0
临界荷载
总结: )选一个荷载P 置于影响线的某个顶点; 总结: 1)选一个荷载 cr置于影响线的某个顶点; 2)当Pcr在该顶点稍左或稍右时,分别求 ∑ Ri ⋅ tan α i ) 在该顶点稍左或稍右时, 的数值,看其是否变号, 的数值,看其是否变号,从而确定此位置是否是临 界位置 3)对每个临界位置可求出一个 的极值,选出最大值 的极值, )对每个临界位置可求出一个Z的极值 或最小值
2m 1m 2m
D A B 1.0 C E F G H
I.L QA
0.25
§4-6 影响线的应用
1)当荷载位置确定时求某量值的大小 简支梁反力F 的影响线如下所示,其中C点的 简支梁反力 YA的影响线如下所示,其中 点的 是单位力作用在C点时 反力F 的大小。 点时, 竖标 yc是单位力作用在 点时,反力 YA的大小。 若C点作用一集中力 FP时,显然 FYA = FP × yc 点作用一集中力 若简支梁上作用有一 Fp 组位置确定的荷载时, 组位置确定的荷载时, yc 1 FYA的计算如下: 的计算如下: C
∆y
R2
R3
∆Z = ∑ Ri ⋅ ∆yi = ∑ Ri ⋅ ∆x ⋅ tan α i = ∆x ∑ Ri ⋅ tan α i
α2 > 0
y2
∆x
y3 α
Z
3
<0
∆x ∆Z ≤ 0
x
成为极大值的临界位置必须满足的条件: 使Z成为极大值的临界位置必须满足的条件: 成为极大值的临界位置必须满足的条件
∆Z ≤ 0,即∆x ∑ Ri ⋅ tan α i ≤ 0
点的弯矩。 例:利用影响线,求出图示梁C点的弯矩。 利用影响线,求出图示梁 点的弯矩
10kN 2kN/m B
2m 1 0.5 0.5
5kN
解:作C点的弯矩影响 点的弯矩影响 线如下所示 。
C A
1m 1m
D
1m 1m 1m
MC影响线
0.25
1× 2 1 × 0.5 M C = 10 × 0.5 + ×2− × 2 − 5 × 0.25 = 5.25kN ⋅ m 2 2
Fp1 Fp2 Fpi Fpn A B
y1
y2
yi
yn
FYA = ∑ FPi yi
B
i =1
n
A
§4-6 影响线的应用
若简支梁上作用有位置确定的均布荷载时, 若简支梁上作用有位置确定的均布荷载时,FYA a、b间影响线 面积代数和 的计算如下: 的计算如下:
q a b
b
FYA = ∫ yqdx = ω q
§4-5 机动法画影响线
因此,机动法作影响线的具体步骤是: 因此,机动法作影响线的具体步骤是: 要求哪一点哪个量值的影响线, a、要求哪一点哪个量值的影响线,就把相应的约束 去掉,用未知力Z来代替(称为真实的力状态 真实的力状态); 去掉,用未知力Z来代替(称为真实的力状态); b、让去掉约束后的机构沿着力的正方向发生虚位移 δz(称为虚设的位移状态),作出荷载作用点的竖 称为虚设的位移状态),作出荷载作用点的竖 虚设的位移状态), 向位移图,即为Z的影响线轮廓图; 向位移图,即为Z的影响线轮廓图; 可进一步定出影响线各竖标的数值, c、令δz =1,可进一步定出影响线各竖标的数值,横 可进一步定出影响线各竖标的数值 坐标以上的图形,影响系数为正号; 坐标以上的图形,影响系数为正号;横坐标以下的 图形,影响系数取负号。 图形,影响系数取负号。
