第一段导线评差计算表
利用Excel表格进行导线的近似平差计算

理 论研 究 苑
2 2 1
利用E cl x e表格进 行导线 的近似平差计算
杨勇军 ,黄 奎树 ,欧阳云
( 江西有色地质勘 查二队 ,江西赣州 3 10 4 0 0)
摘
要 合理利fE cl l f xe 表格特性与测量传统计算方法相结合 ,在E cl 格中进行 附合 导线绕近似平差及导 线坐标点计算 ,对 xe 表
公 路 工 程 为带 状ቤተ መጻሕፍቲ ባይዱ工程 , 因此 ,在路 线 的控 制测 量 中以 布设
附 合 导线 为 主 ,导 线 的平差 及 坐 标计 算 ,工作 量 大 ,程序 繁 琐 , 计 算精 度 要 求 高 ;特别 是 当测 区 的 面积 较大 ,导线 数 量较 多 时 , 计 算更 加 复 杂 ,如果 借 助计 算 器 手算 ,则计 算 时 间长 ,且 容 易 出
现 。 同理 在 O 5~0 1 元格 中处 复 N o1语 句填 充 N o1 1 4单 3 5一O 1 4 单 元 格 ,计 算 其 它 导 线 边 的 方 位 角 。Q 1 4 ,R1 R 1 ,计 算 5 4中 其 它 导 线 点 增 量 值 。在 ¥ 4 4 分 别 编 制 语 句 = ( 1 + 4 一 4 、T 4 一w 2 Q 4 w4 、)一X1+ 4 一 4 )按 “ 号 ” 原则 计 算 坐标 增 量 闭合 差 o = ( 2 R 4 X 0= 反 f、f。按 “ x y 距离 占有比分摊 ”原则将f 、f值分摊到各个导线 x y 坐标 点 。在 S3 1 分别 编 制语 句 ¥ 4 P 3P 4 T 4 P 3P 4 1 、T 3 4 " 1/4 、= 4 * 1/4 计 算 出第 一 个 导 线 点 的 改 正 距 ,复 制 该 两 单 元 格 语 句 分 别 填 充 N s 5~s 1 1 T 1 ,计 算 出其 它导 线 点 增 量 改 正 距 。将 1 4 ,T 5~ 4 中 改 正 距 + 标 增 量 即 可 求 得 改 正 后 的 坐 标 增 量 ,在 U1 、V1 分 坐 3 3 别 编 制 语 句 = 3 S 3 R1 + 1 , 同理 复 制 该 两 单 元 格 语 句 Q1 + 1 、= T 3 3 分 别 填 充 到 u1 5~U l 4 ,V1 5~V 1 ,计 算 出改 正 后 的坐 标 增 4中 量值 。
导线平差计算表格及解析

闭合导线坐标计算
注:黄色部分为外业测量出的或者是已知的;
“n”:多边形内角的个数;
“ƒβ容”:图根导线角度闭合差的容许值为±60″√n,当图根导线作为测区的首级控制网时为±40″√n;
β=β测-ƒβ n;
在这儿坐标方位角的计算就不说了;
△x i,1+i=D i,1+i*cosαi,1+i; △y i,1+i=D i,1+i*sinαi,1+i;
ƒx=Ʃ△x,ƒy=Ʃ△y;
导线全长闭合差ƒ=√(ƒ2x+ƒ2y),相对闭合差K=ƒ∕ƩD,图根导线的容许相对闭合差K容=1∕2000,当K<K容时则说明符合精度要求,可以进行调整,
υ△xi,1+i=-(ƒx∕ƩD)*D i,1+i,υ△yi,1+i=-(ƒy∕ƩD)*D i,1+i;
△x △y x y
υ△xi,1+i υ△yi,1+i ±±
△x i,1+i
△y i,1+i
Ʃ
ƩD ƒx ƒy
辅助计算
观测角 (β测) ′ ″改正数
(β) 改正后角度 ′ ″
坐标方位角 ′ ″
56序号1234△x′△y′ƒβ角度闭合差=Ʃβ测-Ʃβ
理=Ʃβ测-(n-2)*180; ƒβ
≤ƒβ容;
ƒx=Ʃ△x,ƒy=Ʃ△y; ƒD =√(ƒ2x +ƒ2y )
注:1、附合导线和闭合导线的差别在于两个方面:①角度闭合差的计算和调整,②坐标增量闭合差的计算;(怎么计算就不一一说了,见谅!)
坐标增量 m 改正后增量 m
坐标值 m 距离 m。
导线平差计算-有公式的

pl
12665801 ,6284.59
1.128985619
21573364
5
pl
,
3241.495
5849.632 3241.496 D04 -317.116 -121.738
pl
88570519 ,5849.63
3.451335266
20700136
7
pl
,
3119.758
5532.516 3119.758 D07 -151.079 158.247
D*cosα D*sinα
287.4434
G004 190.4928
0.0000
190.4928 298.3402
381.247 182.309 -334.833
H11
64.4110
0.0000
64.4110
183.1512
435.664 -434.962 -24.725
D04 197.4449
0.0000
D06 118.2511
0.0000 118.2511
D06 118.2511
0.0000
118.2511
36.5735
571.483 456.649 343.606
H15
70.4659
G004
0.0000
70.4659
287.4434
∑ 1439.5958
-0.0002
2981.092 -162.968 509.339
2.066814052
51139453
2
pl
,
pl
4110.362 ,5939.32
1.235397374
6
G004
1-11单导线条件平差计算--附合导线坐标条件方程

平差值条件方程: ALˆ A0 0
改正数条件方程: AV W 0
STEP1
表达成角度和边
长平差值的形式
STEP2
表达成角度和边
长改正数的形式
附合导线坐标条件方程
1、纵坐标附合条件方程式
xˆN 1 xC 0
STEP1
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
3
N
SN-1
SN
D
TCD
βN+1
C (N+1)
纵坐标符合条件方程式就是:xˆN 1 xC 0 横坐标符合条件方程式就是:yˆ N 1 yC 0
B点坐标的已知值 (xB , yB ) 或 (x1, y1)
C点坐标已知值
(xC , yC ) 或 (xN 1, yN 1)
C点坐标观测值
A
D
β2
β4
βN
2
4
β1 S1 S2 β3 S3
N
SN-1
SN βN+1
3
B(1)
附合导线示例图
C(N+1)
附合导线坐标条件方程
补充:具体计算时的单位选取
如果x、y 以米为单位,w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
STEP2
表达成角度和边 长改正数的形式
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
非线性从这个式子着手!!
Tˆi TAB ˆ j
i
180
1-12单导线条件平差计算--单一闭合导线条件方程

A
三个条件方程:
1.多边形内角和闭合条件(1个)
N
SN-1
βN
SN βN+1 β1
N-1 βN-1
2.纵、横坐标增量闭合条件(2个)
β2
B(1)(N+1) S1 2
S2
β3 β4
3
S3
4
闭合导线示例图
单一闭合导线条件方程
1.多边形内角和闭合条件
由于导线网构成了多边形,其 N 个转折角的平差值应满足多边形内角和条件。
单一闭合导线条件方程
2.纵、横坐标增量闭合条件(2个)
如果x、y 以米为单位,w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
wx
0
[sin Ti
vSi ]1N
1
[(
x
N
1
xi )vi ]1N
wy
改正数条件方程式-纯量形式
A
[vi
]N 1 2
w
0
[cos Ti
vSi ]1N
1 2062.65
[(
y
N
1
yi )vi ]1N
wx
0
N
SN-1
βN
SN βN+1 β1
N-1 βN-1
[sin Ti
vSi ]1N
1 2062.65
[(
x
N
1
xi )vi ]1N
wy
0
导线测量平差记录表
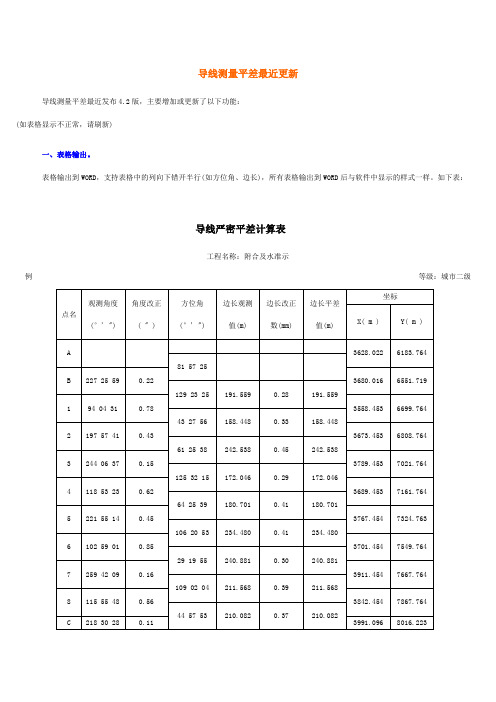
导线测量平差最近更新导线测量平差最近发布4.2版,主要增加或更新了以下功能:(如表格显示不正常,请刷新)一、表格输出。
表格输出到WORD,支持表格中的列向下错开半行(如方位角、边长),所有表格输出到WORD后与软件中显示的样式一样。
如下表:导线严密平差计算表工程名称:附合及水准示例等级:城市二级计算者:杨运英校核者:日期:2003.08.28二、导线采用近似平差且方位角边长不进行反算时的表格样式。
原表格中显示的是坐标增量改正数,现增加了一个选项,可以选择显示改正后的坐标增量,以满足一些工程要求格式统一的要求。
导线平差计算表工程名称:附合及水准示例等级:城市二级计算者:杨运英校核者:日期:2003.08.28、坐标导线平差。
指使用全站仪直接观测坐标、高程的闭、附合导线,其中平面坐标完全差的分配方式可以选用“按边长”、“按坐标增量”、“坐标转换”等方式。
坐标导线平差计算表工程名级:城市二级:杨运英校核者:日期:200四、单面单程水准记录计算已知点较密时线路中间也可以穿过已知点。
当含有中视时可以用于中平测量等,表格形式如下:水准测量记录计算表测线:仪器:观测:天气:地点:记录:计算者:校核者:日期:不含有中视时可用于五等、等外水准等的记录、计算。
表格形式如下:水准测量记录计算表测线:仪器:观测:天气:地点:记录:计算:校核:日期:部测量知点设站,后视另一已知点,观测各碎部点,计算其坐标、高程,绘制图形并可输出到CAD。
方式可以选用“斜距+天顶距”、“平距+高差”或“视距+天顶距”。
距+高差”方式表格如下:碎部测量记录后视:B 测站高程:仪高:气:复核:距”(或“斜距+天顶距”)表格如下:碎部测量记录后视:B 测站高程:指标差:0" 天气:记录:日期:坐标转换于同椭球的不同坐标系间进行转换。
比如同椭球的国家坐标系与工程独立坐标系的转换。
坐标转换计算表工程名第页计算:复核:日期:支导线计算里指输入方位角与边长计算坐标的支导线,如需输入水平角、边长计算各点坐标,请使用“平差计算”模块中的支导线进行计算。
(整理)导线测量平差教程—计算方案设置

计算方案的设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线及导线网、高程网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化,也可以只选择其中的一项改正。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、等级与限差1.在选择好导线类型后,再选择平面及高程的等级,以便根据《工程测量规范》自动填写限差等设置。
如果填写的值不符合您所使用的规范,则再修改各项值的设置。
比如现行的《公路勘测规范》的三级导线比《工程测量规范》的三级导线要求要低一些。
2.导线测量平差4.2及以前版本没有设置限差,打开4.2及以前版本时请注意重新设置限差。
四、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。
1-10单导线条件平差计算--附合导线方位角条件方程-修改

坐标方位角条件就是: TˆN 1 TCD 0
TˆN 1 TCD 0
代入
TˆN 1
TAB
[ˆi
]N 1
1
(N
1) 180
? 思考
TCD TN 1 TˆN1
TAB [ˆi ]1N 1 (N 1) 180 TCD 0 代入 ˆi i vi (i 1,2,, N 1)
[vi ]1N 1 wT 0
wT (TAB [i ]1N 1 (N 1) 180 TCD ) (TN 1 TCD )
A
D
β2
β4
βN
坐标方位角改正数条件方程: [vi ]1N 1 wT 0
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
( xˆ N 1,yˆ N 1 )
条件方程类型:
1坐标方位角附合条件方程式 2纵坐标附合条件方程式 3横坐标附合条件方程式
A
D
β2
β4
βN
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
SN βN+1
C(N+1)
附合导线示例图
理论
感谢聆听,批评指导
公式
思考
平差
算例
Xi’an University of Science & Technology
举一 反三
治学 严谨
Error Theory and Surveying Adjustment
逻辑
性强
主讲人:史经俭 张静 席晶
本讲内容
附合导线方位角条件方程
