人教版数学五年级下册知识链接
人教版五年级数学下册中知识点、易错点、易错题汇总

;4知识点易错点汇总★知识点归纳一、轴对称1、定义:把一个图形沿着某一条直线对折,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴。
折叠后重合的点是对应点,叫做对称点。
2、性质:对称点到对称轴的距离相等。
3、轴对称图形:指具有特殊形状的一个图形,它可以有一条或多条对称轴。
二、旋转1、定义:把一个图形绕某一点(或轴)转动一定的角度的图形变换叫做旋转。
2、旋转三要素:旋转点(旋转中心)、旋转方向、旋转角度钟表中指针运动的方向为顺时针方向,与钟表中指针的运动方向相反的方向为逆时针方向。
3、性质:图形绕着某一点旋转一定的度数,图形的对应点、对应线段都旋转了相应的度数,对应点到旋转点的距离相等,对应的线段和对应的角度相等。
图形旋转后,形状、大小都没有发生变化,只有位置变了。
4、旋转90°的方法(1)找出原图行的关键点或关键线段;(2)借助三角板或量角器作原图行关键点或线段与旋转中心所在线段的垂线(3)在所垂线上量出或数出与原线段相等的长度(即找到原图关键点的对应点);(4)顺次连接所找到的对应点,即可得到原图形旋转90°后的图形。
5、时钟上包含12大格,60小格,时钟上相邻两数字间即为一大格,一大格为30°;每一大格又平均分为了五个小格,一小格为6°三、平移1、定义:指在一个平面内,将一个图形上的所有点都按照某个方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。
2、性质:平移不改变图形的形状和大小。
3、图形平移的步骤:(1)确定原图形位置、平移的方向、平移的距离。
(2)找出原图形的各关键点。
(3)根据题目要求将各个点依次平移,找出各个点的对应点。
(4)顺次连接平移后的各点。
◆习题:1、图形的变换包括:、、。
其中只是改变原图形位置的变换是、。
2、如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这样的图形就叫()图形,那条直线就是()。
人教版小学数学五年级下册1-7单元各单元知识点思维导图
五下第二单元因数与倍数因数与倍数2,3,5的倍数特征质数和合数含义:因数倍数找因数的方法表示因数A.列乘法算式B.列除法算式A.列举法B.集合法找倍数的方法表示倍数因数的特征倍数的特征如果a÷b=c(a,b,c是非0自然数),那么a是b,c的倍数,b,c是a的因数。
A.一个数的因数是有限的B.最小的因数是1,最大的因数是本身A.列乘法算式B.列除法算式A.列举法B.集合法A.一个数的倍数是无限的B.最小的倍数是本身,没有最大的倍数2的倍数特征5的倍数特征3的倍数特征A.末位是0,2,4,6,8的数都是2的倍数B.奇数与偶数偶数是2的倍数(包括0)奇数不是2的倍数末位是0或5的数都是5的倍数各个数位数字之和是3的倍数质数合数1既不是质数也不是合数A.一个数除了1和它本身没有其他因数一个数除了1和它本身还有其他因数B.最小的质数是2C.100以内的质数2357和11,13后面是17,19,23,29;31,37,41;43,47,53;59,61,6771,73,79;83,89,97奇偶性探究五下第三单元长方体和正方体1.长方体和正方体的认识2.长方体和正方体的表面积3.长方体和正方体体积棱长之和A.长方体:4x(长+宽+高)B.正方体:12x棱长长方体的侧面展开图(1)长方体(2)正方体(长x宽+长x高+宽x高)x26x棱长x棱长2x(ab+ah+bh)(1)体积含义:物体所占的空间大小(2)体积单位:立方厘米,立方分米,立方米(3)体积计算公式A.长方体B.正方体长x宽x高棱长x棱长x棱长abh4.容积和容积单位5.求不规则物体的体积(1)含义:容器所能容纳物体的体积(2)容积单位:升L,毫升ml(3)进率:1L=1000ml1L=1立方分米1ml=1立方厘米底面积x高底面积x高(1)等积变形法(2)排水法把不规则的物体转变成规则的计算排水的体积正方体的侧面展开图平方数的总结人教版小数五下第四单元分数的意义和性质1.分数的意义2.真分数和假分数3.分数的基本性质4.约分5.通分6.分数与小数的互化(1)单位“1”的意义(2)分数的意义一些物体可以看成一个整体A.把单位“1”平均分成若干份,表示其中的一份,或者几份。
人教版五年级下册数学1—4章知识归纳

3.3长方体和正方体的体积
1.体积的意义:物体所占空间的大小叫做物体的体积。
2.体积单位:立方米,立方分米,立方厘米;用字母表示为m3,dm3,cm3。
3.体积单位间的进率:1m3=1000dm31dm3=1000cm3
4.长方体和正方体体积计算公式:
1.2旋转
1.旋转的意义:物体绕着某一点或轴运动,这种运动现象叫做旋转。
2.图形旋转的方向:钟表指针的运动方向是顺时针方向;与钟表上指针的运动方向相反的方向是逆时针方向。
3.图形旋转的性质:图形绕着某一点旋转一定的度数,图形中的对应点、对应线段都旋转相应的度数,对应点到旋转点的距离相等,对应角相等。
2.把单位“1”平均分成若干份,表示其中一份的数叫分数单位。如1的分数单位是.
3.把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数。
4.分数与除法的关系:被除数÷除数=。用字母表示为a÷b =(b≠0)。当分母为0时,分数无意义。
4.2真分数和假分数
1.分子比分母小的分数叫做真分数。真分数都小于1.分子比分母大或分子和分母相等的分数叫做假分数。假分数都大于或等于1.像1,1,…这样的分数叫做带分数。带分数都是由整数部分和分数部分组成的,带分数都比1大。假分数和带分数都一定大于真分数。
长方体的体积=长×宽×高,用字母表示为S=abh
正方体的体积=棱长×棱长×棱长,用字母表示为S=a3。(其中a3读作a的立方,表示3个a相乘。)
长方体(或正方体)的体积=底面积×高,用字母表示为V=Sh
5.容积的意义:容器所能容纳物体的体积,通常叫做它们的容积。
6.容积的计算方法:长方体、正方体等规则容器容积的计算方法和体积的计算方法相同,但是要从容器里面测量长、宽、高。
人教版五年级数学下册知识点整理

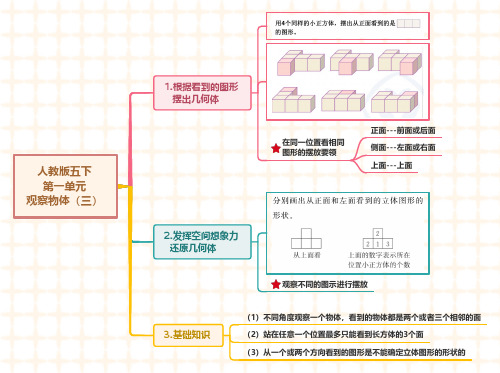
人教版五年级数学下册知识点整理一、观察物体(三)1. 从不同方向观察一个立体图形。
- 就像我们看一个神秘的盒子,从前面看、上面看、左面看,看到的形状可能都不一样哦。
比如说一个由小正方体搭成的立体图形,从前面看可能是一排小正方形,从上面看可能是几排小正方形组成的一个大形状,从左面看又可能是另外一种排列的小正方形啦。
- 而且根据从不同方向看到的形状图,我们要能还原出这个立体图形可能的样子。
这就像玩拼图游戏,不过是用小正方体来拼。
有时候答案不是唯一的,就像有好几种搭小正方体的方法都能得到相同的观察结果呢。
二、因数与倍数。
1. 因数和倍数的概念。
- 因数和倍数就像一对好朋友。
如果整数a除以整数b(b≠0)的商正好是整数而没有余数,我们就说b是a的因数,a是b的倍数。
比如说6÷2 = 3,没有余数,那么2就是6的因数,6就是2的倍数。
而且一个数的因数是有限的,就像一个小圈子里的朋友,而一个数的倍数是无限的,就像有无数个远方的伙伴在等着它呢。
2. 2、3、5的倍数特征。
- 2的倍数特征很好记,个位上是0、2、4、6、8的数就是2的倍数,这些数看起来都很“双数”的感觉。
- 5的倍数特征呢,个位上是0或者5的数就是5的倍数,就像5元、10元的人民币面额一样,个位不是0就是5。
- 3的倍数特征有点特别。
一个数各位上的数字之和是3的倍数,这个数就是3的倍数。
比如说123,1+2 + 3=6,6是3的倍数,所以123也是3的倍数。
3. 质数和合数。
- 质数就像孤独的侠客,只有1和它本身两个因数。
像2、3、5、7这些数,它们只跟1和自己玩。
合数就不一样啦,合数是除了1和它本身还有别的因数的数,就像一个热闹的小团体,有很多小伙伴。
1既不是质数也不是合数,它就像一个特殊的存在,不属于这两个帮派。
三、长方体和正方体。
1. 长方体和正方体的认识。
- 长方体就像一个长长的盒子,它有6个面,每个面都是长方形(特殊情况下有两个相对的面是正方形)。
人教版小学五年级(下册)数学知识点总结大全

人教版小学五年级(下册)数学知识点总结大全一、图形的变换1、轴对称图形:把一个图形沿着某一条直线对折,两边能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
2、成轴对称图形的特征和性质:①对称点到对称轴的距离相等;②对称点的连线与对称轴垂直;③对称轴两边的图形大小形状完全相同。
3、物体旋转时应抓住三点:①旋转中心;②旋转方向;③旋转角度。
旋转只改变物体的位置,不改变物体的形状、大小。
二、因数与倍数1、因数和倍数:如果整数a能被b整除,那么a就是b的倍数,b就是a 的因数。
2、一个数的因数的求法:一个数的因数的个数是有限的,最小的是1,最大的是它本身,方法是成对地按顺序找。
3、一个数的倍数的求法:一个数的倍数的个数是无限的,最小的是它本身,没有最大的,方法时依次乘以自然数。
4、2、5、3的倍数的特征:个位上是0、2、4、6、8的数,都是2的倍数。
个位上是0或5的数,是5的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
5、偶数与奇数:是2倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇数。
6、质数和和合数:一个数,如果只有1和它本身两个因数的数叫做质数(或素数),最小的质数是2。
一个数,如果除了1和它本身还有别的因数的数叫做合数,最小的合数是4。
三、长方体和正方体1、长方体和正方体的特征:长方体有6个面,每个面都是长方形(特殊的有一组对面是正方形),相对的面完全相同;有12条棱,相对的棱平行且相等;有8个顶点。
正方形有6个面,每个面都是正方形,所有的面都完全相同;有12条棱,所有的棱都相等;有8个顶点。
2、长、宽、高:相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3、长方体的棱长总和=(长+宽+高)×4正方体的棱长总和=棱长×124、表面积:长方体或正方体6个面的总面积叫做它的表面积。
5、长方体的表面积=(长×宽+长×高+宽×高)×2S=(ab+ah+bh)×2正方体的表面积=棱长×棱长×6用字母表示:S=6、表面积单位:平方厘米、平方分米、平方米相邻单位的进率为1007、体积:物体所占空间的大小叫做物体的体积。
人教版五年级下册数学第二单元知识点总结

人教版五年级下册数学第二单元知识点总结第一、倍数与因数的关系【知识点1】倍数与因数之间的关系是相互的,不能单独存在。
例如:6是倍数、3和2是因数。
【×】改正:6是3和2的倍数,3和2是6的因数。
练习:【1】8×5=40,【】和【】是【】的因数,【】是【】和【】的倍数。
【2】因为36÷9=4,所以【】是【】和【】的倍数,【】和【】是【】的因数。
【3】在18÷6=3中,18是6的【】,3和6是【】的【】。
【4】在14÷7=2中,【】能被【】整除,【】能整除【】,【】是【】的倍数,【】是【】的因数。
【5】若A÷B=C【A、B、C都是非零自然数】,则A是B的【】数,B是A的【】数。
【6】如果A、B是两个整数【B≠0】,且A÷B=2,那么A是B的,B是A的。
【7】判断并改正:因为7×6=42,所以42是倍数,7是因数。
【】因为15÷5=3,所以15和5是3的因数,5和3是15的倍数。
【】5是因数,15是倍数。
【】甲数除以乙数,商是15,那么甲数一定是乙数的倍数。
【】【8】甲数×3=乙数,乙数是甲数的【】。
A、倍数B、因数C、自然数【知识点2】倍数因数只考虑正数,小数、分数等不讨论倍数、因数的问题。
例如:0.6×5=3,虽然可以表示0.6的5倍是3但是,0.6是小数是不讨论倍数因数问题。
因此类似的:因为0.6×5=3,所以3是0.6和5的倍数。
是错误的说法。
练习:【1】有5÷2=2.5可知【】A、5能被2除尽B、2能被5整除C、5能被2整除D、2是5的因数,5是2的倍数【2】36÷5=7……1可知【】A、5和7是36的因数B、5能整除36C、36能被5除尽D、36是5的倍数【3】属于因数和倍数关系的等式是【】A、2×0.25=0.5B、2×25=50C、2×0=0【知识点3】没有前提条件确定倍数与因数例如:36的因数有【】。
人教版五年级下册数学复习知识要点整理

一图形的变换1、轴对称:把一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(考点,判断一个图形是否是轴对称图形)2、轴对称图形的特点:①对应点在对称轴的两边②对应点到对称轴的距离相等(考点:画对称轴,注意用尺画虚线;画一个图形的轴对称图形,注意根据对应点到对称轴的距离相等,先找对应点,再连线。
例题见书本P4 例2)3、旋转:在平面内,一个图形绕着一个顶点或轴的运动叫做旋转。
(考点:钟面上指针的旋转;画一个图形的旋转后的图形。
注意,找到中心点,看清题意要求顺时针还是逆时针,钟面上一大格是30度,画图时找3、6、9、12时四个时刻的指针方向的边。
例题见书本P5 例3 例4)4、平移:一个图形沿着一条直线的运动称为平移。
二因数和倍数1、3×7=21,3和7是21的因数,21是3和7的倍数,不能说谁是倍数,谁是因数.2、一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
3、一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
4、自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
最小的奇数是1,最小的偶数是0。
任何一个自然数,不是奇数,就是偶数。
5、个位上是0,2,4,6,8的数都是2的倍数.6、个位上是0或5的数,是5的倍数。
7、一个数各位上的数的和是3的倍数,这个数就是3的倍数。
8、个位上是0的数既是2的倍数,又是5的倍数。
9、能同时被2、3、5整除(同时有因数2、3、5)的最小数是30,最大的两位数是90,最小的三位数是120.10、100以内的质数:二三五七和十一,(2、3、5、7、11)十三后面是十七,(13、17)还有十九别忘记,(19)二三九, 三一七,(23、29、31、四一,四三,四十七,(41、43、47)五三九, 六一七, (53、59、61、67)七一,七三,七十九, (71、73、79)八三,八九,九十七。
人教版数学五年级下册第六单元《分数的加法和减法》-知识点整理

分数的加法和减法二、知识要点1、分数数的加法和减法(1)同分母分数加、减法(分母不变,分子相加减)(2)异分母分数加、减法(通分后再加减)(3)分数加减混合运算:同整数。
(4)结果要是最简分数2、带分数加减法:带分数相加减,整数部分和分数部分分别相加减,再把所得的结果合并起来。
3、详细解释(1)同分母分数加、减法①、同分母分数加、减法:同分母分数相加、减,分母不变,只把分子相加减。
②、计算的结果,能约分的要约成最简分数。
例:分析:在同分母相加减中,一定要注意分母不变,分子相加减,上面两题计算步骤正确。
(2)异分母分数加、减法①、分母不同,也就是分数单位不同,不能直接相加、减。
②、异分母分数的加减法:异分母分数相加、减,要先通分,再按照同分母分数加减法的方法进行计算。
例:通分整数的加减运算分数的加法和减法同分母分数的加减法(分数单位相同)异分母分数的加减法(分数单位不同)分数的加减法混合运算最小公倍数整数加法的运算定律分数单位相同的数能相加减分析:异分母相加减时,我们一定要先找到最小公分母通分,然后根据同分母的计算方法来计算。
(3)分数加减混合运算①、分数加减混合运算的运算顺序与整数加减混合运算的顺序相同。
在一个算式中,如果有括号,应先算括号里面的,再算括号外面的;如果只含有同一级运算,应从左到右依次计算。
②、整数加法的交换律、结合律对分数加法同样适用。
例:分析:第一个题:有三个分数,那么我们可以选择先通分两个分数,然后再通分第三个分数,也就是解法1的作法。
我们还可以选择三通分数同时同分,当然公分母可能既要复杂一些,但是和找两个分数的公分母方法是一样的。
第二个题:有括号,在四则运算中我们知道有括号的先算括号内,记住:整数的计算法则在分数中照样有效。
三、经验之谈:分数的计算顺序和整数的运算顺序是相同的,异分母分数相加中在找最小公倍数时我们要细心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识链接
(一)分数的起源、形成与发展
我们知道,单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。
分母表示把一个物体平均分成几份,分子表示取了其中的几份。
分子在上分母在下,也可以把它当做除法来看,用分子除以分母(因0在除法不能做除数,所以分母不能为0(例10/0,表示把单位“1”平均分0份,取10份,完全没有意义))相反除法也可以改为用分数表示。
然而,说分数的历史,得从3000多年前的埃及说起。
3000多年前,古埃及为了在不能分得整数的情况下表示数,用特殊符号表示分子为1的分数。
2000多年前,中国有了分数,但是,秦汉时期的分数的表现形式不一样。
印度出现了和我国相似的分数表示法。
再往后,阿拉伯人发明了分数线,今天分数的表示法就由此而来。
200多年前,瑞士数学家欧拉,在《通用算术》一书中说,要想把7米长的一根绳子分成三等份是不可能的,因为找不到一个合适的数来表示它。
如果我们把它分成三等份,每份是7/3米。
像7/3就是一种新的数,我们把它叫做分数。
为什么叫它分数呢?分数这个名称直观而生动地表示这种数的特征。
例如,一个西瓜四个人平均分,不把它分成相等的四块行吗?从这个例子就可以看出,分数是度量和数学本身的需要--除法运算的需要而产生的。
最早使用分数的国家是中国。
我国古代有许多关于分数的记载。
在《左传》一书中记载,春秋时代,诸侯的城池,最大不能超过周国的1/ 3,中等的不得超过1/5 ,小的不得超过1/9。
秦始皇时期,拟定了一年的天数为365又1/4天。
《九章算术》是我国1800多年前的一本数学专著,其中第一章《方田》里就讲了分数四则算法。
在古代,中国使用分数比其他国家要早出一千多年。
所以说中国有着悠久的历史,多么灿烂的分数的文化啊!
(二)分数的产生
人类历史上最早产生的数是自然数(非负整数),以后在度量和平均分时往往不能正好得到整数的结果,这样就产生了分数。
用一个作标准的量(度量单位)去度量另一个量,只有当量若干次正好量尽的时候,才可以用一个整数来表示度量的结果。
如果量若干次不能正好量尽,有两种情况:
例如,用b作标准去量a:
一种情况是把b分成n等份,用其中的一份作为新的度量单位去度量a,量m次正好量尽,就表示a含有把b分成n等份以后的m个等份。
例如,把b分成4等份,用其中的一份去量a,量9次正好量尽。
在这种情况下,不能用一个整数表示用b去度量a的结果,就必须引进一种新的数--分数来表示度量的结果。
另一种情况是无论把b分成几等份,用其中的一份作为新的度量a,都不能恰好量尽(如用圆的直径去量同一圆的周长)。
在这种情况下,就需要引进一种新的数-无理数。
在整数除法中,两个数相除,有时不能得到整数商。
为了使除法运算总可以施行,也需要引进新的一种数-分数。
综上所述,分数是在实际度量和均分中产生的。
