教师用习题解答第5章
第5章 习题解答
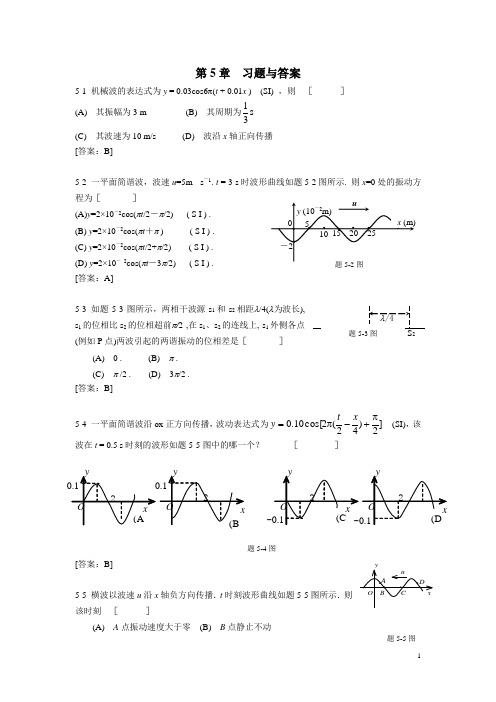
第5章 习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则[ ] (A) 其振幅为3 m(B) 其周期为s 31(C) 其波速为10 m/s (D)波沿x 轴正向传播 [答案:B]5-2 一平面简谐波,波速u =5m · s -1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为[ ](A)y =2×10-2cos(πt /2-π/2) ( S I ) . (B) y =2×10-2cos(πt +π ) ( S I ) . (C) y =2×10-2cos(πt /2+π/2) ( S I ) .(D) y =2×10- 2cos(πt -3π/2) ( S I ) .[答案:A]5-3 如题5-3图所示,两相干波源s 1和s 2相距λ/4(λ为波长), s 1的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是[ ](A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案:B]5-4 一平面简谐波沿ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个? [ ][答案:B]5-5 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如题5-5图所示.则该时刻 [ ](A) A 点振动速度大于零 (B) B 点静止不动ux (m)y (10-2m)· · · · · · · 0 51015 20 25 -2题5-2图题5-4图题5-5图-(C) C 点向下运动 (D) D 点振动速度小于零 [答案:D]5-6 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形如题5-6图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是[ ][答案:A]5-7 一简谐波沿x 轴正方向传播,t = T /4时的波形曲线如题5-7图所示.若振动以余弦函数表示,且此题各点振动的初相取-π 到π 之间的值,则 [ ] (A) O 点的初相为00=φ(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ [答案:D]5-8 在驻波中,两个相邻波节间各质点的振动[ ](A) 振幅相同,相位相同 (B) 振幅不同,相位相同 (C) 振幅相同,相位不同 (D) 振幅不同,相位不同 [答案:B]5-9 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:[ ](A) 它的动能转化为势能. (B) 它的势能转化为动能.(C) 它从相邻的一段质元获得能量其能量逐渐增大. (D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小. [答案:D]ωS A O ′ωSA O ′ωωSAO ′(A)(B)(C)(D)S题5-6图5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是__________,波长是__________,频率是__________,波的传播速度是__________。
幼儿教育学习题第五章 幼儿园环境

幼儿教育学习题第五章幼儿园环境一、单项选择题1.环境分为物质环境和( )。
A.社会环境B.精神环境C.城市环境D.局部环境2.物质环境是学前教育存在与发展的( )。
A.必备条件B.主要条件C.次要条件D.生活条件6.创设幼儿园环境时应考虑不同地区、不同条件幼儿园的实际情况,因地制宜,这体现了( )原则。
A.开放性B.经济性C.发展适宜性D.参与性二、名词解释1.精神环境2.物质环境3.环境的界限性4.环境的相容性5.环境的转换性6.幼儿常规三、判断题1.幼儿园环境所具有的教育性与可控性是相互独立的。
2.参与性原则就是环境创设过程中幼儿与教师需要共同参与整个过程。
3.环境创设中的开放性原则就是幼儿园要多搞活动,让外界多参与幼儿园的各种建设。
4.教师要尽量让幼儿感受到环境是由幼儿自己决定的。
5.在调整环境的时候,教师只需要考虑教学内容的变化,而不是环境的发展性和教育四、简答题1.什么叫幼儿园环境?2.什么叫发展适宜性原则?如何具体体现这一原则?3.幼儿园内环境的特点表现在哪些方面?4.影响幼儿园内环境质量的重要因素有哪些?5.如何理解幼儿园环境创设的经济性原则?6.如何理解幼儿园环境创设的参与性原则?7.如何理解幼儿园环境创设的开放性原则?8.运用环境体验法应注意的事项是什么?五、论述题1.为了发挥幼儿园环境的作用,创设时需要考虑哪些原则?2.教师在幼儿园环境创设中的作用是什么?3.在幼儿园环境创设中存在的误区是什么?六、案例分析幼儿园可设置的活动区有:社会活动区(娃娃家、医院、市场、马路等);自然科学活动区(天文、地理、生物、化学、物理等自然事物和现象的观察、实验等);数学活动区;艺术活动区(音乐、美术等);语言活动区(阅读、故事表演等);建构操作区(拼、插、搭、小制作等);室外可有玩沙区、玩水区、种植区、饲养区等。
这种划分并不固定,每个幼儿园在具体操作时可视情况化整为零、灵活搭配。
场地大一些的,可设置大的活动区;场地比较小的,可设置小一点的活动角,如图书角、数学角、自然角、娃娃家等。
第5章习题解答

第5章习题解答1. 解:Q235钢,m l 5.5=荷载标准值:m kN q k /5.34245.10=+= 荷载设计值:m kN q /2.46244.15.102.1=⨯+⨯=弯矩设计值:m kN ql M x ⋅=⨯⨯==69.1745.52.46818122(1)假定梁的受压翼缘设置可靠的侧向支承,可以保证梁的整体稳定由抗弯强度要求的截面模量为:3361082.77321505.11069.174mm f M W x x nx ⨯=⨯⨯==γ查型钢表选用I36a ,截面几何特性:3878cm W x =,415796cm I x =,质量m kg q /0.60= 强度验算:22326/215/44.1921087805.18/55002.16.01069.174mm N f mm N W M nx x x =<=⨯⨯⨯⨯+⨯=γ 满足要求。
挠度验算:[]2501428110157961006.25500)6.05.34(384538454533=<=⨯⨯⨯⨯+⨯=⋅=l EI l q l x kx υυ满足要求。
故选用此截面。
(2)假定梁的受压翼缘无可靠的侧向支承按整体稳定确定梁截面假定工字钢型号在I45~I63之间,均布荷载作用在梁上翼缘,自由长度m l 5.51=,由附表3-2查政体稳定系数6.0660.0>=b ϕ,所以643.0660.0282.007.1282.007.1=-=-='bbϕϕ所需毛截面抵抗矩:3361063.1263215643.01069.174mm f M W b x nx ⨯=⨯⨯='=ϕ查型钢表选用I45a ,截面几何特性:31433cm W x =,432241cm I x =,质量m kg q /4.80=强度验算:22326/215/52.11810143305.18/55002.1804.01069.174mm N f mm N W M nx x x =<=⨯⨯⨯⨯+⨯=γ满足要求。
幼儿教育学习题第五章幼儿园环境

幼儿教育学习题第五章幼儿园环境一、单项选择题1.环境分为物质环境和 ( )。
A .社会环境B .精神环境C.城市环境D.局部环境2.物质环境是学前教育存在与发展的( )。
A .必备条件B .主要条件C.次要条件D.生活条件6.创设幼儿园环境时应考虑不同地区、不同条件幼儿园的实际情况,因地制宜,这体现了( ) 原则。
A .开放性B.经济性C.发展适宜性D.参与性二、名词解释1.精神环境2.物质环境3.环境的界限性4.环境的相容性5.环境的转换性6.幼儿常规三、判断题1.幼儿园环境所具有的教育性与可控性是相互独立的。
2.参与性原则就是环境创设过程中幼儿与教师需要共同参与整个过程。
3.环境创设中的开放性原则就是幼儿园要多搞活动,让外界多参与幼儿园的各种建设。
4.教师要尽量让幼儿感受到环境是由幼儿自己决定的。
5.在调整环境的时候,教师只需要考虑教学内容的变化,而不是环境的发展性和教育四、简答题1.什么叫幼儿园环境?2.什么叫发展适宜性原则?如何具体体现这一原则?3.幼儿园内环境的特点表现在哪些方面?4.影响幼儿园内环境质量的重要因素有哪些?5.如何理解幼儿园环境创设的经济性原则?6.如何理解幼儿园环境创设的参与性原则?7.如何理解幼儿园环境创设的开放性原则?8.运用环境体验法应注意的事项是什么?五、论述题1.为了发挥幼儿园环境的作用,创设时需要考虑哪些原则?2.教师在幼儿园环境创设中的作用是什么?3.在幼儿园环境创设中存在的误区是什么?六、案例分析幼儿园可设置的活动区有:社会活动区(娃娃家、医院、市场、马路等 );自然科学活动区 (天文、地理、生物、化学、物理等自然事物和现象的观察、实验等);数学活动区;艺术活动区( 音乐、美术等 );语言活动区 (阅读、故事表演等 );建构操作区 (拼、插、搭、小制作等);室外可有玩沙区、玩水区、种植区、饲养区等。
这种划分并不固定,每个幼儿园在具体操作时可视情况化整为零、灵活搭配。
第5章习题解答

如果按指令执行周期结束(25μs)响应DMA请求,必然会 造成数据丢失;因此必须按每个机器周期结束响应DMA 请 求的方案。
解:打印机的打印动作只受打印机本身控制, 与CPU 无关,因此打印机正在打印时,虽然 有优先级别更高的磁盘请求中断,打印机也 不会停止打印。而如果CPU 正在执行打印机 的中断服务程序,即打印机正在接收数据, 此时若磁盘请求中断,CPU 就要中断正在运 行的打印机中断服务程序。
5.33 试从下面7个方面比较程序查询、程 序中断和DMA三种方式的综合性能。
程序查询方式 中断方式
DMA 方式
软件
软件
硬件
字
字
数据块
串行
宏观并行,微观串行
CPU主动查询
主动/被动
慢 最经济
最慢 经济
中低速实时处理设备 中低速I/5.19 在程序中断方式中,磁盘申请中断的优先权高于 打印机。当打印机正在进行打印时,磁盘申请中断,试 问是否要将打印机输出停下来,等磁盘操作结束后,打 印机输出才能继续进行?为什么?
例5.32 设磁盘存储器转速为3000 转/分,分8 个扇区,每扇区 存储1K 字节,主存与磁盘存储器传送的宽度为16 位。假设一 条指令最长执行时间是25μs ,是否可采用一条指令执行结束时 响应DMA 请求的方案,为什么?若不行,应采取什么方案?
解: 磁盘的数据传输速率=每一磁道容量×转速 = 1×8×50×3000/60
作业
❖ 5.2、5.10、 5.12、5.13、 ❖ 5.18、 5.29、5.32、5.33 ❖ 思考题 5.25
【课程练习】习题解答-第五章 详细设计

第五章详细设计1.详细设计的基本任务是什么?有哪几种描述方法?详细设计的基本任务:(1)为每个模块进行详细的算法设计。
(2)为每个模块内的数据结构进行设计。
(3)对数据库进行设计,即确定数据库的物理结构。
(4)其他设计:a.代码设计b.输入/输出格式设计。
c.人机对话设计。
(5)编写详细设计说明书。
(6)评审。
描述方法(三种):a.程序流程图b.PAD图 C.过程设计语言2.结构化程序设计基本要求要点是什么?a.采用自顶向下、逐步求精的程序设计方法b.使用三种基本程序控制结构构造程序1).用顺序方式对过程分解,确定各部分的执行顺序。
2).用选择方式对过程分解,确定某个部分的执行条件。
3).用循环方式对过程分解,确定某个部分重复的开始和结束的条件。
c.主程序员组的组织形式。
3.简述Jackson 方法的设计步骤。
Jsp 方法一般通过以下5个步骤来完成设计:a.分析并确定输入/出数据的逻辑结构,并用Jackson 结构图表示这些数据结构。
b.找出输入数据结构和输出数据结构中有对应关系的数据单元。
c.按一定的规则由输入、输出的数据结构导出程序结构。
d.列出基本操作与条件,并把它们分配到程序结构图的适当位置。
e.用伪码写出程序。
4.请使用流程图、PAD图各PDL语言描述下列程序的算法。
(1)在数据A(1)-A(10)中求最大数和次大数。
(2)输入三个正整数作为边长、判断该三条边构成的三角形是等边、等腰或一般三角形。
答:(1)1)流程图:2)PAD图3)PDL语言定义n1=n2=0输入A(1).......A(10)n1=n2=A(1)while i>10if A(i)>=n1n2=n1n1=A(i)end while5.用PAD图描述下面问题的控制结构。
有一个表A(1)、A(2)、........A(n),按递增顺序排列。
给定一个Keyw值,在表中用折半查找。
若找到将表位置i送入x,否则将零送到x,同时将Key值插入表中。
范钦珊版材料力学习题全解 第5章 梁的弯曲问题(1)-剪力图与弯矩图

M A = ql 2
| FQ | max = 5 ql 4
| M | max = ql 2
题(c)
∑ F y = 0 , FRA = ql (↑)
9
∑ M A = 0 , M A = ql 2
∑ M D = 0 , ql 2 + ql ⋅ l − ql ⋅ − M D = 0
3 2 ql 2 | FQ | max = ql MD =
C
4000 4000
B
FB
习题 5-8 载荷图之二
5-9 试作图示刚架的剪力图和弯矩图,并确定 FQ
max
、 M
max
12
习题 5-9 图
解:题(a) :
∑M A = 0
FRB ⋅ 2l − FP ⋅ l − FP ⋅ l = 0
FRB = FP (↑)
∑ F y = 0 , F Ay = FP (↓)
∑ Fx = 0 , FAx = FP (←)
C
2
1
B
C
-
B
1
D
M(FPl)
1 +
D
FQ(FP)
A
A
习题 5-9a 的弯矩图
剪力图和弯矩图如图所示,其中 | M | max = 2 FP l , 位于刚节点 C 截面;
| FQ |max = FP
题(b) : ∑ F y = 0 , F Ay = ql (↑)
8
习题 5-6c、e 解图
习题 5-6d、f 解图
题(b)
∑ M A = 0 − ql 2 − ql ⋅ l + ql ⋅ l + FRB ⋅ 2l = 0
2
FRB
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思 考 题5.1 当热力学系统处于非平衡态时,温度的概念是否适用? 答:温度的概念是指处在同一热平衡状态下的所有热力学系统,在宏观上都具有的一种共同的物理性质。
所以在非平衡态时温度的概念不适用。
5.2 内能和热量的概念有何不同?下面两种说法是否正确? (1)物体的温度愈高,则热量愈多; (2)物体的温度愈高,则内能愈大。
答:内能指物体内所有分子作无规则运动时,分子动能和分子势能的总和。
热量是在热传导方式下物体之间所交换能量的计量。
所以(1)的说法不正确;(2)的说法正确。
5.3 什么是热力学系统的平衡态?气体在平衡态时有何特征?当气体处于平衡态时还有分子热运动吗?答:不受外界影响的条件下宏观性质处于不随时间改变的系统状态叫做平衡态...。
气体处于平衡态时,整个系统热平衡(各部分温度相等);力平衡(各部分压强相等);化学平衡和相平衡(浓度均匀,组成不随时间变化)。
分子热运动始终存在。
5.4 试说明为什么气体热容的数值可以有无穷多个?什么情况下气体的热容为零?什么情况下气体的热容是无穷大?什么情况下是正值?什么情况下是负值?答:气体热容的大小与气体升温的过程或条件有关。
不同的热力学过程,热容的值都是不同的。
因为变化过程可有无穷多个,所以气体热容的数值可以有无穷多个。
绝热过程热容为零。
等温过程热容为无穷大。
系统温度升高,从外界吸热的热力学过程气体热容为正。
系统温度升高,向外界放出热量的热力学过程气体热容为负。
5.5 有可能对物体加热而不致升高物体的温度吗?有可能不作任何热交换,而使系统的温度发生变化吗?答:气体等温膨胀过程吸收外界热量而温度不变。
存在对系统不作任何热交换而温度发生变化情况,如气体的绝热压缩过程。
5.6 讨论理想气体在下述过程中Q W E 、、∆的正负。
(1)等容降压;(2)等压压缩;(3)绝热膨胀。
答:(1)等容过程做功为零,W 为零。
等容降压时温度下降,所以内能减少,E ∆为负。
由热力学第一定律得Q 为负。
(2)压缩过程系统做负功,W 为负。
等压压缩时温度下降,所以内能减少,E ∆为负。
由热力学第一定律得Q 为负。
(3)绝热过程Q 为零。
膨胀过程系统做正功,W 为正。
由热力学第一定律得E ∆为负。
5.7 有人说,因为在循环过程中系统对外做的净功在数值等于p-V 图中封闭曲线所包围的面积,所以封闭曲线所包围的面积越大,循环效率就越高,对吗?答:不正确,因为循环效率取决于系统对外做的净功和系统由高温热源吸收的热量,只有在从高温热源吸收的热量一定的情况下,封闭曲线所包围的面积越大,即系统对外所做的净功越多,循环效率越高,如果从高温热源吸收的热量不确定,则循环效率不一定越高。
5.8 温度差对于热机的驱动是否是必须的,为什么?答:温度差对于热机的驱动是必须的,因为根据热力学第二定律,热机要不断地把吸取的热量变为有用的功,就不可避免地将一部分热量传给低温热源5.9 夏天将冰箱的门打开,让其中的冷空气出来为室内降温,这种方法可取吗?答:不可取,因为电冰箱是对低温端的利用,它在从低温端吸收热量的同时,还要向高温端放出热量,且放出的热量大于从低温端带走的热量,因此打开冰箱门不仅不能降低室温,相反,会使室温升高。
5.10 判别下列说法是否正确:(1)功可以全部转化为热,但热不能全部转化为功;(2)热量能从高温物体传到低温物体,但不能从低温物体传到高温物体。
答:(1)不正确。
因为气体的等温膨胀过程热就可以全部转化为功(2)不正确。
因为如果外界对气体做功,热量就能从低温物体传到高温物体。
5.11 从原理上讲如何计算在始末状态之间进行不可逆过程所引起的熵变。
答:热力学过程的始末状态之间的熵变与具体的过程无关。
对不可逆过程,可选取相同始末状态的可逆过程来计算熵变。
习 题5.1 一热力学系统由如图所示的状态,a 沿acb 过程到达状态b 时,吸收了560J 的热量,对外做功356J 。
(1)如果它沿adb 过程达到状态b 时,系统对外做功220J ,它吸收了多少热量?(2)当系统由b 状态沿曲线ba 返回状态a 时,外界对系统做功为282J ,试问系统是吸热还是放热?热量传递多少?解: (1)J W Q E E acb acb a b 204356560=-=-=-J W E E Q adb a b adb 424220204=+=+-=(2)JW E E Q bab a ba 486)282(204-=-+-=+-=(负号表示系统对外界放了486J 的热量)5.2 64g 氧气的温度由273K 升至323K,(1)保持体积不变;(2)保持压强不变。
在这两个过程中氧气各吸收了多少热量?各增加了多少内能?对外各做了多少功?解:(1)J T C M Q m V V 3,1008.227332331.8253264⨯=-⨯⨯⨯=∆=)(μJ Q E V 31008.2⨯==∆W=0(2)J T C M Q m p p 3,1091.227332331.82253264⨯=-⨯⨯+⨯=∆=)(μ J Q E V 31008.2⨯==∆J E Q W p 331083.010)08.291.2(⨯=⨯-=∆-=5.3 10g 氦气吸收310J 的热量时压强未发生变化,它原来的温度是300K,最后的温度是多少?解:由)(22)(1212,T T R i M T T C MQ m p p -+=-=μμ,得K RM i Q T T 3191031.8)23(4102300)2(2312=⨯⨯+⨯⨯+=++=μ习题5.1图5.4 如图所示,一定量的空气,开始时在状态A ,其压强为2.0atm ,体积为2L ,沿直线AB 变化到状态B 后,压强变为1.0atm ,体积变为3L,求在此过程中气体所做的功。
解:气体所做功等于过程曲线以下的面积 J W 2351052.110)23(10013.1)12(21⨯=⨯-⨯⨯⨯+⨯=-5.5 一定量氢气在保持压强为a P 51000.4⨯不变的情况下,温度由273K 升高到323K 时,吸收了J 4100.6⨯的热量。
(1)求氢气的量是多少摩尔? (2)求氢气内能变化多少?解:(1)由T R i nT nC Q m p p ∆+=∆=22,,得 mol T R i Q n 3.41)273323(31.8)25(100.62)2(24=-⨯⨯+⨯⨯=∆+=(2)J T R i n E 41029.4)273323(31.8253.412⨯=-⨯⨯⨯=∆=∆5.6 标准状态下的2mol 氢气吸收外界500J 的热量。
(1)若体积不变,问这热量变为什么?氢的温度变为多少?(2)若温度不变,问这热量变为什么?氢的压强和体积各变为多少?解:(1)等容过程不做功,由热力学第一定律,有)()(21212T T iR T T R iM E Q V -=-=∆=μ得K iR Q T T 28531.8550027312=⨯+=+= (2)等温过程内能不变,热量变为气体对外做功。
12ln 21V V RT MV dV RT M W Q V V T T μμ===⎰代入数据,得12ln27331.82500V V ⨯⨯= 116.112=V V 35001205.010013.127331.82116.1116.1116.1m p nRT V V =⨯⨯⨯⨯=== a P V nRT p 5221091.005.027331.82⨯=⨯⨯==习题5.4图5.7 2mol 的理想气体在300K 时,从4L 等温压缩到1L ,试求这气体做的功和吸收的热量。
解:12ln 21V V RT M V dV RT M W V V T μμ==⎰J 691241ln 30031.82-=⨯⨯=J W Q T T 6912-==5.8 一定量的氮气,压强为1atm,体积为10L,温度为300K 。
(1)保持体积不变;(2)保持压强不变。
在温度都升到400K 的过程中,各需吸收多少热量?内能增加多少?对外做功多少?解:(1)T T V p i T R M i T R i M T C M Q m V V ∆=∆=∆=∆=111,222μμμJ 33510844.0100300101010013.125⨯=⨯⨯⨯⨯⨯=- J Q E V 310844.0⨯==∆0=V W(2)T T V p i T R M i T R i M T C M Q m p p ∆+=∆+=∆+=∆=111,222222μμμ J 3351018.1100300101010013.127⨯=⨯⨯⨯⨯⨯=- 因为内能仅是温度的函数,所以本题中两个过程的内能增量相同。
有J E 21044.8⨯=∆J E Q W p p 33310336.010844.01018.1⨯=⨯-⨯=∆-=5.9 一定质量的理想气体,其γ=1.40,若在等压下加热,使其体积增大为原体积的m 倍为止。
试求传给气体的热量中,用于做功与增加内能的热量之比。
解:5,4.1==i 即,所以是双原子分子因γ 等压过程中V 和T 为变量,有T nR V p W p ∆=∆=T R in E ∆=∆25222==∆∆=∆∴i T R in T nR EW p5.10 有1mol 的氧气,温度为300K 时,体积为0.002m3,试计算下列两种过程中氧气所做的功:(1)绝热膨胀到体积为0.023;(2)等温膨胀到体积为0.023解:(1)由绝热过程方程常量=-T V1γ,有111212T V T V --=γγK V V T T 4.119)02.0002.0(300)(14.112112=⨯==--γ JTR in E W Q 31075.3)3004.119(31.8252⨯=-⨯⨯-=∆-=∆-=(2)J V V RT M W T 3121074.5002.002.0ln 30031.81ln ⨯=⨯⨯⨯==μ5.11 一作卡诺循环的热机,高温热源的温度为400K,每一循环从此热源吸进100J 的热量并向一低温热源放出80J 的热量.求(1) 该循环的热机效率; (2) 低温热源温度. 解:(1)%2010080100121=-=-=Q Q Q η (2)对于卡诺热机,其效率为121T T -=η 所以 K K T T 320400%)201()1(12=⨯-=-=η5.12 有一卡诺制冷机,从一温度为-10℃的冷藏室中吸取热量,而向温度为20℃的物体(通常为水)放出热量,设该制冷机所耗功率为15kW ,问每分钟从冷藏室中吸取的热为多少,每分钟放热为多少?解:卡诺制冷机的制冷系数为302632632932632122=-=-==T T T W Q e 所以每分钟从冷藏室中吸收的热量为J J eW Q 6321089.760101530263⨯=⨯⨯⨯== 此时,每分钟向温度为20℃的物体放出的热量为J J W Q Q 656211079.8)1091089.7(⨯=⨯+⨯=+=5.13 一卡诺热机的低温热源温度为7℃,效率为40%,若要将其效率提高到50%,求高温热源的温度需要提高多少?解:卡诺热机的效率为:121T T -=η 可得,K K T T 46740.017273121=-+=-=η K K T T 56050.017273111211=-+=-=η所以 K K T T T 93)467560(11=-=-=∆5.14 一热机在1000K 和300K 之间工作,若(1)高温热源温度提高到1100K ;(2)低温热源温度降低到200K ,求理论上热机效率各增加多少?为了提高热机的效率,那一种方案更好?解:卡诺热机的效率为%7010003001112=-=-=T T η 第一种方案热机的效率为%73110030011121=-=-=T T η 第二种方案热机的效率为2212001180%1000T T η=-=-= 虽然第二种方案的热机效率高,但制冷过程本身就要耗能,所以应选第一种方案。
