计算多遇地震下各层住地震内力(分别用基底剪力法与振型分解法求解)
王社良版《抗震结构设计》要点及重要习题及答案-考试必胜

六、 计算题1、某两层钢筋混凝土框架,集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ,每层层高皆为 4.0m ,各层的层间刚度相同m /kN 863021=∑=∑D D ;Ⅱ类场地,设防烈度为7度,设计基本地震加速度为0.10g ,设计分组为第二组,结构的阻尼比为05.0=ζ。
(1)求结构的自振频率和振型,并验证其主振型的正交性(2)试用振型分解反应谱法计算框架的楼层地震剪力解1):(1)计算刚度矩阵m kN k k k /17260286302111=⨯=+=m kN k k k /863022112-=-==m kN k k /8630222==(2)求自振频率])(4)()[(21211222112121122211122212122,1k k k k m m k m k m k m k m m m --++= ω ])8630(863017260[(1201204)172601208630120()172601208630120[(1201202122--⨯⨯⨯-⨯+⨯⨯+⨯⨯⨯=28.188/47.27=s rad /24.51=ω s rad /72.132=ω(3)求主振型当s rad /24.51=ω 1618.186301726024.5120212112111112=--⨯=-=k k m X X ω 当s rad /72.132=ω1618.086301726072.13120212112212122-=--⨯=-=k k m X X ω (4)验证主振型的正交性质量矩阵的正交性0618.0000.112000120618.1000.1}]{[}{21=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡⎭⎬⎫⎩⎨⎧=T T X m X 刚度矩阵的正交性0618.0000.186308630863017260618.1000.1}]{[}{21=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡--⎭⎬⎫⎩⎨⎧=T T X k X 解2):由表3.2查得:Ⅱ类场地,第二组,T g =0.40s由表3.3查得:7度多遇地震08.0max=α第一自振周期g g T T T T 5s,200.12111<<==ωπ第二自振周期g g T T T T 5s,458.02122<<==ωπ (1)相应于第一振型自振周期1T 的地震影响系数: 030.008.0200.140.09.0max 9.011=⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ααT T g第一振型参与系数 724.0618.11200000.11200618.11200000.11200222121111=⨯+⨯⨯+⨯==∑∑==i i i n i i i m m φφγ 于是:kN 06.261200000.1724.0030.01111111=⨯⨯⨯==G F φγαkN 17.421200618.1724.0030.02121112=⨯⨯⨯==G F φγα第一振型的层间剪力:kN 17.421212==F VkN 23.68121111=+=F F V(2)相应于第二振型自振周期2T 的地震影响系数: 071.008.0458.040.09.0max 9.022=⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ααT T g第二振型参与系数 276.0)618.0(1200000.11200)618.0(1200000.11200222122122=-⨯+⨯-⨯+⨯==∑∑==i i in i ii m m φφγ 于是:kN 52.231200000.1276.0071.01212221=⨯⨯⨯==G F φγαkN 53.141200)618.0(276.0071.02222222-=⨯-⨯⨯==G F φγα第二振型的层间剪力:kN 53.142222-==F VkN 99.8222121=+=F F V(3)由SRSS 法,计算各楼层地震剪力: kN 60.44)53.14(17.422222222=-+==∑=j j V V kN 821.6899.823.682222211=+==∑=j j VV2、某两层钢筋混凝土框架,集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ,每层层高皆为4.0m ,框架的自振周期s 028.11=T ;各层的层间刚度相同m /kN 863021=∑=∑D D ;Ⅱ类场地,7度第二组()08.0 s,40.0max ==αg T ,结构的阻尼比为05.0=ζ,试按底部剪力法计算框架的楼层地震剪力,并验算弹性层间位移是否满足要求([]450/1=e θ)。
例题-底部剪力法

m2 270t m1 270t
K 2 195 MN/m K1 245 MN/m
解: (1)计算结构等效总重力荷载代表值 Geq 5997 .6kN (2)计算水平地震影响系数 特征周期值(s)
max 0.16 Tg 0.4s
Tg T1 3s T 1 ( g ) 2 max T
333 .5 333 .5 166 .7
m2 270t m1 270t
333 .5 667 .0 833 .7
例2:六层砖混住宅楼,建造于基本烈度为8度 区,场地为Ⅱ类,设计地震分组为第一组,根 据各层楼板、墙的尺寸等得到恒荷和各楼面活 荷乘以组合值系数,得到的各层的重力荷载代 表值为G1=5399.7kN, G2=G3=G4=G5=5085kN, G6=3856.9kN。试用底部剪力法计算各层地震剪 力标准值。
例2:基本烈度为8度,场地为Ⅱ类,设计地震分 组为第一组,G1=5399.7kN, G2=G3=G4=G5=5085kN, G6=3856.9kN。计算各层地震剪力标准值。 解: 结构总水平地震作用标准值
地震影响系数最大值(阻尼比为0.05)
G6 G5 G4 G3 G2 G1
2.70 2.70 2.70 2.70 2.70 2.95
(3)计算结构总的水平地震作用标准值
(4)顶部附加水平地震作用
Fn n FEK
FEK 833 .7kN
T1 1.4Tg T1 1.4Tg
顶部附加地震作用系数
Tg ( s )
1.4Tg 0.56
T1 1.4Tg
n 0
0.08T1 0.07 0.35 ~ 0.55 0.08T1 0.01
m3 180t
1、《抗震规范》给出的设计反应谱中,当结构自振周期在0.1s~Tg之间时,谱曲线为( A )

1、《抗震规范》给出的设计反应谱中,当结构自振周期在0.1s~Tg之间时,谱曲线为(A )A.水平直线 B.斜直线 C.抛物线 D.指数曲线2、实际地震烈度与下列何种因素有关?( B )A.建筑物类型B.离震中的距离C.行政区划D.城市大小3、规范规定不考虑扭转影响时,用什么方法进行水平地震作用效应组合的计算?( B )A.完全二次项组合法(CQC法)B. 平方和开平方法(SRSS法)C.杜哈米积分D. 振型分解反应谱法4、基底剪力法计算水平地震作用可用于下列何种建筑? ( C )A.40米以上的高层建筑B.自振周期T1很长(T1>4s)的高层建筑C. 垂直方向质量、刚度分布均匀的多层建筑D. 平面上质量、刚度有较大偏心的多高层建筑5、地震系数k与下列何种因素有关?( A )A.地震基本烈度B.场地卓越周期C.场地土类别D.结构基本周期6、9度区的高层住宅竖向地震作用计算时,结构等效总重力荷载G eq为(C )A. 0.85(1.2恒载标准值G K+1.4活载标准值Q K)B. 0.85(G K+Q k)C. 0.75(G K+0.5Q K)D. 0.85(G K+0.5Q K)7、框架结构考虑填充墙刚度时,T1与水平弹性地震作用F e有何变化?( A )A.T1↓,F e↑B.T1↑,F e↑C.T1↑,F e↓D.T1↓,F e↓8、抗震设防区框架结构布置时,梁中线与柱中线之间的偏心距不宜大于( A )A.柱宽的1/4 B.柱宽的1/8 C.梁宽的1/4 D.梁宽的1/89、土质条件对地震反应谱的影响很大,土质越松软,加速度谱曲线表现为( A )A.谱曲线峰值右移B.谱曲线峰值左移C.谱曲线峰值增大D.谱曲线峰值降低10、震中距对地震反应谱的影响很大,在烈度相同的条件下,震中距越远,加速度谱曲线表现为( A )A.谱曲线峰值右移 B.谱曲线峰值左移C.谱曲线峰值增大 D.谱曲线峰值降低11、为保证结构“大震不倒”,要求结构具有( C )A.较大的初始刚度B.较高的截面承载能力C.较好的延性D.较小的自振周期T112、楼层屈服强度系数 沿高度分布比较均匀的结构,薄弱层的位置为(D )A.最顶层B.中间楼层C. 第二层D. 底层13、多层砖房抗侧力墙体的楼层水平地震剪力分配 ( B )A.与楼盖刚度无关B.与楼盖刚度有关C.仅与墙体刚度有关D.仅与墙体质量有关14、场地特征周期T g与下列何种因素有关?( C )A.地震烈度B.建筑物等级C.场地覆盖层厚度D.场地大小15、关于多层砌体房屋设置构造柱的作用,下列哪句话是错误的(D )A.可增强房屋整体性,避免开裂墙体倒塌B.可提高砌体抗变形能力C.可提高砌体的抗剪强度D.可抵抗由于地基不均匀沉降造成的破坏16、考虑内力塑性重分布,可对框架结构的梁端负弯矩进行调幅(B)A.梁端塑性调幅应对水平地震作用产生的负弯矩进行B.梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C.梁端塑性调幅应对内力组合后的负弯矩进行D.梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行17、水平地震作用标准值F ek的大小除了与质量,地震烈度,结构自振周期有关外,还与下列何种因素有关? ( B )A.场地平面尺寸B.场地特征周期C.荷载分项系数D.抗震等级18、表征地震动特性的要素有三个,下列哪项不属于地震动要素(B )A.加速度峰值B.地震烈度C.频谱特性D.地震持时19、震级大的远震与震级小的近震对某地区产生相同的宏观烈度,则对该地区产生的地震影响是(B )A.震级大的远震对刚性结构产生的震害大B.震级大的远震对柔性结构产生的震害大C.震级小的近震对柔性结构产生的震害大D.震级大的远震对柔性结构产生的震害小20、地震烈度主要根据下列哪些指标来评定( C )A.地震震源释放出的能量的大小B.地震时地面运动速度和加速度的大小C.地震时大多数房屋的震害程度、人的感觉以及其他现象D.地震时震级大小、震源深度、震中距、该地区的土质条件和地形地貌21、一般情况下,工程场地覆盖层的厚度应按地面至剪切波速大于多少的土层顶面的距离确定( D )A.200m/s B.300m/s C.400m/s D.500m/s22、关于地基土的液化,下列哪句话是错误的(A)A.饱和的砂土比饱和的粉土更不容易液化B.地震持续时间长,即使烈度低,也可能出现液化C.土的相对密度越大,越不容易液化D.地下水位越深,越不容易液化23、某地区设防烈度为7度,乙类建筑抗震设计应按下列要求进行设计(D )A.地震作用和抗震措施均按8度考虑B.地震作用和抗震措施均按7度考虑C.地震作用按8度确定,抗震措施按7度采用D.地震作用按7度确定,抗震措施按8度采用24、框架柱轴压比过高会使柱产生(B )A.大偏心受压构件B.小偏心受压构件C.剪切破坏D.扭转破坏25、钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定(B )A.抗震设防烈度、结构类型和房屋层数B.抗震设防烈度、结构类型和房屋高度C.抗震设防烈度、场地类型和房屋层数D.抗震设防烈度、场地类型和房屋高度26、纵波、横波和面波(L波)之间的波速关系为(A )A.V P > V S > V L B.V S > V P > V L C.V L > V P > V S D.V P > V L> V S27、位于软弱场地上,震害较重的建筑物是:(A )A.木楼盖等柔性建筑B.单层框架结构C.单层厂房结构D.多层剪力墙结构28、强剪弱弯是指:(B )A.抗剪承载力Vu大于抗弯承载力MuB.剪切破坏发生在弯曲破坏之后C.设计剪力大于设计弯矩D.柱剪切破坏发生在梁剪切破坏之后29、下列结构延性哪个延性在抗震设计时要求最高(D )A.结构总体延性B.结构楼层的延性C.构件的延性D.关键杆件的延性30、强柱弱梁是指:(B )A.柱线刚度大于梁线刚度B.柱抗弯承载力大于梁抗弯承载力C.柱抗剪承载力大于梁抗剪承载力 C.柱配筋大于梁配筋1、工程结构抗震设防的三个水准是什么?如何通过两阶段设计方法来实现?答:抗震设防的三个水准:第一水准:当遭受低于本地区抗震设防烈度的多遇地震影响时,一般不受损坏或不需修理仍可继续使用;第二水准:当遭受相当于本地区抗震设防烈度的地震影响时,可能损坏,经一般修理或不需修理仍可继续使用;第三水准:当遭受高于本地区抗震设防烈度的罕遇地震影响时,不致倒塌或发生危及生命的严重破坏。
普通多高层结构地震作用的计算方法

普通多高层结构地震作用的计算方法
一、底部剪力法。
这可是个挺常用的法子呢。
就想象这个建筑底部受到一个总的剪力,这个剪力就和地震作用有关啦。
它主要适用于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构。
计算的时候啊,先算出结构总的重力荷载代表值,然后根据一些经验系数之类的,就能得到底部剪力啦。
就像是给这个建筑底部来个“力量评估”,这个力量就是地震可能给它的冲击力。
这方法简单又直接,就像我们平时做事情找个最直接的办法一样。
二、振型分解反应谱法。
这个听起来有点复杂,其实也不难理解啦。
把建筑结构看成是好多振型的组合。
就好比一个人有好多不同的动作模式,建筑也有它不同的振动模式。
每个振型都有自己的频率、周期和振型参与系数。
通过计算每个振型下的地震作用,然后再把这些作用按照一定的规则组合起来,就得到了总的地震作用。
这就像是把建筑每个可能的振动“小情绪”都考虑进去,然后综合起来看它在地震时的反应。
这个方法能比较准确地反映结构在地震中的表现,不过计算起来相对底部剪力法要复杂那么一丢丢。
三、时程分析法。
这个方法就更酷啦。
它是直接输入地震波,然后看建筑结构在这个地震波的“刺激”下,随时间变化的反应。
就像是给建筑放一段地震的“小视频”,然后观察它的反应。
不过这个地震波的选择很重要哦,要根据建筑所在的场地类型、地震设防烈度等因素来选择合适的地震波。
这个方法可以详细地分析结构在地震过程中的各种情况,像结构的位移、内力等随时间的变化。
但是呢,它计算量超级大,就像做一个超级复杂的大工程一样。
工程结构抗震习题答案

掌握地震动的基本特性,结构地震响应特性,反应谱,钢筋混凝土结构、钢结构、砌体结构和桥梁结构的抗震验算和构造措施,隔震减震的基本原理等。
掌握排架结构简化为单质点体系时,多遇地震水平地震作用标准值的计算(例题3.1)钢筋混凝土框架简化成多质点体系时,用振型分解反应谱法计算该框架在多遇地震下的层间地震剪力,以及内力图。
(例题3.3)多层钢筋混凝土框架结构,用底部剪力法计算其在多遇地震作用下各质点上的水平地震作用。
(例题3.7)一、填空题1、构造地震为由于地壳构造运动造成地下岩层断裂或错动引起的地面振动。
2、建筑的场地类别,可根据土层等效剪切波速和场地覆盖层厚度划分为四类。
3、《抗震规范》将50年内超越概率为 10% 的烈度值称为基本地震烈度,超越概率为 63.2% 的烈度值称为多遇地震烈度。
4、丙类建筑房屋应根据抗震设防烈度,结构类型和房屋高度采用不同的抗震等级。
5、柱的轴压比n定义为 n=N/fc Ac(柱组合后的轴压力设计值与柱的全截面面积和混凝土抗压强度设计值乘积之比)6、震源在地表的投影位置称为震中,震源到地面的垂直距离称为震源深度。
7、表征地震动特性的要素有三,分别为振幅、频谱和持时。
8、某二层钢筋混凝土框架结构,集中于楼盖和屋盖处的重力荷载代表值相等G 1=G2=1200kN,第一振型φ12/φ11=1.618/1;第二振型φ22/φ21=-0.618/1。
则第一振型的振型参与系数j= 0、724 。
9、多层砌体房屋楼层地震剪力在同一层各墙体间的分配主要取决于楼盖的水平刚度(楼盖类型)和各墙体的侧移刚度及负荷面积。
10、建筑平面形状复杂将加重建筑物震害的原因为扭转效应、应力集中。
11、在多层砌体房屋计算简图中,当基础埋置较深且无地下室时,结构底层层高一般取至 室外地面以下500mm 处 。
12、某一场地土的覆盖层厚度为80米,场地土的等效剪切波速为200m/s,则该场地的场地土类别为 Ⅲ类场地 (中软土) 。
振型反应谱分析法和底部剪力法例题

334.2kN 334.4kN 167.4kN
− 120.8kN 120.7 kN 120.9kN
(4)计算各振型各楼层的水平 第一振型 地震作用 F j i = α j x j iγ j G i 第二振型 F 2 1 = 0 . 16 × ( − 0 . 428 ) × ( − 0 . 667 ) × 270 × 9 . 8 = 120 . 9 kN F 2 2 = 0 . 16 × ( − 0 . 428 ) × ( − 0 . 666 ) × 270 × 9 . 8 = 120 . 7 kN
例:试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8 类场地,设计地震分组为第二组。 抗震设防烈度为8度,Ⅱ类场地,设计地震分组为第二组。 解: 1)求体系的自振周期和振型 ( m = 180t
3
{X }1
0 .3 3 4 = 0 .6 6 7 1 .0 0 0
m2 = 270t
K 2 = 195MN/m
m1 = 270t K1 = 245MN/m
T1 = 0 . 46 7 s T 2 = 0 . 2 0 8 s T 3 = 0 . 1 3 4 s
(2)计算各振型的地震影响系数 α 1 = 0 . 1 3 9 α 2 = 0 . 16 α 3 = 0 . 1 6 (3)计算各振型的振型参与系数 γ 1 = 1 . 363 γ 2 = − 0 . 4 28 γ 3 = 0 . 06 3
3
{X }1
0 .3 3 4 = 0 .6 6 7 1 .0 0 0
{X }2
− 0 . 66 7 = − 0 . 666 1 . 00 0
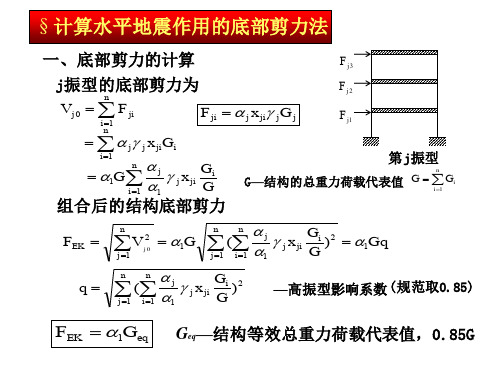
第三章-计算水平地震作用的底部剪力法4
K 2 195MN/m
m1 270t K1 245MN/m
解: (1 )计算结构等效总重力荷载代表值 Geq 5997.6kN (2 )计算水平地震影响系数 max 0.16 Tg 0.4s 1 0.139 (3 )计算结构总的水平地震作用标准值 FEK 833.7kN
0.30
Ⅱ 0.35
0.40
Ⅲ 0.45
0.55
Ⅳ 0.65
0.75
第三组
0.35
0.45
0.65
0.90
(3 )计算结构总的水 平地震作用标准值 FEK 1Geq
2 max
0.45 max
T ( g ) 2 max T
[2 0.2 1 (T 5Tg )] max
333.5 667.0 833.7
例 2 :六层砖混住宅楼,建造于基本烈度为8度 区,场地为Ⅱ类,设计地震分组为第一组,根 据各层楼板、墙的尺寸等得到恒荷和各楼面活 荷乘以组合值系数,得到的各层的重力荷载代 表值为 G 1=5399.7kN, G 2 =G 3=G4=G 5=5085kN, G 6 =3856.9kN 。试用底部剪力法计算各层在多遇 地震作用下剪力标准值。
k 1
FEk ---结构总水平地震作用标准值;
1 ---相应于结构基本周期的水平地震
影响系数;多层砌体房屋、底部框架 和多层内框架砖房,宜取水平地震影 响系数最大值;
Geq --- 结构等效总重力荷载; Fi --- i 质点水平地震作用; Gi ---i质点重力荷载代表值;
H i --- i 质点的计算高度;
多遇地震 罕遇地震
例 1 :试用底部剪力法计算图示框 架多遇地震时的层间剪力。已知 结构的基本周期T1=0.467s ,抗震 设防烈度为8度,Ⅱ类场地,设计地 震分组为第二组。
抗震习题

结构地震反应分析与抗震验算计算题3.1 单自由度体系,结构自振周期T=0.5S,质点重量G=200kN,位于设防烈度为8 度的Ⅱ类场地上,该地区的设计基本地震加速度为0.30g,设计地震分组为第一组,试计算结构在多遇地霞作用时的水平地震作用。
3.2 结构同题3.1,位于设防烈度为8度的Ⅳ类场地上,该地区的设计基本地震加速度为0.20g,设计地设分组为第二组,试计算结构在多遇地震作用时的水平地震作用。
3.3 钢筋混凝土框架结构如图所示,横梁刚度为无穷大,混凝土强度等级均为C25,一层柱截面450mm×450mm,二、三层柱截面均为 400mm×400mm,试用能量法计算结构的自振周期 T1。
3.4 题3.2的框架结构位于设防烈度为8度的Ⅱ类场地上,该地区的设计基本地震加速度为0.20g,设计地震分组为第二组,试用底部剪力法计算结构在多遇地震作用时的水平地震作用。
3.5 三层框架结构如图所示,横梁刚度为无穷大,位于设防烈度为8度的Ⅱ类场地上,该地区的设计基本地震加速为0.30g, 设计地震分组为第一组。
结构各层的层间侧移刚度分别为k1=7.5×105kN/m,k2=9.1×105kN/m,k3=8.5×105kN/m,各质点的质量分别为m1=2×106kg, m2=2×106kg, m3=1.5×105kg,结构的自震频率分别为ω1=9.62rad/s, ω2=26.88 rad/s, ω3=39.70 rad/s, 各振型分别为:要求:①用振型分解反应谱法计算结构在多遇地震作用时各层的层间地震剪力;②用底部剪力法计算结构在多遇地震作用时各层的层间地震剪力。
3.6 已知某两个质点的弹性体系(图3-6),其层间刚度为k1=k2=20800kN/m,,质点质量为m1=m2=50×103kg。
试求该体系的自振周期和振型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知:三层钢筋砼框架,各层质点重量及各阶阵型与相应周期如图所示。
8度、特征周期分组为一组、Ⅱ类场地。
求:计算多遇地震下各层住地震内力(分别用基底剪力法与振型分解法求解
)
(1)用振型分解反应普法计算
○
1主振型及相应的自振周期 由图可知,结构的主振型及相应的自振周期分别如下:
111213 1.0001.7482.049X X X ⎧⎫⎧⎫⎪⎪⎪⎪
=⎨⎬⎨⎬⎪⎪⎪⎪
⎩⎭⎩⎭ 212223 1.0000.0991.110X X X ⎧⎫⎧⎫
⎪⎪⎪⎪
=⎨⎬⎨⎬⎪⎪⎪⎪
-⎩⎭⎩⎭ 313233 1.0001.5301.489X X X ⎧⎫⎧⎫
⎪⎪⎪⎪=-⎨⎬⎨⎬⎪⎪⎪⎪
⎩
⎭⎩⎭ 10.788s T = 20.266s T = 30.178s
T = ○
2水平地震作用 相应于第一振型的质点水平地震作用为: 11111
11i i i i i
F X
G X m g αγαγ== 因10.35s<0.788s 5g Tg T T ==<,由图3.9、表3.2、表3.3得0.9γ=2 1.0η=max 0.16α=,可算得地震影响系数为:
0.9
12max 10.35 1.00.160.0770.788g T T γ
αηα⎛⎫⎛⎫
==⨯⨯= ⎪ ⎪
⎝⎭⎝⎭
可算得振型参与系数为:
1112
2
2
211
1166.211108.51.748594.52.049
0.6131166.21
1108.5
1.748594.5
2.049
n
i
i
i n
i i
i m X
m X
γ==⨯+⨯+⨯===⨯+⨯+⨯
∑∑
故 110.0770.6131116.621055.05F kN =⨯⨯⨯⨯= 120.0770.613 1.748110.851091.46F kN =⨯⨯⨯⨯= 130.0770.613 2.04959.451092.31F kN =⨯⨯⨯⨯= 相应于第二振型的质点水平地震作用为: 2222
i i i F X
m g αγ=
因20.1s<0.266s 0.35s T Tg =<=,故由图3.9可知: 22m a x
1.00.160.16
αηα==⨯= 又 ()()
21
22
2
2
221
1166.211108.50.099594.5 1.1100.3231166.211108.50.099594.5 1.110n
i
i
i n
i
i
i m X
m X
γ==⨯+⨯+⨯-==
=⨯+⨯+⨯-∑∑
故 210.160.3231116.621060.27F kN =⨯⨯⨯⨯= 220.160.3230.099110.8510 5.67F kN =⨯⨯⨯⨯= ()230.160.323 1.11059.451034.10F kN =⨯⨯-⨯⨯=- 相应于第三振型的质点水平地震作用为: 33
33
i i i F X m g αγ=
因20.1s<0.178s 0.35s T Tg =<=,故由图3.9可知:
22m a x
1.00.160.16
αηα==⨯= 又 ()()31
32
2
2
231
1166.211108.5 1.530594.5 1.4890.0701166.211108.5 1.530594.5 1.489
n
i
i
i n
i
i
i m X
m X
γ==⨯+⨯-+⨯==
=⨯+⨯-+⨯∑∑
故 310.160.0701116.621013.06F kN =⨯⨯⨯⨯= ()320.160.070 1.530110.851019.0F kN =⨯⨯-⨯⨯=- 320.160.070 1.48959.45109.91F kN =⨯⨯⨯⨯=
○
3层间地震剪力 根据以上计算,对应于第一、第二、第三振型的地震作用及剪力如图(a)、 (b)、 (c)所示。
按平方和开方法则,可求得底层、2层及3层的层间地震剪力如下:
1.97241
V k N =
=
2186.2V kN ==
398.9V kN =
=
框架的层间剪力图如图(d)所示。
振型分解反应谱法计算
(a )相应于第一振型的水平地震作用及剪力图;(b )相应于第二振型的水平地震作用及剪力图;(c )相应于第三振型的水平地震作用及剪力图;(d )框架层间剪力图
(2)用底部剪力法计算
○
1结构总水平地震作用 结构总水平地震作用为:
上式中的1α已经算出,其值为10.077α=;eq G 由计算其值为:
()1
0.850.85116.62+110.85+59.410=2438.82n
eq i i G m g kN ===⨯⨯∑
故 10.0772438.82187.79
E k e q
F G
k N α==⨯= ○
2各质点的地震作用 质点i 的水平地震作用为:
()1
1i i
i Ek n n
j
j
j G H F F G
H
δ==
-∑
因10.788 1.4 1.40.350.49g T s T s =>=⨯=,按表3.5
10.080.070.080.7880.070.1330n T δ=+=⨯+=
故
()
()()
()11
13
1
1116.6210 5.5
187.7910.133038.30116.6210 5.5110.8510 5.5+559.4510 5.5+5+5Ek n j
j
j G H F F G
H
kN
δ==
-⨯⨯=
⨯⨯-=⨯⨯+⨯⨯+⨯⨯∑
()
()
()()
()22
23
1
1110.8510 5.5+5 187.7910.133069.56116.6210 5.5110.8510 5.5+559.4510 5.5+5+5Ek n j
j
j G H F F G
H
kN
δ==
-⨯⨯=
⨯⨯-=⨯⨯+⨯⨯+⨯⨯∑
()
()
()()
()33
33
1
159.4510 5.555 187.7910.133055.07116.6210 5.5110.8510 5.5559.4510 5.555Ek n j
j
j G H F F G
H
kN
δ==
-⨯⨯++=
⨯⨯-=⨯⨯+⨯⨯++⨯⨯++∑顶部附加的集中水平地震作用为:
0.1330187.7924.n n E k F F k N
δ∆==⨯= 框架水平地震作用及层间剪力图如图所示。
底部剪力法计算的水平地震作用和剪力图。
