高考数学总复习教案:三角函数的综合应用
高三数学一轮复习教学案:三角函数
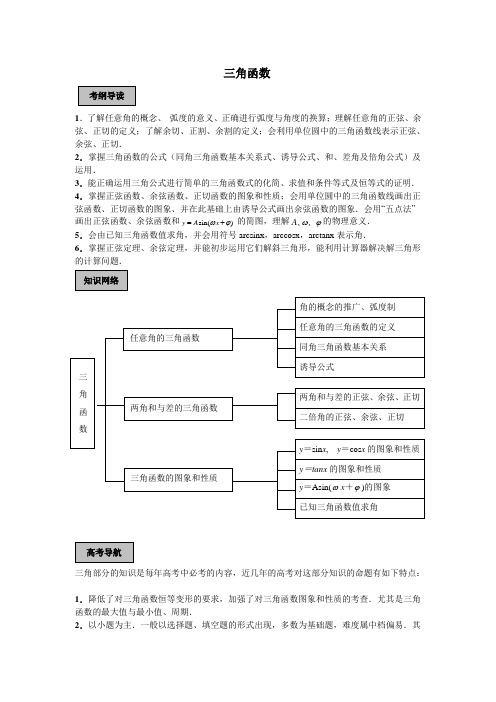
三角函数1.了解任意角的概念、弧度的意义、正确进行弧度与角度的换算;理解任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;会利用单位圆中的三角函数线表示正弦、余弦、正切.2.掌握三角函数的公式(同角三角函数基本关系式、诱导公式、和、差角及倍角公式)及运用.3.能正确运用三角公式进行简单的三角函数式的化简、求值和条件等式及恒等式的证明.4.掌握正弦函数、余弦函数、正切函数的图象和性质;会用单位圆中的三角函数线画出正弦函数、正切函数的图象、并在此基础上由诱导公式画出余弦函数的图象.会用“五点法”画出正弦函数、余弦函数和)(sin ϕω+=x A y 的简图,理解ϕω、A 、的物理意义.5.会由已知三角函数值求角,并会用符号arcsinx ,arccosx ,arctanx 表示角.6.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决解三角形的计算问题.三角部分的知识是每年高考中必考的内容,近几年的高考对这部分知识的命题有如下特点:1.降低了对三角函数恒等变形的要求,加强了对三角函数图象和性质的考查.尤其是三角函数的最大值与最小值、周期.2.以小题为主.一般以选择题、填空题的形式出现,多数为基础题,难度属中档偏易.其次在解答题中多数是三角函数式的恒等变形,如运用三角公式进行化简、求值解决简单的综合题等.3.更加强调三角函数的工具性,加强了三角函数与其它知识的综合,如在解三角形、立体几何、平面解析几何中考查三角函数的知识.第1课时 任意角的三角函数一、角的概念的推广1.与角α终边相同的角的集合为 .2.与角α终边互为反向延长线的角的集合为 .3.轴线角(终边在坐标轴上的角)终边在x 轴上的角的集合为 ,终边在y 轴上的角的集合为 ,终边在坐标轴上的角的集合为 .4.象限角是指: .5.区间角是指: .6.弧度制的意义:圆周上弧长等于半径长的弧所对的圆心角的大小为1弧度的角,它将任意角的集合与实数集合之间建立了一一对应关系.7.弧度与角度互化:180º= 弧度,1º= 弧度,1弧度= ≈ º.8.弧长公式:l = ;扇形面积公式:S = .二、任意角的三角函数9.定义:设P(x, y)是角α终边上任意一点,且 |PO| =r ,则sin α= ; cos α= ;tan α= ;10.三角函数的符号与角所在象限的关系:1213的正弦线、余弦线、正切线.- + -+cos x , + + --sin x ,- + +-tan x ,x y O xy O x y O2α,2α ,3α的终边所在位置.解: ∵α是第二象限的角,∴k·360°+90°<α<k·360°+180°(k ∈Z ).(1)∵2k·360°+180°<2α<2k·360°+360°(k ∈Z ),∴2α是第三或第四象限的角,或角的终边在y 轴的非正半轴上.(2)∵k·180°+45°<2α<k·180°+90°(k ∈Z ),当k=2n (n ∈Z )时,n·360°+45°<2α<n·360°+90°;当k=2n+1(n ∈Z )时,n·360°+225°<2α<n·360°+270°.∴2α是第一或第三象限的角.(3)∵k·120°+30°<3α<k·120°+60°(k ∈Z ),当k=3n (n ∈Z )时,n·360°+30°<3α<n·360°+60°;当k=3n+1(n ∈Z )时,n·360°+150°<3α<n·360°+180°;当k=3n+2(n ∈Z )时,n·360°+270°<3α<n·360°+300°.∴3α是第一或第二或第四象限的角.变式训练1:已知α是第三象限角,问3α是哪个象限的角?解: ∵α是第三象限角,∴180°+k·360°<α<270°+k·360°(k ∈Z ),60°+k·120°<3α<90°+k·120°.①当k=3m(m ∈Z )时,可得60°+m·360°<3α<90°+m·360°(m ∈Z ).故3α的终边在第一象限.②当k=3m+1 (m ∈Z )时,可得180°+m·360°<3α<210°+m·360°(m ∈Z ).故3α的终边在第三象限.③当k=3m+2 (m ∈Z )时,可得300°+m·360°<3α<330°+m·360°(m ∈Z ).故3α的终边在第四象限.综上可知,3α是第一、第三或第四象限的角. 例2. 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:(1)sin α≥23;(2)cos α≤21-.解:(1)作直线y=23交单位圆于A 、B 两点,连结OA 、OB ,则OA 与OB 围成的区域即为角α的终边的范围,故满足条件的角α的集合为α|2k π+3π≤α≤2k π+32π,k ∈Z .(2)作直线x=21-交单位圆于C 、D 两点,连结OC 、OD ,则OC 与OD 围成的区域(图中阴影部分)即为角α终边的范围.故满足条件的角α的集合为⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k k ,342322|ππαππα.变式训练2:求下列函数的定义域:(1)y=1cos 2-x ;(2)y=lg(3-4sin 2x ).解:(1)∵2cosx-1≥0,∴cosx≥21.由三角函数线画出x 满足条件的终边范围(如图阴影所示).∴x ∈⎥⎦⎤⎢⎣⎡+-32,32ππππk k (k ∈Z ).(2)∵3-4sin 2x >0,∴sin 2x <43,∴-23<sinx <23.利用三角函数线画出x 满足条件的终边范围(如右图阴影),∴x ∈(k π-3π,k π+3π)(k ∈Z ).例3. 已知角α的终边在直线3x+4y=0上,求sin α,cos α,tan α的值.解:∵角α的终边在直线3x+4y=0上,∴在角α的终边上任取一点P(4t,-3t) (t≠0),则x=4t,y=-3t,r=5)3()4(2222=-+=+t t y x |t|,当t >0时,r=5t, sin α=5353-=-=t t r y ,cos α=5454==t t r x , tan α=4343-=-=t t x y ; 当t <0时,r=-5t,sin α=5353=--=t t r y , cos α=5454-=-=t t rx , tan α=4343-=-=t t x y . 综上可知,t >0时,sin α=53-,cos α=54,tan α=43-; t <0时,sin α=53,cos α=-54,tan α=43-.变式训练3:已知角θ的终边经过点P ()(0),sin m m m θ≠=且,试判断角θ所在的象限,并求cos tan θθ和的值.解:由题意,得0,4r m m ==≠∴= 故角θ是第二或第三象限角.当m =,r =P 的坐标为(,cos tan x y r x θθ∴======当m =,r =P 的坐标为(,cos tan x y r x θθ∴======例4. 已知一扇形中心角为α,所在圆半径为R . (1) 若α3π=,R =2cm ,求扇形的弧长及该弧所在弓形面积;(2) 若扇形周长为一定值C(C>0),当α为何值时,该扇形面积最大,并求此最大值.解:(1)设弧长为l ,弓形面积为S 弓。
高三数学总复习 3.9三角函数的综合应用教案 新人教A版

2014届高三数学总复习 3.9三角函数的综合应用教案 新人教A版1. (必修5P 9例题4题改编)设△ABC 的三个内角A 、B 、C 所对的边分别是a 、b 、c ,且a cosA =c sinC,则A =________. 答案:π4解析:由a cosA =c sinC ,a sinA =c sinC ,得a sinA =a cosA ,即sinA =cosA ,所以A =π4.2. (必修4P 45习题1.3第8题改编)将函数y =sinx 的图象向左平移φ(0≤φ<2π)个单位后,得到函数y =sin ⎝⎛⎭⎪⎫x -π6的图象,则φ=________.答案:116π解析:将函数y =sinx 向左平移φ(0≤φ<2π)个单位得到函数y =sin(x +φ).只有φ=116π时有y =sin ⎝ ⎛⎭⎪⎫x +116π=sin ⎝⎛⎭⎪⎫x -π6.3. (必修4P 109习题3.3第6(2)题改编)tan π12-1tanπ12=________.答案:-2 3解析:原式=sin π12cos π12-cos π12sin π12=-⎝⎛⎭⎪⎫cos 2π12-sin 2π12sin π12cos π12=-cosπ612sin π6=-2 3. 4. (必修4P 115复习题第13题改编)已知函数f(x)=3sinxcosx -cos 2x +12(x∈R ),则f(x)在区间⎣⎢⎡⎦⎥⎤0,π4上的值域是________.答案:⎣⎢⎡⎦⎥⎤-12,32解析:f(x)=32sin2x -12cos2x =sin ⎝ ⎛⎭⎪⎫2x -π6.当x∈⎣⎢⎡⎦⎥⎤0,π4时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,π3,故值域为⎣⎢⎡⎦⎥⎤-12,32.5. 在△ABC 中,AC =7,BC =2,B =60°,则边BC 上的高为________. 答案:332解析:由余弦定理,得7=c 2+4-2c ,即c 2-2c -3=0,解得c =3,所以边BC 上的高h =3sin60°=332.1. 同角三角函数的基本关系式:sin 2α+cos 2α=1,tan α=sin αcos α.2. 两角和与差的正弦余弦和正切公式:sin(α±β)=sin αcos β±cos αsin β,cos(α±β)=cos αcos β sin αsin β,tan(α±β)=tan α±tan β1 tan αtan β.3. 二倍角公式:sin2α=2sin αcos α,cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α,tan2α=2tan α1-tan 2α. 4. 三角函数的图象和性质 5. 正弦定理和余弦定理:(1) 正弦定理:a sinA =b sinB =csinC=2R(R 为三角形外接圆的半径).(2) 余弦定理:a 2=b 2+c 2-2bccosA ,cosA =b 2+c 2-a22bc.题型1 三角恒等变换例1 已知sin ⎝ ⎛⎭⎪⎫A +π4=7210,A ∈⎝ ⎛⎭⎪⎫π4,π2.(1) 求cosA 的值;(2) 求函数f(x)=cos2x +52sinAsinx 的值域.解:(1) 因为π4<A<π2,且sin ⎝ ⎛⎭⎪⎫A +π4=7210,所以π2<A +π4<3π4,cos ⎝ ⎛⎭⎪⎫A +π4=-210.所以cosA =cos ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫A +π4-π4=cos ⎝ ⎛⎭⎪⎫A +π4cos π4+sin ⎝⎛⎭⎪⎫A +π4sin π4=-210²22+7210²22=35. (2) 由(1)可得sinA =45.所以f(x)=cos2x +52sinAsinx=1-2sin 2x +2sinx =-2⎝⎛⎭⎪⎫sinx -122+32,x ∈R .因为sinx ∈[-1,1],所以,当sinx =12时,f(x)取最大值32;当sinx =-1时,f(x)取最小值-3. 所以函数f(x)的值域为⎣⎢⎡⎦⎥⎤-3,32.备选变式(教师专享)(2013²上海卷)若cosxcosy +sinxsiny =12,sin2x +sin2y =23,则sin(x +y)=________.答案:23解析:由题意得cos(x -y)=12,sin2x +sin2y =sin[(x +y)+(x -y)]+sin[(x +y)-(x -y)]=2sin(x +y)cos(x -y)=23 sin(x +y)=23.题型2 三角函数的图象与性质例2 已知函数f(x)=Asin ⎝ ⎛⎭⎪⎫π3x +φ,x ∈R ,A>0,0<φ<π2,y =f(x)的部分图象如图所示,P 、Q 分别为该图象的最高点和最低点,点P 的坐标为(1,A).(1) 求f(x)的最小正周期及φ的值;(2) 若点R 的坐标为(1,0),∠PRQ =2π3,求A 的值.解:(1) 由题意得T =2ππ3=6.因为P(1,A)在y =Asin ⎝ ⎛⎭⎪⎫π3x +φ的图象上, 所以sin ⎝ ⎛⎭⎪⎫π3+φ=1.因为0<φ<π2,所以φ=π6.(2) 设点Q 的坐标为(x 0,-A). 由题意可知π3x 0+π6=3π2,得x 0=4,所以Q(4,-A).连结PQ ,在△PRQ 中,∠PRQ =2π3,由余弦定理得cos ∠PRQ =RP 2+RQ 2-PQ 22RP ²RQ =A 2+9+A 2-(9+4A 2)2A²9+A 2= -12,解得A 2=3.又A>0,所以A = 3. 备选变式(教师专享)已知函数f(x)=sin(ωx +φ)(ω>0,0≤φ≤π)为偶函数,且其图象上相邻两对称轴之间的距离为π.(1) 求函数f(x)的表达式;(2) 若sin α+f(α)=23,求2sin ⎝⎛⎭⎪⎫2α-π4+11+tan α的值.解:(1) ∵ f(x)为偶函数,∴ sin(-ωx +φ)=sin(ωx +φ),即2sin ωxcos φ=0恒成立, ∴ cos φ=0,又∵ 0≤φ≤π,∴ φ=π2. 又其图象上相邻对称轴之间的距离为π,∴ T =2π,∴ ω=1,∴f(x)=cosx.(2) ∵ 原式=sin2α-cos2α+11+tan α=2sin αcos α,又∵ sin α+cos α=23,∴ 1+2sinαcos α=49, 即2sin αcos α=-59,故原式=-59.题型3 正弦定理、余弦定理的综合应用例3 (2013²浙江)在锐角△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,且2asinB =3b.(1) 求角A 的大小;(2) 若a =6,b +c =8,求△ABC 的面积.解:(1) 由2asinB =3b 及正弦定理a sinA =b sinB ,得sinA =32.因为A 是锐角,所以A =π3.(2) 由余弦定理a 2=b 2+c 2-2bccosA ,得b 2+c 2-bc =36.又b +c =8,所以bc =283.由三角形面积公式S =12bcsinA ,得△ABC 的面积为733.备选变式(教师专享)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,C =π3,a =5,△ABC 的面积为10 3.(1) 求b ,c 的值;(2) 求cos ⎝⎛⎭⎪⎫B -π3的值.解:(1) 由已知,C =π3,a =5,因为S △ABC =12absinC ,即103=12b ²5sin π3,解得b =8.由余弦定理可得:c 2=25+64-80cos π3=49, 所以c =7.(2) 由(1)有cosB =25+49-6470=17,由于B 是三角形的内角,易知sinB =1-cos 2B =437,所以cos ⎝⎛⎭⎪⎫B -π3=cosBcos π3+sinBsin π3=17³12+437³32=1314.题型4 三角函数、平面向量、解三角形的综合应用例4 已知向量m =⎝ ⎛⎭⎪⎫sinA ,12与n =(3,sinA +3cosA)共线,其中A 是△ABC 的内角.(1) 求角A 的大小;(2) 若BC =2,求△ABC 面积S 的最大值,并判断S 取得最大值时△ABC 的形状. 解:(1) 因为m∥n ,所以sinA ²(sinA +3cosA)-32=0.所以1-cos2A 2+32sin2A -32=0,即32sin2A -12cos2A =1, 即sin ⎝ ⎛⎭⎪⎫2A -π6=1.因为A∈(0,π),所以2A -π6∈⎝ ⎛⎭⎪⎫-π6,11π6.故2A -π6=π2,A =π3.(2) 由余弦定理,得4=b 2+c 2-bc.又S △ABC =12bcsinA =34bc ,而b 2+c 2≥2bc bc +4≥2bc bc ≤4(当且仅当b =c 时等号成立), 所以S △ABC =12bcsinA =34bc≤34³4= 3.当△ABC 的面积取最大值时,b =c. 又A =π3,故此时△ABC 为等边三角形.备选变式(教师专享)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ,设向量m =(a ,b),n =(sin B ,sin A),p =(b -2,a -2).(1) 若m∥n ,求证:△ABC 为等腰三角形;(2) 若m⊥p ,边长c =2,角C =π3,求△ABC 的面积.(1) 证明:∵ m∥n ,∴ asin A =bsin B ,即a²a 2R =b²b2R ,其中R 是△ABC 外接圆半径,∴ a =b.∴ △ABC 为等腰三角形.(2) 解:由题意可知m²p =0,即a(b -2)+b(a -2)=0.∴ a+b =ab.由余弦定理可知,4=a 2+b 2-ab =(a +b)2-3ab ,即(ab)2-3ab -4=0,∴ab =4(舍去ab =-1),∴ S =12absin C =12³4³sin π3= 3.在已知值求角中,应合理选择三角函数形式进行求解,避免增根. 【示例】 (本题模拟高考评分标准,满分14分)若sin α=55,sin β=1010,且α、β均为锐角,求α+β的值. 学生错解: 解: ∵ α为锐角,∴ cos α=1-sin 2α=255.又β为锐角,∴ cos β=1-sin 2β=31010. ∵ sin(α+β)=sin αcos β+cos αsin β=22, 由于0°<α<90°,0°<β<90°, ∴ 0°<α+β<180°, 故α+β=45°或135°.审题引导: 在已知值求角中,角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能排除.要避免上述情况的发生,应合理选择三角函数形式进行求解,根据计算结果,估算出角的较精确的取值范围,并不断缩小角的范围,在选择三角函数公式时,一般已知正切函数值,选正切函数,已知正余弦函数值时,若角在(0,π)时,一般选余弦函数,若是⎝ ⎛⎭⎪⎫-π2,π2,则一般选正弦函数. 规范解答: 解: ∵ α为锐角,∴ cos α=1-sin 2α=255.(2分)又β为锐角,∴ cos β=1-sin 2β=31010.(4分) 且cos(α+β)=cos αcos β-sin αsin β=22,(10分) 由于0<α<π2,0<β<π2,所以0<α+β<π,因为y =cosx 在[]0,π上是单调递减函数,故α+β=π4.(14分)错因分析: 没有注意挖掘题目中的隐含条件,忽视了对角的范围的限制,造成出错. 事实上,仅由sin(α+β)=22,0°<α+β<180°而得到α+β=45°或135°是正确的,但题设中sin α=55<12,sin β=1010<12,使得0°<α<30°,0°<β<30°从而0°<α+β<60°,故上述结论是错误的.在已知值求角中,应合理选择三角函数形式进行求解,避免增根.本题中0<α+β<π,因为y =cosx 在[]0,π上是单调函数,所以本题先求cos(α+β)不易出错.1. (2013²常州期末)函数f(x)=cos πx 2cos π(x -1)2的最小正周期为________.答案:2解析:f(x)=cos πx 2cos π(x -1)2=cos πx 2²sin πx 2=12sin πx ,最小正周期为T =2ππ=2.2. (2013²北京期末)已知函数f(x)=sin ⎝ ⎛⎭⎪⎫x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π3,a ,若f(x)的值域是⎣⎢⎡⎦⎥⎤-12,1,则a 的取值范围是________.答案:⎣⎢⎡⎦⎥⎤π3,π解析:若-π3≤x ≤a ,则-π6≤x +π6≤a +π6,因为当x +π6=-π6或x +π6=7π6时,sin ⎝ ⎛⎭⎪⎫x +π6=12,所以要使f(x)的值域是⎣⎢⎡⎦⎥⎤-12,1,则有π2≤a +π6≤7π6,即π3≤a ≤π,即a 的取值范围是⎣⎢⎡⎦⎥⎤π3,π.3. (2013²北京期末)已知△ABC 中,AB =3,BC =1,sinC =3cosC ,则△ABC 的面积为________.答案:32解析:由sinC =3cosC ,得tanC =3>0,所以C =π3.根据正弦定理可得BC sinA =ABsinC ,即1sinA =332=2,所以sinA =12.因为AB>BC ,所以A<C ,所以A =π6,即B =π2,所以三角形为直角三角形,所以S △ABC =12³3³1=32.4. (2013²新课标Ⅰ卷)设当x =θ时,函数f(x)=sinx -2cosx 取得最大值,则cos θ=________.答案:-255解析:∵ f(x)=sinx -2cosx =5⎝ ⎛⎭⎪⎫55sinx -255cosx .令cos φ=55,sin φ=-255,则f(x)= 5(sinxcos φ+sin φcosx)=5sin(x +φ),当x +φ=2k π+π2,k ∈Z ,即x =2k π+π2-φ,k ∈Z 时,f(x)取最大值,此时θ=2k π+π2-φ,k ∈Z ,∴ cos θ=cos ⎝ ⎛⎭⎪⎫2k π+π2-φ=sin φ=-255.1. (2014²扬州期末)在锐角△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c.向量m =(1,cosB),n =(sinB ,-3),且m⊥n .(1) 求角B 的大小;(2) 若△ABC 面积为103,b =7,求此三角形周长.解:(1) m²n =sinB -3cosB ,∵ m ⊥n ,∴ m ²n =0, ∴ sinB -3cosB =0.∵ △ABC 为锐角三角形,∴ cosB ≠0,∴ tanB = 3.∵ 0<B<π2,∴ B =π3.(2) ∵ S △ABC =12acsinB =34ac ,由题设34ac =103,得ac =40.由72=a 2+c 2-2accosB ,得49=a 2+c 2-ac ,∴ (a +c)2=(a 2+c 2-ac)+3ac =49+120=169.∴ a+c =13,∴ 三角形周长是20. 2. 在△ABC 中, a 、b 、c 分别是角A 、B 、C 的对边,△ABC 的周长为2+2,且sinA +sinB =2sinC.(1) 求边c 的长;(2) 若△ABC 的面积为13sinC ,求角C 的度数.解:(1) 在△ABC 中, ∵ sinA +sinB =2sinC ,由正弦定理,得a +b =2c ,∴ a +b +c =2c +c =(2+1)c =2+2.∴ a +b =2,c = 2.(2) 在△ABC 中, S △ABC =12absinC =13sinC ,∴ 12ab =13 ,即ab =23. 又a +b =2,在△ABC 中,由余弦定理,得cosC =a 2+b 2-c 22ab =(a +b )2-2ab -22ab =12,又在△ABC 中∠C∈(0,π),∴ ∠C =60°. 3. (2013²湖北卷)在△ABC 中,角A 、B 、C 对应的边分别是a 、b 、c.已知cos2A -3cos(B +C)=1.(1) 求角A 的大小;(2) 若△ABC 的面积S =53,b =5,求sinBsinC 的值.解:(1) 由已知条件得:cos2A +3cosA =1,∴ 2cos 2A +3cosA -2=0,解得cosA =12,∴ ∠A =60°.(2) S =12bcsinA =53 c =4,由余弦定理,得a 2=21,(2R)2=a 2sin 2A =28,∴ sinBsinC=bc 4R 2=57. 4. (2013²北京卷)在△ABC 中,a =3,b =26,∠B =2∠A. (1) 求cosA 的值; (2) 求c 的值.解:(1) 因为a =3,b =26,∠B =2∠A.所以在△ABC 中,由正弦定理得3sinA =26sin2A .所以2sinAcosA sinA =263.故cosA =63.(2) 由(1)知cosA =63,所以sinA =1-cos 2A =33. 又因为∠B=2∠A,所以cosB =2cos 2A -1=13.所以sinB =1-cos 2B =223.在△ABC 中,sinC =sin(A +B)=sinAcosB +cosAsinB =539.所以c =sin sin a CA=5.1. 三角变换的基本策略是化异为同,即将函数名称、角、次数等化异为同.2. 对于函数y =Asin(ωx +φ)+B ,常用“五点法”画图象,运用整体思想研究性质.3. 求三角函数的单调区间、周期,及判断函数的奇偶性,要注意化归思想的运用,通过恒等变换转化为基本三角函数类型,注意变形前后的等价性.4. 解三角函数的综合题时应注意:(1) 与已知基本函数对应求解,即将ωx +φ视为一个整体X ;(2) 将已知三角函数化为同一个角的一种三角函数,如y =Asin(ωx +φ)+B 或y =asin2x +bsinx +c ;(3) 换元方法在解题中的运用.请使用课时训练(B)第9课时(见活页).[备课札记]。
三角函数的综合应用+课件-2025届高三数学一轮复习

(2)由题意,得 f(A)=2sin 2A-π3- 3=0,即 sin 2A-π3= 23,
∵A∈0,π2, 则 2A-π3∈-π3,23π, ∴2A-π3=π3,∴A=π3.
在△ABC 中, 由 a2=b2+c2-2bc cos A=42+32-2×4×3×12=13, 可得 a= 13, 又∵12bc sin A=12AD×a,即12×4×3× 23=21AD× 13, ∴AD=61339,故 BC 边上的高 AD 的长为61339.
(2)根据正弦定理得sina A=sinc C=sinb
B=
4 =8 3
3
3,
2
所以
a=8
3
3 sin
A,c=8
3
3 sin
C.
所以
a+c=8
3
3 (sin
A+sin
C).
因为 A+B+C=π,B=π3,所以 A+C=23π,
所以 a+c=8
3
3 sin
A+sin
23π-A=8
3
33 2sin
A+
23cos
A
=8sin A+π6.
因为 0<A<23π,
所以 A+π6∈π6,56π,所以 sin A+π6∈12,1,则 a+c∈(4,8].
所以 a+c 的取值范围是(4,8].
【反思感悟】已知三角形一边及其对角,求取值范围的问题 的解法
(1)(不妨设已知 a 与 sin A 的值)根据 2R=sina A求出三角形外接
∴a2+c2 b2=sin2Asi+n2Csin2B=cos22sCin+2Ccos2C =(1-2sin2Cs)in2+2C(1-sin2C)=2+4sins4iCn2-C 5sin2C
高考数学专题讲座 第7讲 三角函数的综合应用

高考数学专题讲座 第7讲 三角函数的综合应用一、考纲要求1.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式; 2.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明; 3.会由已知三角函数值求角,并会用符号arcsin x, arcos x,arctan x 表示角;4.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决解三角形的计算问题.二、基础过关 1.设α、β是一个钝角三角形的两个锐角, 下列四个不等式中不正确的是( ).A .tan αtan β<1B .sin α+sin β<2C .cos α+cos β>1D .21tan(α+β)<tan 2βα+ 2.在△ABC 中,∠A=60°,b =1,△ABC 面积为3,则CB B cb a sin sin sin ++++的值为( ).A .8138 B .3932C .3326D .72 3.)sin()(ϕω+=x A x f (A >0,ω>0)在x =1处取最大值,则( ). A .)1(-x f 一定是奇函数 B .)1(-x f 一定是偶函数C .)1(+x f 一定是奇函数D .)1(+x f 一定是偶函数4.已知方程x 2+4ax +3a +1=0(a >1)的两根均tan α、tan β,且α,β∈(-2,2ππ),则tan 2βα+的值是( ).A .21 B .2- C .34 D .21或2- 5.给出四个命题:(1)若sin2A =sin2B ,则△ABC 为等腰三角形; (2)若sin A =cos B ,则△ABC 为直角三角形;(3)若sin 2A +sin 2B +sin 2C <2,则△ABC 为钝角三角形;(4)若cos(A -B )cos(B -C )cos(C -A )=1,则△ABC 为正三角形. 以上正确命题的个数是( ).A .1B .2C .3D .46.x x x f 32cos 32sin )(+=的图象中相邻的两条对称轴间距离为( ).A .3πB .π34C .π23D .π677.︒+︒+︒+︒10cos 1)370tan 31(100sin 130sin 2= .8.下列命题正确的有 . (1)若-2π<α<β<2π,则βα-范围为(-π,π);(2)若α在第一象限,则2α在第一、三象限; (3)若θsin =53+-m m ,524cos +-=m mθ,则m ∈(3,9);(4)2sin θ=53,2cos θ=54-,则θ在第三、四象限.三、典型例题例1 已知:定义在]4,(-∞上的减函数)(x f ,使得)cos 4721()sin (2x m f x m f +-+≤- 对一切实数x 均成立,求实数m 的范围.例2 化工厂的主控制表盘高1米,表盘底边距地面2米,问值班人员坐在什么位置上表盘看得最清楚?(设值班人员坐在椅子上时,眼睛距地面2.1米)例3 已知向量a →=(2,2),向量b →与向量a →的夹角为43π,且a →·b →=-2.(1)求向量b →;(2)若t →=(1,0),且b →⊥t →,c →=(cosA,22cos 2C ),其中A ,C 是△ABC 的内角,若三角形的三内角A 、B 、C 依次成等差数列,试求|b →+c →|的取值范围.四、 热身演练 1.已知,那么下列命题成立的是( ).A .若α,β是第一象限角,则βαcos cos >B .若α,β是第二象限角,则βαtan tan >C .若α,β是第三象限角,则βαcos cos >D .若α,β是第四象限角,则βαtan tan > 2.函数的部分图象是( ).3.函数的反函数是( ).A .)20)(1arccos(≤≤--=x x yB .)20)(1arccos(≤≤--=x x y πC .)20)(1arccos(≤≤-=x x yD .)20)(1arccos(≤≤-+=x x y π4.任意实数x,不等式 ),,(0cos sin R c b a c x b x a ∈>++都成立的充要条件是( ).A .00>==c b a 且B .c b a =+22C .c b a <+22D .c b a >+225.若1cos sin =+θθ,则对任意的实数n ,θθnncos sin +的取值范围是( ).A .1B .(0,1)C .121-n D .无法确定6.定义在R 上的偶函数f (x )满足f (x+2)=f (x ),且f (x )在[-3,-2]上是减函数,又α,β是锐角三角形的两内角,则( ).A .)(cos )(sin βαf f >B .)(cos )(sin βαf f <C .)(sin )(sin βαf f >D .)(cos )(cos βαf f <7.下列说法正确的是(填上你认为正确的所有命题的代号) . ①函数y=-sin(kπ+x)(k∈Z)是奇函数; ②函数y=2sin(2x+π/3)关于点(π/12,0)对称;③函数y =sin(2x+π/3)+sin(2x -π/3)的最小正周期是π;④ΔABC 中cosA>cosB 的充要条件是A<B ; 8.在△ABC 中,sinA+cosA=137,则AA A A cos 7sin 15cos 4sin 5-+= .9.如右图,在半径为R 的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r 的平方成反比,即I =k ·2sin r θ,其中 k 是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h ,才能使桌子边缘处最亮?10.设关于x 的方程sinx+3cosx+a=0在(0, 2π)内有相异二解α、β. (1)求α的取值范围; (2)求tan(α+β)的值.12.设α、β、γ是锐角,且tan 2α=2tan 3γ,tan β=21tan γ求证:α、β、γ成等差数列.三角函数的综合应用一、考纲要求:1. 掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式 2. 能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明. 3. 会由已知三角函数值求角,并会用符号arcsin x, arcos x,arctan x 表示角.4.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决解三角形的计算问题. 二、基础过关: 1.设α、β是一个钝角三角形的两个锐角, 下列四个不等式中不正确的是( A ).A .tan αtan β<1B .sin α+sin β<2C .cos α+cos β>1D .21tan(α+β)<tan 2βα+ 2.在△ABC 中,∠A=60°,b =1,△ABC 面积为3,则CB B cb a sin sin sin ++++的值为( B ).A .8138 B .3932C .3326D .72 3.)sin()(ϕω+=x A x f (A >0,ω>0)在x =1处取最大值,则( D ). A .)1(-x f 一定是奇函数 B .)1(-x f 一定是偶函数C .)1(+x f 一定是奇函数D .)1(+x f 一定是偶函数4.已知方程x 2+4ax +3a +1=0(a >1)的两根均tan α、tan β,且α,β∈(-2,2ππ),则tan2βα+的值是( B ).A .21B .2-C .34D .21或2- 5.给出四个命题:(1)若sin2A =sin2B ,则△ABC 为等腰三角形;(2)若sin A =cos B ,则△ABC 为直角三角形;(3)若sin 2A +sin 2B +sin 2C <2,则△ABC 为钝角三角形;(4)若cos(A -B )cos(B -C )cos(C -A )=1,则△ABC 为正三角形.以上正确命题的个数是( B ).A .1B .2C .3D .46.x x x f 32cos 32sin )(+=的图象中相邻的两条对称轴间距离为( C ).A .3πB .π34C .π23D .π677.︒+︒+︒+︒10cos 1)370tan 31(100sin 130sin 2= .28.下列命题正确的有 .(2)(1)若-2π<α<β<2π,则βα-范围为(-π,π); (2)若α在第一象限,则2α在第一、三象限;(3)若θsin =53+-m m ,524cos +-=m mθ,则m ∈(3,9);βφαDCBA1.2 m2 m 1 m (4)2sinθ=53,2cosθ=54-,则θ在第三、四象限. 三、典型例题例1 已知:定义在]4,(-∞上的减函数)(x f ,使得)cos 4721()sin (2x m f x m f +-+≤- 对一切实数x 均成立,求实数m 的范围.解:由题意可得 ⎪⎩⎪⎨⎧≤-+-+≥-4sin cos 4721sin 2x m xm x m , 即 ⎪⎩⎪⎨⎧+≤-+-≥+-xm x x m m sin 443sin sin 212恒成立对R x ∈,又 21)21(sin 43sin 2sin 2---=-+-x x x ,∴3sin 4≥+x ,∴⎪⎩⎪⎨⎧≤-≥+-32121m m m , ∴⎪⎩⎪⎨⎧≤+≥+32121m m m , ∴21-=m ,或323≤<m例2 化工厂的主控制表盘高1米,表盘底边距地面2米,问值班人员坐在什么位置上表盘看得最清楚?(设值班人员坐在椅子上时,眼睛距地面2.1米)解:如图,8.02.12=-=CD ,设x AD =,则x x AD BD 8.18.01tan =+==α, xAD CD 8.1tan ==β, βαβαβαφtan tan 1tan tan )tan(tan +-=-= ,∴4.2144.12144.118.08.118.08.1tan =⋅≤+=⋅+-=xx x x x x x x φ当xx 44.1=,即2.1=x 时, φtan 达到最大值4.21,φ是锐角,φtan 最大时,φ也最大,所以值班人员看表盘最清楚的位置为2.1=AD 米.例3 已知向量a →=(2,2),向量b →与向量a →的夹角为43π,且a →·b →=-2,(1)求向量b →;(2)若t →=(1,0),且b →⊥t →,c →=(cosA,22cos 2C ),其中A ,C 是△ABC 的内角,若三角形的三内角A 、B 、C 依次成等差数列,试求|b →+c →|的取值范围.解:(1)设b →=(x,y ),则2x+2y=-2,且a →·b →=|b →||c →|cos 43π=22y x +×22×(-22)=-2,解得⎩⎨⎧=-=01y x 或⎩⎨⎧-==1y x , ∴b →=(-1,0) 或b →=(0,-1).(2)∵三角形的三内角A 、B 、C 依次成等差数列,∴b=3π,∵b →⊥t →,∴b →=(0,-1),∴b →+c →=( cosA,22cos 2C -1)=(cosA,cosC),∴|b →+c →|2=C A 22cos cos +=1+21(cos2A+cos2C)=1+cos(A+C)cos(A -C)=1-21cos(A -C),∴-32π<A -C<32π ,∴-21<cos(A -C)≤1,22≤|b →+c →|<25.例4 已知△ABC 的三内角A 、B 、C 满足A +C =2B ,设x =cos2CA -, f (x )=cosB (CA cos 1cos 1+). (1)试求函数f (x )的解析式及其定义域; (2)判断其单调性,并加以证明; (3)求这个函数的值域. 解:(1)∵A +C =2B ,∴B =60°,A +C =120°)cos()cos(2cos2cos2cos cos cos cos 21)(C A C A CA C A C A C A x f -++-+=⋅+⋅= 342122122-=-+-=x xx x , ∵0°≤|2C A -|<60°,∴x =cos 2C A -∈(21,1].又4x 2-3≠0,∴x ≠23,∴定义域为(21,23)∪(23,1). (2)设x 1<x 2,∴f (x 2)-f (x 1)=342342211222---x x x x=)34)(34()34)((222212121--+-x x x x x x ,若x 1,x 2∈(23,21),则4x 12-3<0,4x 22-3<0,4x 1x 2+3>0,x 1-x 2<0,∴f (x 2)-f (x 1)<0,即f (x 2)<f (x 1),若x 1,x 2∈(23,1],则4x 12-3>0. 4x 22-3>0,4x 1x 2+3>0,x 1-x 2<0,∴f (x 2)-f (x 1)<0.即f (x 2)<f (x 1),∴f (x )在(21,23)和(23,1]上都是减函数.(3)由(2)知,f (x )<f (21)=-21或f (x )≥f (1)=2.故f (x )的值域为(-∞,-21)∪[2,+∞). 四、热身演练: 1.已知,那么下列命题成立的是( B ).A .若α,β是第一象限角,则βαcos cos >B .若α,β是第二象限角,则βαtan tan >C .若α,β是第三象限角,则βαcos cos >D .若α,β是第四象限角,则βαtan tan > 2.函数的部分图象是( D ).AB C D3.函数的反函数是( A ).A .)20)(1arccos(≤≤--=x x yB .)20)(1arccos(≤≤--=x x y πC .)20)(1arccos(≤≤-=x x yD .)20)(1arccos(≤≤-+=x x y π4.任意实数x,不等式 ),,(0cos sin R c b a c x b x a ∈>++都成立的充要条件是( C ).A .00>==c b a 且B .c b a =+22C .c b a <+22D .c b a >+225.若1cos sin =+θθ,则对任意的实数n ,θθnncos sin +的取值范围是( D ).A .1B .(0,1)C .121-n D .无法确定6.定义在R 上的偶函数f (x )满足f (x+2)=f (x ),且f (x )在[-3,-2]上是减函数,又α,β是锐角三角形的两内角,则( A ).A .)(cos )(sin βαf f >B .)(cos )(sin βαf f <C .)(sin )(sin βαf f >D .)(cos )(cos βαf f <7.下列说法正确的是(填上你认为正确的所有命题的代号) .①②③④ ①函数y=-sin(k π+x)(k ∈Z)是奇函数; ②函数y=2sin(2x+π/3)关于点 (π/12,0)对称;③函数y=sin(2x+π/3)+sin(2x-π/3)的最小正周期是π; ④ΔABC 中cosA>cosB 的充要条件是A<B ; 8.在△ABC 中,sinA+cosA=137,则AA A A cos 7sin 15cos 4sin 5-+= .4389.如右图,在半径为R 的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r 的平方成反比,即I =k ·2sin r θ,其中 k 是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h ,才能使桌子边缘处最亮?解:R =r cos θ,由此得:20,cos 1π<θ<θ=R r , RR h R k I Rk R k I R k R k r k I 22tan ,33sin ,392)32()()sin 1)(sin 1(sin 2)(2)cos (sin cos sin sin 232222222222222=θ==θ⋅≤⋅≤θ-θ-⋅θ⋅=θ⋅θ⋅=θ⋅θ⋅=θ⋅=此时时成立等号在由此得 10.设关于x 的方程sinx+3cosx+a=0在(0, 2π)内有相异二解α、β. (1)求α的取值范围; (2)求tan(α+β)的值. 解:(1)∵sinx+3cosx=2(21sinx+23cosx)=2 sin(x+3π),∴方程化为sin(x+3π)=-2a .∵方程sinx+3cosx+a=0在(0, 2π)内有相异二解,∴sin(x+3π)≠sin 3π=23. 又sin(x+3π)≠±1 (∵当等于23和±1时仅有一解),∴|-2a |<1,且-2a≠23, 即|a|<2,且a ≠-3.,∴a 的取值范围是(-2, -3)∪(-3, 2).(2) ∵α、 β是方程的相异解,∴sin α+3cos α+a=0 ① sin β+3cos β+a=0 ②①-②得(sin α- sin β)+3( cos α- cos β)=0, ∴ 2sin 2βα-cos2βα+-23sin 2βα+,sin2βα-=0,又sin2βα+≠0,∴tan2βα+=33, ∴tan(α+β)=2tan 22tan22βαβα+-+=3.11.求20sin 6420cos 120sin 3222+-的值.解:原式=20cos 20sin 20sin 20cos 32222-+64sin 220°=40sin 41)20sin 20cos 3)(20sin 20cos 3(2+-+64sin 220°=40sin 41)2030cos()2030cos(42-++64sin 220°=40sin 80sin 40sin 162+64sin 220°=32cos40°+64(240cos 1-)=32.12.设α、β、γ是锐角,且tan 2α=2tan 3γ,tan β=21tan γ求证:α、β、γ成等差数列.解:要证α、β、γ成等差数列,∵α、β、γ是锐角,只要证:tan β=tan 2γα+.∵tan 2γα+=2tan2tan12tan2tanγαγα-+=2tan2tan12tan 2tan 33γγγγ-+=)2tan 1)(2tan 1()2tan 1(2tan222γγγγ+-+=212tan 12tan22γγ-=21tan γ= tan β.∴α、β、γ成等差数列.。
2015高考总复习数学(文)课件:6.6三角函数的综合应用

2.三角公式的三大作用 (1)三角函数式的化简. (2)三角函数式的求值. (3)三角函数式的证明. 3.求三角函数最值的常用方法
(1)配方法.(2)化为一个角的三角函数.
(3)数形结合法.(4)换元法.(5)基本不等式法等.
1.函数 y=cos2x+2sinxcosx 的最小正周期 T=( B )
【互动探究】 3.已知函数 f(x)=(sin2x+cos2x)2-2sin22x. (1)求 f(x)的最小正周期;
π (2)若函数 y=g(x)的图象是由 y=f(x)的图象向右平移8个单 位长度,再向上平移 1 个单位长度得到的,当
π x∈0,4时,求
y=g(x)的最大值和最小值.
2.
3π π 5 π 5π 由 0≤x≤ 5 ,得-6≤3x-6≤ 6 , 5 π 1 所以-2≤sin3x-6≤1, 5 π 得-1- 2≤2sin3x-6- 2≤2- 2. 3π 故函数 f(x)在0, 5 上的取值范围为[-1- 2,2- 2].
解:(1)因为 f(x)=(sin2x+cos2x)2-2sin22x
=sin4x+cos4x=
π 2sin4x+4,
2π π 所以函数的最小正周期为 T= 4 =2.
(2)依题意有 y=g(x)= =
π 2sin4x-4+1.
π π 2sin4x-8+4+1
一问结合图形求得周期
11π 5π T=2 12 -12=π,从而求得
2π ω= T =2.
再利用特殊点在图象上求出 ,A,从而求出 f(x)的解析式;第 二问运用第一问结论和三角恒等变换及 y=Asin(ωx+ )的单调 性求得.
【互动探究】
高三数学总复习 专题二三角函数教学案

芯衣州星海市涌泉学校赣榆县智贤中学高三数学总复习专题二第1讲三角函数〔1〕教学案教学内容:三角函数的图象与性质〔1〕教学目的:1三角函数的图象与解析式2.利用三角函数的图象与解析式教学重点:1.求三角函数的解析式;教学难点:三角函数的图象与解析式教学过程:一、知识点复习:1.必记的概念与定理(1)同角关系:sin2α+cos2α=1,=tanα.(2)诱导公式:在+α,k∈Z的诱导公式中“奇变偶不变,符号看象限〞.(3)三角函数的图象及常用性质函数y=sinx y=cosx y=tanx图象单调性在[-+2kπ,+2kπ](k∈Z)上单调递增;在[+2kπ,+2kπ](k∈Z)上单调递减在[-π+2kπ,2kπ](k∈Z)上单调递增;在[2kπ,π+2kπ](k∈Z)上单调递减在(-+kπ,+kπ)(k∈Z)上单调递增对称性对称中心:(kπ,0)(k∈Z);对称轴:x=+kπ(k∈Z)对称中心:(+kπ,0)(k∈Z);对称轴:x=kπ(k∈Z)对称中心:(,0)(k∈Z)2.记住几个常用的公式与结论对于函数y=Asin(ωx+φ)(A>0,ω>0)要记住下面几个常用结论:(1)定义域:R.(2)值域:[-A,A].当x=(k∈Z)时,y取最大值A;当x=(k∈Z)时,y取最小值-A.(3)周期性:周期函数,周期为.(4)单调性:单调递增区间是(k∈Z);单调递减区间是(k∈Z).(5)对称性:函数图象与x轴的交点是对称中心,即对称中心是(,0),对称轴与函数图象的交点纵坐标是函数的最值,即对称轴是直线x=,其中k∈Z.(6)函数y=Asin(ωx+φ)(A>0,ω>0)中,A影响函数图象的最高点和最低点,即函数的最值;ω影响函数图象每隔多少重复出现,即函数的周期;φ影响函数的初相.(7)对于函数y=Asin(ωx+φ)(A>0,ω>0)的图象,相邻的两个对称中心或者者两条对称轴相距半个周期;相邻的一个对称中心和一条对称轴相距周期的四分之一.复备栏3.需要关注的易错易混点三角函数图象平移问题(1)看平移要求:拿到这类问题,首先要看题目要求由哪个函数平移到哪个函数,这是判断挪动方向的关键点.(2)看挪动方向:在学习中,挪动的方向一般我们会记为“正向左,负向右〞,其实,这样不理解的记忆是很危险的.上述规那么不是简单地看y=Asin(ωx+φ)中φ的正负,而是和它的平移要求有关.正确地理解应该是:平移变换中,将x变换为x+φ,这时才是“正向左,负向右〞.(3)看挪动单位:在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系,φ是初相位,再经过ω的压缩,最后挪动的单位是||.二、根底训练:1.函数y=tan的定义域是________.解析:∵x-≠kπ+,∴x≠kπ+,k∈Z.答案:2.(2021·模拟)函数f(x)=sinxcosx的最小正周期是________.解析:由题知f(x)=sin2x,所以T==π.答案:π3.将函数y=2sinx的图象上每一点向右平移1个单位长度,再将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变),得函数y=f(x)的图象,那么f(x)的解析式为________.解析:函数y=2sinx向右平移1个单位得y=2sin(x-1)=2sin,将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变),那么y=2sin,即y=2sin.答案:y=2sin4.(2021·模拟)函数f(x)=2sin,x∈[-π,0]的单调增区间为________.解析:当x-∈,k∈Z时,f(x)单调递增,又因为x∈[-π,0],故取k=0得x∈.答案:1三、例题教学:例1、(2021·模拟)假设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如下列图,这个函数的解析式为________.[解析]由题意知:周期T=2(-)=π,ω==2,设f(x)=Asin(2x+φ),点(,0)为五点作图中的第三点,所以2×+φ=π,即φ=.设f(x)=Asin(2x+),因为点(0,)在原函数的图象上,故Asin=,所以A=,综上知:f(x)=sin(2x+).[答案]f(x)=sin(2x+)变式训练:1.(2021·高考卷)函数y=cosx与y=sin(2x+φ)(0≤φ<π),它们的图象有一个横坐标为的交点,那么φ的值是________.解析:由题意,得sin=cos,因为0≤φ<π,所以φ=.答案:例2、2021·模拟)函数f(x)=2sin(ωx+φ)(ω>0,-<φ<)的图象如下列图,直线x=,x =是其两条对称轴.(1)求函数f(x)的解析式并写出函数的单调增区间;(2)假设f(α)=,且<α<,求f(+α)的值.[解](1)由题意,=-=,∴T=π,又ω>0,故ω=2,∴f(x)=2sin(2x+φ),由f()=2sin(+φ)=2,解得φ=2kπ-(k∈Z),又-<φ<,∴φ=-,∴f(x)=2sin(2x-),由2kπ-≤2x-≤2kπ+(k∈Z)知,kπ-≤x≤kπ+,(k∈Z),∴函数f(x)的单调增区间为[kπ-,kπ+](k∈Z).(2)依题意得:2sin(2α-)=,即sin(2α-)=,∵<α<,∴0<2α-<,∴cos(2α-)===,f(+α)=2sin[(2α-)+],∵sin[(2α-)+]=sin(2α-)cos+cos(2α-)sin=(+)=,∴f(+α)=.稳固练习:完成专题强化训练。
高考数学第二轮专题复习三角函数教案
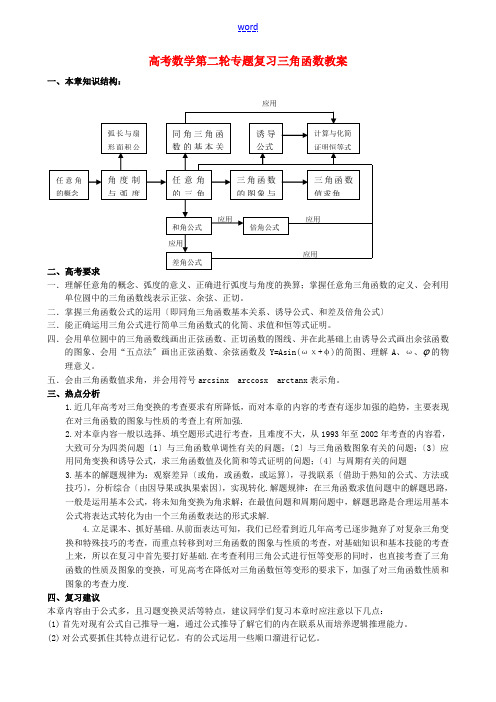
高考数学第二轮专题复习三角函数教案一、本章知识结构:应用一.理解任意角的概念、弧度的意义、正确进行弧度与角度的换算;掌握任意角三角函数的定义、会利用单位圆中的三角函数线表示正弦、余弦、正切。
二.掌握三角函数公式的运用〔即同角三角函数基本关系、诱导公式、和差及倍角公式〕三.能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明。
四.会用单位圆中的三角函数线画出正弦函数、正切函数的图线、并在此基础上由诱导公式画出余弦函数的图象、会用“五点法〞画出正弦函数、余弦函数及Y=Asin(ωχ+φ)的简图、理解A、ω、 的物理意义。
五.会由三角函数值求角,并会用符号arcsinx arccosx arctanx表示角。
三、热点分析1.近几年高考对三角变换的考查要求有所降低,而对本章的内容的考查有逐步加强的趋势,主要表现在对三角函数的图象与性质的考查上有所加强.2.对本章内容一般以选择、填空题形式进行考查,且难度不大,从1993年至2002年考查的内容看,大致可分为四类问题〔1〕与三角函数单调性有关的问题;〔2〕与三角函数图象有关的问题;〔3〕应用同角变换和诱导公式,求三角函数值及化简和等式证明的问题;〔4〕与周期有关的问题3.基本的解题规律为:观察差异〔或角,或函数,或运算〕,寻找联系〔借助于熟知的公式、方法或技巧〕,分析综合〔由因导果或执果索因〕,实现转化.解题规律:在三角函数求值问题中的解题思路,一般是运用基本公式,将未知角变换为角求解;在最值问题和周期问题中,解题思路是合理运用基本公式将表达式转化为由一个三角函数表达的形式求解.4.立足课本、抓好基础.从前面表达可知,我们已经看到近几年高考已逐步抛弃了对复杂三角变换和特殊技巧的考查,而重点转移到对三角函数的图象与性质的考查,对基础知识和基本技能的考查上来,所以在复习中首先要打好基础.在考查利用三角公式进行恒等变形的同时,也直接考查了三角函数的性质及图象的变换,可见高考在降低对三角函数恒等变形的要求下,加强了对三角函数性质和图象的考查力度.四、复习建议本章内容由于公式多,且习题变换灵活等特点,建议同学们复习本章时应注意以下几点:(1)首先对现有公式自己推导一遍,通过公式推导了解它们的内在联系从而培养逻辑推理能力。
高考数学总复习教案:3.9三角函数的综合应用[ 高考]
![高考数学总复习教案:3.9三角函数的综合应用[ 高考]](https://img.taocdn.com/s3/m/c3b4bd3716fc700abb68fcc1.png)
第三章 三角函数、三角恒等变换及解三角形第9课时 三角函数的综合应用(对应学生用书(文)、(理)57~59页)1. (必修5P 9例题4题改编)设△ABC 的三个内角A 、B 、C 所对的边分别是a 、b 、c ,且a cosA =c sinC,则A =________.答案:π4解析:由a cosA =c sinC ,a sinA =c sinC ,得a sinA =acosA ,即sinA =cosA ,所以A =π4.2. (必修4P 45习题1.3第8题改编)将函数y =sinx 的图象向左平移φ(0≤φ<2π)个单位后,得到函数y =sin ⎝⎛⎭⎫x -π6的图象,则φ=________.答案:116π解析:将函数y =sinx 向左平移φ(0≤φ<2π)个单位得到函数y =sin(x +φ).只有φ=116π时有y =sin ⎝⎛⎭⎫x +116π=sin ⎝⎛⎭⎫x -π6. 3. (必修4P 109习题3.3第6(2)题改编)tan π12-1tan π12=________.答案:-23解析:原式=sinπ12cos π12-cosπ12sin π12=-⎝⎛⎭⎫cos 2π12-sin 2π12sin π12cos π12=-cosπ612sin π6=-2 3. 4. (必修4P 115复习题第13题改编)已知函数f(x)=3sinxcosx -cos 2x +12(x ∈R ),则f(x)在区间⎣⎡⎦⎤0,π4上的值域是________.答案:⎣⎡⎦⎤-12,32解析:f(x)=32sin2x -12cos2x =sin ⎝⎛⎭⎫2x -π6.当x ∈⎣⎡⎦⎤0,π4时,2x -π6∈⎣⎡⎦⎤-π6,π3,故值域为⎣⎡⎦⎤-12,32.5. 在△ABC 中,AC =7,BC =2,B =60°,则边BC 上的高为________. 答案:332解析:由余弦定理,得7=c 2+4-2c ,即c 2-2c -3=0,解得c =3,所以边BC 上的高h =3sin60°=332.1. 同角三角函数的基本关系式:sin 2α+cos 2α=1,tan α=sin αcos α.2. 两角和与差的正弦余弦和正切公式:sin (α±β)=sin αcos β±cos αsin β,cos (α±β)=cos αcos βsinαsin β,tan (α±β)=tan α±tan β1tan αtan β.3. 二倍角公式:sin2α=2sin αcos α,cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α,tan2α=2tan α1-tan 2α.4. 三角函数的图象和性质5. 正弦定理和余弦定理:(1) 正弦定理:a sinA =b sinB =csinC=2R(R 为三角形外接圆的半径).(2) 余弦定理:a 2=b 2+c 2-2bccosA ,cosA =b 2+c 2-a 22bc.题型1 三角恒等变换例1 已知sin ⎝⎛⎭⎫A +π4=7210,A ∈⎝⎛⎭⎫π4,π2.(1) 求cosA 的值;(2) 求函数f(x)=cos2x +52sinAsinx 的值域.解:(1) 因为π4<A<π2,且sin ⎝⎛⎭⎫A +π4=7210,所以π2<A +π4<3π4,cos ⎝⎛⎭⎫A +π4=-210.所以cosA =cos ⎣⎡⎦⎤⎝⎛⎭⎫A +π4-π4=cos ⎝⎛⎭⎫A +π4cos π4+sin ⎝⎛⎭⎫A +π4sin π4=-210·22+7210·22=35. (2) 由(1)可得sinA =45.所以f(x)=cos2x +52sinAsinx=1-2sin 2x +2sinx =-2⎝⎛⎭⎫sinx -122+32,x ∈R .因为sinx ∈[-1,1],所以,当sinx =12时,f(x)取最大值32;当sinx =-1时,f(x)取最小值-3. 所以函数f(x)的值域为⎣⎡⎦⎤-3,32. 备选变式(教师专享)(2013·上海卷)若cosxcosy +sinxsiny =12,sin2x +sin2y =23,则sin(x +y)=________.答案:23解析:由题意得cos(x -y)=12,sin2x +sin2y =sin[(x +y)+(x -y)]+sin[(x +y)-(x -y)]=2sin(x +y)cos(x-y)=23sin(x +y)=23.题型2 三角函数的图象与性质 例2 已知函数f(x)=Asin ⎝⎛⎭⎫π3x +φ,x ∈R ,A>0,0<φ<π2,y =f(x)的部分图象如图所示,P 、Q 分别为该图象的最高点和最低点,点P 的坐标为(1,A).(1) 求f(x)的最小正周期及φ的值;(2) 若点R 的坐标为(1,0),∠PRQ =2π3,求A 的值.解:(1) 由题意得T =2ππ3=6.因为P(1,A)在y =Asin ⎝⎛⎭⎫π3x +φ的图象上,所以sin ⎝⎛⎭⎫π3+φ=1.因为0<φ<π2,所以φ=π6.(2) 设点Q 的坐标为(x 0,-A). 由题意可知π3x 0+π6=3π2,得x 0=4,所以Q(4,-A).连结PQ ,在△PRQ 中,∠PRQ =2π3,由余弦定理得cos ∠PRQ =RP 2+RQ 2-PQ 22RP ·RQ =A 2+9+A 2-(9+4A 2)2A·9+A 2=-12,解得A 2=3.又A>0,所以A = 3. 备选变式(教师专享)已知函数f(x)=sin (ωx +φ)(ω>0,0≤φ≤π)为偶函数,且其图象上相邻两对称轴之间的距离为π. (1) 求函数f(x)的表达式;(2) 若sin α+f(α)=23,求2sin ⎝⎛⎭⎫2α-π4+11+tan α的值.解:(1) ∵ f(x)为偶函数,∴ sin(-ωx +φ)=sin (ωx +φ),即2sin ωxcos φ=0恒成立, ∴ cos φ=0,又∵ 0≤φ≤π,∴ φ=π2. 又其图象上相邻对称轴之间的距离为π,∴ T =2π,∴ ω=1,∴f(x)=cosx. (2) ∵ 原式=sin2α-cos2α+11+tan α=2sin αcos α,又∵ sin α+cos α=23,∴ 1+2sin αcos α=49, 即2sin αcos α=-59,故原式=-59.题型3 正弦定理、余弦定理的综合应用例3 (2013·浙江)在锐角△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,且2asinB =3b.(1) 求角A 的大小;(2) 若a =6,b +c =8,求△ABC 的面积.解:(1) 由2asinB =3b 及正弦定理a sinA =b sinB ,得sinA =32.因为A 是锐角,所以A =π3.(2) 由余弦定理a 2=b 2+c 2-2bccosA ,得b 2+c 2-bc =36.又b +c =8,所以bc =283. 由三角形面积公式S =12bcsinA ,得△ABC 的面积为733.备选变式(教师专享)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,C =π3,a =5,△ABC 的面积为10 3.(1) 求b ,c 的值; (2) 求cos ⎝⎛⎭⎫B -π3的值.解:(1) 由已知,C =π3,a =5,因为S △ABC =12absinC ,即103=12b ·5sin π3,解得b =8.由余弦定理可得:c 2=25+64-80cos π3=49, 所以c =7.(2) 由(1)有cosB =25+49-6470=17,由于B 是三角形的内角,易知sinB =1-cos 2B =437,所以cos ⎝⎛⎭⎫B -π3=cosBcos π3+sinBsin π3=17×12+437×32=1314.题型4 三角函数、平面向量、解三角形的综合应用例4 已知向量m =⎝⎛⎭⎫sinA ,12与n =(3,sinA +3cosA)共线,其中A 是△ABC 的内角. (1) 求角A 的大小;(2) 若BC =2,求△ABC 面积S 的最大值,并判断S 取得最大值时△ABC 的形状. 解:(1) 因为m ∥n ,所以sinA ·(sinA +3cosA)-32=0.所以1-cos2A 2+32sin2A -32=0,即32sin2A -12cos2A =1, 即sin ⎝⎛⎭⎫2A -π6=1.因为A ∈(0,π),所以2A -π6∈⎝⎛⎭⎫-π6,11π6. 故2A -π6=π2,A =π3.(2) 由余弦定理,得4=b 2+c 2-bc. 又S △ABC =12bcsinA =34bc ,而b 2+c 2≥2bcbc +4≥2bcbc ≤4(当且仅当b =c 时等号成立),所以S △ABC =12bcsinA =34bc ≤34×4= 3.当△ABC 的面积取最大值时,b =c. 又A =π3,故此时△ABC 为等边三角形.备选变式(教师专享)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ,设向量m =(a ,b),n =(sin B ,sin A),p =(b -2,a -2).(1) 若m ∥n ,求证:△ABC 为等腰三角形;(2) 若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积.(1) 证明:∵ m ∥n ,∴ asin A =bsin B ,即a·a 2R =b·b2R ,其中R 是△ABC 外接圆半径,∴ a =b.∴ △ABC为等腰三角形.(2) 解:由题意可知m·p =0,即a(b -2)+b(a -2)=0.∴ a +b =ab.由余弦定理可知,4=a 2+b 2-ab =(a +b)2-3ab ,即(ab)2-3ab -4=0,∴ab =4(舍去ab =-1),∴ S =12absin C =12×4×sin π3= 3.在已知值求角中,应合理选择三角函数形式进行求解,避免增根. 【示例】 (本题模拟高考评分标准,满分14分) 若sin α=55,sin β=1010,且α、β均为锐角,求α+β的值. 学生错解:解: ∵ α为锐角,∴ cos α=1-sin 2α=255.又β为锐角,∴ cos β=1-sin 2β=31010. ∵ sin (α+β)=sin αcos β+cos αsin β=22, 由于0°<α<90°,0°<β<90°, ∴ 0°<α+β<180°, 故α+β=45°或135°.审题引导: 在已知值求角中,角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能排除.要避免上述情况的发生,应合理选择三角函数形式进行求解,根据计算结果,估算出角的较精确的取值范围,并不断缩小角的范围,在选择三角函数公式时,一般已知正切函数值,选正切函数,已知正余弦函数值时,若角在(0,π)时,一般选余弦函数,若是⎝⎛⎭⎫-π2,π2,则一般选正弦函数.规范解答: 解: ∵ α为锐角,∴ cos α=1-sin 2α=255.(2分) 又β为锐角,∴ cos β=1-sin 2β=31010.(4分) 且cos (α+β)=cos αcos β-sin αsin β=22,(10分) 由于0<α<π2,0<β<π2,所以0<α+β<π,因为y =cosx 在[]0,π上是单调递减函数,故α+β=π4.(14分)错因分析: 没有注意挖掘题目中的隐含条件,忽视了对角的范围的限制,造成出错. 事实上,仅由sin (α+β)=22,0°<α+β<180°而得到α+β=45°或135°是正确的,但题设中sin α=55<12,sin β=1010<12,使得0°<α<30°,0°<β<30°从而0°<α+β<60°,故上述结论是错误的.在已知值求角中,应合理选择三角函数形式进行求解,避免增根.本题中0<α+β<π,因为y =cosx 在[]0,π上是单调函数,所以本题先求cos (α+β)不易出错.1. (2013·常州期末)函数f(x)=cos πx 2cos π(x -1)2的最小正周期为________.答案:2解析:f(x)=cos πx 2cos π(x -1)2=cos πx 2·sin πx 2=12sin πx ,最小正周期为T =2ππ=2.2. (2013·北京期末)已知函数f(x)=sin ⎝⎛⎭⎫x +π6,其中x ∈⎣⎡⎦⎤-π3,a ,若f(x)的值域是⎣⎡⎦⎤-12,1,则a 的取值范围是________.答案:⎣⎡⎦⎤π3,π 解析:若-π3≤x ≤a ,则-π6≤x +π6≤a +π6,因为当x +π6=-π6或x +π6=7π6时,sin ⎝⎛⎭⎫x +π6=12,所以要使f(x)的值域是⎣⎡⎦⎤-12,1,则有π2≤a +π6≤7π6,即π3≤a ≤π,即a 的取值范围是⎣⎡⎦⎤π3,π. 3. (2013·北京期末)已知△ABC 中,AB =3,BC =1,sinC =3cosC ,则△ABC 的面积为________. 答案:32解析:由sinC =3cosC ,得tanC =3>0,所以C =π3.根据正弦定理可得BC sinA =ABsinC ,即1sinA =332=2,所以sinA =12.因为AB>BC ,所以A<C ,所以A =π6,即B =π2,所以三角形为直角三角形,所以S △ABC =12×3×1=32.4. (2013·新课标Ⅰ卷)设当x =θ时,函数f(x)=sinx -2cosx 取得最大值,则cos θ=________. 答案:-255解析:∵ f(x)=sinx -2cosx =5⎝⎛⎭⎫55sinx -255cosx .令cos φ=55,sin φ=-255,则f(x)= 5(sinxcos φ+sin φcosx)=5sin(x +φ), 当x +φ=2k π+π2,k ∈Z ,即x =2k π+π2-φ,k ∈Z 时,f(x)取最大值,此时θ=2k π+π2-φ,k ∈Z ,∴ cos θ=cos ⎝⎛⎭⎫2k π+π2-φ=sin φ=-255.1. (2014·扬州期末)在锐角△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c.向量m =(1,cosB),n =(sinB ,-3),且m ⊥n .(1) 求角B 的大小;(2) 若△ABC 面积为103,b =7,求此三角形周长. 解:(1) m·n =sinB -3cosB ,∵ m ⊥n ,∴ m ·n =0, ∴ sinB -3cosB =0.∵ △ABC 为锐角三角形,∴ cosB ≠0, ∴ tanB = 3.∵ 0<B<π2,∴ B =π3.(2) ∵ S △ABC =12acsinB =34ac ,由题设34ac =103,得ac =40.由72=a 2+c 2-2accosB ,得49=a 2+c 2-ac ,∴ (a +c)2=(a 2+c 2-ac)+3ac =49+120=169.∴ a +c =13,∴ 三角形周长是20.2. 在△ABC 中, a 、b 、c 分别是角A 、B 、C 的对边,△ABC 的周长为2+2,且sinA +sinB =2sinC. (1) 求边c 的长;(2) 若△ABC 的面积为13sinC ,求角C 的度数.解:(1) 在△ABC 中, ∵ sinA +sinB =2sinC ,由正弦定理,得a +b =2c ,∴ a +b +c =2c +c =(2+1)c =2+2.∴ a +b =2,c = 2.(2) 在△ABC 中, S △ABC =12absinC =13sinC ,∴ 12ab =13 ,即ab =23. 又a +b =2,在△ABC 中,由余弦定理,得cosC =a 2+b 2-c 22ab =(a +b )2-2ab -22ab =12,又在△ABC中∠C ∈(0,π),∴ ∠C =60°.3. (2013·湖北卷)在△ABC 中,角A 、B 、C 对应的边分别是a 、b 、c.已知cos2A -3cos(B +C)=1. (1) 求角A 的大小;(2) 若△ABC 的面积S =53,b =5,求sinBsinC 的值.解:(1) 由已知条件得:cos2A +3cosA =1,∴ 2cos 2A +3cosA -2=0,解得cosA =12,∴ ∠A =60°.(2) S =12bcsinA =53c =4,由余弦定理,得a 2=21,(2R)2=a 2sin 2A =28,∴ sinBsinC =bc 4R 2=57.4. (2013·北京卷)在△ABC 中,a =3,b =26,∠B =2∠A. (1) 求cosA 的值; (2) 求c 的值.解:(1) 因为a =3,b =26,∠B =2∠A.所以在△ABC 中,由正弦定理得3sinA =26sin2A .所以2sinAcosAsinA =263.故cosA =63. (2) 由(1)知cosA =63,所以sinA =1-cos 2A =33. 又因为∠B =2∠A ,所以cosB =2cos 2A -1=13.所以sinB =1-cos 2B =223.在△ABC 中,sinC =sin(A +B)=sinAcosB +cosAsinB =539.所以c =sin sin a CA=5.1. 三角变换的基本策略是化异为同,即将函数名称、角、次数等化异为同.2. 对于函数y =Asin (ωx +φ)+B ,常用“五点法”画图象,运用整体思想研究性质.3. 求三角函数的单调区间、周期,及判断函数的奇偶性,要注意化归思想的运用,通过恒等变换转化为基本三角函数类型,注意变形前后的等价性.4. 解三角函数的综合题时应注意:(1) 与已知基本函数对应求解,即将ωx+φ视为一个整体X;(2) 将已知三角函数化为同一个角的一种三角函数,如y=Asin(ωx+φ)+B或y=asin2x+bsinx+c;(3) 换元方法在解题中的运用.请使用课时训练(B)第9课时(见活页).[备课札记]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章三角函数、三角恒等变换及解三角形第9课时三角函数的综合应用(对应学生用书(文)、(理)57~59页)考情分析考点新知理解和掌握同角三角函数的基本关系式、三角函数的图象和性质、两角和与差的正弦余弦与正切公式、二倍角公式及正弦定理和余弦定理,并能运用它们解决有关三角函数的综合问题.2. B级考点:① 同角三角函数的基本关系式②二倍角公式③三角函数的图象和性质④正弦定理和余弦定理1. (必修5P9例题4题改编)设△ABC的三个内角A、B、C所对的边分别是a、b、c,且acosA=csinC,则A=________.答案:π4解析:由acosA=csinC,asinA=csinC,得asinA=acosA,即sinA=cosA,所以A=π4.2. (必修4P45习题1.3第8题改编)将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位后,得到函数y=sin⎝⎛⎭⎫x-π6的图象,则φ=________.答案:116π解析:将函数y=sinx向左平移φ(0≤φ<2π)个单位得到函数y=sin(x+φ).只有φ=116π时有y =sin⎝⎛⎭⎫x+116π=sin⎝⎛⎭⎫x-π6.3. (必修4P109习题3.3第6(2)题改编)tanπ12-1tanπ12=________.答案:-2 3解析:原式=sinπ12cosπ12-cosπ12sinπ12=-⎝⎛⎭⎫cos2π12-sin2π12sinπ12cosπ12=-cosπ612sinπ6=-2 3.4. (必修4P115复习题第13题改编)已知函数f(x)=3sinxcosx -cos2x +12(x ∈R),则f(x)在区间⎣⎡⎦⎤0,π4上的值域是________.答案:⎣⎢⎡⎦⎥⎤-12,32解析:f(x)=32sin2x -12cos2x =sin ⎝⎛⎭⎫2x -π6.当x ∈⎣⎡⎦⎤0,π4时,2x -π6∈⎣⎡⎦⎤-π6,π3,故值域为⎣⎢⎡⎦⎥⎤-12,32. 5. 在△ABC 中,AC =7,BC =2,B =60°,则边BC 上的高为________. 答案:332解析:由余弦定理,得7=c2+4-2c ,即c2-2c -3=0,解得c =3,所以边BC 上的高h =3sin60°=332.1. 同角三角函数的基本关系式:sin2α+cos2α=1,tan α=sin αcos α.2. 两角和与差的正弦余弦和正切公式:sin (α±β)=sin αcos β±cos αsin β,cos (α±β)=cos αcos βsin αsin β,tan (α±β)=tan α±tan β1tan αtan β.3. 二倍角公式:sin2α=2sin αcos α,cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α,tan2α=2tan α1-tan2α.4. 三角函数的图象和性质5. 正弦定理和余弦定理:(1) 正弦定理:a sinA =b sinB =csinC =2R(R 为三角形外接圆的半径). (2)余弦定理:a2=b2+c2-2bccosA,cosA=b2+c2-a22bc.题型1 三角恒等变换例1 已知sin ⎝⎛⎭⎫A +π4=7210,A ∈⎝⎛⎭⎫π4,π2.(1) 求cosA 的值;(2) 求函数f(x)=cos2x +52sinAsinx 的值域.解:(1) 因为π4<A<π2,且sin ⎝⎛⎭⎫A +π4=7210,所以π2<A +π4<3π4,cos ⎝⎛⎭⎫A +π4=-210.所以cosA =cos ⎣⎡⎦⎤⎝⎛⎭⎫A +π4-π4=cos ⎝⎛⎭⎫A +π4cos π4+sin ⎝⎛⎭⎫A +π4sin π4=-210·22+7210·22=35. (2) 由(1)可得sinA =45. 所以f(x)=cos2x +52sinAsinx=1-2sin2x +2sinx =-2⎝⎛⎭⎫sinx -122+32,x ∈R.因为sinx ∈[-1,1],所以,当sinx =12时,f(x)取最大值32;当sinx =-1时,f(x)取最小值-3. 所以函数f(x)的值域为⎣⎡⎦⎤-3,32.备选变式(教师专享)(2013·上海卷)若cosxcosy +sinxsiny =12,sin2x +sin2y =23,则sin(x +y)=________. 答案:23解析:由题意得cos(x -y)=12,sin2x +sin2y =sin[(x +y)+(x -y)]+sin[(x +y)-(x -y)]=2sin(x +y)cos(x -y)=23sin(x +y)=23.题型2 三角函数的图象与性质例2 已知函数f(x)=Asin ⎝⎛⎭⎫π3x +φ,x ∈R ,A>0,0<φ<π2,y =f(x)的部分图象如图所示,P 、Q 分别为该图象的最高点和最低点,点P 的坐标为(1,A).(1) 求f(x)的最小正周期及φ的值;(2) 若点R 的坐标为(1,0),∠PRQ =2π3,求A 的值.解:(1) 由题意得T =2ππ3=6.因为P(1,A)在y =Asin ⎝⎛⎭⎫π3x +φ的图象上,所以sin ⎝⎛⎭⎫π3+φ=1. 因为0<φ<π2,所以φ=π6. (2) 设点Q 的坐标为(x0,-A). 由题意可知π3x0+π6=3π2,得x0=4, 所以Q(4,-A).连结PQ ,在△PRQ 中,∠PRQ =2π3,由余弦定理得 cos ∠PRQ =RP2+RQ2-PQ22RP ·RQ =A2+9+A2-(9+4A2)2A·9+A2=-12,解得A2=3.又A>0,所以A = 3.备选变式(教师专享)已知函数f(x)=sin (ωx +φ)(ω>0,0≤φ≤π)为偶函数,且其图象上相邻两对称轴之间的距离为π.(1) 求函数f(x)的表达式;(2) 若sin α+f(α)=23,求2sin ⎝⎛⎭⎫2α-π4+11+tan α的值.解:(1) ∵ f(x)为偶函数,∴ sin(-ωx +φ)=sin (ωx +φ),即2sin ωxcos φ=0恒成立, ∴ cos φ=0,又∵ 0≤φ≤π,∴ φ=π2. 又其图象上相邻对称轴之间的距离为π,∴ T =2π, ∴ ω=1,∴f(x)=cosx.(2) ∵ 原式=sin2α-cos2α+11+tan α=2sin αcos α,又∵ sin α+cos α=23,∴ 1+2sin αcos α=49,即2sin αcos α=-59,故原式=-59 . 题型3 正弦定理、余弦定理的综合应用例3 (2013·浙江)在锐角△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,且2asinB =3b. (1) 求角A 的大小;(2) 若a =6,b +c =8,求△ABC 的面积.解:(1) 由2asinB =3b 及正弦定理a sinA =b sinB ,得sinA =32.因为A 是锐角,所以A =π3. (2) 由余弦定理a2=b2+c2-2bccosA ,得b2+c2-bc =36.又b +c =8,所以bc =283. 由三角形面积公式S =12bcsinA ,得△ABC 的面积为733. 备选变式(教师专享)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,C =π3,a =5,△ABC 的面积为10 3. (1) 求b ,c 的值;(2) 求cos ⎝⎛⎭⎫B -π3的值.解:(1) 由已知,C =π3,a =5,因为S △ABC =12absinC , 即103=12b ·5sin π3,解得b =8.由余弦定理可得:c2=25+64-80cos π3=49, 所以c =7.(2) 由(1)有cosB =25+49-6470=17,由于B 是三角形的内角,易知sinB =1-cos2B =437,所以cos ⎝⎛⎭⎫B -π3=cosBcos π3+sinBsin π3=17×12+437×32=1314. 题型4 三角函数、平面向量、解三角形的综合应用例4 已知向量m =⎝⎛⎭⎫sinA ,12与n =(3,sinA +3cosA)共线,其中A 是△ABC 的内角.(1) 求角A 的大小;(2) 若BC =2,求△ABC 面积S 的最大值,并判断S 取得最大值时△ABC 的形状. 解:(1) 因为m ∥n ,所以sinA ·(sinA +3cosA)-32=0. 所以1-cos2A 2+32sin2A -32=0, 即32sin2A -12cos2A =1, 即sin ⎝⎛⎭⎫2A -π6=1.因为A ∈(0,π),所以2A -π6∈⎝⎛⎭⎫-π6,11π6.故2A -π6=π2,A =π3.(2) 由余弦定理,得4=b2+c2-bc. 又S △ABC =12bcsinA =34bc , 而b2+c2≥2bcbc +4≥2bcbc ≤4(当且仅当b =c 时等号成立),所以S △ABC =12bcsinA =34bc≤34×4= 3. 当△ABC 的面积取最大值时,b =c. 又A =π3,故此时△ABC 为等边三角形.备选变式(教师专享)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ,设向量m =(a ,b),n =(sin B ,sin A),p=(b -2,a -2).(1) 若m ∥n ,求证:△ABC 为等腰三角形;(2) 若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积.(1) 证明:∵ m ∥n ,∴ asin A =bsin B ,即a·a 2R =b·b2R ,其中R 是△ABC 外接圆半径,∴ a =b.∴ △ABC 为等腰三角形. (2) 解:由题意可知m·p =0,即a(b -2)+b(a -2)=0.∴ a +b =ab.由余弦定理可知,4=a2+b2-ab =(a +b)2-3ab ,即(ab)2-3ab -4=0,∴ab =4(舍去ab =-1), ∴ S =12absin C =12×4×sin π3= 3.在已知值求角中,应合理选择三角函数形式进行求解,避免增根. 【示例】 (本题模拟高考评分标准,满分14分)若sin α=55,sin β=1010,且α、β均为锐角,求α+β的值. 学生错解:解: ∵ α为锐角,∴ cos α=1-sin2α=255. 又β为锐角,∴ cos β=1-sin2β=31010. ∵ sin (α+β)=sin αcos β+cos αsin β=22,由于0°<α<90°,0°<β<90°, ∴ 0°<α+β<180°, 故α+β=45°或135°.审题引导: 在已知值求角中,角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能排除.要避免上述情况的发生,应合理选择三角函数形式进行求解,根据计算结果,估算出角的较精确的取值范围,并不断缩小角的范围,在选择三角函数公式时,一般已知正切函数值,选正切函数,已知正余弦函数值时,若角在(0,π)时,一般选余弦函数,若是⎝⎛⎭⎫-π2,π2,则一般选正弦函数. 规范解答: 解: ∵ α为锐角,∴ cos α=1-sin2α=255.(2分) 又β为锐角,∴ cos β=1-sin2β=31010.(4分) 且cos (α+β)=cos αcos β-sin αsin β=22,(10分) 由于0<α<π2,0<β<π2,所以0<α+β<π,因为y =cosx 在[]0,π上是单调递减函数,故α+β=π4.(14分)错因分析: 没有注意挖掘题目中的隐含条件,忽视了对角的范围的限制,造成出错.事实上,仅由sin(α+β)=2 2,0°<α+β<180°而得到α+β=45°或135°是正确的,但题设中sinα=55<12,sinβ=1010<12,使得0°<α<30°,0°<β<30°从而0°<α+β<60°,故上述结论是错误的.在已知值求角中,应合理选择三角函数形式进行求解,避免增根.本题中0<α+β<π,因为y=cosx在[]0,π上是单调函数,所以本题先求cos(α+β)不易出错.1. (2013·常州期末)函数f(x)=cosπx2cosπ(x-1)2的最小正周期为________.答案:2解析:f(x)=cosπx2cosπ(x-1)2=cosπx2·sinπx2=12sinπx,最小正周期为T=2ππ=2.2. (2013·北京期末)已知函数f(x)=sin⎝⎛⎭⎫x+π6,其中x∈⎣⎡⎦⎤-π3,a,若f(x)的值域是⎣⎡⎦⎤-12,1,则a的取值范围是________.答案:⎣⎡⎦⎤π3,π解析:若-π3≤x≤a,则-π6≤x+π6≤a+π6,因为当x+π6=-π6或x+π6=7π6时,sin⎝⎛⎭⎫x+π6=12,所以要使f(x)的值域是⎣⎡⎦⎤-12,1,则有π2≤a+π6≤7π6,即π3≤a≤π,即a的取值范围是⎣⎡⎦⎤π3,π.3. (2013·北京期末)已知△ABC中,AB=3,BC=1,sinC=3cosC,则△ABC的面积为________.答案:32解析:由sinC=3cosC,得tanC=3>0,所以C=π3.根据正弦定理可得BCsinA=ABsinC,即1sinA=332=2,所以sinA=12.因为AB>BC,所以A<C,所以A=π6,即B=π2,所以三角形为直角三角形,所以S△ABC=12×3×1=32.4. (2013·新课标Ⅰ卷)设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=________.答案:-255解析:∵f(x)=sinx-2cosx=5⎝⎛⎭⎪⎫55sinx-255cosx.令cosφ=55,sinφ=-255,则f(x)=5(sinxcosφ+sinφcosx)=5sin(x+φ),当x +φ=2k π+π2,k ∈Z ,即x =2k π+π2-φ, k ∈Z 时,f(x)取最大值,此时θ=2k π+π2-φ,k ∈Z , ∴ cos θ=cos ⎝⎛⎭⎫2k π+π2-φ=sin φ=-255.1. (2014·扬州期末)在锐角△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c.向量m =(1,cosB),n =(sinB ,-3),且m ⊥n. (1) 求角B 的大小;(2) 若△ABC 面积为103,b =7,求此三角形周长. 解:(1) m·n =sinB -3cosB ,∵ m ⊥n ,∴ m ·n =0, ∴ sinB -3cosB =0.∵ △ABC 为锐角三角形,∴ cosB ≠0,∴ tanB = 3.∵ 0<B<π2,∴ B =π3.(2) ∵ S △ABC =12acsinB =34ac ,由题设34ac =103,得ac =40.由72=a2+c2-2accosB ,得49=a2+c2-ac ,∴ (a +c)2=(a2+c2-ac)+3ac =49+120=169.∴ a +c =13, ∴ 三角形周长是20.2. 在△ABC 中, a 、b 、c 分别是角A 、B 、C 的对边,△ABC 的周长为2+2,且sinA +sinB =2sinC.(1) 求边c 的长;(2) 若△ABC 的面积为13sinC ,求角C 的度数.解:(1) 在△ABC 中, ∵ sinA +sinB =2sinC ,由正弦定理,得a +b =2c ,∴ a +b +c =2c +c =(2+1)c =2+2. ∴ a +b =2,c = 2.(2) 在△ABC 中, S △ABC =12absinC =13sinC , ∴ 12ab =13 ,即ab =23.又a +b =2,在△ABC 中,由余弦定理,得cosC =a2+b2-c22ab =(a +b )2-2ab -22ab =12,又在△ABC 中∠C ∈(0,π), ∴ ∠C =60°. 3. (2013·湖北卷)在△ABC 中,角A 、B 、C 对应的边分别是a 、b 、c.已知cos2A -3cos(B +C)=1.(1) 求角A 的大小;(2) 若△ABC 的面积S =53,b =5,求sinBsinC 的值.解:(1) 由已知条件得:cos2A +3cosA =1,∴ 2cos2A +3cosA -2=0,解得cosA =12,∴ ∠A =60°.(2) S =12bcsinA =53c =4,由余弦定理,得a2=21,(2R)2=a2sin2A =28,∴ sinBsinC =bc4R2=57.4. (2013·北京卷)在△ABC 中,a =3,b =26,∠B =2∠A. (1) 求cosA 的值; (2) 求c 的值.解:(1) 因为a =3,b =26,∠B =2∠A.所以在△ABC 中,由正弦定理得3sinA =26sin2A .所以2sinAcosA sinA =263.故cosA =63.(2) 由(1)知cosA =63,所以sinA =1-cos2A =33.又因为∠B =2∠A ,所以cosB =2cos2A -1=13.所以sinB =1-cos2B =223. 在△ABC 中,sinC =sin(A +B)=sinAcosB +cosAsinB =539.所以c =sin sin a CA =5.1. 三角变换的基本策略是化异为同,即将函数名称、角、次数等化异为同.2. 对于函数y =Asin (ωx +φ)+B ,常用“五点法”画图象,运用整体思想研究性质.3. 求三角函数的单调区间、周期,及判断函数的奇偶性,要注意化归思想的运用,通过恒等变换转化为基本三角函数类型,注意变形前后的等价性.4. 解三角函数的综合题时应注意:(1) 与已知基本函数对应求解,即将ωx +φ视为一个整体X ;(2) 将已知三角函数化为同一个角的一种三角函数,如y =Asin (ωx +φ)+B 或y =asin2x +bsinx +c ;(3) 换元方法在解题中的运用.请使用课时训练(B)第9课时(见活页).[备课札记]。
