温度应力计算
温度应力计算·
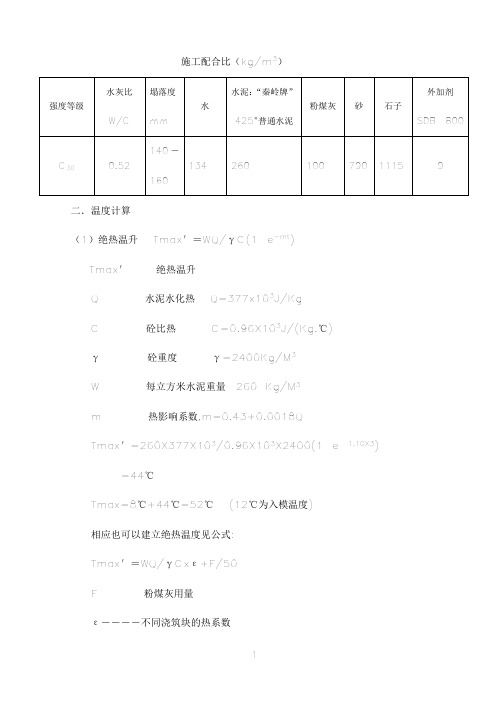
施工配合比（kg/m3）二．温度计算（1）绝热温升Tmax′＝WQ/γC(1-e-mt) Tmax′---绝热温升Q-----水泥水化热Q=377x103J/KgC-----砼比热C=0.96X103J/(Kg.℃)γ-----砼重度γ=2400Kg/M3W-----每立方米水泥重量260 Kg/M3m-----热影响系数,m=0.43+0.0018QTmax′=260X377X103/0.96X103X2400(1-e-1.10X3) =44℃Tmax=8℃+44℃=52℃(12℃为入模温度)相应也可以建立绝热温度见公式:Tmax′＝WQ/γCxε+F/50F-----粉煤灰用量ε――――不同浇筑块的热系数Tmax′＝260X377X103/Tmax=8+55=63℃取Tmax＝63℃三. 温应力计算1.将砼的收缩随时间的进程换算成当量温度计算：Ty(t)= εy(t)/αα=1x10-5砼线膨胀系数εy(t)=ε0M1M2M3······M10(1-e0.01t)Ty(t)------当量温度εy(t)----任意时间的收缩(mm/mm)M1-----水泥品种为普通水泥,取1.0M2-----水泥细度为4000孔，取1.35M3-----骨料为石灰石，取1.00M4-----水灰比为0.52,取1.64M5-----水泥浆量为0.2,取1.00M6------自然养护30天，取0.93M7------环境相对湿度为50%,取0.54M8------水里半径倒数为0.4,取1.2M9------机械振捣，取1.00M10------含筋率为8%,取0.9ε0--ε∞---最终收缩，在标准状态下ε0=3.24X10-4εy(30)=1.01x10-4Ty(30)=10.1℃εy(27)=0.92 x10-4Ty(27)=9.2℃εy(24)=0.83 x10-4Ty(24)=8.3℃εy(21)=0.73 x10-4 Ty(21)=7.3℃εy(18)=0.64 x10-4Ty(18)=6.4℃εy(15)=0.54 x10-4Ty(15)=5.4℃εy(12)=0.439 x10-4 Ty(12)=4.39℃εy(9)=0.335 x10-4 Ty(9)=3.35℃εy(6)=0.226 x10-4 Ty(6)=2.26℃εy(3)=0.114 x10-4 Ty(3)=1.14℃计算中心温度当量温差:△T6=2.26-1.14=1.12℃△T9=3.35-2.26=1.09℃△T12=4.39-3.35=1.04℃△T15=5.4-4.39=1.01℃△T18=6.4-5.4=1.0℃△T21=7.3-6.4=0.9℃△T24=8.3-7.3=1.0℃△T27=9.2-8.3=0.9℃△T30=10.1-9.2=0.9℃2.计算中心温度砼基础施工时处于散热条件，考虑上下表面及侧面的散热条件,当体积厚达3m时,,散热影响系数取0.97；当中心浇筑完第四天后，水化热达峰值。
门刚pkpm温度应力计算
门刚pkpm温度应力计算门刚PKPM温度应力计算主要包括以下几个步骤：1. 计算门刚的热膨胀系数,常用的门刚材料热膨胀系数为11.7 × 10^-6 m/(m·K)。
2. 计算门刚的温度增量,温度增量等于实际温度减去参考温度。
例如,如果实际温度为200℃,参考温度为20℃,则温度增量为180℃。
3. 根据线膨胀系数计算门的线膨胀量,线膨胀量等于门刚的长度乘以热膨胀系数和温度增量的乘积。
例如,如果门刚的长度为1米,热膨胀系数为11.7 × 10^-6 m/(m·K),温度增量为180℃,则线膨胀量为1 × 11.7 × 10^-6 × 180 = 0.002106米。
4. 根据门的横截面积计算门的面积膨胀量,面积膨胀量等于门的横截面积乘以热膨胀系数和温度增量的乘积。
例如,如果门的横截面积为1平方米,热膨胀系数为11.7 × 10^-6 m/(m·K),温度增量为180℃,则面积膨胀量为1 × 11.7 × 10^-6 × 180 = 0.002106平方米。
5. 根据门的长度和横截面积计算门的体积膨胀量,体积膨胀量等于门的长度乘以横截面积乘以热膨胀系数和温度增量的乘积。
例如,如果门的长度为1米,横截面积为1平方米,热膨胀系数为11.7 × 10^-6 m/(m·K),温度增量为180℃,则体积膨胀量为1 × 1 × 11.7 × 10^-6 × 180 = 0.002106立方米。
6. 根据门的材料特性和受力情况,在门的横截面上进行应力计算,根据材料的弹性模量和应变,计算门在温度变化下产生的应力。
需要注意的是,在进行温度应力计算时,需要考虑到门在受力过程中可能会发生塑性变形,因此需要进行综合考虑计算。
混凝土温度应力控制标准
混凝土温度应力控制标准一、前言混凝土在使用过程中，由于受到外界环境的影响和内部物理化学过程的作用，会产生一定的应力。
其中，混凝土温度应力是一个常见的问题。
混凝土温度应力主要是由于混凝土在硬化过程中由于收缩而产生的，同时也会受到外界环境温度变化的影响。
因此，为了保证混凝土的稳定性和使用寿命，需要进行温度应力的控制。
二、标准概述混凝土温度应力控制标准是为了保证混凝土在使用过程中的稳定性和安全性而制定的。
该标准主要针对混凝土温度应力的控制要求进行了详细的规定，包括温度应力的计算方法、控制标准的要求、监测方法等方面。
该标准适用于各种混凝土结构的设计、施工和使用过程中的温度应力控制。
三、标准内容1. 温度应力的计算方法混凝土温度应力的计算方法主要包括两种：一种是基于混凝土收缩应力的计算方法，另一种是基于混凝土温度变化引起的应力的计算方法。
其中，基于混凝土收缩应力的计算方法主要针对混凝土在硬化过程中由于收缩而产生的应力进行计算，而基于混凝土温度变化引起的应力的计算方法主要针对混凝土在使用过程中由于温度变化而产生的应力进行计算。
在具体计算时，应根据混凝土的材料性质、结构设计要求和使用环境等方面进行综合考虑，选择合适的计算方法进行计算。
2. 控制标准的要求混凝土温度应力的控制标准主要包括两个方面：一是对温度应力的限制，二是对混凝土结构的变形控制。
具体要求如下：（1）对温度应力的限制混凝土温度应力的限制应根据具体结构的设计要求和使用环境等方面进行综合考虑，选择合适的限制标准。
一般来说，混凝土温度应力的限制应不超过混凝土的抗拉强度的10%。
（2）对混凝土结构的变形控制混凝土结构的变形控制应根据具体结构的设计要求和使用环境等方面进行综合考虑，选择合适的变形控制标准。
一般来说，混凝土结构的变形控制应不超过结构设计要求的变形控制标准。
3. 监测方法混凝土温度应力的监测方法主要包括两种：一种是基于传感器的实时监测方法，另一种是基于观察和测量的定期监测方法。
2019年温度场和温度应力计算.doc
附计算书3：温度场和温度应力计算一、温度场计算计算以本工程1.2m 厚底板为例，用差分法计算底板28d 水化热温升曲线。
计算中各参数的取值如下：W ——每m 3胶凝材料用量，440kg/ m 3；Q ——胶凝材料水化热总量（kJ/kg ）；，本例采用实测值260kJ/kg ；c ——混凝土的比热，取1.0kJ/ (kg ∙C )；ρ——混凝土的质量密度，取2400kg/ m 3；α——导温系数，取0.0035m 2/h ；m ，取0.5。
混凝土的入模温度取10C ，地基温度为18C ，大气温度为18C 。
温度场计算差分公式如下：1,1,,1,,222(21)2n k n kn k n kn k T T t t T aT a T x x -+++∆∆=∙--+∆∆∆ （B.4.2-1）⑴试算t ∆、x ∆，确定2x t∆∆α。
取t ∆ = 0.5天 = 12小时，x ∆ = 0.4m ，即分3层 则412625.04.0120035.022≈=⨯=∆∆x t α，可行。
代入该值得出相应的差分法公式为k k n kn k n k n T T T T T ∆+⋅++⋅=+-+,,1,11,475.02525.0⑵画出相应的计算示意图，并进行计算。
底板厚1.2m ，分3层，每层0.4m ，相应的计算示意如下图。
从上至下各层混凝土的温度分别用1T 、2T 、3T 表示，相应k 时刻各层的温度即为k T ,1、k T ,2、k T ,3。
混凝土与大气接触的上表面边界温度用0T 表示，与地基接触的下表面边界温度用0'T 表示。
k = 0，即第05.00=⋅=∆⋅t k 天， 上表面边界0T ，取大气温度，0T = 18C 各层混凝土温度取入模温度，即0,1T =0,2T = 0,3T = 10C下表面边界0'T ，取地基温度，0'T = 18C ；k = 1，即第5.05.01=⋅=∆⋅t k 天，温升=-⋅⋅⋅=-=∆⋅⋅-⋅-⋅-∆⋅⋅-∆⋅-⋅-)(24000.1260440)(5.015.05.0)11(5.0)1(max 1e e e eT T t k m tk m10.544C上表面边界温度0T ，散热温升为0，始终保持不变，0T = 18C第一层混凝土温度1,1T ，见计算图示中方框1，1,1T 的边界为0T 和0,2T ，在0,1T 的基础上考虑温升1T ∆，即C T T T T T 644.22475.02525.010,10,201,1=∆+⋅++⋅=第二层混凝土温度1,2T ，见计算图示中方框2，1,2T 的边界为0,1T 和0,3T ，在0,2T 的基础上考虑温升1T ∆，即C T T T T T 544.20475.02525.010,20,30,11,2=∆+⋅++⋅=m m m第三层混凝土温度1,3T ，见计算图示中方框3，1,3T 的边界为0,2T 和0'T ，在0,3T 的基础上考虑温升1T ∆，即2,003,13,010.5250.47522.6442T T T T T C'+=+⋅+∆=︒下表面边界温度0'T ，需要考虑散热温升2/1T ∆，所以需每一步都需进行修正。
超长大体积混凝土浇筑体施工阶段温度应力与收缩应力的计算方法
超长大体积混凝土浇筑体施工阶段温度应力与收缩应力的计算方法1 混凝土的绝热温升1.1水泥的水化热可按下列公式计算：01t Q Q t n t =+（1. 1-1）00t t n t Q Q Q =+（1. 1-2） 07347/3/Q Q Q =-（1. 1-3）式中t Q —龄期t 时的累积水化热（kJ/kg ）0Q —水泥水化热总量（kJ/kg ）t —龄期（t ）n —常数，随水泥品种、比表面积等因素不同而异1.2胶凝材料水化热总量应在水泥、掺合料、外加剂用量确定后根据实际配合比通过实验得出。
当无实验数据时，可按下式计算：0kQ Q =（1.2）式中Q —胶凝材料水化热总量（kJ/kg ）k —不同掺量掺合料水化热调整系数1.3当现场采用粉煤灰与矿渣粉双掺时，不同掺量掺合料水化热调整系数可按下式计算：121-+=k k k （1.3）式中1k —粉煤灰掺量对应的水化热调整系数可按表1.3取值2k —矿渣粉掺量对应的水化热调整系数可按表1.3取值表1.3 不同掺量掺合料水化热调整系数注：表中掺量为掺合料占总胶凝材料的百分比1.4混凝土的绝热温升值可按下式计算：()(1)mt WQ T t e C ρ-=-（1.4）式中()t T —龄期为t 时，混凝土的绝热升温（℃）W —每立方米混凝土的胶凝材料用量（kg/m 3）C —混凝土比热容，可取（0.92~1.0）(kJ/kg·℃）ρ—混凝土的质量密度，可取（2400~2500）（kg/m 3） m —与水泥品种、浇筑温度等有关的系数，可取（0.3~0.5）d -1t —龄期（d ）2 混凝土收缩值的当量温度2.1混凝土收缩的相对变形量可按下式计算：00.0112311()(1)t y y t e M M M M εε-=-⨯⨯⨯⋅⋅⋅（2.1）式中)(t y ε—龄期为t 时，混凝土收缩引起的相对变形值yε—在标准试验状态下混凝土最终收缩的相对变形值，取3.24×10-4 1121M M M ⋅⋅⋅—混凝土收缩值不同条件影响修正系数，可按表2.1取值2.2 混凝土收缩相对变形值的当量温度可按下式计算:()αε/)(t t T y y = (2.2)式中)(t T y —龄期为t 时,混凝土收缩当量温度；α—混凝土的线性膨胀系数,取1.0×10-5。
工程的温度应力计算
工程的温度应力计算文件管理序列号：[K8UY-K9IO69-O6M243-OL889-F88688]一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（0.0+2.4+6.4+11.9+17.0+20.9+24.4+25.2+22.1+16.9+9.2+3.5）/12=13.3。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
表1 2000年~2009年青岛月平均气温只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
混凝土面层温度应力计算公式
混凝土面层温度应力计算公式引言：混凝土是一种常用的建筑材料，具有良好的耐久性和承载能力。
然而，在使用过程中，混凝土受到温度变化的影响，可能会产生应力。
因此，了解混凝土面层温度应力的计算公式是非常重要的，可以帮助我们评估混凝土结构的安全性和稳定性。
一、混凝土面层温度应力的原因和影响因素混凝土面层的温度应力主要是由于温度变化引起的材料膨胀或收缩不均匀导致的。
温度的变化会导致混凝土发生体积变化，从而产生内部应力。
以下是影响混凝土面层温度应力的主要因素：1. 温度变化幅度：温度变化幅度越大，混凝土面层的温度应力就越大。
2. 混凝土材料的热膨胀系数：不同的混凝土材料具有不同的热膨胀系数，热膨胀系数越大，温度应力越大。
3. 混凝土的约束条件：混凝土的约束程度越大，温度应力越大。
4. 混凝土的几何形状和结构：不同的混凝土结构和几何形状对温度应力的分布和大小有影响。
二、混凝土面层温度应力的计算公式混凝土面层温度应力的计算公式可以通过考虑混凝土的热膨胀和约束情况来推导得出。
一种常用的计算公式是线膨胀系数法，其计算公式如下：ΔL = α × L × ΔT其中，ΔL为混凝土面层的长度变化，α为混凝土的线膨胀系数，L 为混凝土的初始长度，ΔT为温度变化。
温度应力可以通过以下公式计算：σ = E × ΔL / L其中，σ为混凝土面层的温度应力，E为混凝土的弹性模量，ΔL为混凝土面层的长度变化，L为混凝土的初始长度。
三、混凝土面层温度应力的计算实例为了更好地理解混凝土面层温度应力的计算过程，我们来看一个简单的实例。
假设一个混凝土面层的初始长度为10m，温度变化为50℃，混凝土的线膨胀系数为12×10^-6/℃，弹性模量为30 GPa。
根据线膨胀系数法计算混凝土面层的长度变化：ΔL = α × L × ΔT= 12×10^-6/℃ × 10m × 50℃= 0.006m然后，根据温度应力的计算公式计算混凝土面层的温度应力：σ = E × ΔL / L= 30 GPa × 0.006m / 10m= 18 MPa因此，根据以上计算，该混凝土面层在温度变化为50℃时，将产生18 MPa的温度应力。
某工程的温度应力计算
一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（0.0+2.4+6.4+11.9+17.0+20.9+24.4+25.2+22.1+16.9+9.2+3.5）/12=13.3。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6.1混凝土施工裂缝控制6.1.1混凝土温度的计算
①混凝土浇筑温度:T
j =T
c
+(T
q
-T
c
)×(A
1
+A
2
+A
3
+……+A
n
)
式中：T
c
—混凝土拌合温度（℃），按多次测量资料，在没有冷却措施的条件下，有日照时混凝土拌合温度比当时温度高5-7 ℃，无日照时混凝土拌
合温度比当时温度高2-3 ℃，我们按3 ℃计；、
T
q
—混凝土浇筑时的室外温度（考虑最夏季最不利情况以30 ℃计）；
A 1、A
2
、A
3
……A
n
—温度损失系数，A
1
—混凝土装、卸，每次A=0.032(装
车、出料二次)；A
2
—混凝土运输时，A=θt查文献[5]P
33表3-4得6 m3滚动式搅拌车运输θ=0.0042，运输时
间t约30分钟，A=0.0042×30=0.126；A
3
—浇捣过程中A=0.003t, 浇捣时间t约240min, A=0.003×
240=0.72；
T j =33+(T
q
-T
c
)×(A
1
+A
2
+A
3
)=33+(30-33)×(0.032×2+0.126+0.72) =33+（-3）×0.91=30.27 ℃
②混凝土的绝热温升：T(t)=W×Q×（1-e-mt）/（C×r）
式中：T(t)—在t龄期时混凝土的绝热温升（℃）；
W—每m3混凝土的水泥用量（kg/m3），取350kg/m3；
Q—每公斤水泥28天的累计水化热(KJ/kg), 采用425号矿渣水泥Q =335kJ/kg(文献[5] P
14
表2-1)；
C—混凝土比热0.97 KJ/(kg·K) ；
r—混凝土容重2400 kg/m3；
e—常数，2.71828；
m—与水泥品种、浇筑时温度有关，可查文献[5]P
35
表3-5；
t—混凝土龄期（d）。
混凝土最高绝热温升T
h
=W×Q/（C×r）=350×335/(0.97×2400)=50.37（℃）
③混凝土内部中心温度：T
max (t)=T
j
+ T
1
(t)
式中：T
max
(t)—t龄期混凝土内部中心温度；
T
j
—混凝土浇筑温度（℃）；
ξ—不同浇筑块厚度的温降系数，查文献[5]P 44表3-8得，对3 m 厚混凝
土3天时ξ=0.68；
T 1(t)—混凝土内部水泥水化热的平均温升，T 1(t)=T(t)×ξ。
T 1= T h ×ξ=50.37×0.68=34.25（℃）
混凝土内部中心温度T max (3)=T j + T 1=30.27+34.25=64.52（℃）
从混凝土温度计算得知,在混凝土浇筑后第三天混凝土内部温度64.5℃,比室外温度(30℃)高出34.5℃,必须采用相应的措施,防止大体积钢筋混凝土承台因温差过大产生裂缝。
6.1.2温度应力计算 （1）桥台承台温度应力
桥台承台H/L=1.5/12.19=0.12<0.2,按一维弹性地基上的长条板计算由温差和混凝土收缩所产生的温度应力σmax ：
σmax =-EaT[1-1/(ch βL/2)]S(t)
式中：E —混凝土各龄期时对应的弹性模量E t =E c （1-e -0.09t ）；
t-混凝土龄期（天数）；
E c —龄期为28天时混凝土的弹性模量，C 30，E t =3.0×104 MPa ； a —混凝土的线膨胀系数1.0×10-5/℃； T —结构计算温差；
L —结构长度，桥台承台长度L=12.19m ； ch β—是双曲余弦函数, β=HE
C x
=
β，H 为结构厚度； C x —阻力系数(即产生单位位移的剪应力）(N/mm 3),目前主要是参考土动力
学、抗滑稳定试验等方面的理论研究和统计资料，C x 取值为： 软粘土 0.01~0.03 N/mm 3
； 砂质粘土 0.03~0.06 N/mm 3； 坚硬粘土 0.06~0.10 N/mm 3； 风化岩石和低强度等级素混凝土 0.60~1.00 N/mm 3； C10以上的配筋混凝土 1.00~1.50 N/mm 3； S(t)—混凝土应力松弛系数，)1()1(1)(21221
1t P t P e P A
e P A t S ------
=，经验
系数11023701.0-=d A 、1245167.3-=d A 、1
1067419.0-=d
P 、1243797.9-=d P 。
采用桩基时，桩对结构的变形亦有约束作用，所以除去上述地基的阻力系数外，尚需增加单位面积地基上桩的阻力系数'x C ：
F
Q
C x =
'
式中Q ―桩产生单位位移所需的水平力（N/mm ）；
当桩与结构铰接时3
4
)4(2EI D K EI Q n =, 当桩与结构固接时3
4
)4(4EI
D K EI Q n = F ―每根桩分担的地基面积（mm 2）； Kn ―地基水平侧移刚度（1×10－2N/ mm 2）；
E ―桩的弹性模量（MPa ）； I ―桩的惯性矩（mm 4）； D ―桩的直径或边长（mm ）。
结构计算温差T ，可按下式计算：T = Tm + Ty(t)
式中Tm ―各龄期混凝土的水泥水化热降温温差（℃），可用混凝土浇筑后因水泥
水化热的升温值来确定水泥水化热降温温差Tm ； Ty(t)―各龄期的混凝土的收缩当量温差（℃ ）。
Tm ＝ T 2＋1/2（T 1 －T 2），其中T 2为混凝土结构表面因水泥水化热而升高的温度数值，)(''
22)(4t q T h H h H
T T ∆-+
=；龄期t 时，混凝土中心温度与外界气温之差)(t T ∆= T max (t)- q T ；混凝土结构的虚厚度'h =K λ/β，折减系数K=0.666，混凝土导热系数λ=2.33W/(m ·K),β为混凝土表面模板及保温层等的传热系数(W ／(m 2·K)，β按下式计算：∑+=
q
i i β
λδβ1
1
，空气层传热系数q β=23 W ／m 2·K ，
i δ为各保温材料（包括模板）的厚度（m ），i λ为各保温材料的导热系数，可查文献[5]P 52表3-11。
混凝土各龄期的收缩当量温差，按下式计算: α
ε)
()(t t T y y =
； 混凝土各龄期的收缩值10210
)1()(M M M e t bt y y ⋅⋅⋅⋅⋅⋅⋅⋅-=-εε；
0y ε―标准状态下混凝土的极限收缩值，一般为3.24 ×10－4 ；
b ―经验系数，取0.01； t ―混凝土龄期（d ）；
1021M M M ⋅⋅⋅⋅⋅⋅⋅―修正系数,具体数值见文献[5]P 65表4－1。