四色定理的证明范文
“四色定理”简捷证明(完整版)

“四色定理”简捷证明王若仲(王洪)贵州省务川自治县实验学校贵州564300摘要:1852年,毕业于伦敦大学的格斯里(FrancisGuthrie)来到一家科研单位搞地图着色工作时,发现每幅地图都可以只用四种颜色着色。
这个现象能不能从数学上加以严格证明呢?1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题,世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜想证明的进程。
就在1976年6月,在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿判断,结果没有一张地图是需要五色的,最终证明了四色定理。
我发现“四色定理”还有一种简捷的证明方法,就是利用球面几何的知识来证明“四色定理”。
关键词:四色定理;球面几何;线段;相交中图分类号:0156引言1852年,毕业于伦敦大学的格斯里(FrancisGuthrie)来到一家科研单位搞地图着色工作时,发现每幅地图都可以只用四种颜色着色。
这个现象能不能从数学上加以严格证明呢?他和他正在读大学的弟弟决心试一试,但是稿纸已经堆了一大叠,研究工作却是没有任何进展。
1852年10月23日,他的弟弟就这个问题的证明请教了他的老师、著名数学家德·摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密顿爵士请教,但直到1865年哈密顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题,世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
1878~1880年两年间,著名的律师兼数学家肯普(Alfred Kempe)和泰勒(Peter Guthrie Tait)两人分别提交了证明四色猜想的论文,宣布证明了四色定理。
四色定理简要证明论文

四色定理的简要证明摘要:文章严格遵循数学归纳法步骤,利用数学归纳法和平面图的一个定理成功证明了世界近代三大数学难题之一的四色定理,并献疑于该定理的“计算机证明”。
关键词:数学归纳法;证明;平面图;四色定理中图分类号:g633.6文献标识码:a 文章编号:1002-7661(2011)11-045-01“画地图要求相邻两国不用同一色,一幅地图只需要四种颜色”(钱学森语),这就是著名的“四色定理”(或称“四色问题”)。
自1872年正式提出至1976年才被计算机证明,但这“机证”并非让所有人信服。
下面给出一种非“机证”的简洁的理论证明。
一、相关前提前提1任何平面地图的着色问题可以转化、归纳为对平面图的结点的着色问题。
其中的结点代表地图上的国家(或地区,下同),结点间的连线即边代表国家间的相邻关系。
前提2着色规则——平面图内有连线(即边,下同,为叙述方便会交替使用)的点(即结点,下同)必须用不同种的颜色着色,而没有连线的点则肯定可以用同一种颜色着色。
前提3“正常着色”是指遵守“前提2”所称着色规则的着色。
前提4设g是有v个结点e条边的连通简单平面图,若v>=3,则e=3),都适用e=5)时,定理成立,即可用4种色对图g(k)正常着色,亦即可用4色对k个结点正常着色。
那么,当n=k+1时,对这(k+1)个结点着色,必定可分两步进行:第一步,首先对其中的k个结点着色;第二步,才对剩下的“1”个结点(称为第n点,n=k+1)着色。
已知k个点可用4色正常着色,不难证明第n点也可以用这 4色中的某一色正常着色。
其理由是:当n=k时,图g(k)共有结点个数为:v(k)=k(a);边数据“前提4”为:e(k)<=3v-6=3k-6(b)当n=k+1时,有图g(k+1),此时g(k+1)的结点个数为:v(k+1)=k+1(c);边数则为:e(k+1)<=3v-6=3(k+1)-6=(3k-6)+3 (d)因为:(c)-(a)=(k+1)-k=1,(d)-(b)<=(3k-6)+3-(3k-6)<=3所以可确知:图g(k+1)比图g(k)仅增加1个结点(即第n点)及最多增加3条边,所增加的3条边是增加的第n点所引致,两者具有对应关系。
四色定理的简单证明
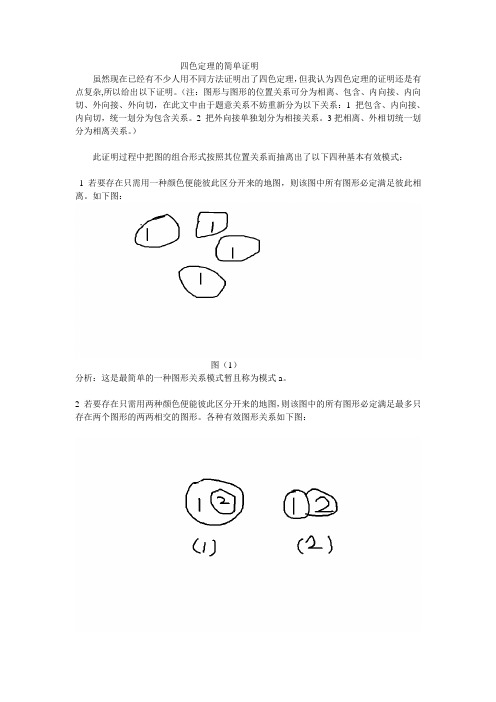
四色定理的简单证明虽然现在已经有不少人用不同方法证明出了四色定理,但我认为四色定理的证明还是有点复杂,所以给出以下证明。
(注:图形与图形的位置关系可分为相离、包含、内向接、内向切、外向接、外向切,在此文中由于题意关系不妨重新分为以下关系:1 把包含、内向接、内向切,统一划分为包含关系。
2 把外向接单独划分为相接关系。
3把相离、外相切统一划分为相离关系。
)此证明过程中把图的组合形式按照其位置关系而抽离出了以下四种基本有效模式:1 若要存在只需用一种颜色便能彼此区分开来的地图,则该图中所有图形必定满足彼此相离。
如下图:图(1)分析:这是最简单的一种图形关系模式暂且称为模式a。
2 若要存在只需用两种颜色便能彼此区分开来的地图,则该图中的所有图形必定满足最多只存在两个图形的两两相交的图形。
各种有效图形关系如下图:图(2)分析:两个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系模式之一。
由于图(1)存在包含关系,被包含的图形是对外部无影响的,所以图(1)仍属于模式a。
所以两个图形的两两相交只有图(2)的相交关系模式的图形有效的,我们暂且称之为模式b。
3 若要存在只需用三种颜色便能彼此区分开来的地图,则给图中所有图形必定满足最多只存在三个图形的两两相交图形。
各种有效图形关系如下图:图(3)分析:三个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系模式之一。
由于图(2)属于存在包含关系,同理整体回归于模式a。
所以三个图形的两两相交只有图(1)的相接关系模式的图形是有效图形模式,我们暂且称之为模式c。
4 若要存在只需用四种颜色便能彼此区分开来的地图,则给图中所有图形必定满足最多只存在四个图形的两两相交图形。
各种有效图形关系如下图:图(4)分析:四个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系。
由于图(2)属于存在包含关系,同理可得出整体也就回归于图形模式a。
趣味数学故事之关于“四色问题”的证明-教育文档

趣味数学故事之关于“四色问题”的证明趣味数学故事之关于“四色问题”的证明“四色问题”是世界数学史上一个非常著名的证明难题,它要求证明在平面地图上只要用四种颜色就能使任何复杂形状的各块相邻区域之间颜色不会重复,也就是说相互之间都有交界的区域最多只能有四块。
一百五十多年来有许多数学家用了很长时间,化了很多精力才能证明这个问题。
前些日子报刊上曾有报道说:有好几位大学生用好几台电子计算机联合起来化了十几个小时才证明了这个问题。
本人在二十多年前就知道有这么一个“四色问题”,可一直找不到证明它的方法。
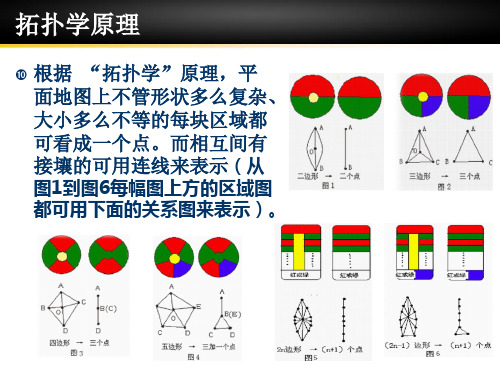
现在我刚接触到“拓扑学”,其实用“拓扑学”原理一分析,“四色问题”就象当年欧拉把“七桥问题”看成是经过四个点不重复的七条线段的“一笔画”一样简单,连一般的小学生都能证明它。
根据“拓扑学”原理,任何复杂形状的每一块区域都可看成是一个点,两块区域之间相互有交界的可看成这两点之间有连线,只要证明在一个平面内,相互之间都有连线的点不会超过四个,也就证明了“四色问题”。
平面内的任意一个点A可与许许多多的点B、C、D……X、Y、Z有连线(如图1所示),同样B点也可与其它点有连线,C、D……X、Y、Z各点也可与其它点有连线。
但有一个原则:各连线之间不能相互交叉,因为一旦交叉就会产生一条连线隔断另一条连线(如图2所示),BC的连线就隔断了AD的连线。
但有人会说:两点间的连线可有许多条,AD连线可绕到B点或C点以外(图2中虚线所示)不就没有交叉了吗?可是这样一绕就产生一个结果:原来在一个封闭图形外的点变成了封闭图形内的点。
下面就通过对封闭图形的分析来证明相互之间都有连线的点不超过四个。
一个点本身或两个点之间的连线都可形成一个或多个封闭图形(如图3所示)。
三个相互之间都有连线的点从A点连到B点再到C点又回到A点(如图4所示),必定会造成图形的封闭。
封闭图形上的点若多于四点(如图5所示),从第三点C起各点与第一点A的连线又将整个封闭图形分割成许多小的封闭图形。
四色定理的终极证明证明篇
公共边现象
在去掉中间点的过程中,很 容易出现连成一串的四边形 (如图8中的B和C都是四边形 的中心点),可先去掉B点把 C与A合并,也可先去掉C点把 D与B合并。从A点到D点实际 上是两个多边形的公共边, 在去掉这些四边形中心点的 过程中,因为有着依次去掉 一个合并一个的规律,可一 次性把这些点去掉,A到D的 总点数是单数,合并后只剩 下A点;A到D的总点数是双数, 合并后只剩下A和D两点。
公共边现象 图8
精品课件!
精品课件!
四色定理终极证明的说明
•一偶然机会,看到一篇《简单明了的四色问题的证明》,作者是焦永溢。这 个证明很有条理,又简单易懂,但是证明方法是否正确呢?我向许多数学爱 好者、数学教授专家求证,理会的人不多。据悉作者本人焦永溢也给众多数 学家、专家教授发过N多邮件,基本石沉大海。
如图3所示,由于上与下区域不接 壤可用同一种颜色、左与右区域也 不接壤也可用同一种颜色,所以中 间区域只要用第三种颜色就行了。 由于中间区域只与周围四个区域有 接壤,不与外界其它区域有接壤, 所以它的存在与否,只要外围四区 域着色不变也不会影响其它区域的 着色。就是说:在整个最大平面图 中可把图3中左边的情况看成与右 边的一样(图中是中间用了绿色使 左右区域相连,也可以用红色使上 下区域相连),下方的关系图就是 去掉中心O点,把C点合并到B点, 只剩下三个点二条线。
五个区பைடு நூலகம்包围一个区域的情况
如图4所示,周围五个区域中, A与C可用同一种颜色,B与E可 用另一种颜色,D就必须用第三 种颜色,而中心的O就需要用第 四种颜色。由于中间区域与以 上几种情况一样只与包围它的 五个区域有接壤,它的存在与 否,只要外围五区域着色不变 也不会影响其它区域的着色。 就是说:在整个最大平面图中 可把图4中左边的情况看成与右 边一样,下方的关系图就是去 掉中心O点,把E点合并到B点, 只剩下四个点四条线。
四色定理的证明

四色定理的证明《四色定理的证明》“哇,你看这个地图好漂亮啊!”我兴奋地对同桌小明说。
那是一节平常的数学课,老师在讲台上讲着各种图形知识,我和小明却偷偷对着一张世界地图看得出神。
“嘿,你说要是给每个国家都涂上颜色,最少需要几种颜色就能让相邻的国家颜色不一样呢?”我好奇地问小明。
小明挠挠头:“这可不好说,感觉挺复杂的呢。
”就在我们讨论得热火朝天的时候,老师的声音传来:“你们俩在嘀咕什么呢!”我们赶紧坐好,假装认真听课。
但我的思绪却一直停留在那个地图和颜色的问题上。
回到家,我迫不及待地开始研究起来。
我找了好多张纸,画了各种奇奇怪怪的图形,然后试着给它们涂色。
“哎呀,怎么这么难啊!”我有点懊恼。
这时妈妈走了过来,看着我乱七八糟的纸,笑着问:“宝贝,你这是在干嘛呀?”我把我的想法告诉了妈妈,妈妈鼓励我说:“这可是个很有意思的问题呢,你别着急,慢慢想。
”我继续埋头苦干,在经过无数次尝试后,我突然发现好像四种颜色真的就够了!“哇塞,我好像有点眉目了!”我兴奋地大喊。
第二天我赶紧跑去和小明分享我的发现,小明惊讶地说:“真的吗?你太厉害了!”于是我们俩又开始一起深入研究,我们不断地讨论、验证。
“你看,这个图形这样涂色就可以只用四色。
”我得意地对小明说。
“哇,还真是,那其他的呢?”小明追问。
就这样,我们在不断地探索中越来越坚信四色定理是真的。
我不禁想,这看似简单的四色定理,背后却蕴含着这么多的思考和努力,就像我们的学习和生活一样,很多事情不经过一番努力和探索,怎么能知道其中的奥秘呢?这不就是像攀登一座高峰,只有一步步往上爬,才能看到最美的风景吗?我相信,只要我们保持这份好奇和探索的精神,就没有什么难题是解决不了的!四色定理不就是最好的证明吗?。
最终被计算机所证明的百年数学难题——四色定理

和费马大定理,庞加莱猜想一样, 四色定理 也是那种叙述起来非常简单,证明起来却极其困难的百年数学难题。
但四色定理非常特殊的一点在于,它的最终证明并不是传统的数学逻辑证明,而是借助计算机分析所有可能的情形后完成的。
这也就是说,四色定理的证明迄今为止仍非单独的人力所能及,我们仍然没有找到理论上的逻辑证明,但借助计算机强大的计算能力,的确又可以解决这个难题。
四色猜想四色猜想最早并不是由职业数学家提出的,而是由从事地图制作的 费兰西斯.古色利(Francis Gurthire)发现的。
在为不同的地图着色过程中,细心的古色列发现,对于相邻(具有公共边界)的地区,若它们着不同颜色,那么只要四种颜色就可以完成这张地图。
好奇心强烈的古色列对这个猜想的正确性非常感兴趣,但苦于自己不具备专业的数学知识,于是他将这个问题告诉了自己在伦敦大学学数学的弟弟 费雷德里克·古色利(Frederick Guthrie),但弟弟也无能为力,后来他又寻求老师,著名数学家 德·摩根(deMorgan,1806~1871,提出了集合论中著名的德·摩根定律) 的帮助。
但令兄弟二人震惊的是,即使是德·摩根这样出色的数学家也对这个问题无能为力。
德·摩根但德·摩根算得上是四色猜想的第一位先驱,实际上他证明了至少需要四种颜色,并且因此留下了关于四色猜想最早的正式文字记录。
同样,德·摩根向许多当时著名的数学家咨询过这个问题,但都一无所获,直到英国著名数学家 凯莱(ArthurCayley,1821~1895,矩阵论创始人) 在1878年向伦敦数学会提交这个问题后,四色猜想才开始广为人知,并吸引了众多数学家来研究这个问题。
凯莱在凯莱正式向数学界提出四色猜想后不到一年时间内,毕业于剑桥大学数学系的律师 肯普(Kempe)给出了一个看似正确的证明,但直到十一年后, 希伍德(Heawood) 才发现了肯普证明中的错误,由此证明四色猜想的努力再次破产。
四色定理证明方法

四色定理证明方法全文共四篇示例,供读者参考第一篇示例:四色定理是数学上一个非常重要的定理,它指出任何一个地图都可以用四种颜色进行着色,使得相邻的区域彼此颜色不同。
这个定理虽然看似简单,但却是一个深奥的数学问题,其证明方法也非常复杂。
四色定理最早由英国数学家弗朗西斯·加思顿在1852年提出,并且在1976年由美国数学家凯尼思·阿普尔和沃夫冈·哈肯证明。
这个定理的证明方法主要是通过图论和逻辑推理来完成。
我们来介绍一下四色定理的一些基本概念。
在地图着色问题中,地图可以看作是由一些区域和它们之间的边界组成的。
而一个合法的地图着色方案就是给每个区域都分配一种颜色,使得相邻的区域颜色不同。
四色定理的证明方法涉及到很多复杂的数学理论,其中最主要的是图论。
图论是一门研究图和网络结构的数学学科,它在证明四色定理中起着至关重要的作用。
在证明四色定理时,数学家们首先将地图转化为一个特殊的图的形式,这个图被称为地图的双图。
地图的双图是在地图的基础上构造出来的一个图,在这个图中每个区域对应一个顶点,而边界对应一条连接这两个顶点的边。
这样一来,地图的问题就被转化为图的问题。
为了证明四色定理,数学家们需要证明对于任意一个地图的双图,我们都可以使用四种颜色进行着色。
证明的关键在于通过逻辑推理来排除一些特殊情况,使得我们只需要考虑一些简单的情况。
数学家们通过对图的结构和特性进行分析和归纳,最终找到了一种方法来证明四色定理的真实性。
除了图论,证明四色定理还涉及到概率论、逻辑推理和计算机算法等领域的知识。
数学家们通过将不同学科的知识相结合,从不同角度来审视这个问题,最终找到了证明四色定理的方法。
四色定理的证明方法是一个集合多种数学技巧和理论的综合性问题,它不仅考验数学家们的数学功底和逻辑思维能力,同时也展示了数学的复杂性和魅力。
四色定理虽然已经被证明,但它依然是数学领域中一个重要而且有趣的问题,相信在未来会有更多数学家对这个问题进行深入的研究和探索。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四色定理的证明范文
一、四色问题的简介
根据网络上的一些内容,可知:
四色猜想是说,任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。
也就是说,在不引起混淆的情况下,一张地图只需四种颜色来标记就行。
用数学语言来说就是,将平面任意地细分为不相重叠的区域,每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。
简单来说也就是,给平面或球面上的任意一张地图上色,使得相邻国家异色,那么至少需要预备几种颜料几种颜色?是否可以只预备四种颜色?
在长期的论证过程中,人们发现,大量的试涂表明,四种颜色够用。
人们证明,三种颜色是不够用的,五种颜色肯定够用,四种颜色也够用(计算机证明)。
人们还证明,二维平面内无法构造五个或五个以上两两相邻区域。
在四色问题中
假设相邻关系是指两个国家有一段或多段共同边界,是指有邻边,不是指有邻点。
假设没有公地,所有国家都直接接壤(分别相邻),或者间接接壤(分别相连)。
假设没有飞地,国土连通。
飞地相当于任意指定一些他国属于国,则四色肯定不够用了。
假设国家的面积都足够大,不是一丁点、一个点。
假设国家的数量有限,不是无限多。
假设国家的形状任意。
这可以是五花八门,变化莫测,花样繁多,譬
如像麋鹿的剪影:
在四色问题中
需要考虑任意地带的上下方面的相邻情况,左右方面的相邻情况,内
外方面的相邻情况,首尾衔接(例如圆周中)的相邻情况,跨越跳跃(例
如国形状像拱桥、麋鹿、藤蔓、交际花,与诸多位置的国家们接壤)着的
相邻情况,等等。
需要考虑各国的排序,需要考虑上色的顺序。
因为许多国家相邻相连,交织交错,来来往往,层层叠叠,那么从多个方向来上色的话,齐头并进
来上色的话,就会互相遭遇、碰头,在交汇点上可能发生冲突,难以协调、确定国的颜色,使得问题复杂,影响证明的进行。
二、四色定理的证明
一个平面或球面上的点是无限小、无限多,或者是足够小、非常多。
令这些点各自随机选择红黄蓝三色的一种,再做布朗运动。
运动时间随机,但是不能过长或过短。
运动中,颜色相同的点相遇后就粘结在一起,形成
色斑、色块。
运动结束后,那些零星零散的足够小的色点色斑被吸附,被
改色,融入附近的色块。
这样一来,这个平面或球面就被分割成红黄蓝三
色的若干色块,其中相邻的色块肯定颜色不同,也就是构造出了三色地图。
上述的过程可以反复进行,无限进行,就构造出了三色地图的无限丰
富的素材库、成品库。
同样,随机选择红黄蓝绿四种颜色,就构造出了四色地图及其无限丰
富的素材库、成品库。
同样,随机选择赤橙黄绿青五种色,就构造出了五色地图及其无限丰
富的素材库、成品库。
已知三色不够用,三色地图仅是特例之类,已知五色够用,那么四色
是够用还是不够用呢?
如果任一五色地图可以改涂成四色,就证明四色有充分的可行性。
如果任一地图不需要用五种及更多颜色来上色,就证明四色够用。
将任一五色地图(赤橙黄绿青),改涂成四色地图(红黄蓝绿),这
有充分的可行性吗?
首先,可以将五色地图中的橙黄绿青改涂成白色,赤色保持不变,各
国的国界保持不变。
那么这些赤色之间没有相邻,
那么这些白色只有二种可能:与一个或多个赤色有相邻,或者无相邻。
如果一个白色与赤色没有相邻,那就把它再改涂成赤色。
多个白色相
连与赤色没有相邻,就从中选择一个或多个,改成赤色。
总之,就是说,用赤色和白色给所有国家上色,使得任一白色与一个
或多个赤色有相邻,使得赤色之间没有相邻,使得赤色尽量的多,使得赤
色及其白色邻国涵盖所有的国家,其中,赤色的都是独立一国,白色的是
多国共用白色。
此时就任一赤色来看,它的邻国全是白色。
假设这些白色邻国多于四
个(或者一个,二个,或三、四个等)。
那么从这些白色邻国中任意抽取四个则没有两两相邻。
假若有,一定
能再次改涂,将其中一个改涂成赤色。
也就是说,任意抽取、反复抽取四个白色邻国,它们顶多使用三色即可。
除非它们两两相邻,才需要四色。
此时就任一赤色来看,它的邻国全是白色。
假设这些白色邻国多于四
个(或者一个,二个,或三、四个等)。
那么从这些白色邻国中任意抽取三个,与这一赤色之间要么有两两相邻,要么没有。
也就是说,任意抽取、反复抽取三个白色邻国,它们与赤色用四色即可。
此时就任一白色来看,它的邻国是白色和赤色。
假设这些邻国多于四
个(或者一个,二个,或三、四个等)。
此时这一白色的邻国,可能分属多个赤色圈子。
多个赤色圈子中的赤
白二色的若干个国家是这一白色的邻国。
那么从这一白色和其白色邻国来看,顶多三色就可以进行改涂。
那么从这一白色和其赤白邻国来看,顶多四色就可以进行改涂。
以上也就是说,任一五色地图进行改涂的话,任一地图进行上色的话,顶多使用四色即可。
亦即,四色具备充分可行性。
在这里,如何上色就不讨论了,能否上色成功也不讨论了。
不需要讨论,可以不进行讨论。
综上可得:
由于四色具备了充分可行性,
由于四色地图具备了存在性,
由于四色地图的素材库、成品库具备了无限丰富性,
那么针对平面或球面上的任一地图来说,四色总是够用,总是可以上
色成功。
证毕。
三、一些说明
上述的证明过程是这样:
1,论证任一赤橙黄绿青的五色地图(或者尚未上色的任一地图),
能够暂时改涂为赤白二色。
2,论证任一赤白二色的地图,顶多需要四色来做终极改涂。
这证明
了四色有充分的可行性,但是还没有证明必定上色成功。
3,论证四色地图有存在性,且有无限的丰富性,从而证明了四色有
充分的可行性,并且还具有上色成功的必然性。
4,得证。
两两相邻的国家不会有五个,大家知道这个结论很关键,可是这个已
经被证明的结论不能直接证明四色定理,需要找出一些关键的东西之后,
才能够拿着去证明四色定理。
如何拿着它去证明四色定理呢?这里的做法,是先把任一地图用赤白二色来上色,进而展示出地图上任何一个地方不会
超出四色。
此时还没有得出证明,引入四色地图的存在性和无限丰富性,
就得证了。
在一个赤色的各个白色邻国当中,或者所有赤色的所有白色邻国当中,假若必须使用四种颜色来给这些白色国家改涂、上色,那么必定存在两两
相邻的四个白色。
也就是说,对任意一个白色,不需要看它有多少个白色
邻国,只需要看它和其他的任意的三个白色,能否形成两两相邻的四个白色。
如果它这个白色,和其他的任意三个白色,能够形成两两相邻的四个
白色,则就需要使用四种颜色来改涂,来上色。
如果它这个白色,和其他
的任意三个白色,不能形成两两相邻的四个白色,则不需要使用四种颜色
来改涂,来上色。
亦即,在所有白色当中随机抽取四个、反复抽取四个即可,并不需要抽取更多。
那么两两相邻的四个白色不存在。
这也是说,顶多有三个白色是两两
相邻(占用黄蓝绿),并且第四个白色顶多与三个中的二个都相邻。
亦即
第四个白色顶多与三个中的二个(设用黄蓝)都相邻,和另一个白色(设
用绿色)不相邻。
则第四个白色也用绿色即可,合计黄蓝绿三色。
由于任一赤色的所有白色邻国顶多使用黄蓝绿三色,即可完成终极改
涂
由于任一白色的所有白色邻国顶多使用黄蓝绿三色,即可完成终极改
涂
那么赤色和黄蓝绿合计是四种,就是红黄蓝绿四色。
顶多使用四色,
就可以把赤白二色的任一地图做终极改涂,改涂后地图上任意两个邻国异色。
