编译原理第3章答案
《编译原理教程》课后习题答案第三章语法分析

第三章 语法分析
3.10 已知文法G[A]: A→aABl|a B→Bb|d
(1) 试给出与G[A]等价的LL(1)文法G[A′]; (2) 构造G[A′]的LL(1)分析表; (3) 给出输入串aadl#的分析过程。 【解答】 (1) 文法G[A]存在左递归和回溯,故其不是 LL(1)文法。要将G[A]改造为LL(1)文法,首先要消除文法 的左递归,即将形如P→Pα | β 的产生式改造为 P→β P′ P→α P′| ε
对A′→ABl来说, FIRST(A)∩FOLLOW(A′)={a}∩{#,d}=Φ ,所以文法 G′[A]为所求等价的LL(1)文法。
第三章 语法分析
(2) 构造预测分析表的方法如下: ① 对文法G[A′]的每个产生式A→α 执行②、③ 步。 ② 对 每 个 终 结 符a∈FIRST(A) ,把 A→α 加 入 到 M[A,a]中,其中α 为含有首字符a的候选式或为唯一的 候选式。 ③ 若ε ∈FIRST(A),则对任何属于FOLLOW(A)的 终结符b,将A→ε 加入到M[A,b]中。把所有无定义的 M[A,a]标记上“出错”。 由此得到G[A′]的预测分析表,见表3-1。
c. 最左推导和最右推导必定相同
d. 可能存在两个不同的最左推导,但它们对应的语法树 相同
第三章 语法分析
(3) 采用自上而下分析,必须 。
a. 消除左递归
b. 消除右递归
c. 消除回溯
d. 提取公共左因子
(4) 设a、b、c是文法的终结符,且满足优先关系 ab和bc,则 。
编译原理第三章练习题答案

编译原理第三章练习题答案一、选择题1. 在编译原理中,词法分析器的作用是什么?A. 将源代码转换为汇编代码B. 将源代码转换为中间代码C. 识别源代码中的词法单元D. 检查源代码的语法正确性答案:C2. 词法单元中,标识符和关键字的区别是什么?A. 标识符可以重定义,关键字不可以B. 标识符和关键字都是常量C. 标识符是用户自定义的,关键字是语言预定义的D. 标识符和关键字都是变量名答案:C3. 下列哪个不是词法分析器生成的属性?A. 行号B. 列号C. 词法单元的类型D. 词法单元的值答案:A4. 词法分析器通常使用哪种数据结构来存储词法单元?A. 栈B. 队列C. 链表D. 数组答案:C5. 词法分析器的实现方法有哪些?A. 手工编写正则表达式B. 使用词法分析器生成器C. 编写扫描程序D. 所有上述方法答案:D二、简答题1. 简述词法分析器的基本工作流程。
答案:词法分析器的基本工作流程包括:读取源代码字符,根据正则表达式匹配词法单元,生成词法单元的类型和值,并将它们作为输出。
2. 什么是正规文法?它在词法分析中有什么作用?答案:正规文法是一种形式文法,它使用正则表达式来定义语言的词法结构。
在词法分析中,正规文法用于描述程序设计语言的词法规则,帮助词法分析器识别和生成词法单元。
三、应用题1. 给定一个简单的词法分析器,它需要识别以下词法单元:标识符、关键字(如if、while)、整数、运算符(如+、-、*、/)、分隔符(如逗号、分号)。
请描述该词法分析器的实现步骤。
答案:实现步骤如下:- 定义词法单元的类别和对应的正则表达式。
- 读取源代码字符,逐个字符进行匹配。
- 使用状态机或有限自动机来识别词法单元。
- 根据匹配结果生成相应的词法单元类型和值。
- 输出识别的词法单元。
2. 设计一个简单的词法分析器,它可以识别以下C语言关键字:int, float, if, else, while, return。
蒋立源编译原理第三版第三章习题与答案(修改后)
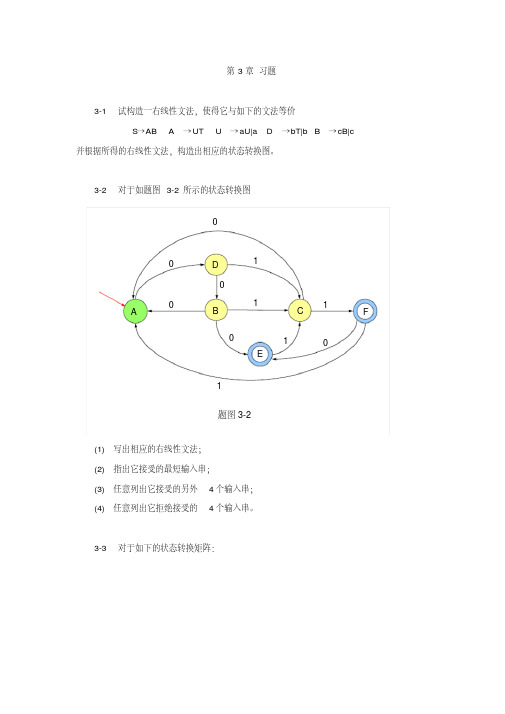
3-1 试构造一右线性文法,使得它与如下的文法等价 S→AB A → UT U → aU|a D →bT|b B → cB|c
并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图 3-2 所示的状态转换图 0
0 0 A
D
1
0 1
B
C1
F
0
1
0
E
1 题图 3-2
(1) 写出相应的右线性文法; (2) 指出它接受的最短输入串; (3) 任意列出它接受的另外 4 个输入串; (4) 任意列出它拒绝接受的 4 个输入串。
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(3) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(3) 之 (a) 所示, 给各状态重新命名,即令:
[S]=1, [A]=2, [S,B]=3 且由于 3 的组成中含有 M的终态 B,故 3 为 DFAM′的终态。于是,所构造之 DFAM′的 状态转换矩阵和状态转换图如答案图 3-4-(3) 之(b) 及(c) 所示。
π0:{1,2}, {3}
( ⅱ) 为得到下一分划,考察子集 {1,2} 。因为
{2} b ={3}
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(4) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(4) 之 (a) 所示, 给各状态重新命名,即令:
编译原理教程-课后习题答案第三章语法分析ppt课件

a. LALR文法 b. LR(0)文法
c. LR(1)文法 d. SLR(1)文法
第三章 语法分析
(8) 同心集合并有能够产生新的 冲突。
a. 归约
b. “移进〞/“移进〞
c.“移进〞/“归约〞 〞
d. “归约〞/“归约
【解答】 (1) c (2) a (3) c (5) b (6) b (7) d (8) d
#⋖ (⋖,⋖ (⋖a⋗)⋗)⋗# 因此,素短语为a。
第三章 语法分析
3.8 下述文法描画了C言语整数变量的声明语句: G[D]: D→TL T→int|long|short L→id|L,id
(1) 改造上述文法,使其接受一样的输入序列, 但文法是右递归的;
(2) 分别用上述文法G[D]和改造后的文法G[D′] 为输入序列int a,b,c构造分析树。
第三章 语法分析
(2) 为了构造字母表Σ={a,b}上同时只需奇数个a 和奇数个b的一切串集合的正规式,我们画出如图3-3 所示的DFA,即由开场符S出发,经过奇数个a到达形状 A,或经过奇数个b到达形状B;而由形状A出发,经过 奇数个b到达形状C(终态);同样,由形状B出发经过奇 数个a到达终态C。
第三章 语法分析
第三章 语法分析
3.1 完成以下选择题:
(1) 文法G:S→xSx|y所识别的言语是 。
a. xyx
b. (xyx)*
c. xnyxn(n≥0)
d. x*yx*
(2) 假设文法G是无二义的,那么它的任何句子α 。
a. 最左推导和最右推导对应的语法树必定一样
b. 最左推导和最右推导对应的语法树能够不同 c. 最左推导和最右推导必定一样
能否不画出语法树,而直接由定义(即在句型中)寻觅满足某 个产生式的候选式这样一个最左子串(即句柄)呢?例如,对句型 aAaBcbbdcc,我们可以由左至右扫描找到第一个子串AaB,它恰好 是满足A→AaB右部的子串;与树(a)对照,AaB确实是该句型的句 柄。能否这一方法一直正确呢?我们继续检查句型aAcbBdcc,由 左至右找到第一个子串c,这是满足A→C右部的子串,但由树(b) 可知,c不是该句型的句柄。由此可知,画出对应句型的语法树然 后寻觅最左直接短语是确定句柄的好方法。
编译原理 第二版 第三章课后答案

第三章作业第三章作业答案P47 练习1、文法G=({A,B,S},{a,b,c},P,S),其中P为:S->Ac|aB A->ab B->bc写出L(G [S])的全部元素。
S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}2、文法G[N]为:N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?【解】N=>ND=>NDD.... =>NDDDD...D=>D......DG[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}或:解: N ND n-1D n{0,1,3,4,5,6,7,8,9}+∴L(G[N])= {0,1,3,4,5,6,7,8,9}+5.写一文法,使其语言是偶正数的集合。
要求:(1)允许0打头(2)不允许0打头【解】(1)允许0开头的偶正整数集合的文法E->NT|G|SFMT->NT|GN->D|1|3|5|7|9D->0|GG->2|4|6|8S->NS|εF->1|3|5|7|9|GM->M0|0(2)不允许0开头的偶正整数集合的文法E->NT|DT->FT|GN->D|1|3|5|7|9D->2|4|6|8F->N|0G->D|09.考虑下面上下文无关文法:S→SS*|SS+|a(1) 表明通过此文法如何生成串aa+a*,并为该串构造推导树。
(2) 该文法生成的语言是什么?【解】(1) S=>SS*=>SS+S*aa+a*该串的推导树如下:(2) 该文法生成的语言是只含+、*的算术表达式的逆波兰表示。
11.令文法G[E]为:E→T|E+T|E-TT→F|T*F|T/FF→(E)|i证明E+T*F是它的一个句型,指出这个句型的所有短语、直接短语和句柄。
《编译原理教程》课后习题答案第三章语法分析

第三章 语法分析 来消除左递归。由此,将产生式B→Bb|d改造为
B→dB′ B′→bB′| ε
其次,应通过提取公共左因子的方法来消除G[A]中的回 溯,即将产生式A→aABl|a改造为 A→aA′ A′→ABl | ε
最后得到改造后的文法为 G[A′]:A→aA′ A′→ABl | ε B→dB′ B′→bB′| ε
S→(T) | aS′ S′→+S | ε T→ST′ T′→,ST′| ε 改造后的文法已经是LL(1)文法,不带回溯的递归子程序如下: void match (token t)
{ if ( lookahead==t) lookahead=nexttoken; else error ( ); }
第三章 语法分析 void S ( ) {
第三章 语法分析 3.3 已知文法G[S]为S→aSb|Sb|b,试证明文法
G[S]为二义文法。 【 解 答】 由 文 法G[S] :S→aSb|Sb|b ,对 句 子
aabbbb可对应如图3-1所示的两棵语法树。
第三章 语法分析
S aSb aSb
Sb b
S Sb aSb aSb b
图3-1 句子aabbbb对应的两棵不同语法树
第三章 语法分析
求得:
FIRST(A)={a}
FIRST(A′)={a, ε }
FIRST(B)={d}
FIRST(B′)={b, ε }
对文法开始符号A,有FOLLOW(A)={#}。
由 A′→ABl 得 FIRST(B)\{ ε }FOLLOW(A) , 即 FOLLOW(A)={#,d};
第三章 语法分析 【解答】 (1) 消除左递归后,文法G[D′]如下:
D→TL T→int|long|short L→idL
编译原理(龙书)答案第三章

编译原理(龙书)答案第三章3.3.2, 3.3.6, 3.3.7, 3.3.8, 3.3.9,3.6.3, 3.6.4, 3.6.53.7.1, 3.7.2, 3.7.33.8.1, 3.8.23.9.3《编译原理》(龙书)第三章答案3.3.2 描述下列正则表达式代表的语⾔。
a) a(a|b)*ab) ((ε|a)b*)*c) (a|b)*a(a|b)(a|b)d) a*ba*ba*ba*e) (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*答案(a)由a开头并结尾的由a和b构成的字符串(b)由a和b构成的字符串(c)倒数第三位为a的由a和b构成的字符串(d)仅含3个b的由a和b构成的字符串(e)含有偶数个a和偶数个b的由a和b构成的字符串注意:请准确描述语⾔的性质⽽不是列举满⾜正则表达式的串3.3.6 写出满⾜下列定义的字符a) The first ten letters in either upper or lower caseb) The lowercase consonantsc) The “digits” in a hexadecimal numberd) The characters that can appear at the end of a legitimate English sentence 答案(a)a-jA-J(b)a-j(c)0-9a-f(d).?!3.3.7 写出匹配字符串“\ 的正则表达式答案:\”\\3.6.3 对于图3.29表⽰的NFA,列出aabb的所有路径。
这个NFA能否接受aabb? 答案:aabb的所有路径01223 00111 012000 00000 01222 00011 00123存在路径1223和0123所以能接受aabb3.6.4 对于图3.30表⽰的NFA,列出aabb的所有路径。
这个NFA能否接受aabb? 答案:01012301012120301230301212030303232030303212303030321212由于存在03210这样的环,所以这⾥有⽆数种路径存在路径终⽌于3,所以能接受aabb3.6.5 给出以下NFA的Transition Table(a) 图3.29(b) 图3.30(c) 图3.26答案:3.7.1 把下列NFA转化为DFA(a)图3.26(b)图3.29(c)图3.30答案:(a)(b)注意:以上答案并不唯⼀,等价即可3.7.2 ⽤算法3.22模拟NFA(输⼊为aabb)(a)图3.29(b)图3.30答案:F={3} 所以返回yesF={3},所以返回yes3.7.3 ⽤算法3.23和3.20把下列正则表达式转换为DFAa) (alb)*b) (a*lb* )*c) ((ela)b*)*d) (alb)*abb(alb)*答案:a) NFAb) NFAc) NFAd) NFA注意:这道题要求⼤家按照算法构造NFA和DFA,有些同学的NFA没有完全按照算法构造。
编译原理 第3章习题解答
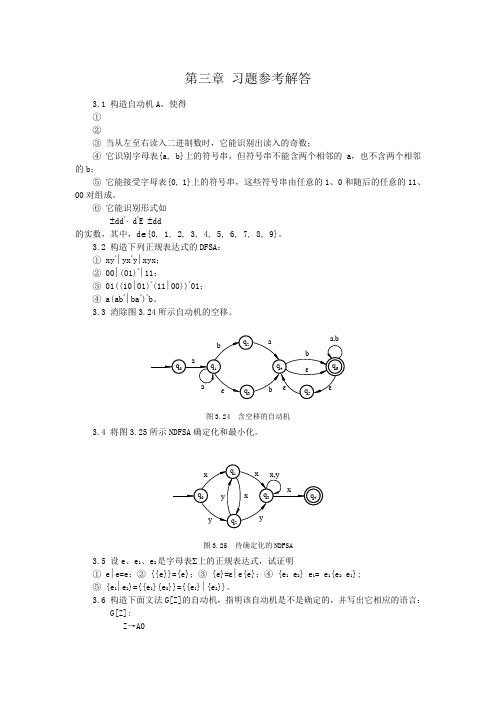
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA 确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉 〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉 〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉 〈字母〉→a ∣b 〈数字〉→1∣2试写出相应的有限自动机和状态图。
3.9 图3.29所示的是一个NDFSA A ,试构造一个正规文法G ,使得L(G)= L(A)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章文法和语言5. 写一文法,使其语言是偶正整数的集合要求:(1)允许0打头(2)不允许0打头解:(1)G[S]=({S,P,D,N},{0,1,2,…,9},P,S)P:S→PD|DP->NP|ND→0|2|4|6|8N->0|1|2|3|4|5|6|7|8|9(2)G[S]=({S,P,R,D,N,Q },{0,1,2,…,9},P,S)P:S→PD|P0|DP->NR|NR->QR|QD→2|4|6|8N->1|2|3|4|5|6|7|8|9Q->0|1|2|3|4|5|6|7|8|96. 已知文法G:<表达式>::=<项>|<表达式>+<项>|<表达式>-<项><项>::=<因子>|<项>*<因子>|<项>/<因子><因子>::=(<表达式>)|i。
试给出下述表达式的推导及语法树。
(1)i; (2)(i) (3)i*i;(4)i*i+i; (5)i+(i+i); (6)i+i*i。
解:(1)v=<表达式>=><项>=><因子>=>i=w(2)v=<表达式>=><项>=><因子>=>(<表达式>)=>(<项>)=>(<因子>)=>(i)=w(3)v=<表达式>=><项>=><项>*<因子>=><因子>*<因子>=>i*i=w(4)v=<表达式>=><表达式>+<项>=><项>+<项>=><项>*<因子>+<项>=><因子>*<因子>+<因子>=>i*i+i=w(5)v=<表达式>=><表达式>+<项>=><项>+<项>=><因子>+<因子>=>i+(<表达式>)=> i+(<表达式>+<项>)=>i+(<项>+<项>)=> i+(<因子>+<因子>)=>i+(i+i)=w(6)v=<表达式>=><表达式>+<项>=><项>+<项>=><因子>+<项>=>i+<项>=>i+<项>*<因子>=> i+<因子>*<因子>=> i+i*i=w语法树见下图:7. 为句子i+i*i 构造两棵语法树,从而证明下述文法G[<表达式>]是二义的。
<表达式>::=i|(<表达式>)|<表达式><运算符><表达式> <运算符>::=+|-|*|/解:为句子i+i*i 构造的两棵语法树如下:所以,该文法是二义的。
<表达式> <项> <因子> i<表达式> <项> <因子> ( <表达式> )<项> <因子> i<表达式> <项><项> * <因子><因子> ii<表达式><表达式> + <项> <项> <项> * <因子> <因子> ii<因子> i<表达式><表达式> + <项> <项> <因子> i<因子> ( <表达式> )<表达式> + <项> <项> <因子>i<因子> i<表达式><表达式> + <项> <项> <因子> i<项> * <因子> <因子> ii(1)i (2)(i) (3)i*i (4) i*i+i (5) i+(i+i) (6) i+i*i <表达式> <表达式> + <表达式> i <表达式> * <表达式> i i <表达式><表达式> * <表达式><表达式> + <表达式> i ii8. 习题1中的文法G[S]是二义的吗?为什么?答:是二义的。
因为对于句子abc 可以有两种不同的生成树,即:S=>Ac=>abc 和S=>aB=>abc 11. 令文法G[E]为: E →T|E+T|E-T T →F|T*F|T/F F →(E)|i证明E+T*F 是它的一个句型,指出这个句型的所有短语、直接短语和句柄。
解:可为E+T*F 构造一棵语法树(见下图),所以它是句型。
从语法树中容易看出,E+T*F 的短语有:T*F 是句型E+T*F 的相对于T 的短语,也是相对于规则T →T*F 的直接短语。
E+T*F 是句型E+T*F 的相对于E 的短语。
句型E+T*F 的句柄(最左直接短语)是T*F 。
12. 下述文法G[E]生成的语言是什么?给出该文法的一个句子,该句子至少含五个终结符,构造该句子的语法树。
证明:<E><T><F><MOP><POP>是G[<E>]的句型,并指出该句型的所有短语、直接短语和句柄。
<E>→<E><T><POP>|<T> <T>→<T><F><MOP>|<F> <F>→a|b|c <POP>→+|- <MOP>→*|/ 解:(1)计算文法G[E]的语言:由于L(T)={(a|b|c)((a|b|c)(*|/))n|n>=0}所以L(E)={L(T)(L(T)(+|-))n |n>=0}(2)该文法的一个句子是aab*+,它的语法树是:(3) 证明:<E><T><F><MOP><POP>是G[<E>]的句型,并指出该句型的所有短语、直接短语和句柄。
由于下面的语法树可以生成<E><T><F><MOP><POP>,所以它是G[<E>]的句型。
EE + TT * F<E><E> <T> <POP><T> <F> <MOP> <T> <F> a <F> ab *+<E><E> <T> <POP><T> <F> <MOP>由于<E> => <E><T><POP>,且<T> => <T><F><MOP>,所以<T><F><MOP>是句型<E><T><F><MOP><POP>相对于<T>的短语,也是相对于规则<T> → <T><F><MOP>的直接短语。
由于<E> => <E> 且<E> => <E><T><F><MOP><POP>,所以<E><T><F><MOP><POP>是句型<E><T><F><MOP><POP>相对于<E>的短语。
显然,句型<E><T><F><MOP><POP>的句柄是<T><F><MOP>。
14. 给出生成下述语言的上下文无关文法:(1){a n b n a m b m|n,m>=0}(2){1n0m1m0n|n,m>=0}(3){WaW t|W属于{0|a}*,W表示W t的逆}解:(1)所求文法为G[S]=({S,A},{a,b},P,S),其中P为:S→AAA→aAb|ε(2)所求文法为G[S]=({S,A},{0,1},P,S),其中P为:S→1S0|AA→0A1|ε(3)W属于{0|a}*是指W可以的取值为{ε,0,a,00,a0,aa0,00aa,a0a0,…}如果W=aa0a00,则W t=00a0aa。
所求文法为G[S]=({S,P,Q},{0,a},P,S),其中P为:S→0S0|aSa|a15. 语言{WaW}和{a n b m c n d m}是上下文无关的吗?能看出它们反映程序设计语言的什么特性吗?答:生成语言{WaW}的文法非常简单,如G[S]: S→WaWW→aW|bW|ε可见G[S]是上下文无关的。
生成语言{a n b m c n d m}的文法非常复杂,用上下文无关文法不可能办到,只能用上下文有关文法。
这是因为要在a n c n的中间插入b m而同时要在其后面插入d m。
即a,c相关联,b,d相关联。
这说明对语言的限定越多(特别是语言中的符号前后关联越多),生成它的文法越复杂,甚至于很难找到一个上下文法无关文法。
16.给出生成下述语言的三型文法:(1){a n|n>=0}(2){a n b m|n,m>=1}(3){a n b m c k|n,m,k>=0}解:(1)生成的3型文法是:G[S]:S→aS|ε(2)生成的2型文法是:G[S]: S→ABA→aA|aB→bB|b生成的3型文法是:G[S]:S→aPP→aP|bDD→bD|ε(3)生成的2型文法是:G[S]: S→ABCA→aA|εB→bB|εC->cC|ε生成的3型方法是:G[S]:A→aA|bB|cC|εB→bB|cC|εC→cC|ε。
