某配送中心向六家超市节约里程法
运输的优化求解、运输问题—节约里程法

1、列运输平衡表
列表时要求表内供销平衡,并将运费标入表内空格。
需
供
B1
B2
B3
A1
x11 90 x12 70 x13 100
供应量 200
A2
x21 80 x22 65 x23 80
250
需求量 100 150
200
250
需求量 100 150
200
450
由于上表中有负检验数,故需继续 进行调整,得新运输方案表。
新运输方案2表
需
供
B1
B2
B3
A1
100 90 100 70
100
A2
80 50 65 200 80
需求量 100
150
200
供应量 200 250 450
对新运输方案表进行检验。
新运输方案2检验表
其需量等于总供量与总需量之差,并设其相应运价为0。这
样,就可以用表上作业法求解产大于销的运输问题。
2、销大于产的运输问题 n m
对于销量大于产量,即 bj ai 的运输问题,必
j 1
i 1
然有一些销地不能得到满足,发生缺货,此时引入虚拟供
应点,并设其相应运价为0。这样,就可以用产销平衡的表
上作业法求解销大于产的运输问题。
450
2、建立初始调运方案
采用最小元素法,即在平衡表中挑取运价最小或
较小的供需点格子尽量优先分配的调运方法。
需
供
B1
A1
0 90
B2
B3
供应量
节约里程法的举例
7
P4
2.5
5
13
9
13
10
P5
1.6
15
22
18
22
19
9
P6
1.8
19
27
23
30
30
20
11
P7
解:(1)先优化配送路线,计算节约里程数。(本步骤计5分)
第一步。根据运输里程表,按节约里程公式,求出相应的节约里程数,如下表括号内数字示
需要量
P0
2.8
8
P1
1.7
4
5(7)
P2
0.8
11
9(10)
4(11)
P3
1.4
12
16(4)
11(5)
7(16)
P4
2.5
5
13(0)
9(0)
13(3)
10(7)
P5
1.6
15
22(1)
18(1)
22(4)
19(8)
9(11)
P6
1.8
19
27(0)
23(0)
30(0)
30(1)
20(4)
11(23)
P7
第二步,按节约里程数大小的顺序排序(本步骤计5分)
序号
⑵设配送中心在向用户配送货物过程中单位时间平均支出成本为45元,假定卡车行驶的平均速度为25公里/小时,试比较优化后的方案比单独向各用户分送可节约多少费用?
(3)、配送货物的运输量是多少?
(4)、配送货物的周转量是多少?
表1运输里程表
需要量
P0
2.8
8
P1
1.7
4
5
节约里程法应用案例

节约里程法应用案例在当今竞争激烈的商业环境中,物流成本的有效控制对于企业的生存和发展至关重要。
节约里程法作为一种优化配送路线的有效方法,能够显著降低运输成本,提高物流效率。
接下来,让我们通过一个具体的案例来深入了解节约里程法的实际应用。
假设我们有一家位于城市中心的配送中心,需要向位于城市不同区域的五个客户(A、B、C、D、E)配送货物。
每个客户的需求量以及他们之间的距离如下表所示:|客户|需求量(吨)|与配送中心距离(公里)||||||A|5|10||B|8|12||C|3|8||D|6|15||E|4|11||客户|A|B|C|D|E|||||||||A| | 18 | 22 | 25 | 16 ||B| 18 || 10 | 18 | 12 ||C| 22 | 10 || 14 | 9 ||D| 25 | 18 | 14 || 20 ||E| 16 | 12 | 9 | 20 ||首先,我们按照传统的方法,即每个客户单独配送,计算出总运输里程。
配送中心到客户 A 的往返里程为 2×10 = 20 公里。
配送中心到客户 B 的往返里程为 2×12 = 24 公里。
配送中心到客户 C 的往返里程为 2×8 = 16 公里。
配送中心到客户 D 的往返里程为 2×15 = 30 公里。
配送中心到客户 E 的往返里程为 2×11 = 22 公里。
总运输里程为 20 + 24 + 16 + 30 + 22 = 112 公里。
接下来,我们应用节约里程法来优化配送路线。
第一步,计算两两客户之间的节约里程数。
例如,客户 A 和客户 B 之间的节约里程数为:(配送中心到 A 的距离+配送中心到 B 的距离 A 到 B 的距离)× 2 =(10 + 12 18)× 2 = 8 公里。
按照同样的方法,计算出所有两两客户之间的节约里程数,如下表所示:|客户|A|B|C|D|E|||||||||A| | 8 | 6 | 5 | 2 ||B| 8 || 4 | 3 | 4 ||C| 6 | 4 || 2 | 3 ||D| 5 | 3 | 2 || 5 ||E| 2 | 4 | 3 | 5 ||第二步,根据节约里程数的大小对路线进行合并和优化。
[计算题]节约里程法答案讲解学习
![[计算题]节约里程法答案讲解学习](https://img.taocdn.com/s3/m/7d22229e80eb6294dd886c78.png)
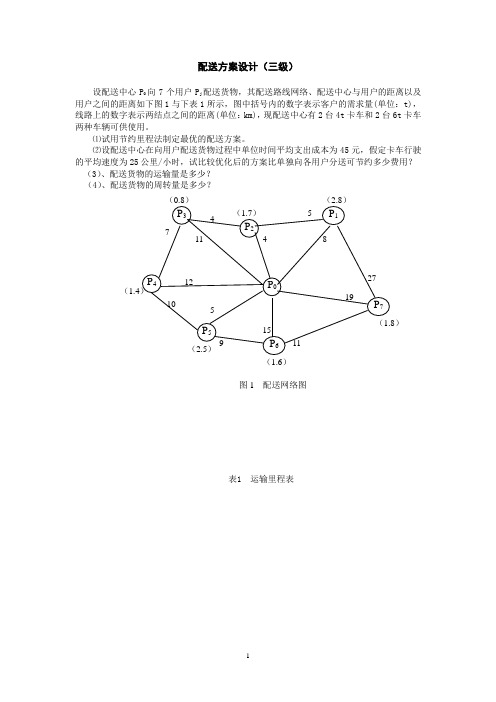
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
配送节约里程法讲义
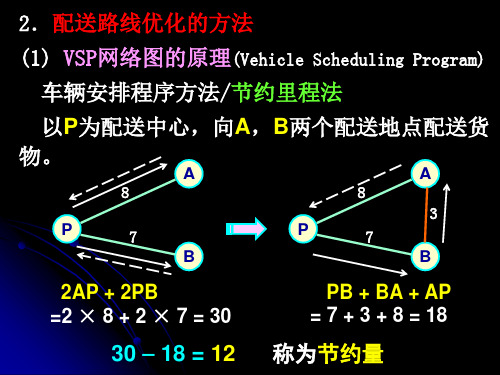
由节约里程数表可知: 由节约里程数表可知: EG节约里程最大 节约里程最大, ● EG节约里程最大,配送货物量是 1.75+1.15=2.9t,在货车载重限度内,可以入选。 1.75+1.15=2.9t,在货车载重限度内,可以入选。 ●FG的配送货物量1.1t,可与2.9t拼装为一辆4t FG的配送货物量1.1t,可与2.9t拼装为一辆4t 的配送货物量1.1t 2.9t拼装为一辆 货车的载运量; 货车的载运量; ●由此衔接成为一条配送路线AEGFA(AFGEA) ; 由此衔接成为一条配送路线AEGFA(AFGEA) AEGFA 全程为20+1+6+24=51 km。 ● 全程为20+1+6+24=51 km。 4t货车装满。 4t货车装满。 货车装满
要向所在城市B, , , , 例:某配送中心A要向所在城市 ,C,D,E, 配送中心 要向所在城市 F,G共6个客户点配送货物,它们之间的距离和 , 共 个客户点配送货物, 点配送货物 每一处的配送货物量见下表。运输车辆有2. 每一处的配送货物量见下表。运输车辆有 .5 t 两种货车。 和4 t两种货车。试确定配送路线。 两种货车 试确定配送路线。
最短距离表 A B C D E F G A 0 B 9 0 C 12 9 0 D 12 19 10 0 E 20 29 32 25 0 F 24 33 29 19 6 0 G 21 30 33 25 1 6 0
节约里程数表 序号 组合 节约里程 8 CF 7 1 EG 40 9 DE 7 2 FG 39 10 BD 2 3 EF 38 B E 0 4 DF 17 B F -5 CD 14 B G -6 BC 12 C E -7 DG 8 C G --
【管理资料】节约里程法例题计算汇编

顺序排位
1 2 3 4 4 6 6 6 9 9 11 12
连接线
A- B A- J B- C D- E C- D A- I E- F I- J A- C B- J B- D C- E
节约里程
15 13 11 10 10 9 9 9 8 8 7 6
顺序排位
13 13 13 16 16 16 19 19 21 22 22 22
C
D
B
A 0.32
0.24
路线1 2
E
P 路线2 2
J 0.24
F
G
路线3 2
0.16
0.48
H
0.40
图2 配送路线图
I 0.32
从配送路线图可看出,依次确定的三条配送路线均符合配送中心的约 束条件,需要2t货车3辆,总走行里程为70km,若简单地每个连锁分店 送货,需要2t货车10辆,走行总里程148km。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
连接线
F- G G- H H- I B- I A- D F- H B- E D- F G- I C- J E- G F- I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
第四步:根据节约里程排序表和配送车辆载重及行驶里程等约束 条件,渐近绘出如图2所示的配送路线图。
0.32
0.40
0.40
第二步:由最短距离表,利用“节约里程”法计算出各连锁分店之 间的节约里程,做出节约里程表(见表3),计算结果有正有负, 节约里程为负数时,无实际意义,在表内写0。
表3 节约里程表
A BC DE F GH I J A B C D E F G H I J
[计算题]节约里程法答案
![[计算题]节约里程法答案](https://img.taocdn.com/s3/m/a35e5204915f804d2b16c1cd.png)
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
物流线路规划节约里程法案例详解

节约里程法案例详解假如由一家配送中心P向两个用户A、B送货,配送中心到两客户的最短距离分别是L1和L2,A和B间的最短距离为L3,AB的货物需求量分别是Q1和Q2,且Q1+Q2小于车辆装载量Q【如果Q1+Q2大于车辆装载量Q,那一辆车就无法装完两位客户的货物】。
如下图所示:如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时,汽车行驶的总里程L是L=2(L1+ L2)如果用一辆汽车向A、B两个用户巡回送货,则汽车行驶总里程L′为L′= L1+ L2+L3根据三角形的一边之长必定小于另外两边之和的原理,后一种配送方案比前一种方案节约里程△L为△L=2(L1+ L2)-(L1+ L2+L3)= L1+ L2-L3【这就是节约里程法产生的初衷,以最短距离最优配载完成送货作业】案例:位于市内的百家姓配送中心(P0)向它旗下的10家连锁商店p i(i=1,2,…,10)配送商品,其配送网络如下图所示。
图中括号内的数字表示每一家连锁店的需求量(t),线路上的数字表示两节点之间的距离(km)。
配送中心现有2t和4t车辆可供使用(无数量限制),并且每辆车配送距离不得超过30km。
请为百家姓配送中心制定最优的配送方案。
分析:初始方案:如果从P点向各点分别派车送货。
1、从百家姓配送中心出发,需要设计10条配送线路,分别向10家连锁店配送商品;2、需要10辆2t的配送车辆(每家连锁店的需要量都低于2t),总配送距离为148km。
第二种:节约里程法解题思路:相互间的节约里程计算根据△L== L1+ L2-L3 原理,例如以“百家姓配送中心交通图”中的P0(配送中心)到客户d、客户c的节约里程为例:dc△L==P0d(L1)+P0c (L2)-dc(L3 )==8 + 7 - 5=10如此计算出客户d和客户c间的节约里程数为10,以此方法计算出各个节点的节约里程数。
方案修正过程(优化到最终线路)1、方案修正过程实际上是线路规划过程,根据节约里程法原理从节约里程数最大的节点开始选择(这是先要排序的原因);2、所有规划线路的起点和终点都是配送中心,这里是P0;3、最大节约里程是a和b间的节约里程数15,那么路线的走向可以是P0-A或P0-B。
