行测数量关系技巧:年龄问题的巧解方法
公务员行测《年龄问题解题技巧》

年龄问题解题技巧年龄问题是公务员考试行测中的一种常见题型,国家公务员考试网认为,解决这类问题首先要了解年龄的三大特点:(1)两个人年龄差不变(2)两个年龄的倍数关系是变化的量(随着年龄的增长,两个人的倍数关系会越来越小,无限接近于1倍)(3)每个人的年龄的增长量相同(过一年长一岁)。
年龄问题的常见解题方法:画时间轴,代入排除,方程,整除等等,下面我们通过几道真题给大家进行讲解例1.一位长寿老人出生于19世纪90年代,有一年他发现自己年龄的平方刚好等于当年的年份。
问这位老人出生于哪一年? ( )。
A.1894年B.1892年C.1898年D.1896年【答案】由题意可知,当他 44岁那年为1936年,所以1936-44=1892,因此答案为B。
【点评】在年龄问题中,大家需要记住两个平方数,,原因在于考试中会出现比如某一个人出生的年份是一个平方数这一类的条件,但出现这一类条件的时候我们基本就可以把数字锁定为1936,因为只有此数符合题意,比如43的平方为1849,不可能成立,而记住目的在于考试可能会出现家里的孩子过了多少年后,此时的年份是平方数,我们就可以锁定为2025,所以,大家一定要牢牢记住。
例2.有一位百岁老人出生于二十世纪,2015年他的年龄各数字之和正好是他在2012年的年龄的各数字之和的三分之一,问该老人出生的年份各数字之和是多少(出生当年算作0岁)。
A.14B.15C.16D.17【答案】生于二十世纪,所以2015年老人的年龄最大也不会超过2015-1900=115,因为2012年和2015年相差3年,而2012年他的年龄是3的倍数,那么,2015年他的年龄也一定是3的倍数,且年龄的个位数字小于3,所以2015年的年龄=111、出生年份=2015-111=1904,各位数字之和=1+9+0+4=14,选A。
【点评】此题涉及到了整除的思想,而且还需要根据实际情况进行数字之间关系的分析,所以,有的时候数量关系题,尤其是与我们生活实际的数量题目,除了要有一些数学思维之外,还需要我们能联系实际考虑问题,做题与猜题相结合,迅速做出答案。
2015年河北公务员考试行测答题技巧:年龄问题巧回答

2015年河北公务员考试行测答题技巧:年龄问题巧回答行测答题技巧:在公务员行测的数量关系部分,有一类问题叫年龄问题。
年龄问题的题型特征是题目中会出现一个或者多个人的年龄变化,求某个人的年龄。
这类年龄问题的解题核心是年龄差不变。
解题方法有三种:代入排除法,列表法和方程法。
下面通过几道题看看年龄问题的解法。
例1.小鲸鱼说:“妈妈,我到您现在这么大时,您就31岁啦!”大鲸鱼说:“我像你这么大年龄时,你只有1岁。
”请问小鲸鱼现在几岁?A.13B.12C.11D.10【答案】C。
解析:方法一:代入排除法。
代入A选项,如果小鲸鱼现在13岁,则大鲸鱼13岁,小鲸鱼只有1岁,年龄差是12岁,则大鲸鱼现在13+12=25岁,当小鲸鱼长到25岁时,大鲸鱼应该是25+12=37岁,不对;同理,代入C选项,如果小鲸鱼现在11岁,则大鲸鱼11岁,小鲸鱼只有1岁,年龄差是10岁,则大鲸鱼现在11+10=21岁,当小鲸鱼长到21岁时,大鲸鱼应该是21+10=31岁,正确。
选C。
方法二:列表法。
题目中有大小两只鲸鱼,有三个时间点,过去,现在,将来,故可以列下表:设大鲸鱼现在y岁,小鲸鱼现在x岁。
过去现在将来大鲸鱼xy31小鲸鱼1xy根据年龄差不变列方程:x-1=y-xy-x=31-y解得:x=11。
选C。
例2. 甲、乙、丙、丁四人,其中每三个人的岁数之和分别是55、58、62、65。
这四个人中年龄最小的是( )。
A.7岁B.10岁C.15岁D.18岁【答案】C。
解析:由题意可知,65岁肯定是年龄较大的三个人的年龄和,55肯定是年龄较小的三个人年龄和,而且把四个数加起来,正好相当于把每个人算了3次,因此四个人的岁数和为(55+58+62+65)÷3=80,那么年龄最小的为80-65=15岁。
选C。
例3. 在一个家庭里,现在所有成员的年龄加在一起是73岁。
家庭成员中有父亲、母亲、一个女儿和一个儿子,父亲比母亲大3岁,女儿比儿子大2岁。
行测技巧:学会举一反三,搞定年龄问题
行测技巧:学会举一反三,搞定年龄问题近年来省考行测数量关系题目不断推陈出新,出现了很多变相的年龄问题,多数考生仅仅掌握了基本的方程法来解决年龄问题,但是对于题干具体的条件梳理缺乏逻辑性,导致很多特殊的题型难以应对。
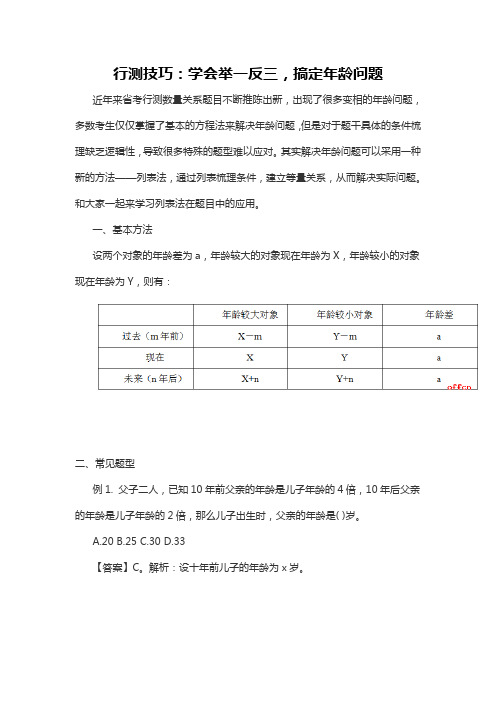
其实解决年龄问题可以采用一种新的方法——列表法,通过列表梳理条件,建立等量关系,从而解决实际问题。
和大家一起来学习列表法在题目中的应用。
一、基本方法设两个对象的年龄差为a,年龄较大的对象现在年龄为X,年龄较小的对象现在年龄为Y,则有:二、常见题型例1. 父子二人,已知10年前父亲的年龄是儿子年龄的4倍,10年后父亲的年龄是儿子年龄的2倍,那么儿子出生时,父亲的年龄是( )岁。
A.20B.25C.30D.33【答案】C。
解析:设十年前儿子的年龄为x岁。
根据题意,有4x+20=2(x+20),x=10,所以十年前儿子年龄为10岁,父亲年龄为40,所以儿子出生时,父亲年龄为30岁。
故答案为C。
例2. 今年甲乙丙三人年龄之和为83,甲今年25岁,当乙像甲现在这么大时,甲乙两人年龄之和比丙当时的年龄还大2岁。
问乙今年的年龄为多少岁?A.10B.12C.14D.15【答案】A。
解析:设今年乙的年龄为x岁,丙的年龄为y岁。
根据题干信息有:x+y+25=83,25+(25-x)+25=y+(25-x)+2,解得x=10,y=48,故答案为A。
例3. 现在父母年龄和是他们几个子女年龄和的6倍,两年前父母年龄和是他们几个子女年龄和的10倍,六年后父母年龄和是他们几个子女年龄和的3倍,那么他们有几个子女?A.2B.3C.4D.5【答案】B。
解析:设现在n个子女的年龄和为x,则现在父母的年龄和为6x。
根据题意有:6x-4=10(x-2n),6x+12=3(x+6n),解得x=14,n=3,故答案为B。
例4. 有80颗珠子,5年前,姐妹两人按年龄的比例分配,恰好分完;今年,她们再次按年龄的比例重新分配,又恰好分完。
行测数量关系技巧:弄懂年龄问题

行测数量关系技巧:弄懂年龄问题年龄是我们日常生活中熟知的一个概念,它经常也会出现在公考行测数量关系的题目中。
面对这样一个非常熟悉的概念,在考试过程中我们又能否把它快速求解出来呢?有些同学可能信心满满、跃跃欲试,小编就先带大家看一道题目感受一下:例1. 弟弟对哥哥说:“当我像你这么大的时候,你都23岁了!”哥哥则说:“我像你这么大的时候,你才11岁呢。
”请问弟弟现在的年龄是多少?A. 13B. 14C. 15D. 16看完这道题目,大家可能有点懵,他们之间的年龄到底有什么关系呢?哥哥和弟弟又到底多少岁呢?不要着急,这就为大家一一解答!首先,我们在做年龄问题时,要抓住一个基本关系——年龄差不变。
意思就是指两个对象的年龄差是一个恒定值,随着时间的推移,只要是在两个对象都存在的时间里,他们之间的年龄差值是一个固定的常数。
回到上面这道例题中,方法一:画图法方法二:列表法例2. 2007年父亲的年龄是30岁,儿子的年龄是3岁。
到多少年父亲的年龄是儿子年龄的4倍?A. 2010B. 2011C. 2012D. 2013【解析】答案:D。
父亲和儿子年龄差为27,如果父亲年龄是儿子年龄的4倍,父亲和儿子年龄差为儿子年龄的3倍,等于27,所以此时儿子年龄为9岁。
2007 年儿子是3岁,儿子长到9岁还需要六年时间,也就是2013 年。
故选D。
例3. 在一个家庭里,现在所有成员的年龄加在一起是73 岁。
家庭成员中有父亲、母亲、一个女儿和一个儿子,父亲比母亲大3 岁,女儿比儿子大2 岁。
四年前家庭所有人的年龄总和是58 岁,现在儿子多少岁?A. 3B. 4C. 5D. 6【解析】答案:A。
正常情况下,四年前每个人的年龄会少4岁,4名成员的年龄和总共会少16岁。
但实际上总和少了15岁。
说明家庭中最小的成员即儿子四年前还没有出生,少了一年,即现在儿子只有3岁。
故选A。
小结:当发现题目当中的年龄差出现数据矛盾时要能想到在某一年有成员还没有出生,差的年龄就是这样产生的,由相差的多少快速判断选项。
行测数量关系--还原与年龄问题之解答技巧

【典型问题】1. 某数加上6,乘以6,减去6,除以6,其结果等于6,则这个数是多少?解答:(6×6+6)÷6-6=1,这个数是1.2. 两个两位数相加,其中⼀个加数是73,另⼀个加数不知道,只知道另⼀个加数的⼗位数字增加5,个位数字增加1,那么求得的和的后两位数字是72,问另⼀个加数原来是多少?解答:和的后两位数字是72,说明另⼀个加数变成了99,所以原来的加数是99-51=48.3. 有砖26块,兄弟⼆⼈争着去挑。
弟弟抢在前⾯,刚摆好砖,哥哥赶到了。
哥哥看弟弟挑的太多,就抢过⼀半。
弟弟不肯,⼜从哥哥那⼉抢⾛⼀半。
哥哥不服,弟弟只好给哥哥5块,这时哥哥⽐弟弟多挑2块。
问最初弟弟准备挑多少块?解答:先算出最后各挑⼏块:(和差问题)哥哥是(26+2)÷2=14,弟弟是26-14=12,然后来还原:1. 哥哥还给弟弟5块:哥哥是14-5=9,弟弟是12+5=17;2. 弟弟把抢⾛的⼀半还给哥哥:抢⾛了⼀半,那么剩下的就是另⼀半,所以哥哥就应该是9+9=18,弟弟是17-9=8;3. 哥哥把抢⾛的⼀半还给弟弟:那么弟弟原来就是8+8=16块.4. 甲、⼄、丙三⼈钱数各不相同,甲最多,他拿出⼀些钱给⼄和丙,使⼄和丙的钱数都⽐原来增加了两倍,结果⼄的钱最多;接着⼄拿出⼀些钱给甲和丙,使甲和丙的钱数都⽐原来增加了两倍,结果丙的钱最多;最后丙拿出⼀些钱给甲和⼄,使甲和⼄的钱数都⽐原来增加了两倍,结果三⼈钱数⼀样多了。
如果他们三⼈共有81元,那么三⼈原来的钱分别是多少元?解答:三⼈最后⼀样多,所以都是81÷3=27元,然后我们开始还原:1. 甲和⼄把钱还给丙:每⼈增加2倍,就应该是原来的3倍,所以甲和⼄都是27÷3=9,丙是81-9-9=63;2. 甲和丙把钱还给⼄:甲9÷3=3,丙63÷3=21,⼄81-3-21=57;3. 最后是⼄和丙把钱还给甲:⼄57÷3=19,丙21÷3=7,甲81-19-7=55元.5. 甲、⼄、丙三⼈各有糖⾖若⼲粒,甲从⼄处取来⼀些,使⾃⼰的糖⾖增加了⼀倍;接着⼄从丙处取来⼀些,使⾃⼰的糖⾖也增加了⼀倍;丙再从甲处取来⼀些,也使⾃⼰的糖⾖增加了⼀倍。
2017黑龙江公务员考试行测技巧:巧解年龄问题.doc

2017黑龙江公务员考试行测技巧:巧解年龄问题
二、年龄问题的具体特点:
年龄问题重要特点为:①任何两个人年龄差不变;②任何两人年龄之间的倍数关系是变化的;③每过n年,所有的人都长了n岁。
三、年龄问题的巧解:
(一)时间轴法:画一条时间轴,年龄大的写在前,年龄小的写在后,设未知数表示年龄差,根据图形找等量关系。
【例题1】甲对乙说:当我的岁数是你现在的岁数时,你才5岁。
乙对甲说:当我的岁数是你现在的岁数时,你将50岁。
那么,甲现在几岁?
A.20
B.25
C.30
D.35
甲的年龄大于乙的年龄,故甲写在乙的右边,甲乙之间的年龄差设未知数x,甲像乙那么大时,乙5岁,故5和现在乙的年龄只差也是x,同理甲和50岁之前的差距也是x,由图可知,3x=45,x=15,故甲35岁,乙20岁。
(二)表格法:适用于多人、多年份的问题。
【例题2】爸爸、哥哥、妹妹现在的年龄和是64岁。
当爸爸的年龄是哥哥的3倍时,妹妹是9岁;当哥哥的年龄是妹妹的2倍时,爸爸34岁。
现在爸爸的年龄是多少岁?
A.34
B.39
C.40
D.42
【答案】D。
中公解析:题目是多人、多年份问题,直接找等量关系不好找,我们就可以列一个表格,把已知量在表格中表示出来,未知的量设未知数,然后根据年龄差不变去找等量关系。
更多黑龙江公务员考试报名入口相关信息请查看》》黑龙江公务员考试网。
2020国考行测数量关系:教你学会求解行测年龄问题

2020国考行测数量关系:教你学会求解行测年龄问题年龄问题在近几年的考试中频频出现在大家的视线里,而这一部分的知识对于大部分的考生来说也是可望而不可即,难度不小。
我们所讲,难者不会,会者不难,这一类题目在做题的过程中,是有一定的规律的。
因此呢,我们只需要掌握这一考点的解题原则和一些常见的考察形式就能够在考场中将这一类型题目的分数拿到手。
那么,接下来,中公教育就带大家来看看年龄问题中涉及到的一些知识点和解题思路。
一、基础知识年龄问题是指研究两人或者多人之间的年龄变化和关系的问题。
行测考试中常常涉及两人或者多人年龄之间的倍数关系。
二、解题原则1.任何两人年龄差不变;2.任何两人年龄之间的倍数关系是变化的,而且递减;3.每过一年,所有的人都长了一岁。
三、常见考点年龄问题的常见考察形式有以下几种:1.不同时刻年龄对比例1.小鲸鱼说:“妈妈,我到您这么大的时候,您就31岁了”,大鲸鱼说:“我像你这么大时候,你才1岁”。
问:小鲸鱼现在多少岁?【答案】11。
中公解析:根据解题原则,我们知道年龄差不变,假设大鲸鱼和小鲸鱼的年龄差为图中线段的长度,根据大小鲸鱼的描述,可以画出如上图所示的年龄轴,根据已知条件起点处年龄为1岁,终点处年龄为31岁,共差30岁,由3个年龄差组成,所以一个年龄差为10岁,现在小鲸鱼的年龄为11岁。
2.多人年龄问题例2.父亲与两个儿子的年龄和为84岁,12年后父亲的年龄等于两个儿子的年龄之和,请问父亲现在多少岁?A.24B.36C.48D.60【答案】C。
中公解析: 12年后,父亲与两个儿子的年龄和应该是84+12×3=120岁,将父亲12年后的年龄看做1倍,那么12年后父亲的年龄为120÷2=60岁,现在的年龄为60-12=48岁。
四、题目巩固例.2007年父亲年龄30岁,儿子3岁,到()年父亲年龄是儿子的3倍。
A.2012B.2013C.2014D. 2015【答案】B。
2022年公务员行测数量关系中年龄问题

2022年公务员行测数量关系中年龄问题行测全部是选择题,如果你找到了适合自己的答题速度和准确率的黄金结合点,你就离上岸不远了!想拿高分要学会放弃,更要掌握技巧,全力争取。
下面小编给大家带来关于公务员行测数量关系中年龄问题,希望会对大家的工作与学习有所帮助。
公务员行测数量关系中年龄问题一、年龄问题解题原则:1)年龄差不变;2)每个人都是自然增长;3)任何两人年龄之间的倍数关系是变化的。
我们通过例题来讲解一下:例1、在一个家庭中有爸爸、妈妈、女儿和儿子。
现在把所有成员的年龄加在一起是77岁,爸爸比妈妈大3岁,女儿比儿子大2岁。
5年前,全家所有人的年龄总和是58岁。
现在爸爸的年龄是多少岁?A.67B.32C.35D.78答案:C【解析】:根据题意“爸爸、妈妈、女儿和儿子。
现在把所有成员的年龄加在一起是77岁”,可得到5年前全家所有人的年龄和是58岁,由每个人都是增长,可知现在全家人的年龄总和应该是58+4×5=78岁。
但实际上的年龄总和却是77岁,差了1岁。
就说明有一个人只长了4岁,这个人只能是儿子因为5年前尚未出生。
女儿就应该是4+2=6岁,现在父母的年龄和是77-4-6=67岁,根据题意又已知知他们的年龄差是3岁,可求出爸爸的年龄是(67+3)÷2=35岁。
因此选择C选项。
例2、1998年,小张的年龄是小王的年龄的4倍。
2002年,小张的年龄是小王的年龄的3倍。
问小张、小王二人2000年的年龄分别是多少岁?A.34岁,12岁B.32岁,8岁C.36岁,12岁D.34岁,10岁答案:D【解析】:设1998年小王的年龄是x岁,则小张的年龄是4x岁。
从98年到02这四年4年,两个年龄都增长4岁,那么这个时候,小张的年龄是4x+4岁,小王的年龄为x+4岁。
由小张的年龄是小王年龄的3倍,因此有4x+4=3(x+4)可求得x=8。
也就是说1998年,小王的年龄是8岁,则2000年的年龄是10岁,因此选择D 选项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行测数量关系技巧:年龄问题的巧解方法
公务员行测考试主要是考量大家的数学推理能力和逻辑分析能力,下面由小编为你精心准备了“行测数量关系技巧:年龄问题的巧解方法”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:年龄问题的巧解方法
在行测考试中,年龄问题都我们考查的一个重点考题型,但此类题型难度并不大,总共涉及三个知识点和两种解题方法,理应是每位考生必须“拿下”的考题。
小编专家在此进行全面讲解:
一、年龄问题的主要的题型特点
①任何两人年龄差不变;②任何两人年龄之间的倍数关系是变化的;③每过一年,所有的人都长了一岁。
具体分类如下:
1.随时间推移,年龄差不变;
2.随时间推理,年龄倍数在减少;
3.过N年,长N岁。
二、如何巧解年龄问题
解决年龄问题的关键在于“年龄差不变”。
一般说来,解决年龄问题需要从表示年龄间关系的条件入手理解数量关系
例1:今年小宁8岁,妈妈32岁,那么再过多少年妈妈的岁数是小宁的2倍?
下面就为考生讲解如何巧妙解答年龄问题。
由差倍问题公式可得,小宁年龄为24÷(2-1)=24岁,即小宁24岁时,妈妈的年龄等于小宁的2倍,因此再过24-8=16年。
三、多人之间的年龄问题
多人之间的年龄问题在行测考试中出现的频率略有增加,它主要考查多个人之间的年龄关系变化。
解决此类题目的重点为规律③:每过一年,所有的人都长了一岁。
例题2:父亲与两个儿子的年龄和为84岁,12年后父亲的年龄等于两个儿子的年龄之和,请问父亲现在多少岁?
A.24
B.36
C.48
D.60
解析:此题答案为C。
12年后,父亲与两个儿子的年龄和应该是84+12×3=120岁,将父亲12年后的年龄看做1倍,那么12年后父亲的年龄为120÷2=60岁,现在的年龄为60-12=48岁。
四、年龄推理题
年龄推理题在行测考试中出现较少,它需要考生通过寻求年龄间的特殊情况来得到突破口,从而最终得出答案。
常见的特殊情况为:经过了N年,所有人增长的岁数和不是N的倍数,这说明N年前有人没有出生,从而可直接求出该人的年龄。
例题3:小芬家由小芬和她的父母组成,小芬的父亲比母亲大4岁,今年全家年龄的和是72岁,10年前这一家全家年龄的和是44岁。
今年父亲多少岁?
A.33
B.34
C.35
D.36
解析:此题答案为B。
一家人的年龄和今年与10年前比较增加了72-44=28岁,而如果按照三人计算10年后应增加10×3=30岁,只能是小芬少了2岁,即小芬8年前出生,今年是8岁,今年父亲是(72-8+4)÷2=34岁。
希望通过解读,让你对这个知识点有更好的的掌握,对于一般年龄问题,考生要把握住年龄差不变,过了N年都长N岁,但是对于新出生的和去世的情况要注意。
对于混合年龄问题可以通过十字交叉法进行计算。
