高一数学轮函数与方程训练题
高一数学函数与方程试题

高一数学函数与方程试题1.已知一元二次方程的两个实根为,且,则的取值范围是()A.B.C.D.【答案】A【解析】由程的二次项系数为1>0,故函数图象开口方向朝上又∵方程的两根满足0<x1<1<x2,则,即,即其对应的平面区域如下图阴影示:∵表示阴影区域上一点与原点边线的斜率,由图可知∈故选A.【考点】一元二次方程的根的分布与系数的关系;线性规划.2.函数的图象与轴的交点个数是()A.4B.3C.1D.0【答案】B.【解析】首先将函数化简为,然后根据函数与方程的关系知,要求“函数的图像与轴的交点的个数”就转化为求“方程的实数根的个数”,于是对其进行分类讨论:①当时,令,解得,,此时方程有两个实数根满足题意;②当时,令,解得,,因为,不满足,故舍去,所以此时方程有且仅有一个实数根满足题意. 综上所述,方程的实数根的个数有3个,即函数的图像与轴的交点的个数有3个,故选B.【考点】函数与方程.3.一艘船上午在A处,测得灯塔S在它的北偏东300处,且与它相距海里,之后它继续沿正北方向匀速航行,上午到达B处,此时又测得灯塔S在它的北偏东750,此船的航速是()海里/小时。
A.B.C.D.【答案】D【解析】由题意得在三角形中,,由正弦定理得,即,得,因此航行的速度.【考点】正弦定理在三角形中的应用.4.函数的零点个数为.【答案】【解析】函数的零点,就是方程的根,转化为与的图象交点的横坐标,结合图象知有两个交点,故零点个为2个.【考点】函数的零点,数形结合的数学思想.5.方程的解所在的区间是()A.B.C.D.【答案】C【解析】设,则由指数函数与一次函数的性质可知,函数与的上都是递增函数,所以在上单调递增,故函数最多有一个零点,而,,根据零点存在定理可知,有一个零点,且该零点处在区间内,故选答案C.【考点】函数与方程.6.二次函数中,,则函数的零点个数是()A.0个B.1个C.2个D.无法确定【答案】C【解析】令=0,二次函数的零点就是相应一元二次方程的根。
新高考数学一轮二轮复习专题-专题二 二次函数、方程与不等式(原卷版)-4月5月真题汇编

专题二 二次函数、方程与不等式一、单选题1.(2020·江苏省通州高级中学高一月考)不等式210ax ax ++>对于任意的x ∈R 恒成立,则实数a 的取值范围是( ) A .()0,4 B .[]0,4C .[)0,4D .(](),04,-∞⋃+∞2.(2021·山西高三一模(理))已知,,+∈a b c R ,且4,4a ab ac >+=,则2232a b c a b c+++++的最小值是( ) A .8B .6C .4D .23.(2021·安徽省泗县第一中学高二月考(文))已知0x >,0y >,211x y+=,若222x y m m +>-恒成立,则实数m 的取值范围是( )A .4m ≥或2m ≤-B .2m ≥或4m ≤-C .24m -<<D .42m -<<4.(2020·河北石家庄市·石家庄一中高一月考)命题:{|19}p x x x ∃∈≤≤,2360x ax -+≤,若p 是真命题,则实数a 的取值范围为( )A .37a ≥B .13a ≥C .12a ≥D .13a ≤5.(2020·河北石家庄市·石家庄一中高一月考)已知0,0,236x y x y >>+=,则xy 的值可能为( ) A .0B .1C .2D .36.(2021·浙江高三专题练习)已知[]1,1a ∈-时,不等式()24420x a x a +-+->恒成立,则x 的取值范围为( ) A .(-∞,2)∪(3,+∞) B .(-∞,1)∪(2,+∞) C .(-∞,1)∪(3,+∞)D .(1,3)7.(2021·全国高二单元测试)设x y z >>,n N ∈,且11nx y y z x z+≥---恒成立,则n 的最大值为( )A .2B .3C .4D .58.(2021·安徽高三月考(理))不定方程的整数解问题是数论中一个古老的分支,其内容极为丰富,西方最早研究不定方程的人是希腊数学家丢番图.请研究下面一道不定方程整数解的问题:已知()202022,x y y x Z y Z +=∈∈,则该方程的整数解有( )组. A .1B .2C .3D .49.(2020·河南高二月考(文))函数2y = )A .2B .4C .6D .810.(2021·全国高三专题练习(理))已知正数,a b 是关于x 的方程()2240x m x m -++=的两根,则11a b+的最小值为( ) A .2 B.C .4D.二、多选题11.(2020·江苏省包场高级中学高二月考)下列说法正确的是( ) A .1x x+的最小值为2 B .21x +的最小值为1 C .()32x x -的最大值为2D .2272x x ++最小值为2 12.(2020·河北石家庄市·石家庄一中高一月考)已知a ,b ,c ,d ∈R ,则下列命题为假命题的是( )A .若,a b c d >>,则ac bd >B .若a b >,则22ac bc ≥C .若0a b >>,则()0a b c ->D .若a b >,则a c b c ->-13.(2021·河北张家口市·高三一模)已知0,0a b >>,且281a b +=,则( ) A.433a b ->B1b C .22log log 6a b +-D .221168a b +<14.(2021·江苏南通市·海门市第一中学高二期末)若0a b >>,则( ) A .11a b b a+>+ B .11a b b b a a+<<+ C .114a b a b +≥+ D .144b a a ab ++的最小值为2 第II 卷(非选择题)请点击修改第II 卷的文字说明 三、填空题15.(2021·全国高三专题练习)已知1a >,b R ∈,当0x >时,[]24(1)1()02x a x b x---⋅-≥恒成立,则3b a +的最小值是_____. 16.(2021·天津高三一模)设0a >,0b >,且251ab b +=,则+a b 的最小值为___________.17.(2020·江苏常州市·常州高级中学高一期中)已知函数()21,1,23,1,x x f x x x ⎧+≤=⎨-+>⎩,若()2f a =,则实数a 所有可能的取值组成的集合为______.18.(2021·射阳县第二中学高二开学考试)若命题x R ∃∈,2410mx mx ++≤为假命题,则实数m 的取值范围是__________.19.(2021·江苏苏州市·苏州中学高二月考)已知正数a ,b 满足30a b ab +-+=,则ab 的最小值是________.20.(2021·浙江宁波市·高三月考)若正数,a b 满足2a b ab ++=,则3711a b +--的最小值是________.21.(2020·河北石家庄市·石家庄一中高一月考)已知1,0x y ,且1211x y+=-,则2x y +的最小值为________.22.(2021·江苏高三专题练习)设,a b 为正实数,且11410a b a b+++=,则4a b +的最大值与最小值之差为_______.23.(2020·上海高一专题练习)对于11a -≤≤,不等式()2210x a x a +-+->恒成立的x 的取值范围是_____________ 24.(2020·上海高一专题练习)若1,(0,0,,a bx y a b x y+=>>为正常数且a b ,则实数x y +的取值范围_________.25.(2021·吴县中学高一月考)已知110,0,121a b a b b >>+=++,则+a b 的最小值为________.26.(2021·苏州市第五中学校高一月考)正实数x ,y 满足:21x y +=,则当21x y+取最小值时,x =___________.27.(2021·浙江衢州市·高一月考)已知0a >,0b >且25a b +=,则21ab a b++的最小值为___________.28.(2021·浙江高三月考)设实数a ,b 满足0a >,1a b +=,则22212a b a b ++-的最大值是________.29.(2021·安徽滁州市·高一期末)已知0,0,4a b a b >>+=,则411a b ++的最小值为__________.四、解答题30.(2021·安徽高三二模(文))已知a ,b ,c 为正数,且满足3a b c ++=. (1)证明:1113ab bc ac++≥. (23≥.31.(2021·吉林吉林市·高二三模(文))已知函数()41,f x x x x R =-+-∈ (1)解不等式:()5f x ≤(2)记()f x 的最小值为M ,若正实数,a b 满足a b M +=,试求:1121a b +++的最小值32.(2020·江苏常州市·常州高级中学高一期中)已知0x >,0y >,4xy x y a =++. (1)当12a =时,求xy 的最小值; (2)当0a =时,求41x y x y+++的最小值. 33.(2020·泰州市第二中学高一期中)设函数2(),,,f x ax bx c a b c R =++∈.(1)若1a =,且关于x 的不等式()0f x <的解集是()1,2,解不等式210bx cx ++>; (2)若0,1,1a b a c <=-=-,解关于x 的不等式()0f x >;(3)若0,()a f x >在区间[1,0]-上的最大值是c ,且(1)(3)f f ≤-,求22453||ab a u a-=-的取值范围. 34.(2020·泰州市第二中学高一期中)(1)已知正数a b 、满足121a b+=,求ab 的最小值;(2)已知1x <,求函数1()1f x x x =+-的最大值. 35.(2020·江苏省通州高级中学高一月考)已知(),0a b ∈+∞,,1a b +=,求12y a b=+的最小值. 解法如下:()1212233b ay a b a b a b a b⎛⎫=+=++=++≥+ ⎪⎝⎭, 当且仅当2b a a b =,即1a =,2b =- 则12y a b=+的最小值为3+.应用上述解法,求解下列问题:(1)已知(),,0,a b c ∈+∞,1a b c ++=,求111y a b c=++的最小值; (2)已知10,2⎛⎫∈ ⎪⎝⎭x ,求1812y x x=+-的最小值; (3)已知正数123,,,,n a a a a ,满足1231n a a a a ++++=.求证:2222312122334112n n a a a a a a a a a a a a ++++≥++++. 36.(2020·上海高一专题练习)已知关于x 的一元二次方程x 2-(2k -1)x +k 2+k -1=0有实数根.(1)求k 的取值范围;(2)若此方程的两个实数根x 1,x 2满足2212x x +=11,求k 的值.37.(2020·泰州市第二中学高二月考)关于x 的不等式ax 2-(a +1)x +1<0 (1)若a=-2解关于x 的不等式ax 2-(a +1)x +1<0(2)若a >0解关于x 的不等式ax 2-(a +1)x +1<038.(2021·浙江高二期末)设函数2()f x x ax b =-+.(1)若不等式()0f x <的解集是{23}xx <<∣,求不等式210bx ax -+<的解集; (2)当3b a =-时,()0f x ≥恒成立,求实数a 的取值范围.39.(2021·全国高三专题练习)已知函数f (x )=x 2-2ax +5(a >1).若f (x )在区间(-∞,2]上是减函数,且对任意的x 1,x 2∈[1,a +1],总有|f (x 1)-f (x 2)|≤4,求实数a 的取值范围.40.(2021·安徽芜湖市·高一期末)在“基本不等式”应用探究课中,甲和乙探讨了下面两个问题:(1)已知正数x 、y 满足21x y +=,求12x y+的最小值.甲给出的解法是:由21x y +=≥,则128x y +≥=≥,所以12x y +的最小值为8.而乙却说这是错的.请你指出其中的问题,并给出正确解法;(2)结合上述问题(1)的结构形式,试求函数()1310122f x x x x ⎛⎫=+<< ⎪-⎝⎭的最小值.41.(2020·上海高一专题练习)求下列函数的最小值(1)21(0)x x y x x++=>;(2)2)y x R =∈;(3)226(1)1x x y x x ++=>-.42.(2020·上海高一专题练习)已知a >0,b >0,且a +b =1(1)求证:11(1)(1)9ab ++≥;(2)求证:4418a b +≥;(3)求证 (a +1a )(b +1b )≥254. 43.(2021·山东日照市·高一期末)已知函数2()21f x kx kx =+-.(1)若不等式()0f x <的解集为3,12⎛⎫- ⎪⎝⎭,求实数k 的值;(2)若方程()0f x =在[]12,有解,求实数k 的取值范围. 44.(2020·河南高二月考(文))已知关于x 的不等式222ax x ax -+<. (1)当1a =时,解不等式222ax x ax -+<; (2)当0a ≠时,解等式222ax x ax -+≥. 五、双空题45.(2021·渝中区·重庆巴蜀中学高一期末)已知a ,b R +∈,且2284a b +=,则2+a b的最大值为______;4122a b ++的最小值为______.。
2024年新高考版数学专题1_3.5 函数与方程及函数的综合应用(分层集训)

B.3
答案 B
C.4
D.5
)
3.(2022南京师范大学附中期中,7)用二分法研究函数f(x)=x3+2x-1的零点
时,第一次计算,得f(0)<0,f(0.5)>0,第二次应计算f(x1),则x1等于 (
A.1
B.-1
答案 C
C.0.25
D.0.75
)
4.(多选)(2022湖南师大附中三模,11)已知函数f(x)的定义域为R,且f(x)=f(x
1.(2023届长春六中月考,7)若函数f(x)=ln x+x2+a-1在区间(1,e)内有零点,则
实数a的取值范围是 (
A.(-e2,0)
C.(1,e)
答案 A
B.(-e2,1)
D.(1,e2)
)
2.(2017课标Ⅲ,文12,理11,5分)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,
A型
0.4
3
B型
0.3
4
C型
0.5
3
D型
0.4
4
则保温效果最好的双层玻璃的型号是 (
A.A型
答案 D
B.B型
C.C型
D.D型
)
3.(2020课标Ⅲ理,4,5分)Logistic模型是常用数学模型之一,可应用于流行
病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数
I(t)(t的单位:天)的Logistic模型:I(t)=
1 e
K
0.23( t 53)
,其中K为最大确诊病例数.
当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3) (
高一数学竞赛:函数与方程

高一数学竞赛:函数与方程模块一:易错试题精选【例1】若,a b c <<则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间()A (),a b 和(),b c 内()B (),a -∞和(),a b 内()C (),b c 和(),c +∞内()D (),a -∞和(),c +∞内【例2】若函数()⎩⎨⎧>≤+=0,ln 0,1x x x x x f ,函数()1y f f x ⎡⎤=+⎣⎦的零点个数是___________.【例3】已知函数()x f 是定义在R 上的奇函数,且当()+∞∈,0x 时,()x x f x2017log 2017+=,则函数()x f 的零点个数是A .1B .2C .3D .4【例4】奇函数f (x )、偶函数g (x )的图象分别如图1、2所示,方程f (g (x ))=0、g (f (x ))=0的实根个数分别为a 、b ,则a +b 等于()A.14B.10C.7D.3【例5】设函数11,(,2)()1(2),[2,)2x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩,则函数()()1F x xf x =-的零点的个数为A .4B .5C .6D .7【例6】函数322,2()log (2),2x x f x x x ⎧-≤⎪=⎨->⎪⎩,若函数()2–41()g x a f x x =-++有6个不同的零点,则a 的取值范围为()A.()0,2 B.(]0,2 C.(]0,1 D.()0,1【例7】设函数()4310{log 0x x f x x x +≤=>,,,若关于x 的方程()()()2230f x a f x -++=恰好有六个不同的实数解,则实数a 的取值范围为()A.()22-B.322⎛⎤- ⎥⎝⎦, C.3,2⎡⎫+∞⎪⎢⎣⎭D.()2,-+∞【例8】已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x m =有四个不同的解a b c d ,,,,且a b c d <<<,则的()21a b c c d++取值范围为()A.(]1,1- B.[)1,1- C.(1,)-+∞ D.(,1)-∞【例9】已知定义在R 上的函数()f x 满足(4044)4()f x f x -=-,若函数220192022x y x +=-与()y f x =的图象有m 个交点(,)(1,2,3)i i x y i m =L ,则1()miii x y =+=∑()(注111221()()()()mim m i x y xy x y x y =+=++++++∑L )A.2022mB.2019mC.2021mD.2024m模块二:培优试题精选【例1】已知定义在R 上的函数()f x 满足()()2f x f x +=,当[]1,1x ∈-时,()2f x x =,函数()()log 1,12,1a x x x g x x ⎧->=⎨≤⎩,若函数()()()h x f x g x =-在区间[]5,5-上恰有8个零点,则a 的取值范围为()A .(2,4)B .(2,5)C .(1,5)D .(1,4)【例2】关于x 的方程()242200x m x m ++++=有两个正根()1212,x x x x <,下列结论错误的是()A .102x <<B .226x <<C .1212x x x x +的取值范围是{01}xx <<∣D .2212x x +的取值范围是{440}xx <<∣【例3】设函数21,0()ln ,0ax ax x f x x x ⎧++≤⎪=⎨>⎪⎩,若函数()y f x a =+在R 上有4个不同的零点,则实数a 的取值范围是()A .4,3⎛⎫-+∞ ⎪⎝⎭B .(),0∞-C .[)1,0-D .4,13⎛⎤-- ⎥⎝⎦【例4】已知函数()()()2,0,2ln ,0,x x f x g x x x x x ⎧==-⎨>⎩,若方程()()()0f g x g x m +-=的所有实根之和为4,则实数m 的取值范围是()A .1m >B .1mC .1m <D .1m【例5】已知函数()2,1,121,11,,1,1xx x f x x x x x x ⎧<-⎪+⎪=--≤≤⎨⎪⎪>-⎩方程()()()()2220f x a f x a a R -++=∈的不等实根个数不可能是()A .2个B .3个C .4个D .6个【例6】已知函数()f x 是定义在R 上的奇函数,当0x >时,()()211,0212,22x x f x f x x ⎧--<≤⎪=⎨->⎪⎩,则函数()()1g x xf x =-在[)6,-+∞上的所有零点之和为()A .8B .32C .0D .18【例7】已知函数23e ,0()2,0x x x f x x x x ⎧-≤=⎨->⎩,()()2g x f x kx x =--有两个零点,则k 的可能取值为()A .2-B .1-C .0D .1【例8】设函数()f x 定义域为R ,(1)f x -为奇函数,(1)f x +为偶函数,当(1,1]x ∈-时,2()1f x x =-+,则下列结论正确的是()A .7324f ⎛⎫=-⎪⎝⎭B .(7)f x +为奇函数C .()f x 在(6,8)上为减函数D .方程()lg 0f x x +=仅有6个实数解【例9】已知函数()()211x xf x x x =->-,()()2log 11x g x x x x =->-的零点分别为α,β,给出以下结论正确的是()A .αββα=+B .22log ααββ+=+C .4αβ+>D .1αβ->-【例10】设()()ln ,024,24x x f x f x x ⎧<≤⎪=⎨-<<⎪⎩,若方程()f x m =有四个不相等的实根()1,2,3,4i x i =,则()2221234x x x x +++的取值范围为___________.【例11】设a ∈R ,对任意实数x ,记(){}2min 2,35f x x x ax a =--+-.若()f x 至少有3个零点,则实数a 的取值范围为______.【例12】已知偶函数()f x 满足()()33f x f x +=-,且当[0,3]x ∈时,()221f x x x =-++,若关于x 的方程()()230f x tf x --=在[150,150]-上有300个解,则实数t 的取值范围是_____.【例13】已知函数()f x 定义城为(]0,12,恒有(4)4()f x f x +=,(]0,4x ∈时2()22x f x -=-;若函数2()()()g x f x t f x =+⋅有4个零点,则t 的取值范围为________.【例14】已知函数212,2()2ln(1),2x x x f x x x ⎧-+<≤⎪=⎨⎪->⎩,当1,2x ⎛⎫∈+∞ ⎪⎝⎭时,函数1()()4g x f f x m ⎛⎫=+- ⎝⎭有6个不同的零点,求m 的取值范围___________.【例15】已知函数2|2|,0,()|log |,0,x x f x x x +≤⎧=⎨>⎩若关于x 的方程()0f x k -=有4个不相等的实数根a ,b ,c ,d ,则+++a b c d 的取值范围是___________,abcd 的取值范围是___________.【例16】已知函数()1ln ,1121,1x f x x x x ⎧⎛⎫-<-⎪ ⎪=+⎝⎭⎨⎪+-⎩,则函数()f x 的零点是__________;若函数()()()g x f f x a =-,且函数()g x 有三个不同的零点,则实数a 的取值范围是__________.【例17】已知函数()22,01ln ,0x x x f x x x ⎧--≤⎪=⎨+>⎪⎩,若存在互不相等的实数a ,b ,c ,d 使得()()()()f f b f d m a c f ====,则(1)实数m 的取值范围为_________;(2)+++a b c d 的取值范围是_________.【例18】已知函数()()2ln ,068,0x x f x x x x ⎧-<⎪=⎨-+≥⎪⎩,则函数()f x 的各个零点之和为______;若方程1f x mx ⎛⎫+= ⎪⎝⎭恰有四个实根,则实数m 的取值范围为______.模块三:全国高中数学联赛试题精选【例1】(全国竞赛题)已知定义在+R 上的函数)(x f 为⎩⎨⎧--=x x x f 41log )(39,90,>≤<x x ,设c b a ,,是三个互不相同的实数,满足)()()(c f b f a f ==,求abc 的取值范围。
2021届高三数学(文理通用)一轮复习题型专题训练:函数与方程(二)(含解析)

《函数与方程》(二)考查内容:主要涉及函数零点个数的判断(方程法、数形结合法、图象法、零点存在定理与函数性质结合法)一.选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数26,0()3ln ,0x x x f x x x ⎧--≤=⎨-+>⎩的零点个数为( )A .3B .2C .1D .02.已知函数ln ,0()2(2),0x x f x x x x ⎧>=⎨-+≤⎩,则函数()3y f x =-的零点个数是( )A .1B .2C .3D .43.函数()ln 1f x x x =-+的零点个数为( ) A .0B .1C .2D .34.已知函数()()y f x x R =∈满足(2)()f x f x +=,且(1,1]x ∈-时,2()f x x =,则4()log ||y f x x =-的零点个数为( ) A .8B .6C .4D .25.函数()sin 1f x x x =-在,22ππ⎛⎫- ⎪⎝⎭上的零点个数为( )A .2B .3C .4D .56.函数()22lg 2||f x x x x =+-的零点的个数为( ) A .2B .3C .4D .67.已知函数23(0),()1(0),x x x x f x e x -⎧-=⎨-+<⎩则方程|()1|2f x c -=-(c 为常数且(1,0)c ∈-)的不同的实数根的个数为( )A .3B .4C .5D .68.已知函数()2e e xx f x ax =--有且只有一个零点,则实数a 的取值范围为( )A .(],0-∞B .[)0,+∞ C .()()0,11,+∞ D .(]{},01-∞9.已知函数23||,3()(3),3x x f x x x -⎧=⎨->⎩,()(3)6g x f x +-=,则函数()()y f x g x =-的零点个数为( )A .0B .4C .3D .210.若函数()2020xlog x x f x a x ⎧=⎨--≤⎩,>,有且只有一个零点,则a 的取值范围是( ) A .(﹣∞,﹣1)∪(0,+∞) B .(﹣∞,﹣1)∪[0,+∞) C .[﹣1,0)D .[0,+∞)11.已知函数()sin ,02224xx f x x π⎧≤≤⎪=⎨⎪<≤⎩,若函数()()1g x f x kx =--恰有三个零点,则实数k 的取值范围为 ( )A .31,44⎡⎤--⎢⎥⎣⎦B .31,44⎛⎤-- ⎥⎝⎦C .41,34⎛⎫-- ⎪⎝⎭D .41,34⎛⎤-- ⎥⎝⎦12.已知函数()()21,1ln 1,1x x f x x x -≤⎧⎪=⎨->⎪⎩,则方程()()1f f x =根的个数为( )A .3B .5C .7D .9二.填空题13.函数()()2ln 14xf x x =⋅+-的零点个数为_______.14.已知函数32,2()(1),2x f x xx x ⎧≥⎪=⎨⎪-<⎩,若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是________.15.已知函数32ln(2),2,()68,,x x m f x x x x x m +-<<⎧=⎨-+≥⎩若函数()f x 仅有2个零点,则实数m 的取值范围为______. 16.已知函数,0()(1),0xlnx x f x e x x >⎧=⎨+⎩,若函数()()()F x f x c c R =-∈恰有3个零点,则实数c 的取值范围是__.三.解答题(解答应写出文字说明、证明过程或演算步骤) 17.求函数lg y x =和sin y x =的图像的交点个数.18.讨论a 取不同值时,关于x 的方程2|log |1|2|x a -+=的解的个数.19.已知函数()f x =,()3g x ax =-.(1)设函数()()()()25h x f x g x x =+-+,讨论函数()y h x =在区间[]0,2内的零点个数;(2)若对任意[]0,4x ∈,总存在[]02,2x ∈-,使得()()0g x f x =成立,求实数a 的取值范围.20.已知函数2()7f x x mx m =++-,m R ∈.(1)若()f x 在区间[]2,4上单调递增,求m 的取值范围; (2)求()f x 在区间[]1,1-上的最小值()g m ; (3)讨论()f x 在区间[]3,3-上的零点个数.21.已知函数()22,182,1x a x f x ax x a x ⎧-≤=⎨-+>⎩,其中a R ∈.()1当1a =时,求()f x 的最小值; ()2当2a ≤时,讨论函数()f x 的零点个数.22.已知函数()34ln f x x x x=--. (1)求()f x 的单调区间;(2)判断()f x 在(]0,10上的零点的个数,并说明理由.(提示:ln10 2.303≈)《函数与方程》(二)解析1.【解析】若260x x --=.则2x =-或3x =.又∵0x ≤∴2x =- 若3ln 0x -+=,则3x e =满足0x >,综上,函数()f x 的零点个数为2. 故选:B2.【解析】当0x >时,3|ln |30,ln 3,x x x e -=∴=±∴=或3e -,都满足0x >; 当0x ≤时,222430,2430,20,164230x x x x ---=∴++=>∆=-⨯⨯<,所以方程没有实数根.综合得函数()3y f x =-的零点个数是2.故选:B3.【解析】函数()ln 1f x x x =-+的零点个数等价于函数ln y x =与函数1y x =-的图象的交点个数.在同一坐标系下作出函数ln y x =与1y x =-的图象,如下图:因为1(ln )y x x ''==,曲线ln y x =在点(1,0)处的切线的斜率为:11k x==, 所以曲线ln y x =在点(1,0)处的切线方程为1y x =-,所以可知两函数图象有一个交点,故函数()ln 1f x x x =-+的零点个数为1. 故选:B .4.【解析】因为()()y f x x R =∈为周期为2的函数,通过且(1,1]x ∈-时,2()f x x =,做出函数图象如图所示:4()log ||y f x x =-的零点个数即为()y f x =与4log ||y x =图象交点个数,由图象可知共有6个交点.故选:B.5.【解析】令()sin 10f x x x =-=,显然0x =不是函数的零点,可得1sin x x=. 故作出函数sin y x =和1y x =的图象,如图所示:在(,)22ππ-上有2个交点.故选:A6.【解析】函数()22lg 2||f x x x x =+-的零点个数,即方程22lg 2||x x x =-+的根的个数,考虑()()22lg ,2||g x x h x x x ==-+,定义在()(),00,-∞+∞的偶函数,当0x >时,()()22lg ,2g x x h x x x ==-+,作出函数图象:两个函数一共两个交点,即当0x >时22lg 2||x x x =-+有两根, 根据对称性可得:当0x <时22lg 2||x x x =-+有两根, 所以22lg 2||x x x =-+一共4个根,即函数()22lg 2||f x x x x =+-的零点的个数为4.故选:C7.【解析】由|()1|2f x c -=-,得()1(2)f x c =±-.∵(1,0)c ∈-, ∴1(2)(3,4),1(2)(2,1)c c +-∈--∈--. 作出函数()f x 和1(2)y c =±-的图象如图所示,易知它们的图象共有4个不同的交点,即方程|()1|2f x c -=-(c 为常数且(1,0)c ∈-)有4个不同的实数根.故选:B8.【解析】(0)1100f =--=,则可知0x =一定是函数()f x 的一个零点0x ≠时,可得:1x x e a x e -=,令1(),()x x e a g x h x x e -==,21()x x xe e g x x '-+=,令()1x x u x xe e =-+, ()xu e x x '=,可得函数()u x 在0x =时取得极小值即最小值 ,()()00u x u ∴≥=.())'0(0g x x ∴>≠.∴函数()g x 在(,0)-∞和(0,)+∞上单调递增,此时,()0g x >恒成立,对于()xa h x e =, 0a <时 , 函数()g x 与()h x 没有交点,如下图,满足条件0a =时 , 函数()g x 与()h x 没有交点,如下图,满足条件1a =时 , 函数1()x h x e=, 经过()0,1, 与函数()g x 的图象没有交点, 如下图,满足条件 .0a >, 且1a ≠时 , 函数()h x 与函数()g x 的图象有交点,如下图,不满足条件,舍去 .综上可得:实数a 的取值范围为{}(],01-∞⋃,故选:D .9.【解析】由()6(3)g x f x =--,知()()()(3)6y f x g x f x f x =-=+--. 令()()(3)F x f x f x =+-,则(3)(3)()F x f x f x -=-+, 所以(3)()F x F x -=,即()F x 的图象关于直线32x =对称.当302x时,()()(3)33(3)3F x f x f x x x =+-=-+--=; 当0x <时,2221()()(3)3(33)32F x f x f x x x x x x ⎛⎫=+-=++--=++=++⎪⎝⎭114.作出()F x 的图象可知,函数()6F x =的解有2个,所以函数()()y f x g x =-的零点个数2个.故选:D10.【解析】当x >0时,因为log 21=0,所以有一个零点,所以要使函数()2020x log x x f x a x ⎧=⎨--≤⎩,>,有且只有一个零点,则当x ≤0时,函数f (x )没有零点即可,当x ≤0时,0<2x ≤1,∴﹣1≤﹣2x <0,∴﹣1﹣a ≤﹣2x ﹣a <﹣a ,所以﹣a ≤0或﹣1﹣a >0,即a ≥0或a <﹣1.故选:B11.【解析】当24x <≤时,y =,则0y ≤,等式两边平方得2268y x x =-+-,整理得()2231x y -+=,所以曲线)24y x =<≤表示圆()2231x y -+=的下半圆,如下图所示:由题意可知,函数()y g x =有三个不同的零点,等价于直线1y kx =+与曲线()y f x =的图象有三个不同交点,直线1y kx =+过定点()0,1P ,当直线1y kx =+过点()4,0A 时,则410k +=,可得14k =-; 当直线1y kx =+与圆()2231x y -+=相切,且切点位于第三象限时,k0<,1=,解得34k =-.由图象可知,当3144k -<≤-时,直线1y kx =+与曲线()y f x =的图象有三个不同交点.因此,实数k 的取值范围是31,44⎛⎤-- ⎥⎝⎦. 故选:B.12.【解析】令()u f x =,先解方程()1f u =. (1)当1u ≤时,则()211f u u =-=,得11u =;(2)当1u >时,则()()ln 11f u u =-=,即()ln 11u -=±,解得211u e=+,31u e =+. 如下图所示:直线1u =,11u e=+,1u e =+与函数()u f x =的交点个数为3、2、2, 所以,方程()1f f x ⎡⎤=⎣⎦的根的个数为3227++=.故选:C. 13.【解析】令()()2ln 140xf x x =⋅+-=,则()24ln 122x x x -+==, 在同一直角坐标系中作出函数()ln 1y x =+与22xy -=的图象,如图:由图象可知,函数()ln 1y x =+当1x →-时,()ln 1y x =+→+∞则与22xy -=的图象有必有两个交点, 所以方程()24ln 122xxx -+==有两个不同实根,所以函数()()2ln 14x f x x =⋅+-的零点个数为2.故答案为:2.14.【解析】作出函数()f x 的图象,如图所示,由图象可知,当01k <<时,函数()f x 与y k =的图象有两个不同的交点, 此时,方程有两个不同实根,所以所求实数k 的取值范围是(0,1).故答案为:(0,1) 15.【解析】对于函数3268y x x x =-+,23128y x x '=-+,令0y '=,解得23x =±,故当,2x ⎛∈-∞- ⎝⎭时,0y '>;当22x ⎛∈ ⎝⎭时,0y '<;当2x ⎛⎫∈+∞ ⎪ ⎪⎝⎭时,0y '>; 令ln(2)0x +=,解得1x =-;令32680x x x -+=,解得0x =,2x =或4x =. 作出ln(2)y x =+,3268y x x x =-+的大致图像:观察可知,若函数()f x 仅有2个零点,则24m <≤,故实数m 的取值范围为(]2,4. 16.【解析】当0x >时,函数()f x lnx =单调递增;当0x ≤时,()(1)xf x e x =+,则()(2)x f x e x '=+2x <-时,()0f x '<,20x -<时,()0f x '>,故当0x ≤时,()f x 在(,2)-∞-上单调递减,在(2,0)-上单调递增,所以()f x 在2x =-处取极小值,极小值为2(2)f e --=-;当1x <-时,()(1)0xf x e x =+< 作出函数()f x 的图象如图:函数()()()F x f x c c R =-∈恰有3个零点,等价于函数()f x 与y c =的图象有且仅有3个交点,由图可知,20e c --<<,故答案为:()20,e -- 17.【解析】由1y lgx ==解得10x =,又sin y x =的值域为[]1,1-, 且y lgx =在定义域上单调递增,作出函数sin y x =与y lgx =的图象如图: 由图象可知两个图象的交点个数为3个,18.【解析】令2()|log |1|2|f x x =-+,作出函数()f x 的图象,如图所示,所求问题可转化为函数()f x ,与直线y a =交点的个数问题. 当0a <时,()y f x =与y a =无交点,所以原方程无解; 当0a =时,()y f x =与y a =有两个交点,原方程有2个解; 当0a >时,()y f x =与y a =有四个交点,原方程有4个解.19.【解析】(1)因为()()()()()22511h x fx g x x x a x =+-+=+-+,令()0h x =,则()2110x a x +-+=,当=0x 时,则10=,不符合条件,当0x ≠时,则11a x x-=+ 作函数1y a =-与()102y x x x=+<≤的图象,由图可知:①当12a -<时,即1a >-时,两图象无公共点,则()h x 在区间[]0,2内无零点;②当12a -=时或512a ->时,即32a <-或1a =-时,两图象仅有一个公共点, 则()h x 在区间[]0,2内仅有一个零点; ③当5212a <-≤时,即312a -≤<-时,两图象有两个公共点, 则()h x 在区间[]0,2内有两个零点.(2)当[]0,4x ∈时,[]20,16x ∈,则[]299,25x +∈,所以()f x 的值域是[]3,5; 当[]02,2x ∈-时,设函数()0g x 的值域是M ,依题意,[]3,5M ⊆,①当0a =时,()03g x =-不合题意;②当0a >时,()()[]2,223,23M g g a a =-=---⎡⎤⎣⎦, 由()()2523g g ⎧≥⎪⎨-≤⎪⎩ ,得2352330a a a -≥⎧⎪--≤⎨⎪>⎩,解得4a ≥; ③当0a <时,()()[]2,223,23M g g a a =-=---⎡⎤⎣⎦,由()()2523g g ⎧-≥⎪⎨≤⎪⎩,得2352330a a a --≥⎧⎪-≤⎨⎪<⎩,解得4a ≤-; 综上得,实数a 的取值范围是(][),44,-∞-⋃+∞.20.【解析】(1)由题意,函数2()()7f x x mx m m R =++-∈开口向上,对称轴的方程为2m x =-,若使得函数()f x 在[]2,4上单调递增,则满足122m -≤,解得4m ≥-,即实数m 的取值范围[4,)-+∞.(2)①当112m -≤-即2m ≥时,函数()y f x =在区间[]1,1-单调递增, 所以函数()y f x =的最小值为()()16g m f =-=-;②当1112m -<-<,即22m -<<时, 函数()y f x =在区间11,2m ⎡⎤--⎢⎥⎣⎦单调递减,在区间1,12m ⎡-⎤⎢⎥⎣⎦上单调递增, 所以函数()y f x =的最小值为21()724m g m f m m ⎛⎫=-=-+- ⎪⎝⎭; ③当112m -≥即2m ≤-时,函数()y f x =在区间[]1,1-单调递减, 所以函数()y f x =的最小值为()()126g m g m ==-, 综上可得,函数的最小值为226,27(),2246,2m m m m g m m m -≤-⎧⎪+-⎪=--<<⎨⎪-≥⎪⎩. (3)因为函数()y f x =的对称轴方程为12x m =-,且24280m m ∆=-+>恒成立, ①当()()133232203420m f m f m ⎧-<-<⎪⎪-=-≥⎨⎪=+≥⎪⎩,即112m -≤≤时, 函数()f x 在区间[]3,3-上有2个零点; ②当()1323220m f m ⎧-≤-⎪⎨⎪-=-≥⎩,此时m 不存在; ③当()1323420m f m ⎧-≥⎪⎨⎪=+≥⎩,此时m 不存在;④当()()330f f -⋅≤,即()()22420m m -+≤,解得m 1≥或12m ≤-时,函数()f x 在区间[]3,3-上有1个零点. 综上可得:当112m -≤≤时,函数()f x 在区间[]3,3-上有2个零点, 当m 1≥或12m ≤-时,函数()f x 在区间[]3,3-上有1个零点. 21.【解析】()1当1a =时,()221,182,1x x f x x x x ⎧-≤=⎨-+>⎩,则当1x ≤时,()f x 在(],1-∞上单调递增,()1f x >-且无最小值;当1x >时,由二次函数()()2282414g x x x x =-+=--知,()f x 在(]1,4上单调递减,在()4,+∞上单调递增,故()()min 414f x f ==-.()2当0a ≤,1x ≤时,()f x 没有零点,当1x >时,()f x 没有零点;当02a <≤,1x ≤时,()f x 有一个零点,当1x >时,()f x 有一个零点.22.【解析】(1)由题意知,()f x 的定义域为()0,∞+,则令2223443()10x x f x x x x -+'=+-==, 解得1x =或3x =,当01x <<或3x >时,()0f x '>,则此时()f x 单调递增; 当13x <<时,()0f x '<,则此时()f x 单调递减.故()f x 的单调递增区间是()0,1和()3,+∞,单调递减区间是()1,3.(2)由函数在()0,1上单调递增,在()1,3上单调递减,则当03x <≤时,()()12f x f ≤=-,故()f x 在(]0,3上无零点;又()324ln30f =-<,当310x <≤时,因为3(10)104ln10100.34 2.3030.488010f =--≈--⨯=>, 又()f x 在(]3,10上单调递增,所以()f x 在(]3,10上仅有一个零点.综上,()f x 在(]0,10上的零点的个数为1.。
2014年数学一轮复习试题_函数与方程
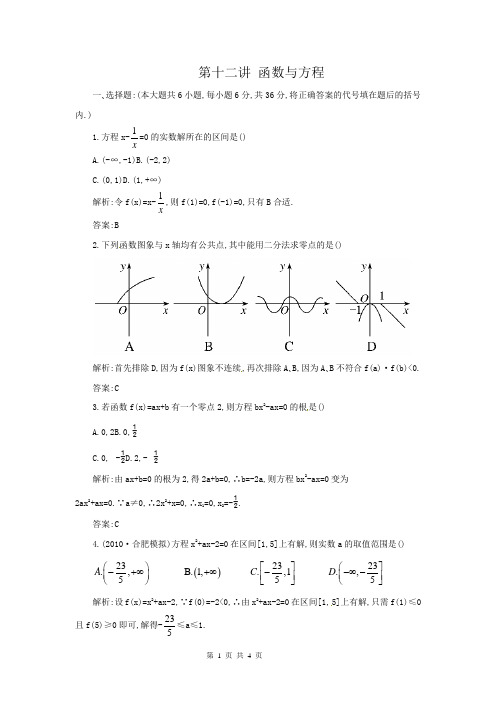
第十二讲 函数与方程一、选择题:(本大题共6小题,每小题6分,共36分,将正确答案的代号填在题后的括号内.)1.方程x-1x=0的实数解所在的区间是() A.(-∞,-1)B.(-2,2) C.(0,1)D.(1,+∞) 解析:令f(x)=x-1x,则f(1)=0,f(-1)=0,只有B 合适. 答案:B2.下列函数图象与x 轴均有公共点,其中能用二分法求零点的是()解析:首先排除D,因为f(x)图象不连续,再次排除A 、B,因为A 、B 不符合f(a)·f(b)<0. 答案:C3.若函数f(x)=ax+b 有一个零点2,则方程bx 2-ax=0的根是() A.0,2B.0, C.0, - D.2,-解析:由ax+b=0的根为2,得2a+b=0,∴b=-2a,则方程bx 2-ax=0变为2ax 2+ax=0.∵a≠0,∴2x 2+x=0,∴x 1=0,x 2=- .答案:C4.(2010·合肥模拟)方程x 2+ax-2=0在区间[1,5]上有解,则实数a 的取值范围是()()232323..,1.,55, B.1,5A C D ⎡⎤⎛⎤---- ⎢⎛⎫+⎥∞+∞∞ ⎪⎣⎭⎦⎝⎝⎥⎦解析:设f(x)=x 2+ax-2,∵f(0)=-2<0,∴由x 2+ax-2=0在区间[1,5]上有解,只需f(1)≤0且f(5)≥0即可,解得-235≤a≤1.答案:C5.已知函数y=f(x)的图象是连续不断的,有如下的对应值表:则函数y=f(x)在x∈[1,6]上的零点至少有()A.5个B.4个C.3个D.2个解析:满足条件的零点应在(1,2)和(4,5)之间,因此至少有两个零点. 答案:D6.(2010·浙江)已知x0是函数f(x)=2x+11x-的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则()A.f(x1)<0,f(x2)<0B.f(x1)<0,f(x2)>0C.f(x1)>0,f(x2)<0D.f(x1)>0,f(x2)>0解析:由于函数g(x)=1111x x=---在(1,+∞)上单调递增,函数h(x)=2x在(1,+∞)上单调递增,故函数f(x)=h(x)+g(x)在(1,+∞)上单调递增,所以函数f(x)在(1,+∞)上只有惟一的零点x0,且在(1,x0)上f(x)<0,在(x0,+∞)上f(x)>0,故选B.答案:B二、填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)7.若函数f(x)=x2+ax+b的两个零点是-2和3,则不等式a·f(-2x)>0的解集是________.解析:由于f(x)=x2+ax+b的两个零点是-2和3,即方程x2+ax+b=0的两个根是-2和3,因此231236a ab b-+=-=-⎧⎧⇒⎨⎨-==-⎩⎩,因此f(x)=x2-x-6,所以不等式a·f(-2x)>0即-(4x2+2x-6)>0,即2x2+x-3<0,解集为{x|- <x<1}.答案:{x|- <x<1}8.(应用题,易)在26枚崭新的金币中,混入了一枚外表与它们完全相同的假币(重量不同),现在只有一台天平,请问:你最多称________次就可以发现这枚假币?答案:49.方程xlg(x+2)=1有________个不同的实数根.解析:由题意知x≠0,∵xlg(x+2)=1,∴lg(x+2)=1x ,画出y=lg(x+2),y=1x的图象(图略),两个函数图象的交点个数即为方程根的个数,由图象知在第一象限和第三象限各有一个交点,故方程有2个不等实数根.答案:210.已知函数f(x)=|x|+|2-x|,若函数g(x)=f(x)-a 的零点个数不为0,则a 的最小值为________.解析:由于f(x)=|x|+|2-x|=22,0,2,02,22, 2.x x x x x -⎧⎪<<⎨⎪-⎩≤≥ 所以f(x)的最小值等于2,要使f(x)-a=0有解,应使a≥2,即a 的最小值为2. 答案:2三、解答题:(本大题共3小题,11、12题13分,13题14分,写出证明过程或推演步骤.) 11.已知二次函数f(x)=ax 2+bx+c.(1)若a>b>c 且f(1)=0,试证明f(x)必有两个零点;(2)若对x 1、x 2∈R 且x 1<x 2,f(x 1)≠f(x 2),方程f(x)= [f(x 1)+f(x 2)]有两个不等实根,证明必有一实根属于(x 1,x 2).证明:(1)∵f(1)=0,∴a+b+c=0.又∵a>b>c,∴a>0,c<0,即ac<0.又∵Δ=b 2-4ac≥-4ac>0,∴方程ax 2+bx+c=0有两个不等实根,所以函数f(x)有两个零点.(2)令g(x)=f(x)- [f(x 1)+f(x 2)],则g(x 1)=f(x 1)- [f(x 1)+f(x 2)] =12()()2f x f x -()()()()222112g x f x y f x f ()()x 2f x f x =-+⎡-=⎤⎣⎦,()()122121()(g x g )()()22x f x f x f x f x --=⋅∴()()212 f x f 14x .-⎡⎤⎣⎦=-∵f(x 1)≠f(x 2),∴g(x 1)•g(x 2)<0.∴g(x)=0在(x 1,x 2)内必有一实根.评析:可将方程根的问题转化成函数零点的问题,借助函数的图象和性质进行解答. 12.若函数f(x)=22x+2xa+a+1有零点,求实数a 的取值范围. 解:依题意,方程22x+2x a+a+1=0有实数根. 令2x=t (t>0),则t 2+at+a+1=0,2222211(1)2(1)222,(1)2,(1)11111112,22a 11a a t t t t t t t t t t t t t t t +++-++-==++-+++++++++=---++∴∴由于≥≥故的取值范围是≤≤13.(1)m 为何值时,f(x)=x 2+2mx+3m+4.①有且仅有一个零点;②有两个零点且均比-1大;(2)若函数f(x)=|4x-x 2|+a 有4个零点,求实数a 的取值范围.解:(1)①f(x)=x 2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根⇔Δ=0, 即4m 2-4(3m+4)=0,即m 2-3m-4=0,∴m=4或m=-1.②解法一:设f(x)的两个零点分别为x 1,x 2.则x 1+x 2=-2m,x 1•x 2=3m+4. 由题意,知()()()()()21212234041,4m 43m 40x 1x 10x 1x 102201,342105,m m m m m m m m m -->><-⎧⎧⎪⎪-+⎧-+>⎪∆=+++>⇒⎨⎪+>⇒<⎨⎨⎪⎪+-+>>-+>⎩⎩⎩或 ∴-5<m<-1.故m 的取值范围为(-5,-1). 解法二:由题意,知0,2340,1,1,(1)0,12340.m m m m f m m >-->⎧⎧⎪⎪->-<⎨⎨⎪⎪->+>∆-+⎩⎩即∴-5<m<-1.∴m 的取值范围为(-5,-1). (2)令f(x)=0,得|4x-x 2|+a=0,即|4x-x 2|=-a. 令g(x)=|4x-x 2|,h(x)=-a.作出g(x)、h(x)的图象. 由图象可知,当0<-a<4,即-4<a<0时,g(x)与h(x)的图象 有4个交点,即f(x)有4个零点. 故a 的取值范围为(-4,0).。
高考数学大一轮复习配套课时训练:第二篇 函数、导数及其应用 第8节 函数与方程(含答案)

第8节函数与方程课时训练练题感提知能【选题明细表】A组一、选择题1.(2013惠阳一中实验学校模拟)函数f(x)=-log2x的零点所在的区间为( C )(A)(,) (B)(,1)(C)(1,2) (D)(2,3)解析:f(x)在(0,+∞)上是减函数,且f(1)=1>0,f(2)=-1=-<0,则f(x)的零点在区间(1,2)内.故选C.2.(2013山东莱州一中月考)函数f(x)=ln x+e x的零点所在的区间是( A )(A)(0,) (B)(,1) (C)(1,e) (D)(e,+∞)解析:函数f(x)=ln x+e x在(0,+∞)上单调递增,F()=ln +=-1+>0,结合选项知应选A.3.(2013山东临沂市模拟)函数f(x)=x-2-x的零点个数为( B )(A)0 (B)1 (C)2 (D)3解析:由f(x)=x-2-x=0得x=()x,在同一坐标系中作出函数y=x,y=()x 的图象,由图象可知两函数的交点有1个,即函数f(x)=x-2-x的零点个数为1.故选B.4.函数f(x)=的零点个数为( C )(A)0 (B)1 (C)2 (D)3解析:当x≤0时,令x2+2x-3=0,解得x=-3或x=1(舍去),当x>0时,令-2+ln x=0,解得x=e2,所以函数f(x)有2个零点,故选C.5.(2013年高考重庆卷)若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间( A )(A)(a,b)和(b,c)内(B)(-∞,a)和(a,b)内(C)(b,c)和(c,+∞)内(D)(-∞,a)和(c,+∞)内解析:∵a<b<c,∴f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,∴f(a)f(b)<0,f(b)f(c)<0,故选A.6.(2013年高考湖南卷)函数f(x)=ln x的图象与函数g(x)=x2-4x+4的图象的交点个数为( C )(A)0 (B)1 (C)2 (D)3解析:g(x)=x2-4x+4=(x-2)2,在同一平面直角坐标系内画出函数f(x)=ln x与g(x)=(x-2)2的图象(如图).由图可得两个函数的图象有2个交点.故选C.7.(2013湛江市高考测试)函数f(x)=(x-1)cos x2在区间[0,4]上的零点个数是( C )(A)4 (B)5 (C)6 (D)7解析:由f(x)=0得x=1或cos x2=0,由cos x2=0,得x2=kπ+(k∈Z);又x∈[0,4],因此0≤x2=kπ+≤16,-≤k≤-,因此整数k可取0,1,2,3,4,因此f(x)在[0,4]上的零点个数是6,故选C.二、填空题8.(2013山东枣庄一模)函数f(x)=的零点的个数为.解析:当x≥0时,由f(x)=0得x+1=0,此时x=-1不成立.当x<0时,由f(x)=0得x2+x=0,此时x=-1或x=0(不成立舍去).所以函数的零点为x=-1.答案:19.(2013惠州市高三第一次模拟)已知函数f(x)=3x+x-9的零点为x0,则x0所在区间为.解析:f()=+-9<0,F()=+-9<0,f()=+-9>0.答案:[,]10.(2013惠州市二调)若函数f(x)=|4x-x2|-a有3个零点,则a= .解析:作出函数y=|4x-x2|的图象如图所示,若f(x)有3个零点,则函数y=|4x-x2|与函数y=a的图象有3个交点,由图知a=4.答案:411.(2013山东即墨市期末)已知函数f(x)=且关于x的方程f(x)-a=0有两个实根,则实数a的取值范围是.解析:f(x)的图象如图,要使方程f(x)-a=0有两个实根,即y=f(x)与y=a的图象有两个交点,0<a≤1.答案:(0,1]三、解答题12.判断函数f(x)=1+4x+x2-x3在区间(-1,1)内零点的个数,并说明理由.解:∵f(-1)=1-4+1+=-<0,f(1)=1+4+1-=>0,∴f(x)在区间(-1,1)内有零点.又f'(x)=4+2x-2x2=-2(x+1)(x-2),当-1<x<1时,f'(x)>0,∴f(x)在(-1,1)内单调递增,因此,f(x)在(-1,1)内有且仅有一个零点.13.已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.解:f(x)=4x+m·2x+1有且仅有一个零点,即方程(2x)2+m·2x+1=0仅有一个实根,设2x=t(t>0),则t2+mt+1=0仅有一个正实根.当Δ=0时,m2-4=0,解得m=2或m=-2,而m=-2时,t=1;m=2时,t=-1(不合题意,舍去),∴2x=1,x=0符合题意.当Δ>0,即m>2或m<-2时,t2+mt+1=0有两正根或两负根,即f(x)有两个零点或没有零点.∴这种情况不符合题意.综上可知,m=-2时,f(x)有唯一零点,该零点为0.B组14.(2013广东广州一模)已知e是自然对数的底数,函数f(x)=e x+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,则下列不等式成立的是( A )(A)f(a)<f(1)<f(b) (B)f(a)<f(b)<f(1)(C)f(1)<f(a)<f(b) (D)f(b)<f(1)<f(a)解析:函数f(x),g(x)均为定义域上的单调递增函数,且f(0)=-1<0,f(1)=e-1>0,g(1)=-1<0,g(e)=e-1>0,所以a∈(0,1),b∈(1,e),即a<1<b,所以f(a)<f(1)<f(b).故选A.15.(2013梅州市质检)设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为( C )(A)(-∞,-2] (B)[-1,0](C)(-,-2] (D)(-,+∞)解析:由题意可得x2-3x+4=2x+m在x∈[0,3]上有两个不同的根,即函数y=m,y=x2-5x+4,x∈[0,3]的图象有两个不同的交点,作出函数图象如图,由图可知,当-<m≤-2时满足要求,故选C.16.(1)已知f(x)=x2+2mx+3m+4,m为何值时.①函数有且仅有一个零点;②函数有两个零点且均比-1大;(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.解:(1)①f(x)=x2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根⇔Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.②法一设f(x)的两个零点分别为x1,x2,则x1+x2=-2m,x1·x2=3m+4. 由题意,知⇔⇔∴-5<m<-1.故m的取值范围为(-5,-1). 法二由题意,知即∴-5<m<-1.∴m的取值范围为(-5,-1).(2)令f(x)=0,得|4x-x2|+a=0,即|4x-x2|=-a.令g(x)=|4x-x2|,h(x)=-a. 作出g(x)、h(x)的图象.由图象可知,当0<-a<4,即-4<a<0时,g(x)与h(x)的图象有4个交点, 即f(x)有4个零点.故a的取值范围为(-4,0).。
2021版《大高考》高考数学(理)一轮总复习模拟创新题:第2章 第7节函数与方程

全国新课标区模拟精选题:依据高考命题大数据分析,重点关注基础题2,4,力量题9,13. 专项基础测试 模拟精选题 一、选择题1.(2022·陕西西安模拟)已知函数f (x )=⎩⎨⎧2x -1,x ≤1,1+log 2x ,x >1,则函数f (x )的零点为( )A.12,0B.-2,0C.12D.0解析 当x ≤1时,由f (x )=2x -1=0,得x =0;当x >1时,由f (x )=1+log 2x =0,解得x =12,又由于x >1,所以此时方程无解,函数f (x )的零点只有0.故选D. 答案 D2.(2022·黑龙江佳木斯模拟)已知符号函数sgn(x )=⎩⎨⎧1,x >0,0,x =0,-1,x <0.则函数f (x )=sgn(ln x )-ln x 的零点个数为( ) A.1B.2C.3D.4解析依题意得f (x )=⎩⎪⎨⎪⎧1-ln x ,x >1,0,x =1,-1-ln x ,0<x <1,令f (x )=0得x =e ,1,1e ,所以函数有3个零点,故选C. 答案 C3.(2021·青岛市模拟)函数f (x )=ln(x +1)-2x 的零点所在的大致区间是( ) A.(0,1)B.(1,2)C.(2,e)D.(3,4)解析 利用零点存在性定理得到f (1)·f (2)=(ln 2-2)·(ln 3-1)<0,故选B. 答案 B4.(2021·济宁高三期末)设x 1,x 2是方程ln|x -2|=m (m 为实常数)的两根,则x 1+x 2的值为( )A.4B.2C.-4D.与m 有关解析 方程ln|x -2|=m 的根即函数y =ln|x -2|的图象与直线y =m 的交点的横坐标,由于函数y =ln|x -2|的图象关于x =2对称,且在x =2两侧单调,值域为R ,所以对任意的实数m ,函数y =ln|x -2|的图象与直线y =m 必有两交点,且两交点关于直线x =2对称,故x 1+x 2=4,选A. 答案 A 二、填空题5.(2022·江西十校二联)给定方程⎝ ⎛⎭⎪⎫12x +sin x -1=0,下列命题中:①方程没有小于0的实数解; ②方程有很多个实数解;③方程在(-∞,0)内有且只有一个实数解; ④若x 0是方程的实数解,则x 0>-1. 正确命题是________.解析 在同一坐标系中画出函数y =⎝ ⎛⎭⎪⎫12x-1与y =-sin x (该函数的值域是[-1,1])的大致图象,结合图象可知,它们的交点中,横坐标为负的交点,有且只有一个,因此方程⎝ ⎛⎭⎪⎫12x+sin x-1=0在(-∞ ,0)内有且只有一个实数解,故③正确,①不正确,由图象易知②,④均正确. 答案 ②③④ 三、解答题6.(2021·长春模拟)设函数f (x )=x +1x 的图象为C 1,C 1关于点A (2,1)对称的图象为C 2,C 2对应的函数为g (x ).(1)求g (x )的解析式;(2)若直线y =m 与C 2只有一个交点,求m 的值和交点坐标.解 (1)设点P (x ,y )是C 2上的任意一点,则P (x ,y )关于点A (2,1)对称的点为P ′(4-x ,2-y ),代入f (x )=x +1x ,可得2-y =4-x +14-x,即y =x -2+1x -4,∴g (x )=x -2+1x -4. (2)由⎩⎪⎨⎪⎧y =m ,y =x -2+1x -4,消去y 得x 2-(m +6)x +4m +9=0,Δ=[-(m +6)]2-4(4m +9), ∵直线y =m 与C 2只有一个交点, ∴Δ=0,解得m =0或m =4.当m =0时,经检验合理,交点为(3,0); 当m =4时,经检验合理,交点为(5,4). 创新导向题利用函数零点个数求参数取值范围7.函数y =|x 2-1|x -1-kx 恰有两个零点,则实数k 的范围是( )A.(0,1)B.(0,1)∪(1,2)C.(1,+∞)D.(-∞,2)解析 令y =0,得|x 2-1|x -1=kx ,令y 1=|x 2-1|x -1(x ≠1),y 2=kx ,则y 1=⎩⎪⎨⎪⎧x +1,x <-1或x >1,-x -1,-1≤x <1,图象如图所示,y 2=kx 表示过点(0,0)的直线,∴由题意及图可知k 的取值范围是(0,1)∪(1,2),故选B.答案 B 专项提升测试 模拟精选题 一、选择题8.(2022·湖北荆门模拟)对于函数f (x )=x 2+mx +n ,若f (a )>0,f (b )>0,则函数f (x )在区间(a ,b )内( )A.肯定有零点B.肯定没有零点C.可能有两个零点D.至多有一个零点解析 利用排解法,f (a )·f (b )<0是函数f (x )在区间(a ,b )内有零点的充分不必要条件,故选C. 答案 C9.(2021·湖南衡阳模拟)设方程2x +x +2=0和方程log 2x +x +2=0的根分别为p 和q ,设函数f (x )=(x +p )(x +q )+2,则( ) A.f (2)=f (0)<f (3) B.f (0)<f (2)<f (3) C.f (3)<f (2)=f (0)D.f (0)<f (3)<f (2)解析 ∵方程2x +x +2=0和方程log 2 x +x +2=0的根分别为函数y =2x ,y =log 2 x 与直线y =-x -2的交点横坐标,而函数y =2x ,y =log 2 x 互为反函数,其图象关于y =x 对称,又直线y =-x -2与直线y =x 垂直,且两直线的交点坐标为(-1,-1),∴p +q =-2, 则f (x )=x 2+(p +q )x +pq +2=x 2-2x +pq +2, ∵该二次函数的对称轴为x =1,∴f (2)=f (0)<f (3).故选A. 答案 A 二、填空题10.(2022·天津南开中学模拟)已知函数f (x )=⎩⎨⎧2x -1,x >0,-x 2-2x ,x ≤0,若函数g (x )=f (x )-m 有3个零点,则实数m 的取值范围是________.解析 f (x )=⎩⎪⎨⎪⎧2x -1,-x 2-2x=⎩⎪⎨⎪⎧2x -1,x >0,-(x +1)2+1,x ≤0,图象如图:由g (x )=f (x )-m 有3个零点,知f (x )=m 有三个根,则实数m 的范围是(0,1).答案 (0,1)11.(2022·广西南宁模拟)已知函数f (x )=a x +x -b 的零点x 0∈(n ,n +1)(n ∈Z )其中常数a ,b 满足2a =3,3b =2,则n =________.解析 a =log 23>1,b =log 32<1,令f (x )=0,得a x=-x +b ,在同一坐标系中画出函数y =ax和y =-x +b 的图象,如图所示;由图可知,两函数的图象在区间(-1,0)内有交点,所以函数f (x )在区间(-1,0)内有零点,所以n =- 1.答案 -1 三、解答题12.(2021·青岛模拟)已知函数f (x )=|x 2-4x +3|.若关于x 的方程f (x )-a =x 至少有三个不相等的实数根,求实数a 的取值范围.解 f (x )=⎩⎨⎧(x -2)2-1,x ∈(-∞,1]∪[3,+∞),-(x -2)2+1,x ∈(1,3),作出图象如图所示.原方程变形为|x 2-4x +3|=x +a .于是,设y =x +a ,在同一坐标系下再作出y =x +a 的图象.如图.则当直线y =x +a 过点(1,0)时a =-1;当直线y =x +a 与抛物线y =-x 2+4x -3相切时, 由⎩⎨⎧y =x +a ,y =-x 2+4x -3⇒x 2-3x +a +3=0. 由Δ=9-4(3+a )=0,得a =-34.由图象知当a ∈⎣⎢⎡⎦⎥⎤-1,-34时方程至少有三个不等实根.创新导向题利用方程根的个数和函数性质求参数取值范围13.函数f (x )是定义在R 上的偶函数,且满足f (x +2)=f (x ),当x ∈[0,1]时,f (x )=2x ,若在区间[-2,3]上方程ax +2a -f (x )=0恰有四个不相等的实数根,则实数a 的取值范围是________. 解析 由f (x +2)=f (x )得函数f (x )的周期是2,作出函数y =f (x ),y =ax +2a 的部分图象,如图,要使方程ax +2a -f (x )=0恰有四个不相等的实数根,则直线y =ax +2a =a (x +2)的斜率a 满足k AH <a <k AG ,由题意可知G (1,2),H (3,2),A (-2,0),所以k AH =25,k AG =23,所以25<a <23.答案 ⎝ ⎛⎭⎪⎫25,23。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学轮函数与方程训练题
1.函数fx=x-cos x在[0,+内
A.没有零点
B.有且仅有一个零点
C.有且仅有两个零点
D.有无穷多个零点
解析:在同一直角坐标系中分别作出函数y=x和y=cos x的图象,如图,由于x1时,y=x1,y=cos x1,所以两图象只有一个交点,即方程x-cos x=0在[0,+内只有一个根,
所以fx=x-cos x在[0,+内只有一个零点,所以选B.
答案:B
2.2021吉林白山二模已知函数fx=2mx2-x-1在区间-2,2上恰有一个零点,则m的取
值范围是
A.-38,18
B.-38,18
C.-38,18
D.-18,38
解析:当m=0时,函数fx=-x-1有一个零点x=-1,满足条件.当m0时,函数
fx=2mx2-x-1在区间-2,2上恰有一个零点,需满足①f-2f20,或
②f-2=0,-20,或③f2=0,02.
解①得-18
答案:D
3.已知函数fx满足fx+1=fx-1,且fx是偶函数,当x[0,1]时,fx=x,若在区间[-
1,3]上函数gx=fx-kx-k有4个零点,则实数k的取值范围是________.
解析:由fx+1=fx-1得,
fx+2=fx,则fx是周期为2的`函数.
∵fx是偶函数,当x[0,1]时,fx=x,
当x[-1,0]时,fx=-x,
易得当x[1,2]时,fx=-x+2,
当x[2,3]时,fx=x-2.
在区间[-1,3]上函数gx=fx-kx-k有4个零点,即函数y=fx与y=kx+k的图象在区间[-1,3]上有4个不同的交点.作出函数y=fx与y=kx+k的图象如图所示,结合图形易知k0,14].
答案:0,14]
4.1m为何值时,fx=x2+2mx+3m+4.①有且仅有一个零点;②有两个零点且均比-1大;
2若函数fx=|4x-x2|+a有4个零点,求实数a的取值范围.
解:1①函数fx有且仅有一个零点方程fx=0有两个相等实根=0,即4m2-43m+4=0,即m2-3m-4=0,m=4或m=-1.
②设fx有两个零点分别为x1,x2,
则x1+x2=-2m,x1x2=3m+4.
由题意,有=4m2-43m+40x1+1x2+10 x1+1+x2+10
m2-3m-403m+4-2m+10-2m+2m4或m-1,m-5,m1,
-5
2令fx=0,
得|4x-x2|+a=0,
即|4x-x2|=-a.
令gx=|4x-x2|,
hx=-a.
作出gx、hx的图象.
由图象可知,当04,即-4
故a的取值范围为-4,0.
感谢您的阅读,祝您生活愉快。
