暂态分析习题课分解
暂态分析部分习题答案
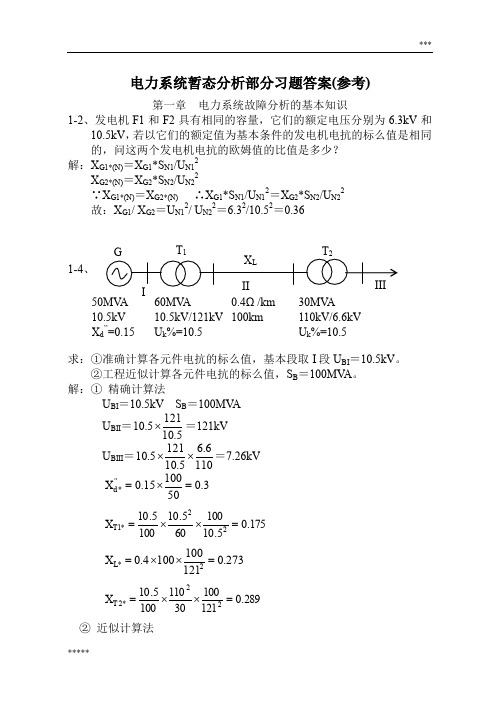
电力系统暂态分析部分习题答案(参考)第一章 电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量，它们的额定电压分别为6.3kV 和10.5kV ，若以它们的额定值为基本条件的发电机电抗的标么值是相同的，问这两个发电机电抗的欧姆值的比值是多少？ 解：X G1*(N)＝X G1*S N1/U N12 X G2*(N)＝X G2*S N2/U N22∵X G1*(N)＝X G2*(N) ∴X G1*S N1/U N12＝X G2*S N2/U N22 故：X G1/ X G2＝U N12/ U N22＝6.32/10.52＝0.361-4、求：①准确计算各元件电抗的标么值，基本段取I 段U BI ＝10.5kV 。
②工程近似计算各元件电抗的标么值，S B ＝100MV A 。
解：① 精确计算法U BI ＝10.5kV S B ＝100MV AU BII ＝5.101215.10⨯＝121kVU BIII ＝1106.65.101215.10⨯⨯＝7.26kV 3.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法50MV A 10.5kV X d ’’=0.15 60MV A 10.5kV/121kV U k %=10.5 0.4Ω/km 100km 30MV A 110kV/6.6kV U k %=10.5U B ＝U av S B ＝100MV A3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X1-5、某一线路上安装一台Xk%＝5的电抗器，其额定电流为150A ，额定电压为6kV ，若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它，并要求保持线路的电抗欧姆值不变，问这台电抗器的电抗百分数值应是多少？ 解：∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、(1) 若短路前空载，计算短路电流的周期分量及短路电流最大有效值； (2) 若A 相非周期分量电流的初值为零及最大时，计算相应的B 、C 相非周期分量电流的初始值；(3) 若短路前变压器满负荷运行，功率因数为0.9（低压侧），计算最大非周期分量电流的初始值，并与空载时短路比较。
最新5电路的暂态分析教学讲义ppt课件
圆，轻巧又便宜的蒲扇。 蒲扇流传至今，我的记忆中，它跨 越了半 个世纪 ，
也走过了我们的半个人生的轨迹，携 带着特 有的念 想，一 年年， 一天天 ，流向 长
长的时间隧道，袅
5电路的暂态分析
概述
“稳态(steady state)”与 “暂态(transient state)”的概念:
KR
R
+
E
_
16
解：
2
K
R
i i2
i + 1 2k E
R1 R2
1 2k 1k
_ 6V
uL
uC
换路前的等效电路
+ R R1 R2
_E
i1 u C
E iL(0)i1(0)RR11.5mA
u C (0 ) i1 (0 ) R 1 3V17
i t=0 + 时的等效电路
i2
i1(0)iL(0)iL(0) 1.5mA
研究过渡过程的意义：过渡过程是一种自然现 象， 对它的研究很重要。过渡过程的存在有利有弊。 有利的方面，如电子技术中常用它来产生各种波形； 不利的方面，如在暂态过程发生的瞬间，可能出现过 压或过流，致使设备损坏，必须采取防范措施。
7
§5.1 换路定理(law of switch) 与电压和电流初始值的确定
是那么凉快，那么的温馨幸福，有母 亲的味 道！
蒲扇是中国传统工艺品，在
我国已有三千年多年的历史。取材于 棕榈树 ，制作 简单， 方便携 带，且 蒲扇的 表
面光滑，因而，古人常会在上面作画 。古有 棕扇、 葵扇、 蒲扇、 蕉扇诸 名，实 即
今日的蒲扇，江浙称之为芭蕉扇。六 七十年 代，人 们最常 用的就 是这种 ，似圆 非
工学第3章暂态分析课件
C
_
零，故电容元件在直流电路视为开路。
将上式两边同乘上 u，并积分，则得： 电容元件
t
udit
uCduu1C2u
0
0
2
电场能 W 1 Cu2
2
即电容将电能转换为电场能储存在电容中，当电压
增大时，电场能增大，电容元件从电源取用电能；
当电压减小时，电场能减小，电容元件向电源放还
能量。电容元件不工消学耗第能3量章，暂是态储能元件。
合S后：电流 i 随电压 u 比例变化。
所以电阻电路不存在暂态过程 (R耗能元件)。
工学第3章暂态
电容元件
+
U
-
S
R
iC
C
+
-
uC
uC
U
暂态
o
(b)
t
图(b)
合S前: iC 0 , uC 0
稳态
合S后： u C 由零逐渐增加到U i C du
所以电容电路存在暂态过程
dt
工学第3章暂态
电感电路 KR
工学第3章暂态
2. 换路定则 换路: 电路状态的改变。如：
1 . 电路接通、断开电源 2 . 电路中电源的升高或降低 3 . 电路中元件参数的改变
…………..
工学第3章暂态
换路定则: 在换路瞬间，电容上的电压、 电感中的电流不能突变。
设：t=0 — 表示换路瞬间 (定为计时起点)
t=0-— 表示换路前的终了瞬间 t=0+—表示换路后的初始瞬间（初始值）
电容元件
u
电容器的电容与极板的尺寸及其间介质的
介电常数等关。
C S (F)
d
S — 极板面积（m2） d —板间距离（m） ε—介电常数（F/m）
电力系统暂态分析-部分习题答案汇编
U B1 =10.5kV ，1 B130 3 10.5 = 1.65kAU B 2 =115kV ， I B1 30 3 115=0.15kA第一章电力系统分析基础知识 1-2-1对例1-2，取U B 2 =110kV , S B =30MVA ,用准确和近似计算法计算参数标幺值。
解：①准确计算法：选取第二段为基本段，取 U B 2 =110kV ，S B =30MVA ，则其余两段的电压基准值分 电流基准值:各元件的电抗标幺值分别为: 发电机： 10.52 30 C"x 1..- 0.262 - 0.32 30 9.52输电线路：x^ =0.4 80 鲨=0.0791102变压器T 2 :211030 c 一 X 4” =0.10522 =0.211521102电抗器：X 5 =0.05 62.62 _ 0.4 6.6 0.330电缆线路： 心.=0.08 2.5 一 =0.146.6 11电源电动势标幺值：E 1.169.5②近似算法：取S B =30MVA ，各段电压电流基准值分别为:别为： 10 5U B 1 - k 1U B2110kV _9.5kV 121k2册"6kV6.6B1B2S B30、3U B1S B一，3U B23 9.5 30、3 110= 1.8kA= 0.16kA变压器T 1 : X 2 =0.105 1212 1102 3031.52= 0.121U B2U B330U B3 = 6.3kV , I BI 2.75kA.3 6.3各元件电抗标幺值：发电机：2…10.5 30 c* x,”=0.26 2=0.2630 10.52变压器T1:121230 x2.. =0.105 20.11115231.5输电线路：30x3=0.4 80 2- 0.073115变压器T2:115230X4 “ = 0.105 20.21115 15电抗器：X5 =0.05 — ----- =0.44—.3 0.330电缆线路：x—=0.08 2.5 —=0.1516.3211电源电动势标幺值：E 1.0510.5发电机：为=0.26 匹色耳=0.3230 9.5变压器T1:121230x2.. =0.105 2厂0.121 2110231.52输电线路：30x3=0.4 80 2=0.079 31102110 30变压器T2 : X4：-0.105 一r—-0.211521102电抗器：x - 0.05 — 2.62 = 0.46.6 0.3电缆线路：冷皿25囂2心411电源电动势标幺值：E 1.169.5 1-3-1在例1-4中，若6.3kV母线的三相电压为: Ua - 2 6.3c o s《t ；：匚)U a = 2 6.3cos( s t ： -120)Ua = 2 6.3cos( it 乜-120)在空载情况下f 点突然三相短路，设突然三相短路时 :.=30 o试计算：（1） 每条电缆中流过的短路电流交流分量幅值； （2） 每条电缆三相短路电流表达式；（3） 三相中哪一相的瞬时电流最大，并计算其近似值； （4） 为多少度时，a 相的最大瞬时电流即为冲击电流。
[工学]第三章 电路的暂态分析(1)
![[工学]第三章 电路的暂态分析(1)](https://img.taocdn.com/s3/m/d81820fca8956bec0875e3a5.png)
换路瞬间i1＝iC
h
返回10
哼哼，地府又多了一个小鬼…
你的选择 是错误
的！！！
h
题解 习题 11
通往天堂的班车已到站， 恭喜你!
题解 习题
h
12
S
R1
i1 iC
+
i2
+
－US
C －uuCCR2
解：
∵t ＝0－，电路稳态。 C 相当于开路，
i1(0－ )= i2(0－ )=US/(R1+R2) = 2mA
返回
h
16
一、零输入响应
如果在换路瞬间储能元件原来就有 能量储存，那么即使电路中并无外施电 源存在，换路后电路中仍将有电压电流， 这是因为储能元件要释放能量。
因此，将电路中无输入信号作用时， 由电路内部在初始时刻的储能所产生的 响应称为零输入响应。
h
返回17
1、换路后电路的微分方程
S在1位置
1
i
S
解：
R1 iC
+
－US
C
iL
L
uC
R2
∵t = 0－，电路稳态 uL C 开路，L短路,
iL(0－ ) =US/(R1+R2) uC(0－ )= iL(0－ ) R2
在S闭合的瞬间，根据换路定律有：
uC(0－ ) = uC(0+ ), iL(0－ ) = iL(0+ ) 所以有等效电路：
h
返回14
=C d(USe－t/RC) ／dt =－(US/R) e－t/RC uR(t) = i(t) R =－US e－t/RC
h
返回19
显然uC、i、uR 都是按同样的指数规 律变化的，且都是按指数规律衰减，最 后趋于零。
电力系统暂态分析(第四章习题答案)
za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
1) 当 za = zb = zc 时 ， 非 对 角 元 素 Z1 = za 1 + a2 +
a = Z2 = 0，则三序分量可以解藕。
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流：
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流：
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
零序电压标幺值：
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流：
0.0787 I1 = −0.12＋(−0.014)//0.244） = 0.748
0.244 I2 = I1 × （ − 0.014 + 0.244） = 0.794
I3 = I1 − I2 = −0.0455 电流有名值：
障时的正序、负序、零序等效电路； 解：正序： 负序：
零序：
电力系统暂态分析电力系统(第三版)习题解答
电力系统暂态分析(第三版） 李光琦 习题解答第一章 电力系统分析基础知识1-2-1 对例1-2，取kV 1102=B U ，MVA S B 30=,用准确和近似计算法计算参数标幺值。
解：①准确计算法：选取第二段为基本段，取kV 1102=B U ，MVA S B 30=，则其余两段的电压基准值分别为：9.5kV kV 1101215.10211=⨯==B B U k U kV 6.66.6110110223===k U U B B 电流基准值：kA U S I B B B 8.15.9330311=⨯==kA U S I B B B 16.0110330322=⨯==各元件的电抗标幺值分别为：发电机：32.05.930305.1026.0221=⨯⨯=*x 变压器1T ：222121300.1050.12111031.5x *=⨯⨯= 输电线路：079.011030804.023=⨯⨯=*x 变压器2T ：21.01103015110105.02224=⨯⨯=*x 电抗器：4.03.062.26.6605.05=⨯⨯=*x 电缆线路：14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值：16.15.911==*E ②近似算法：取MVA S B 30=，各段电压电流基准值分别为：kV U B 5.101=，kA I B 65.15.103301=⨯=kV U B 1152=，kA I B 15.01153301=⨯=kV U B 3.63=，kA I B 75.23.63301=⨯=各元件电抗标幺值：发电机：26.05.1030305.1026.0221=⨯⨯=*x 变压器1T ：11.05.3130115121105.0222=⨯⨯=*x 输电线路：073.011530804.023=⨯⨯=*x 变压器2T ：21.01530115115105.0224=⨯⨯=*x 电抗器：44.03.075.23.6605.05=⨯⨯=*x 电缆线路：151.03.6305.208.026=⨯⨯=*x电源电动势标幺值：05.15.1011==*E1-3-1 在例1-4中，若6.3kV 母线的三相电压为： )cos(3.62αω+⨯=t U s a)120cos(3.62ο-+⨯=αωt U s a)120cos(3.62ο++⨯=αωt U s a在空载情况下f 点突然三相短路，设突然三相短路时ο30=α。
3.电路的暂态分析-习题课
−t
τ
的等效电路： ★元件 L、C 的等效电路：
条 元 件 件
C Uo Uo
零初始 t = 0+
非零初始 t = 0+
直流稳态 t = 0- ，∞
+
Io L
-
+
Io
-
★初始值的确定 1)画t =0-的等效电路求 uC ( 0– ) 、iL ( 0– )； 画 等效电路求 2) 根据换路定则求出
3.画 t = ∞时的等效电路，求 f (∞)； 画 时的等效电路， 时的等效电路 4. 画 t＞0 时无源网络，求等效电阻Ro，计算 时无源网络，求等效电阻 计算τ； 计算 L 先求 R0 , τ = R0C， τ = R0 5. 代入三要素公式。 代入三要素公式。
f (t ) = f (∞) +[ f (0+ ) − f (∞)] e
第二阶段: 第二阶段 20ms ~ K R1 1k 1 2
（K由 1→2） 由 → ）
起始值 R1
i
3µ C
+ 1k R3 2k U1 _ 3V + R2 U2 _ 5V
uC
i
R3 + _ U2 R2 + _
uC
t=20 + ms 时等效电路
u C ( 20 ms
+
)
−
i ( 20 ms )
+
= u C ( 20 ms
R2 u C (∞ ) = ⋅U 1 = 2 V R1 + R 2
第一阶段（ ： → ） 第一阶段（K：3→1） 时间常数
3
1 +
K R1 1k
i
2k 3µ 3V R2 C来自uCR1 +i
第3章 电路的暂态分析-答案.
第3章 电路的暂态分析练习与思考3.1.1 什么是稳态？什么是暂态？答：稳态是指电路长时间工作于某一状态，电流、电压为一稳定值。
暂态是指电路从一种稳态向另一种稳态转变的过渡过程。
3.1.2 在图3-3所示电路中，当开关S 闭合后，是否会产生暂态过程？为什么？图3-3 练习与思考3.1.2图答：不会产生暂态过程。
因为电阻是一个暂态元件，其瞬间响应仅与瞬间激励有关，与以前的状态无关，所以开关S 闭合后，电路不会产生暂态过程。
3.1.3 为什么白炽灯接入电源后会立即发光，而日光灯接入电源后要经过一段时间才发光？答：白炽灯是电阻性负载，电阻是一个暂态元件，其暂态响应仅与暂态的激励有关，与以前的状态无关；而日光灯是一个电感性负载，电感是一个记忆元件，暂态响应不仅与暂态激励有关，还与电感元件以前的工作状态有关，能量不能发生突变，所以日光灯要经过一段时间才发光。
3.2.1任何电路在换路时是否都会产生暂态过程？电路产生暂态的条件是什么？答：不是。
只有含有储能元件即电容或电感的电路，在换路时才会产生暂态过程。
电路产生暂态的条件是电路中含有储能元件，并且电路发生换路。
3.2.2若一个电感元件两端电压为零，其储能是否一定为零？若一个电容元件中的电流为零，其储能是否一定为零？为什么？答：若一个电感元件两端电压为零，其储能不一定为零，因为电感元件电压为零，由dt di Lu =只能说明电流的变化率为零，实际电流可能不为零，由221Li W L =知电感储能不为零。
若一个电容元件中的电流为零，其储能不一定为零，因为电容元件电流为零，由dt du Ci =只能说明电压变化率为零，实际电压可能不为零，由221)(Cu t W C =知电容储能不为零。
3.2.3在含有储能元件的电路中，电容和电感什么时候可视为开路？什么时候可视为短路？答：电路达到稳定状态时，电容电压和电感电流为恒定不变的值时，电容可视为开路，电感可视为短路。
3.2.4 在图3-13所示电路中，白炽灯分别和R 、L 、C 串联。
电力系统暂态分析知识讲解
电力系统暂态一、判断题1、分析电力系统并列运行稳定性时，不必考虑负序电流分量的影响。
（√）2、短路电流在最恶劣短路情况下的最大瞬时值称为短路冲击电流。
（√）3、不对称短路时，短路点负序电压最高，发电机机端正序电压最高。
（√）4、由于电力系统中三序分量是相互独立的，所以可以分别计算，然后再将各序分量迭加得到各相的电流和电压。
“√”5、快速切除故障有利于改善简单电力系统的暂态稳定性。
“√”6、中性点不接地系统中发生两相短路接地时流过故障相的电流与同一地点发生两相短路时流过故障相的电流大小相等。
“√”7、电力系统横向故障指各种类型的短路故障“√”8、运算曲线的编制过程中已近似考虑了负荷对短路电流的影响，所以在应用运算曲线法计算短路电流时，可以不再考虑负荷的影响。
“√”9、从严格的意义上讲，电力系统总是处于暂态过程之中。
（√）10、不管同步发电机的类型如何，定子绕组与转子绕组之间互感系数都是变化的。
（√）11、对称分量法只能用于线性电力系统不对称故障的分析计算。
（√）12、派克变换前后，发电机气隙中的磁场保持不变。
（√）13、同步发电机转子的惯性时间常数J T反映了转子惯性的大小。
（√）14、短路计算时的计算电抗是以发电机的额定容量为基准的电抗标幺值。
（√）15、切除部分负荷是在电力系统静态稳定性有被破坏的危机情况下，采取的临时措施二、选择题1、近似计算法中，变压器的变比应采用（C ）。
A、实际变比；B、额定变比；C、平均额定变比。
2、电力系统一相断线时的复合序网在形式上与（B ）的复合序网相同。
A、单相接地短路；B、两相短路接地；C、两相短路。
3、电力系统的复杂故障是指（C ）。
A、横向故障；B、纵向故障；C、电力系统中不同地点同时发生不对称故障。
4、如三相短路瞬间A相非周期电流起始值为最大值，则B、C两相非周期分量电流起始值（A ）。
A、大小相等，均等于A相非周期分量的一半；B、大小相等，均等于零；C、大小不相等。
电工技术第三章 电路的暂态分析习题解答
第三章 电路的暂态分析含有电感或电容储能元件的电路，在换路时会出现暂态过程。
本章研究了暂态过程中电压与电流的变化规律。
主要内容：1．暂态过程的基本概念。
2．换路定则：在换路瞬间，电容电流和电感电压为有限值的情况下，电容电压 和电感电流在换路前后的瞬间保持不变。
3．RC 电路的零输入响应、零状态响应和全响应。
4．RL 电路的零输入响应、零状态响应和全响应。
5．一阶线性电路暂态分析的三要素法：一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。
6．暂态过程的应用：对于RC 串联电路，当输入矩形脉冲，若适当的选择参数 和输出，可构成微分电路或积分电路。
[练习与思考]解答3-1-1什么是稳态？什么是暂态？解：当电路的结构、元件参数及激励一定时，电路的工作状态也就一定，且电流和电压为某一稳定的值，此时电路所处的工作状态就称为稳定状态，简称为稳态。
在含有储能元件的电路中，当电路的发生换路时，由于储能元件储的能量的变化，电路将从原来的稳定状态经历一定时间变换到新的稳定状态，这一变换过程称为过渡过程，电路的过渡过程通常是很短的，所以又称暂态过程。
3-1-2什么是暂态过程？产生暂态过程的原因是什么？解：含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程（过渡过程）。
暂态过程产生的内因是电路中含有储能元件，外因是电路发生换路。
3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值？解：初始值是暂态过程的+=0t 时刻的值，稳态值是暂态过程的∞=t 时刻的值。
3-2-2 如何求暂态过程的初始值？解：求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路，求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。
对直流电路，如果换路前电路处于稳态，则电容相当于开路，电感相当于短路。
电子电工学第2章电路的暂态分析的教案
微分方程式：
L R
d iL dt
iL
IS
US
S
最后求得：
Rt
t
iL IS(1 e L ) IS(1 e τ )
uL
L d iL dt
t
RIS e
t
US e
时间常数:
L
R
R
iL
uL
返回
上一节
下一节
上一页
下一页
第2章 电路的暂态分析
(三) RL 电路的全响应 a
S
R
b
iL
U0
US
直流电路中 U = 常数
I =0 C 相当于开路,隔直流作用
返回
上一节
下一节
上一页
下一页
电容串联
u1
u
u2
1 1 1 C C1 C2
u1
C2 C1 C2
u
u2
C1 C1 C2
u
第2章 电路的暂态分析
电容并联
C1 C2
u
C1 C2
C C1 C2
上一节
下一节
上一页
第2章 电路的暂态分析
(二) 电感
t
e
R
t
(IS I0)e
返回
上一节
下一节
上一页
下一页
第2章 电路的暂态分析
uC、iC 变化规律与 U0 和 US 相对大小有关。
O
O
返回
上一节
下一节
上一页
下一页
第2章 电路的暂态分析
2.4 RL电路的暂态分析
(一) RL 电路的零输入响应
t = 0 时换路
换路前,S 合在a端
第2章电路的暂态分析习题答案
+
IS
u(t)
R1
−
S
t=0
C
R2
题图 2.7
2
e4 )
=
22(1 −
e−7.5 )
= 22 (1 − 0.000553 ) = 21 .9878 A
− 15 ×2
i2 = 5.5e 4 = 5.5 × 0.000553 = 0.00304 A
第二个暂态 i1(0 + ) = i1(0− ) = 21 .9878 ≈ 22 A i2 (0 + ) = −i1 (0 + ) = −22 A
第 2 章 电路的暂态分析
学 习 目标
了解电路产生过渡过程的原因和研究过渡过程的意义。 掌握换路定律及电路初始值、稳态值的计算方法。 理解电路中激励和响应的概念，理解时间常数的物理意义。 了解一阶 RC 电路零输入响应、零状态响应和全响应的物理意义和一般求 法。 了解微分电路、积分电路的电路形式、条件和电压波形。 了解一阶 RL 电路零输入响应、零状态响应和全响应的一般分析方法。 掌握利用三要素法分析一阶 RC、RL 电路过渡过程的方法。
t1 = 5 × 0.693 = 3.475 S (4) i (3τ ) = 9 × 10 −5 × e −3τ /τ = 9 × 10 −5 × e −3 = 4 .48 μA i(5τ ) = 9 × 10 −5 × e −5 = 0 .6 μA 可以看出经过 5τ后，暂态过程基本结束。
暂态分析习题答案
暂态分析习题答案暂态分析习题答案是电力系统分析中的重要部分，它可以帮助我们了解电力系统在瞬态过程中的动态响应和稳定性。
在这篇文章中，我们将探讨几个常见的暂态分析习题，并给出详细的解答。
第一个习题是关于电力系统中的短路故障。
假设一个三相电力系统中发生了一次对地短路故障，故障电流为1000A，故障持续时间为0.1秒。
系统的额定电压为10kV，发电机的暂态电抗为0.2，负载的暂态电抗为0.1。
求故障后系统的电压和电流。
首先，我们需要计算故障电流的幅值。
由于故障电流为对地短路，其幅值为故障电流的三相幅值的1/√3倍。
因此，故障电流的幅值为1000A/√3 ≈ 577A。
接下来，我们可以使用短路电流计算方法来计算故障后的电压和电流。
根据短路电流计算方法，故障后的电压可以表示为：Uf = U0 - Zf * If其中，Uf为故障后的电压，U0为额定电压，Zf为系统的暂态阻抗，If为故障电流。
代入数值计算，我们得到：Uf = 10kV - (0.2 + 0.1j) * 577A ≈ 10kV - 115.4kVA ≈ 9.884kV因此，故障后系统的电压约为9.884kV。
接下来，我们可以使用功率方程来计算故障后的电流。
根据功率方程，故障后的电流可以表示为：If = (U0 - Uf) / Zf代入数值计算，我们得到：If = (10kV - 9.884kV) / (0.2 + 0.1j) ≈ 116.4A因此，故障后系统的电流约为116.4A。
第二个习题是关于电力系统中的过电压问题。
假设一个三相电力系统中，当一台发电机突然失去负载时，系统的电压会出现过电压现象。
假设系统的额定电压为10kV，发电机的暂态电抗为0.2，负载的暂态电抗为0.1。
求失去负载后系统的电压。
在失去负载时，发电机的电压会突然升高。
根据过电压计算方法，失去负载后的电压可以表示为：Uf = U0 + Zg * Ig其中，Uf为失去负载后的电压，U0为额定电压，Zg为发电机的暂态阻抗，Ig为发电机的电流。
2010年暂态习题课
暂态第2章2-1 什么是Park 变换？答：把原来定子a ，b ，c 三相参数变换到定子d ，q ，零轴的坐标变换方法称之为park 变换。
它是使描述各量的参数在两个不同的坐标系下转换。
正变换矩阵：abc->dq0，()()()()0c o s c o s 120c o s 1202s in s in 120s in 1203111222d q a b c ooooA P A P θθθθθθ=⎡⎤-+⎢⎥⎢⎥=⎢----+⎥⎢⎥⎢⎥⎢⎥⎣⎦反变换矩阵：dq0-> abc ，()()()()11c o s s in 1c o s 120s in 1201c o s 120s in 1201a b c d q ooo oA PA Pθθθθθθ--=⎡⎤-⎢⎥⎢⎥=---⎢⎥⎢⎥+-+⎣⎦2-2 写出同步发电机定子、转子绕组正电流产生正磁链的有阻尼绕组发电机d 、q 、0系统的磁链方程。
2-3 请给出同步发电机的各种电抗参数的等值电路和表达式，并排出大小顺序。
d x ，q x ，dx '，d x ''，q x ''，f x ，D x ，Q x 答：d a d x x x σ=+，q a q x x x σ=+，1//11da d f a df x x x x x x x σσσσ'=+=++，1////111da d f D a df D x x x x x x x xx σσσσσσ''=+=+++，1//11qa q Q a qQ x x x x x x x σσσσ''=+=++，f f a dx x x σ=+，D D adx x x σ=+，Q Q a qx x x σ=+2-4 请给出同步发电机的各种电势的等值电路、表达式及相量图。
q E ，Q E ，E '，qE '，E ''，qE ''，d E ''答：qdd E Ur Ij x Ij x I =+++ ，Q qE U rI jx I =++ ，dE U jIx ''=+&&，q q ddE U jI x ''=+&&，q ddE U jI x ''''=+&&，q q ddE U jI x ''''=+&&，d d q qE U jI x ''''=+&&，q q d dU E jI x =-&&&，d q q U jI x =-&&2-5 试写出同步发电机（隐极机和凸极机）稳态运行时的基本方程，并画出等值电路和相量图。
第三章 电路暂态分析 习题课
返 回练习题题集
上一页
下一题
7在图所示电路中，开关 S 闭合前电路已处于稳态，试确 定 S 闭合后电压 uL 和电流 iL、i1、 i2 的初始值和稳态值。
L
iL
+ uL + U S 12 V -
i1
4Ω
S
i2
R1
R2
6Ω
【解】 (1)求初始值 由于 S 闭合前，电路已稳定， L 相当于短路，R2 两端的电压等于 US， R2 中的电流即 iL。因 此，根据换路定律，由换路前( S 断开时)的电路，首先求得
第三章 电路暂态分析
1、已知： S 在“1”处已 经达到稳态，在t=0时合
S
2 R 1 + _ E =6V 2k
i
i1
R1
i2
2k
R2 1k
向“2”
求:
i、i1、i 2 u C 、uL
的初始值。
-
uL
uC
解：
换路前即 t = 0 时的等效电路
+ E _ i1 R R1 R2
uC
E = 1.5mA i 1(0 ) = R +R 1
(2) 在(1)中, 若使uRL不超过220V, _ 则泄放电阻R´应选多大？
U R´ L
(3) 根据(2)中所选用的电阻R´, 试求开关接通R´后经 过多长时间，线圈才能将所储的磁能放出95%？ (4) 写出(3) 中uRL随时间变化的表示式。 解: 换路前，线圈中的电流为
(1) 开关接通R´瞬间线圈两端的电压为
uL () = 0
然后，进一步求得
U S - uL ( ) 12 - 0 i1 ( ) = = A= 3A R1 4 U S - uL ( ) 12 - 0 i2 ( ) = = A=2A R2 6 i L ( ) = i1 ( ) + i2 ( ) = ( 3 + 2) A = 5 A
暂态分析习题课.doc
第一章7•供电系统如图所示，各元件参数如下：线路I,50km, X尸0・4Q/km；变压器T,S/v=10MVA, u%=10.5, K T=H0/ll,假定供电点⑸ 电压为106.5kV保持恒定不变，当空载运行时变压器低压母线发生三相短路时，试计算：短路电流周期分量起始值、冲击电流、短路电流最大有效值及短路容量的有名值。
解：设基准容量S尸10MVA错误!未找到引用源。
，釆用平均电压近似计算法。
各元件的标么值求得如下：供电点发电机：线路L:变压器T:X* = 0.105则计算可得短路电流有效值的标么值:则算得短路电流的有效值的有名值:Sa 10心屁7 二7.710* L =4.24KA如10.5最大值即为短路电流周期分量起始值：/,… = V2/z =血*4.24 = 5.996KA冲击电流为：i M = I m =1.8*5.995 = 10.792AL4取错误!未找到引用源。
，则短路电流最大有效值电流为: + 2（心-1尸二4*1.52二6・445恥V2106.5115=0.92610I151-0.01510.926 一“0.0151 +0.105 = 7710—50* 0.4*5 V短路容量有名值为：Sd= -5u av l d = 1.732 *10.5* 4.24 = 1JAMVA或者：S d = I 幽勿=7.71 水 10 = 77.1MVA8.教材 P161-3-1解： （1） U,n = V2x6.3（2）取T a = 0.0055 ,短路前为空载 所以,Z -|o| = °X （p = arctg —= r 因为 所以,i a = I m sin （M + a-（p ）-I fn sin （o - 仞厂心005= 9.448 sin （ax + 62.36°） - 8.370^/0005 i h = I m sin© + a -120° - 卩）一 l m sin （a 一 120° -（p ）e't,Q ^5 = 9.448 sin （血一 57.64°） + 7.981 严曲 i c = I m sin （曲 + a +120° - 卩）- I m sin （a +120° -（p ）eT m = 9.448sin 伽-182.36°） + O.389^r/0005（3）三相直流分量幅值分别为，-二8.370kV,泸7・981kV,j=0・389kV 。
电路的暂态分析习题解答
第五章 电路的暂态分析5.1 题5.1图所示各电路在换路前都处于稳态，求换路后电流i 的初始值和稳态值。
解：（a ）A i i L L 326)0()0(===-+，换路后瞬间 A i i L 5.1)0(21)0(==++ 稳态时，电感电压为0， A i 326==（b ）V u u C C 6)0()0(==-+， 换路后瞬间 02)0(6)0(=-=++C u i 稳态时，电容电流为0， A i 5.1226=+=（c ）A i i L L 6)0()0(11==-+，0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路，故 0=i（d ）2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+(a)(b)(d)(c)CC2Ω2+6V -题5.1图i稳态时电容相当于开路，故 A i 12226=++=5.2 题5.2图所示电路中，S 闭合前电路处于稳态，求u L 、i C 和i R 的初始值。
解：换路后瞬间 (0)6L i A +=，(0)3618C u V +=⨯= (0)6(0)0R L i i ++=-=(0)18(0)(0)6033C C L u i i +++=-=-=(0)(0)(0)0L C R u u Ri ++++==，(0)(0)18L C u u V ++=-=-5.3 求题5.3图所示电路换路后u L 和i C 的初始值。
设换路前电路已处于稳态。
解：换路后，(0)(0)4L L i i mA +-==，所以换路后4mA 电流全部流过R 2，即(0)4C i mA +=由于(0)(0)8C C u u V +-==，故2(0)(1)(0)(0)20812L L c u R R i u V+++=-++=-+=-5.4 题5.4图所示电路中，换路前电路已处于稳态，求换路后的i 、i L 和 u L 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章7.供电系统如图所示，各元件参数如下：线路l ，50km ，X 1=0.4Ω/km ；变压器T ,S N =10MV A ，u%=10.5，K T =110/11，假定供电点(S )电压为106.5kV 保持恒定不变，当空载运行时变压器低压母线发生三相短路时，试计算：短路电流周期分量起始值、冲击电流、短路电流最大有效值及短路容量的有名值。
解：设基准容量S B =10MV A 错误！未找到引用源。
,采用平均电压近似计算法。
各元件的标么值求得如下： 供电点发电机：线路L:变压器T:则计算可得短路电流有效值的标么值:则算得短路电流的有效值的有名值:*107.710* 4.2433*10.5B d d B S I I KA U === 最大值即为短路电流周期分量起始值：22*4.24 5.996m d I I KA === 冲击电流为：1.8*5.99510.792M M m i K I KA ===取错误！未找到引用源。
，则短路电流最大有效值电流为:212(1)*1.52 6.44522m m M M I I I K KA =+-==短路容量有名值为:3 1.732*10.5*4.2477.1d av d S U I MVA === 或者：8. 教材P16 1-3-1 解：(1) 3.62⨯=m U 2 6.39.4480.943m U m zI K A ⨯===(2) 取s T a 005.0=， 短路前为空载 所以，00=m I064.57505.0797.0===arctg r x arctg ϕ 因为0090120a α=+=所以，/0.005sin()sin()t a m m i I t a I a e ωϕϕ-=+---0/0.0059.448sin(62.36)8.370t t e ω-=+-00/0.0050/0.005sin(120)sin(120)9.448sin(57.64)7.981t t b m m i I t a I a e t e ωϕϕω--=+-----=-+00/0.0050/0.005sin(120)sin(120)9.448sin(182.36)0.389t t c m m i I t a I a e t e ωϕϕω--=++--+-=-+(3) 三相直流分量幅值分别为，a i =8.370kV , b i =7.981 kV ,c i =0.389 kV 。
所以，a 相瞬时电流最大(4) 90a ϕ-=时，最大瞬时电流为冲击电流090147.64α+=或09032.36α+=- 则57.64α=或122.36α=- 9. 教材P16 1-3-2 解：02180/10000.255m I kA =⨯=00sin()sin()a m m C I a I a ϕϕ=---0.255s i n (12030)9.448s i n (1=-8.115k A=⨯--00sin(120)sin(120)b m m C I a I a ϕϕ=-----0.255s i n (12012030)9.448s i n (120)=7.853k A=⨯---00sin(120)sin(120)c m m C I a I a ϕϕ=+--+-0.255s i n (12012030)9.448s i n (120)=0.262k A=⨯+--10.(1) 若短路前空载，计算短路电流的周期分量及短路电流最大有效值； (2) 若A 相非周期分量电流的初值为零及最大时，计算相应的B 、C 相非周期分量电流的初始值；解：（1）设基准容量S B =10MV A 错误！未找到引用源。
，采用平均电压近似计算法。
各元件的标么值求得如下： 供电点发电机：*1151115E ==线路L:变压器T:则计算可得短路电流有效值的标么值:***18.32640.01510.105d E I X ===∑+则算得短路电流的有效值的有名值:*108.3264* 4.57833*10.5B d d B S I I KA U === 最大值即为短路电流周期分量起始值：22*4.578 6.475m d I I KA ===所以：sin()0.59sin()pa m i I t t ωαϕωαϕ=+-=+- 取错误！未找到引用源。
，则短路电流最大有效值电流为:212(1)*1.52 6.95922m m M M I I I K KA =+-==（2）：A 相非周期分量电流初始值：()()()()0|0||0|sin sin sin 6.475sin a m m m i I I I ααϕαϕαϕαϕ=---=--=--若︒=-⇒=000ϕααa i ，则：()()00sin 120 5.608sin 120 5.608b m c m i I kA i I kAαα︒︒=--==-=-若︒-=-⇒=900ϕααMAX i a ，则：()()000 6.475sin 12090 3.238sin 12090 3.238a m b m c m i I kAi I kA i I kA ααα︒︒︒︒===---=-=--=- 解： 归算在高压侧的参数：Ω=⨯=Ω=⨯=05.127101101005.1020504.02T l X X 归算到短路点所在电压等级（低压侧）的参数为：Ω=⎪⎭⎫⎝⎛⨯=∑47.11101105.1472X① 短路电流周期分量：()()()|0|2sin sin 336.388sin m pa U U i t t X X t ωαφωαφωαφ∑∑=+-=+-=+-短路电流最大有效值：kA I I m M 863.62388.652.1252.1=⨯=⨯= ②A 相非周期分量电流初始值：()()()()ϕαϕαϕαϕαα--=--=---=sin 388.6sin sin sin |0||0|0m m m a I I I i若︒=-⇒=000ϕααa i ，则：()()kAI i kA I i Mc M b 53.5120sin 53.5120sin 00-=-==--=︒︒αα 若︒-=-⇒=900ϕααMAX i a ，则：()()kAI i kA I i kA I i Mc M b M a 194..390120sin 194.390120sin 388.6000-=--=-=---===︒︒︒︒ααα第二章5. 已知同步发电机的参数为：x d =1.2，x q =0.8，x d ’=0.29，x d ’’=0.25，x q ’’=0.35。
发电机在额定运行时，U =1，I =1，错误！未找到引用源。
试计算额定运行状态下同步发电机的E Q 、E q 、E q ’、E q ’’、E d ’’和E ’’的值。
解：cos 0.8ϕ=； 036.87ϕ= 1=∙U0136.870.80.6I j ∙=∠-=-0385.2361245.164.048.1)6.08.0(8.01∠=+=-+=+=∙∙∙i j j X I j U E q Q0385.23=δ)(q d d Q q x x I j E E -+=∙∙∙=1.61245sin()(1.20.8) 1.61245sin(23.38536.87)0.4I δϕ++-=++⨯=1.9597cos cos 23.3850.868240.29 1.1696q q d d d d E U I x u I x δ'''=+=+=+⨯= cos 23.3850.868240.25 1.13492q q d d E U I x ''''=+=+⨯=sin 23.385cos(23.38536.87)0.350.22325d q q q U x E I ''''==-+⨯-=22()() 1.15667q d E E E ''''''=+=6. 一台有阻尼同步发电机，已知：P N =200MW ，错误！未找到引用源。
，U N =15.75KV ，x d = x q =0.962，x d ’=0.246，x d ’’=0.146，x q ’’=0.21。
发电机在额定电压下运行，带负荷(180+j110)MV .A ，机端突然发生3相短路，试求： (1) E q 、E q ’、E q ’’、E d ’’和E ’’在短路前瞬间和短路后瞬间的值。
(2) 起始次暂态电流。
解：1）200,cos 0.85N N P MW ϕ==200235.294()cos 0.85N N N P S MVA ϕ===180110;S j =+ 0110()31.43180arctg ϕ== 00*210.9531.430.896531.43235.294S ∠==∠2008.6252()315.750.85N I KA ==⨯⨯210.957.733()3315.75N S I KA U ===⨯ 043.31897.06252.8733.7-∠==∙I 031.43ϕ= 0010.89731.430.96210.86299031.43q Q d E U j I x j ∙∙∙=+=+∠-⋅=+∠-=1.450.7363 1.626226.92o j +=∠ 026.92δ=() 1.6262q Q d d q q E E I x x E =+-== （有名值 25.61KV ）cos cos 26.920.8970.246sin(26.9231.43)q q d d d d E U I x u I x δ'''=+=+=+⨯⨯+=1.07948 （有名值 17KV ）cos 26.920.8970.146sin(26.9231.43)q q d d E U I x ''''=+=+⨯⨯+=1.0031234 （有名值5.574KV ）sin 26.920.8970.21cos(26.9231.43)0.3539d q q q E U I x ''''=-=-⨯⨯+=（有名值5.574KV ）22()() 1.0637q dE E E ''''''=+= （有名值 16.75KV ） 短路后瞬间：q E ''、d E ''、E ''、'q E 保持不变，q E 发生变化 用公式 q q d dE U I x =+ q q d d E U I x ''=+因为 0q U = ，所以 q d d E I x ''= 而短路瞬间的 1.00312346.687070.146q d d E I x ''''===''6.87070.9626.q E =⨯= （有名值104.1KV ）2）0.3539 1.68520.21d q q E I x ''''===''有： 22()()7.0743q d I I I ''''''=+=有名值为 7.07430.62526I ''=⨯=（KA ）9. 同步发电机参数：x d =1.2，x q =0.8，x d ’=0.35，x d ’’=0.2，x q ’’=0.25，变压器参数XT=0.15，运行状态为高压侧U =1，I =1，错误！未找到引用源。