深度迭代和参数颜色功能
几何画板制作深度迭代的方法探究

对应规则:A→A'。
6、选中参数用加减键调整参数,可得到变化的多边形。
7、对参数创建“动画”。
温馨提示:最好在制作之前将精确度精确到个位。
最后制作的效果图:
二、正方形深度迭代
先看最终效果图,如何制作呢?
制作方法:
1、构造正方形、确定原象:
从左至右画线段AB(A、B即为原象);
双击A点→选中AB→变换→旋转→逆时针旋转90°→得C;
双击C点→选中CA→变换→旋转→逆时针旋转90°→得D;
连续BD。
2、构造初象:
在线段AB上任取一点E(其中一个初象),按顺序选中A、B、E→度量→比→标记比;
双击B→将D按标记比进行缩放得另一初象F。
3、新建参数:n=25;
制作方法:
1、构造下图:
构造线段AB→以B为中心将A顺时针旋转90°得点C→以C为中心将B顺时针旋转90°得点D,连结BC、CD、DA得正方形ABCD。
2、以O为中心,分别将E、F、G、H按1:2的缩放比缩放得E’、F’、G’、H’,连结EE’、FF’、GG’、HH’和E’F’G’H’。
3、新建参数n=2
3、构造初象:
选中DC→按ctrl+M得DC的中点E→顺次选定E、C、D→构造→圆上的弧→在弧上构造点
F,连结DF、CF→隐藏弧。
4、新建参数n=3
5、深度迭代:
选中原象A、B和参数→变换→按住shift键→深度迭代;
对应规则:A对D,B对F;(新添映射)A对F,B对C。
6、设置F的“动画”;
7、系列按钮的创建:
4、深度迭代:选定A、B和n,按如下方式进行深度迭代。(注意:在下图显示中一定要选“最终迭代”)
勾股树
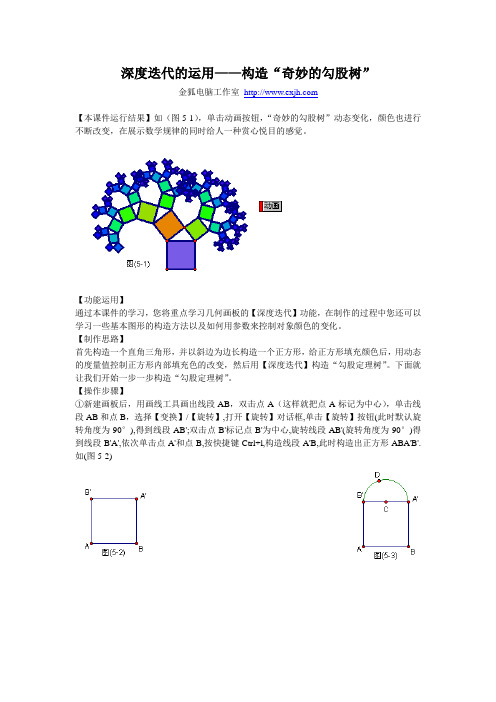
深度迭代的运用——构造“奇妙的勾股树”金狐电脑工作室【本课件运行结果】如(图5-1),单击动画按钮,“奇妙的勾股树”动态变化,颜色也进行不断改变,在展示数学规律的同时给人一种赏心悦目的感觉。
【功能运用】通过本课件的学习,您将重点学习几何画板的【深度迭代】功能,在制作的过程中您还可以学习一些基本图形的构造方法以及如何用参数来控制对象颜色的变化。
【制作思路】首先构造一个直角三角形,并以斜边为边长构造一个正方形,给正方形填充颜色后,用动态的度量值控制正方形内部填充色的改变,然后用【深度迭代】构造“勾股定理树”。
下面就让我们开始一步一步构造“勾股定理树”。
【操作步骤】①新建画板后,用画线工具画出线段AB,双击点A(这样就把点A标记为中心),单击线段AB和点B,选择【变换】/【旋转】,打开【旋转】对话框,单击【旋转】按钮(此时默认旋转角度为90°),得到线段AB';双击点B'标记点B'为中心,旋转线段AB'(旋转角度为90°)得到线段B'A',依次单击点A'和点B,按快捷键Ctrl+l,构造线段A'B,此时构造出正方形ABA'B'.如(图5-2)②单击选中线段A'B',按Ctrl+M 组合键,构造出A'B'的中点C(点C 为选中状态),再依次选中点A'和B'(注意顺序不要搞错啊),选择【构造】/【圆上的弧】,构造出以A'B'为直径的半圆,用画点工具在半圆上画出点D.如图(5-3)③依次单击选中点A 、B 、A'、B',选择【构造】/【四边形内部】,把正方形填充上颜色;在工作区空白处单击后单击选中点A 、D ,选择【度量】/【距离】得到A 、D 两点间的度量值。
如(图5-4)④依次单击选中正方形的填充色和度量值,选择【显示】/【颜色】/【参数】打开【颜色参数】对话框,按图(5-5)进行设置.(用鼠标托动点D 看看正方形的填充色有什么改变么)(图5-5)(图5-6)⑤选择【图表】/【新建参数】打开【新建参数】对话框,如(图5-6),单击【确定】得到参数t 1=1.⑥依次选中半圆和点C,按组合键Ctrl+H(隐藏它们,为了后面观察方便);依次单击选中点A 、点B 、参数t 1=1.0,按住Shfit 键的同时选择【变换】/【深度迭代】弹出【深度迭代】对话框,如(图5-7)。
利用几何画板制作数学课件(六)

• 单击工作区的计算值a2=4,来映射 a a2, 工作区显示如(图2);
• (3)单击【迭代】按钮后,最后效果参数a 的值,初象a2 的值相应改 变,如(图4);
• 选中迭代产生的表格,按小键盘上的“+” 号键可以 • 增加迭代的次数,如(图5),按“-”键 则减少迭代的次数。
• (5) 依次选中参数a 和b, 从【变换】菜 单选择【迭代】命令,打开迭代对话框, 如(图18);
• (6) 在对话框中,a 映射的初象反白显示 时,单击工作区中的a+1 的计算值;b 映射 的初象反白时,单击工作区中b+2 的计算 值。工作区如(图19);
• (7)单击迭代完成,最后效果如(图20)。
• 4.新建参数n=4,顺次选择A、B两点和参 数n,作深度迭代,(A,B)(G,P); (P,O);(O,J);(F,M);(M, N);(N,K);(A,E);(E,L); (L,B)。注意迭代中点的对应,当迭代 框遮住图像的时候可用鼠标选中拖动开。 单击迭代,隐藏不必要的点。
• (2)依次单击a+1 和b+2 两个计算值, 选择【图表】菜单下的【绘制(x,y)】 命令,如(图15);
• (3)单击该命令后系统自动调出坐标系, 并绘制出以所选计算值为坐标的点,如 (图16);
• (4)用同样方法绘制出以参数a、b 为坐标 的点, 选中绘制的两个点构造线段,如 (图17);
• 【例6】画圆的内接正7边形。 • 【分析】由正7边形的特征,我们知道,每一个点 都相当于前面的点逆时针旋转,抓住这个规律, 我们可以用迭代功能来解决。 • 【步骤】 • 1.新建圆O,在圆O上任取一点A。 • 2.双击圆心O作为旋转中心。选中A点,单击菜单 【变换】【缩放】,旋转参数选为选择固定角度, 然后在框中输入360/7,得到B点。连接线段AB。
encoderparameters详解

encoderparameters详解EncoderParameters是一个用于设置图像编码器参数的类。
在图像处理中,编码器是用于将图像数据转换为特定格式的工具。
EncoderParameters类提供了一种灵活的方式来设置编码器的参数,以便在图像编码过程中进行各种调整和优化。
EncoderParameters类包含一个名为Param的属性,它是一个EncoderParameter数组。
EncoderParameter类用于表示编码器的参数。
每个EncoderParameter对象包含一个名为Encoder的属性,用于指定编码器的类型,以及一个名为Value的属性,用于指定参数的值。
使用EncoderParameters类可以实现许多图像编码的高级功能。
例如,可以使用EncoderParameters类来设置图像的压缩质量、颜色深度、图像格式等。
下面将详细介绍一些常用的EncoderParameters参数。
1. 压缩质量参数(Encoder.Quality)压缩质量参数用于指定图像的压缩质量级别。
它的值范围从0到100,其中0表示最低质量,100表示最高质量。
通过调整压缩质量参数,可以在图像质量和文件大小之间进行平衡。
2. 颜色深度参数(Encoder.ColorDepth)颜色深度参数用于指定图像的颜色深度。
它的值通常为8、16、24或32,表示每个像素使用的位数。
较高的颜色深度可以提供更丰富的颜色表现,但也会增加文件大小。
3. 图像格式参数(Encoder.ImageFormat)图像格式参数用于指定图像的输出格式。
常见的图像格式包括JPEG、PNG、BMP等。
通过设置图像格式参数,可以将图像保存为不同的文件格式。
除了上述常用的参数外,EncoderParameters还支持许多其他参数,如图像的DPI(每英寸点数)、图像的压缩方式、图像的调色板等。
通过灵活使用EncoderParameters类,可以根据具体需求对图像进行精确的编码控制。
几何画板在数学中应用

几何画板在数学中的学习、教学中的应用重庆市第九十五中学梁勇一、几何画板简介在21世纪,以计算机多媒体和互联网为代表的信息技术已迅速而深刻地改变着人们的工作方式、交往方式、生活方式和思维方式,信息技术正在改变传统的教学内容、教学方式、教学模式与教学观念。
在数学教学中,从课堂教学到课外辅导,从组织练习到成绩的统计评估,从教师备课、同行交流到学生课内外活动的组织,信息技术在推动数学教学改革方面都有着巨大潜力。
《几何画板》就是一个能让老师和学生操作的优秀学科软件,在动态的操作过程中,给学生的比较和抽象活动创造了一种活动的空间和条件。
学生能在活动中理解和掌握抽象的概念。
这样学生获得的才是真正的数学经验,而不只是数学结论。
既然《几何画板》有这样强大的作用,下面我和大家一起分享《几何画板》以及它在数学制卷、教学、命题、解题中的应用。
1、《几何画板》简介《几何画板》软件是由美国Key Curriculum Press公司制作并出版的几何软件,它的全名是《几何画板--21世纪的动态几何》。
《几何画板》是一个适用于几何(平面几何、解析几何、射影几何等)教学的软件平台。
它为老师和学生提供了一个探索几何图形内在关系的环境。
它以点、线、圆为基本元素,通过对这些基本元素的变换、构造、计算、动画、跟踪轨迹等,能显示或构造出其它较为复杂的图形。
2、《几何画板》的基本功能(1)作图《几何画板》在图形绘制上比一般的绘图软件更为精准,更符合数学的严格要求。
我们可以使用工具栏的画点工具、画圆工具、画线工具(线段、射线、直线),作出基本的数学图形。
(2)文字在《几何画板》中可以对各种量进行文本标记和解释,例如对点、线元素的自动习惯性标记,便于在教学过程中的理解。
(3)构造要画某线段的中点,绘制某线的平行线、垂直线等具有一定几何关系的常用图形,可以直接选中所需图形再选择“构造”菜单的相应工具即可构造出来。
(4)变换使用《几何画板》中的“变换”菜单,可按指定值、计算值或动态值任意旋转、平移、缩放原有图形,并在其变化中保持几何关系不变,从而方便我们研究图形的运动和变换等问题。
从矩形网格的制作谈几何画板的迭代深度与应用技巧

鄞州区钟公庙中学
从理论上讲,矩形网格可按如下方法制作: 在平面上任意画一个自由点 A,按给定的小矩形边长作矩形 ABCD,选定点 A 和参数 n=6,作带参 数迭代,让 A B,添加迭代 A C,再添加迭代 A D,如图 1 所示,制作完成。
注:几何画板版本不同,迭代的深度也各不相同。
4
图 15
3
图 16
上述 3 个 2 次映象,迭代深度可先预设为 n/3,经过测试当 n=7 时迭代深度还欠 1 次,修正为 round((n+1)/3)后,对于 n≤30 时都正确。 如图 16 所示是当 n=30 时图象,可以看出此时线条已十分稠密,再增加边数时图象变化已不十分明 显。 还有一种一劳永逸的方法是,作参数 n=80, 计算 n-1 和3600 /n,象图 10 哪样先不厌其烦地作出一 组对角线(共 79 条),然后再作单次映象的迭代,这样作出的图象对于 n≤80 都正确,但没有什么技术 含量,图 16 是 n=60 时情形,显然线段稠密,没有什么美感。
图 17
图 18
为了不致太稠密,我们把对角线换成一组平行弦,再作带参数的深度迭代 A B,如图 18 所示。可 得如图 19(平行弦间距相等)、图 20(平行弦间距不相等)所示精美图案。
图 19
Байду номын сангаас
图 20
至此,相信读者已经了解几何画板迭代运算随着映象的增加,电脑的运算量将是急剧增加,以致电 脑可能出现半死机状态,所以我们学会一些降低映象深度的方法和技巧是十分必要的,希望此文能对广 大几何画板爱好者有所帮助。
2
同样方法:当 n=48 时,如图 12 所示。
图 11
几何画板迭代全解

第二章:迭代与分形几何
分形作为现代数学的一个分支,从诞生的那天起,就有着独特的魅力。分形的特点是整体 与部分之间存在某种自相似性, 整体具有多种层次结构。 分形图片具有无可争议的美学感召力, 特别是对于从事分形研究的科学家来说。欣赏分形之美当然也要求具有一定的科学文化知识, 但相对而言,分形美是通俗易懂的。分形就在我们身边,我们身体中的血液循环管道系统、肺 脏气管分岔过程、大脑皮层、消化道小肠绒毛等等都是分形,参天大树、连绵的山脉、奔涌的 河水、漂浮的云朵等等,也都是分形。人们对这些东西太熟悉了,当然熟悉不等于真正理解。 分形的确贴近人们的生活, 因而由分形而来的分形艺术也并不遥远, 普通人也能体验分形之美。 因为分形几何的迭代的原像一般不止一个,而且均为多映射迭代,为了叙述的方便,我们 先作以下两个约定。 1.用(A,B,C)表示有顺序的三点 A、B 和 C。 2.(A,B,C)(D,E,F,),(G,H,I)表示 A 映射到 D,B 映射到 E,C 映射到 F,然后添加映射 A 映射到 G,B 映射到 H,C 映射到 I,以此类推。
例 2.1 Sierpinski 三角形
波兰著名数学家谢尔宾斯基在 1915-1916 年期间, 为实变函数理论构造了几个典型的例子, 这些怪物常称作“谢氏三角” 、 “谢氏地毯” 、 “谢氏海绵” 、 “谢氏墓垛” 。如今,几乎任何一本讲
第 8 页 共 23 页
《几何画板迭代全解》
图 1.1
图 1.2 在几何学中,迭代使一组对象产生一组新的对象。图 1.2 中 A、B、C、D、E、F、G,各点 相距 1cm,那么怎么由 A 点和 B 点得到其它各点呢?我们可以发现其中的规律就是从左到右, 每一个点相当于前面一个点向右平移了 1cm。所以我们以 A 点作为原像,B 点作为初像,迭代一 次得到 B 点,二次为 C 点,以此类推。 所以,迭代像就是迭代操作产生的象的序列,而迭代深度是指迭代的次数,迭代的终点就 是最后的那个像。那么下面我们通过例子来进一步地了解迭代以及相关的概念。 几何画板中迭代的控制方式分为两种,一种是没有参数的迭代,另一种是带参数的迭代, 后者我们称之为深度迭代。两者没有本质的不同,但前者需要手动改变迭代的深度,后者可通 过修改参数的值来改变迭代深度。我们先通过画圆的正 n 边形这个例子来看一下它们的区别。
几何画板中的迭代和带参数的迭代实验报告:圆的面积公式转化

几何画板中的迭代和带参数的迭代实验报告一、实验目的1、新建参数以及参数动画按钮的制作2、掌握带参数的迭代思想和操作步骤3、学会通过了解父对象和子对象的关系来逆向分析已有的几何画板课件二、实验原理通过带参数的迭代建立参数与图形之间的关系。
制作参数动画按钮时,参数的变化引起图形个数的变化。
三、实验内容运用几何画板逆向分析圆的面积公式推导课件,并将课件还原制作出来。
四、实验课时:8课时五、实验步骤(略)一、方法:分割拼凑法、划曲为直展开法(等腰三角形)、划曲为直展开法(直角三角形)。
二、实施步骤方法一:分割拼凑法1.新建文件新建页:【文件】-【文档选项】-【增加页】-【空白页面】,命名为:圆的面积推导分割拼凑法。
2.构建参数:【数据】—【新建参数】—构建两个参数:半径r=3厘米,t1=6。
【数据】—【计算参数】—【计算2个数据:分别是2*trunc(t1) 和360度/ 2*trunc(t1) 】。
3.做圆和分割圆:选择【点工具】—在空白处做点A—(保持A为选中状态)+选中r—【构造】—【以圆心和半径作圆】—(保持圆为选中状态)【构造】—【圆上的点】(为点B)。
选中参数360度/ 2*trunc(t1) —鼠标右击—【标记角度】,【双击点A+选中点B】—【变换】—【旋转】—【确定】(得到点B’)。
依次选中点A,点B,点B’—【构造】—【圆上的弧】—(保持弧选中状态)【构造】—【弧内部】—【扇形内部】。
选中点B+选中参数2*trunc(t1)—【按住shift 键】—【变换】—【深度迭代】—【将点B迭代到点B’】—【确定】(得到一个分割好扇形的圆)。
4.做分割后的一个扇形:选中点B+选中点B’—【度量】—【距离】—(保持参数选中状态)鼠标右击【标记距离】。
选择【点工具】—在空白处作点C—【变换】—【平移】(按标记距离平移,得到点C’)。
选中点C和点C’+选中参数r —【构造】—【以圆心和半径作圆】—取两圆上面交点D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迭代功能
迭代功能 迭代的两种方式:先绘制出一个“循环节”的图形(亦称原像 亦称原像)。 迭代的两种方式:先绘制出一个“循环节”的图形 亦称原像 。 1) 简单迭代 : 先选中原像一个点或多个点 , 然后执行 〈 变换 迭代 〉 命令 , 在 迭代〉 ) 简单迭代: 先选中原像一个点或多个点, 然后执行〈 变换/迭代 命令, 迭代”对话框中选取与原像点相对应的一组(初像点) “迭代”对话框中选取与原像点相对应的一组(初像点)或多组映射点和迭代次 最后按“迭代”按钮。即可得到固定迭代的像。 数,最后按“迭代”按钮。即可得到固定迭代的像。 2)深度迭代:新建一个参数 (取正整数),先选中原像一个点或多个点和参数 )深度迭代:新建一个参数n(取正整数) n,并按住 深度迭代〉 迭代” , 并按住Shift键, 然后执行 〈 变换 深度迭代 〉 命令 , 在 “ 迭代 ” 对话框中选 键 然后执行〈变换/深度迭代 命令, 取与原像点相对应的一组(初像点)或多组映射点,最后按“迭代”按钮。 取与原像点相对应的一组(初像点)或多组映射点,最后按“迭代”按钮。即可 得到动态迭代的像。选中参数n,按“ +”号键, 增加迭代,按 “-”号键,减少迭 得到动态迭代的像。 选中参数 , 号键, 增加迭代, 号键, 号键 号键 代。 原像点的确定:取决于绘制基本图形的起始条件,如用线段绘制正多边形, 原像点的确定:取决于绘制基本图形的起始条件,如用线段绘制正多边形,取第 一条边的两个端点为原像点;若用圆绘制正多边形,则取第一个顶点为原像点。 一条边的两个端点为原像点;若用圆绘制正多边形,则取第一个顶点为原像点。 动态演示 2
返回 主菜单
参数动态地改变颜色
A
B
AB = 2.96 厘厘
2.选中线段 和AB的度量值; 选中线段AB和 的度量值 的度量值; 选中线段
返回 主菜单
参数动态地改变颜色
A
B
AB = 2.96 厘厘
2.选中线段 和AB的度量值; 选中线段AB和 的度量值 的度量值; 选中线段
返回 主菜单
请单击
参数动态地改变颜色
A
B
AB = 2.96 厘厘
3.单击菜单“显示”---“颜色”---“参数”选项 ; 单击菜单“显示” 颜色” 参数” 单击菜单 颜色 参数
请单击
返回 主菜单
参数动态地改变颜色
单击结 构/轨迹 轨迹
A
B
AB = 2.96 厘厘
动态演 示
4.选中线段 和点 ,执行“构造 轨迹”选项 ; 选中线段AB和点 和点A,执行“构造/轨迹 轨迹”
三、深度迭代和参数颜色功能
请单击
n=1.0
E A A'
E A
单击结 构再选 添加
E A’BC Nhomakorabea先绘制正方形BCA’A和新建一个参数 和新建一个参数n 先绘制正方形 和新建一个参数 取正整数), ),再选中原像一个点或多个 (取正整数),再选中原像一个点或多个 和参数n,并按住Shift键,然后执 点B、C和参数 ,并按住 、 和参数 键 变换/深度迭代 命令, 深度迭代〉 行〈变换 深度迭代〉命令,
选取与原像 点相对应的 一组初像点
选取映象点
返回 主菜单
深度迭代功能
动态演示 1
最后按“迭代”按钮。即可得到动态迭代的像。选中参数 , 最后按“迭代”按钮。即可得到动态迭代的像。选中参数n,按 号键, 号键, “+”号键,增加迭代,按“-”号键,减少迭代。 号键 增加迭代, 号键 减少迭代。
返回 主菜单
返回 主菜单
参数动态地改变颜色
A
B
AB = 2.96 厘厘
1.画一个三角形 取内部和点 、B,连接 画一个三角形, 取内部和点A、 ,连接AB,并度量长度; 并度量长度; 画一个三角形 并度量长度
用一个甚至多个参数动态地改变颜色,使得色彩更加丰富, 用一个甚至多个参数动态地改变颜色,使得色彩更加丰富, 演示效果更加动感
返回 主菜单
万花筒
动态演 示
返回 主菜单
