2020-2021 六年级数学比例 培优题
2020-2021六年级数学培优试卷(比例和反比例).docx
2020-2021 六年级数学培优试卷 ( 比例和反比例 )一、比例和反比例1．一个会议室用边长为 4 分米的方砖铺地，需要750 块。
如果改用边长为 5 分米的方砖铺地，需要多少块? (用比例解答 )【答案】解：设需要x 块。
5× 5× x=4 × 4× 750x=480答：需要 480 块。
【解析】【分析】设出需要 5 分米的地砖 x 块，根据总面积不变列出比例关系，求出未知数，解答即可。
2．某工程队要用长8m 的新水管替换长5m 的旧水管，原来已铺的旧水管有124 根，现在有 75 根新水管，够用吗 ?（用比例知识解答）【答案】解：设新水管需要 x 根。
8x=124 ×5x=77.577.5>75答： 75 根新水管不够用。
【解析】【分析】可以设新水管需要x 根，题目中存在的等量关系是旧水管的根数×旧水管的长度 =新水管的长度×新水管的根数，即可解得新水管需要的根数，然后于75 作比较，如果比 75 大，说明不够，如果比75 小，说明够了。
3．从甲地到乙地，小华用了 5 小时，小红用了 3 小时。
小华和小红所用的时间的比是________，他们的速度比是________。
【答案】5∶ 3； 3∶5【解析】【解答】解：小华和小红所用的时间的比是5： 3，他们的速度比是3： 5。
故答案为： 5： 3；3： 5。
【分析】路程一定，速度和时间成反比。
4．圆柱的高一定，圆柱的体积和底面积成________比例；圆柱的侧面积一定，底面周长和高成 ________比例。
【答案】正；反【解析】【解答】解：圆柱的体积÷底面积=高（一定），圆柱的体积和底面积成正比例；圆柱的底面周长×高 =侧面积（一定），圆柱的底面周长和高成反比例。
故答案为：正；反。
【分析】根据圆柱的体积公式和侧面积公式分别判断圆柱的体积和底面积、圆柱的底面周长和高的商一定还是乘积一定，如果商一定就成正比例，如果乘积一定就成反比例。
2020-2021六年级数学培优试卷(比例和反比例 )
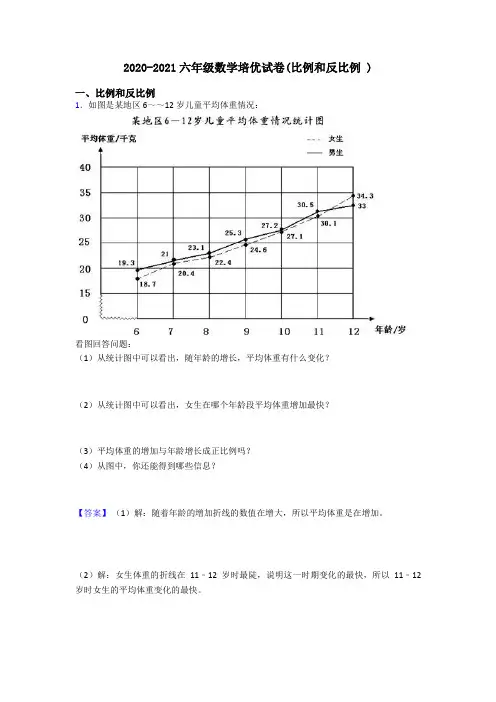
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．如图是某地区6～～12岁儿童平均体重情况：看图回答问题：（1）从统计图中可以看出，随年龄的增长，平均体重有什么变化？（2）从统计图中可以看出，女生在哪个年龄段平均体重增加最快？（3）平均体重的增加与年龄增长成正比例吗？（4）从图中，你还能得到哪些信息？【答案】（1）解：随着年龄的增加折线的数值在增大，所以平均体重是在增加。
（2）解：女生体重的折线在11﹣12岁时最陡，说明这一时期变化的最快，所以11﹣12岁时女生的平均体重变化的最快。
（3）解：男生6岁时的平均体重是19.3千克，体重与年龄的比值是：19.3：6≈3.2；当男生7岁时平均体重是21千克，体重与年龄的比值是：21：7=3；比值不相同，所以体重的增加与年龄的增长不成正比例。
（4）解：由图可知：11岁之前，男生和女生体重的增长速度相当，但11﹣﹣12岁女生体重增长的速度要快于男生【解析】【分析】（1）观察复式折线统计图可知，两条折线都是上升趋势，说明：随着年龄的增加，折线的数值在增大，所以平均体重是在增加；（2）观察女生的折线可知，女生体重的折线在11~12岁时最陡，说明这一时期变化的最快，所以11~12岁时女生的平均体重变化的最快；（3）根据题意可知，可以求出体重与年龄的比值，然后对比比值，比值不相等，则不成正比例；（4）观察统计图可知，11岁之前，男生和女生体重的增长速度相当，但11~12岁女生体重增长的速度要快于男生，据此解答.2．甲乙两地相距440千米，一辆汽车从甲地开往乙地，3时行了240千米，照这样计算，几小时可以到达乙地？（用比例解）【答案】解：设小时可以到达乙地，答：5.5小时可以到达乙地。
【解析】【分析】“照这样计算”的意思就是汽车的速度不变，路程与时间成正比例；设出未知数，根据速度不变列出比例，解比例求出到达乙地的速度即可。
3．一辆汽车在公路上行驶，行驶的时间和路程如下图。
【数学】六年级数学培优试卷(比例)
【数学】六年级数学培优试卷( 比率 )一、比率1．在下边各比中，能与∶构成比率的是()。
A. 4∶3B. 3∶4C.∶3【答案】A【分析】【解答】解：：=4：3。
故答案为： A。
【剖析】依据比率的定义，比值相等的两个比能够构成比率。
2．假如 5a=6b，那么 a： b=（）。
A. 5：6B. 6：5C. 3：2D. 2：3【答案】B【分析】【解答】解： a：b=6： 5。
故答案为： B。
【剖析】依据比率的基天性质，把 a 和 5 看作两个外项， b 和 6 看作两个内项即可。
3．比率尺是表示（）。
A. 图上距离是实质距离的B. 实质距离是图上距离是800000 倍C. 实质距离与图上距离的比是1：800000D. 实质距离是图上距离是2400000 倍【答案】 B【分析】【解答】解： 8 千米 =800000 厘米，A、图上距离是实质距离的，此选项错误；B、实质距离是图上距离的800000 倍，此选项正确；C、实质距离与图上距离的比是800000 ： 1，此选项错误；D、实质距离是图上距离的800000 倍，此选项错误。
故答案为： B。
【剖析】这是线段比率尺，表示图上 1 厘米相当于实质 8 千米，把 8 千米换算成厘米，而后依据比率尺的意义确立每个选项能否正确即可。
4．与∶能构成比率的是（）。
A. ∶B.∶C.∶【答案】C【分析】【解答】解：=1.5；A、=，不可以构成比率；B、，不可以构成比率；C、，能构成比率。
故答案为： C。
【剖析】表示两个相等的比叫做比率，由此计算出每个比的比值并选出比值相等的两个比构成比率即可。
5．在比倒尺为 1： 6000000 地图上，量得 A、 B 两地的距离为 2.5cm，一辆汽车以每小时 75km 的速度从 A 地开往 B 地， ________小时能够抵达。
【答案】2【分析】【解答】 2.5 ÷=2.5 ×6000000=15000000（ cm） =150（千米）；150 ÷ 75=2（小时）。
六年级数学比例和反比例培优题(20211109215922)
六年级数学比率和反比率培优题一、比率和反比率1．把一瓶果汁均匀分红若干杯，分的杯数和每杯的果汁量以下表。
分的杯数/杯 6 5 43每杯的果汁量/mL 100 120 （） 200（1）请把上表增补完好。
（2）分的杯数和每杯的果汁量有什么关系?为何？（3）假如把这些果汁均匀分红 10 杯，每杯的果汁量是多少毫升？【答案】（ 1） 150（2）解：成反比率，因为每杯的果汁量×分的杯数=果汁总量。
（3）解： 6×100÷10=60（毫升）答：每杯的果汁量是60 毫升。
【分析】【解答】解：（1） 100×6÷4=150（ mL）【剖析】（ 1）这瓶果汁的总量不变，用总量除以 4 即可求出每杯的容量；（2）依据正反比率关系的意义确立这两个量的关系；（3）用果汁总量除以 10 即可求出每杯果汁的容量。
2．学校买来一批课外书，准备散发到各班。
假如每班发15 本，能够发给24 个班，假如每班发 10 本，能够发给多少个班?（列比率解答）【答案】解：设能够散发给x 个班。
10x=15 × 24x=36答：能够发给36 个班。
【分析】【剖析】依据题意，这批课外书的总数不变，设假如每班发10 本，能够发给x 个班，则依据总数=每班散发数目×班数列出方程，求解方程即可。
3．妈妈有一辆自行车， A 和 B 是自行车的两个齿轮（如图），骑车时用脚驱动 A 带动 B，进而使自行车行进。
（1）这辆自行车，齿轮 A 有 50 个齿，齿轮 B 有 20 个齿。
当齿轮 A 转动 1 圈时，齿轮B转动多少圈？（2）这辆自行车的车轮直径约是 60cm，妈妈每日上班的行程大概是 3000m。
妈妈骑车上班大概要置多少圈（即齿轮 A 转动的圈数） ?（计算时π取 3，最后结果保存整数）【答案】（ 1）解： 50×1÷20=2（.5圈）答：齿轮 B 转动 2.5 圈。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．一个会议室用边长为4分米的方砖铺地，需要750块。
如果改用边长为5分米的方砖铺地，需要多少块? (用比例解答)【答案】解：设需要x块。
5×5×x=4×4×750x=480答：需要480块。
【解析】【分析】设出需要5分米的地砖x块，根据总面积不变列出比例关系，求出未知数，解答即可。
2．某工程队要用长8m的新水管替换长5m的旧水管，原来已铺的旧水管有124根，现在有75根新水管，够用吗?（用比例知识解答）【答案】解：设新水管需要x根。
8x=124×5x=77.577.5>75答：75根新水管不够用。
【解析】【分析】可以设新水管需要x根，题目中存在的等量关系是旧水管的根数×旧水管的长度=新水管的长度×新水管的根数，即可解得新水管需要的根数，然后于75作比较，如果比75大，说明不够，如果比75小，说明够了。
3．30kg花生仁能榨出花生油12kg。
照这样计算，要榨出48t花生油,需要花生仁多少吨? 【答案】解：设需要花生仁x吨，12：30=48：x12x=30×48x=1440÷12x=120答：需要花生仁120t.【解析】【分析】花生油的出油率是不变的，花生仁的质量和花生油的质量成正比例，设出未知数，根据出油率不变列出比例解答即可.4．0.3x=0.5y，那么y与x的比值是________，x与y成________比例。
【答案】；正【解析】【解答】 0.3x=0.5y，那么y与x的比值是， x与y成正比例。
故答案为：；正。
【分析】根据比例的基本性质可知，相乘的两个数同时作外项或内项，然后化简求出比值；两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系，据此解答。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．服装厂加工一批服装，计划每天加工120套，50天可以完成。
实际每天加工了150套，多少天可以加工完？（用比例解）【答案】解：设x天可以加工完。
150x=120×50x=6000÷150x=40答：40天可以加工完。
【解析】【分析】这批服装的总数不变，每天加工的套数与加工的天数成反比例，设出未知数，根据总套数不变列出比例，解比例求出实际加工的天数即可。
2．表中x和y是两个成比例的量，观察表格并填完整。
X36181210y51020X361812109y510151820空位中x和y的值。
3．一个滴水的水龙头滴水的时间和所浪费的水量如下表：滴水时间/分1020304050浪费水量/L0.61.21.82.43.0（1）在上图中描出表示滴水时间和相应浪费水量的点，然后把它们按顺序连起来。
（2）根据图象进行分析：滴水25分钟浪费的水有________L，滴水________分钟就会浪费2.7L的水。
滴水时间和浪费的水量成________比例。
（3）针对这一现象，你想说点什么呢?【答案】（1）解：（2）1.5；45；正（3）解：要珍惜水资源，注意节约用水。
（合理即可）【解析】【解答】（2）滴水25分钟浪费的水有1.5L，滴水45分钟就会浪费2.7L水；滴水时间和浪费的水量成正比例。
故答案为：（2）1.5；45；正。
【分析】（1）先描出对应的点，然后连接成一条线即可；（2）找出25分钟对应的点，然后确定浪费的水量；找出2.7L对应的点，然后确定对应的时间，根据图像可以直接判断两个量成正比例；（3）说出自己合理的观点即可。
4．补充表格。
药粉/克1246810水/克200400；2000【解析】【解答】因为200：1=200÷1=200，400：2=400÷2=200，所以水的质量：药粉的质量=200，则水的质量分别为：4×200=800（克），6×200=1200（克），8×200=1600（克），10×200=2000（克），根据计算，填空如下：【分析】根据题意可知，先求出水的质量与药粉质量的比，水的质量：药粉的质量=200，它们的比值一定，水和药粉的质量成正比例，用药粉的质量×200=水的质量，据此计算填空即可.5．a÷b=35，那么a与b成________比例关系，如果 = ，那么a与b成________比例关系．【答案】正；反【解析】【解答】解：a÷b=35，a与b的商一定，a与b成正比例关系；，则ab=35，所以a与b从反比例关系。
2020-2021六年级数学培优试卷(比例 )
2020-2021六年级数学培优试卷(比例 )一、比例1．把一个长5毫米的零件画在图纸上是1分米，这张图纸的比例尺是（）。
A. 5：1B. 200：1C. 20：1【答案】 C【解析】【解答】1分米：5毫米=100毫米：5毫米=（100÷5）：（5÷5）=20：1。
故答案为：C。
【分析】已知图上距离与实际距离，要求比例尺，用图上距离：实际距离=比例尺，据此列式解答。
2．下面能与6：组成比例的是（）A. ：6B. 3：C. 9：D. 3：【答案】 B【解析】【解答】解：6：=18；A、，不能组成比例；B、=18，能组成比例；C、，不能组成比例；D、=27，不能组成比例。
故答案为：B。
【分析】比例是表示两个比相等的式子，所以比值相等的两个比才能组成比例。
3．下面（）能和：4组成比例。
A. 5：10B.C.【答案】 C【解析】【解答】：4=÷4=；选项A，5：10=5÷10=，≠，不能组成比例；选项B，：=÷=，≠，不能组成比例；选项C，：=÷=，=，能组成比例。
故答案为：C。
【分析】表示两个比相等的式子叫比例，判断两个比是否能组成比例，用前项÷后项=比值，分别求出比值，如果比值相等，就能组成比例，否则，不能组成比例，据此解答。
4．应用比例的基本性质，下面（）组中的两个比可以组成比例。
A. 和B. 0.2：10和2：50C. 和【答案】 C【解析】【解答】解：×==×，能组成比例。
故答案为：C。
【分析】根据比列的基本性质，假设两个比可以组成比例，如果两内项之积等于两外项之积，即可组成比例。
5．下列各组中两个比能组成比例的是（）。
A. 和B. 40：10和1：4C. 1.2：0.4和：D. ：2和：5【答案】 C【解析】【解答】解：A、：2=，，不能组成比例；B、40：10=4，1：4=0.25，不能组成比例；C、1.2：0.4=3，，能组成比例；D、，，不能组成比例。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．铁路工人铺一条铁轨，计划每天铺400米，18天完成，实际每天比计划多铺50米，实际多少天完成?【答案】解：400×18÷（400+50）=16（天）答：实际16天完成。
【解析】【解答】解：设实际x天完成。
（400+50）x=400×18x=7200÷450x=16答：实际16天完成。
【分析】铁轨的总长度不变，每天铺的长度与铺的天数成反比例，设出未知数，根据铁轨的总长度不变列出比例，解比例求出未知数的值即可。
2．一列火车行驶720km需要3小时。
照这样计算，从甲地到乙地的铁路长约1200千米，这列火车需要行驶几小时? (用比例解答)【答案】解：设需要行驶x小时。
=x=5答：需要行驶5小时。
【解析】【分析】设这列火车需要行x小时，根据火车速度不变列出正比例关系，求出未知数，解答即可。
3．一个会议室用边长为4分米的方砖铺地，需要750块。
如果改用边长为5分米的方砖铺地，需要多少块? (用比例解答)【答案】解：设需要x块。
5×5×x=4×4×750x=480答：需要480块。
【解析】【分析】设出需要5分米的地砖x块，根据总面积不变列出比例关系，求出未知数，解答即可。
4．小兰看一本故事书，每天看10页，12天看完，若每天看15页，几天可以看完?【答案】解：设x天可以看完。
10×12=15x解得x=8答：8天可以看完。
【解析】【分析】已知每天看的页数×对应看完的天数=预计每天看的页数×对应预计看完的天数。
等式的性质2：等式两边同时乘（或除以）一个相同的数或式子，两边依然相等。
5．一批零件20人去做需要15天，照这样计算，如果增加5人，几天可以做完？【答案】解：20×15÷(20+5)=300÷25=12(天)答：12天可以做完.【解析】【分析】做这批零件的工作量是不变的，用20乘15求出工作量，然后除以现在的人数即可求出可以做完的天数.6．图上距离一定，实际距离和比例尺成正比例。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．铁路工人铺一条铁轨，计划每天铺400米，18天完成，实际每天比计划多铺50米，实际多少天完成?【答案】解：400×18÷（400+50）=16（天）答：实际16天完成。
【解析】【解答】解：设实际x天完成。
（400+50）x=400×18x=7200÷450x=16答：实际16天完成。
【分析】铁轨的总长度不变，每天铺的长度与铺的天数成反比例，设出未知数，根据铁轨的总长度不变列出比例，解比例求出未知数的值即可。
2．表中x和y是两个成比例的量，观察表格并填完整。
空位中x和y的值。
3．一个会议室用边长为4分米的方砖铺地，需要750块。
如果改用边长为5分米的方砖铺地，需要多少块? (用比例解答)【答案】解：设需要x块。
5×5×x=4×4×750x=480答：需要480块。
【解析】【分析】设出需要5分米的地砖x块，根据总面积不变列出比例关系，求出未知数，解答即可。
4．两个咬合在一起的齿轮，主动轮有50个齿，每分钟转100转；从动轮有20个齿，每分钟转多少转?【答案】解：设从动轮每分钟转x转，则20x=50×10020x=5000x=250答：从动轮每分钟转250转。
【解析】【分析】由于两齿轮咬合在一起，它们必须在相同时间内转过相等的齿数，设从动齿轮每分钟转x转，则有：50×100=20x，就可解答此题．5．为了保护环境，净化空气，六年级同学要去植树，原计划每小时植树40棵，3小时植完。
实际每小时比原计划多植树20棵，实际提前几小时完成任务?【答案】1小时【解析】【解答】解：设实际提前x小时完成任务40：（40+20）=（3-x）：360×(3-x)=1203-x=2x=1答：实际提前1小时完成任务【分析】同学要植树的总棵数是一定的，每小时植树棵数与时间成反比。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．工人铺一条路，用边长4分米的方砖铺需要500块，如果改用边长5分米的方砖铺，需要多少块？【答案】解：设需要x块，4×4×500＝5×5×x25x＝8000x＝320答：如果改用边长5分米的方砖铺地，需要320块。
【解析】【分析】此题主要考查了反比例应用题，这条路的总面积是一定的，每块砖的面积与铺的块数成反比例，据此列比例解答.2．“浪漫一身”服装厂制作一批新款女式短裙，每条用布料1.2米，制作100条、200条、300条这样的短裙各需用布料多少米？将相应的米数填在表中。
（1）（3）用660米布料可以制作多少条这种短裙？【答案】（1）120；240；360；480；600（2）解：1.2×450=540（米）答：一共需要布料540米。
（3）解：660÷1.2=550（条）答：可以制作550条这种短裙。
【解析】【分析】（1）根据题意，用每条短裙用布的米数×短裙数量=一共需要用布的总米数，据此列式计算，然后填表即可；（2）要求制作450条这种短裙，一共需要布料多少米，用每条短裙用布的米数×短裙数量450=一共需要用布的总米数，据此列式解答；（3）要求660米布料可以制作多少条这种短裙，用布料的总米数÷每条短裙用布的米数=制作的短裙数量，据此列式解答.3．给一间房子铺地，如果用边长6分米的方砖，需要80块。
如果改用边长8分米的方砖，需要多少块？【答案】解：设需要x块。
（8×8）x=6×6×8064x=2880x=2880÷64x=45答：需要45块。
【解析】【分析】每块方砖的面积×方砖的块数=房间的面积，每块方砖的面积与方砖的块数成反比例；设出未知数，根据总面积不变列出比例，解比例求出需要方砖的块数即可。
2020-2021北师大六年级下《比例 》培优训练
2020-2021北师大六年级下《比例》培优训练一、比例1．把一个长8m，宽6m的长方形画在作业本上，选择比例尺比较合适的是（）。
A. 1：10B. 1：100C. 1：10000【答案】 B【解析】【解答】解：8m=800cm，A、800×=80（cm），不合适；B、800×=8（cm），合适；C、800×=0.08（cm），不合适。
故答案为：B。
【分析】把实际的长度换算成厘米，然后用实际长度乘比例尺，求出图上长度，根据实际情况选择合适的比例尺即可。
2．下面不能组成比例的是( )。
A. 10∶12=35∶42B. 4∶3=60∶45C. 20∶10=60∶20【答案】 C【解析】【解答】解：因为12×35=420，10×42=420，所以10：12和35：42能组成比例；因为3×60=180，4×45=180，所以4：3和60：45能组成比例；因为10×60=600，20×20=400，所以20、10、60、20不能组成比例。
故答案为：C。
【分析】比例的基本性质：比例的内项之积等于比例的外项之积。
3．人的体重和身高( )。
A. 不成比例B. 成正比例C. 成反比例【答案】 A【解析】【解答】解：人的体重和身高虽是两种相关联的量，但是它们的乘积或比值都不一定，所以不成比例。
故答案为：A。
【分析】判断两种量成正比例还是反比例的办法：当这两种相关联的量中相对应的两个数的商一定时，这两个数就成正比例关系；反之，当这两个数的积一定时，这两个数就成反比例关系。
4．如果5a=6b，那么a：b=（）。
A. 5：6B. 6：5C. 3：2D. 2：3【答案】 B【解析】【解答】解：a：b=6：5。
故答案为：B。
【分析】根据比例的基本性质，把a和5看作两个外项，b和6看作两个内项即可。
5．一个长方形按4∶1的比放大后，得到的图形与原图形比较，下列说法中正确的是（）。
2020-2021 六年级下册数学培优-第一讲-比例
2020-2021 六年级下册数学培优-第一讲-比例一、比例1．下面（）能和：4组成比例。
A. 5：10B.C.【答案】 C【解析】【解答】：4=÷4=；选项A，5：10=5÷10=，≠，不能组成比例；选项B，：=÷=，≠，不能组成比例；选项C，：=÷=，=，能组成比例。
故答案为：C。
【分析】表示两个比相等的式子叫比例，判断两个比是否能组成比例，用前项÷后项=比值，分别求出比值，如果比值相等，就能组成比例，否则，不能组成比例，据此解答。
2．在下面各比中，能与组成比例的是（）。
A. 4：3B. 3：4C.D. 8：6【答案】 B【解析】【解答】：=÷=；选项A，4：3=4÷3=；选项B，3：4=3÷4=；选项C，：=÷=；选项D，8：6=8÷6=；：=3：4.故答案为：B.【分析】根据比例的意义：表示两个比相等的式子叫比例，据此先求出原题中比的比值，用前项÷后项=比值，然后求出各选项的比值，并进行对比，比值相等就能组成比例，据此解答.3．下面各组的两个比，可以组成比例的是（）A. ：和：B. 12：9和9：6C. 8.4：2.1和1.2：8.4【答案】 A【解析】【解答】解：A、，=2，能组成比例；B、12：9=， 9：6=，不能组成比例；C、8.4：2.1=4，1.2：8.4=0.25，不能组成比例。
故答案为：A。
【分析】比值相等的两个比能组成比例，计算出每个选项中两个比的比值即可作出选择。
4．比例尺一定，实际距离扩大到原来的5倍，则图上距离( )。
A. 缩小到原来的B. 扩大到原来的5倍C. 不变【答案】 B【解析】【解答】解：因为图上距离=实际距离×比例尺，所以当比例尺一定时，实际距离扩大到原来的5倍，则图上距离也将扩大到原来的5倍。
故答案为：B。
【分析】图上距离=实际距离×比例尺。
2020-2021 六年级数学比例和反比例 培优题
2020-2021 六年级数学比例和反比例培优题一、比例和反比例1．京沪高铁的火车行驶路程与时间如下表：路程/千米80160240480……时间/时1236……（1）在上图中描出表示路程与时间相对应的点，然后把它们按顺序连起来。
（2）利用画出的图像估计一下，时间3.5小时的路程是________千米。
【答案】（1）根据分析，作图如下：（2）280【解析】【解答】（2）利用画出的图像估计一下，时间 3.5小时的路程是：3.5×80=280（千米）.故答案为：280。
【分析】（1）观察统计图可知，纵轴表示路程，横轴表示时间，根据表中数据先描点，再连线，据此作图；（2）根据题意，用时间×速度=路程，据此列式解答.2．表中x和y是两个成比例的量，观察表格并填完整。
X36181210y51020X361812109y510151820空位中x和y的值。
3．小兰看一本故事书，每天看10页，12天看完，若每天看15页，几天可以看完?【答案】解：设x天可以看完。
10×12=15x解得x=8答：8天可以看完。
【解析】【分析】已知每天看的页数×对应看完的天数=预计每天看的页数×对应预计看完的天数。
等式的性质2：等式两边同时乘（或除以）一个相同的数或式子，两边依然相等。
4．补充表格。
药粉/克1246810水/克200400；2000【解析】【解答】因为200：1=200÷1=200，400：2=400÷2=200，所以水的质量：药粉的质量=200，则水的质量分别为：4×200=800（克），6×200=1200（克），8×200=1600（克），10×200=2000（克），根据计算，填空如下：【分析】根据题意可知，先求出水的质量与药粉质量的比，水的质量：药粉的质量=200，它们的比值一定，水和药粉的质量成正比例，用药粉的质量×200=水的质量，据此计算填空即可.5．圆柱的高一定，圆柱的体积和底面积成________比例；圆柱的侧面积一定，底面周长和高成________比例。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．某工程队要铺设一条公路，前20天已铺设了2.8千米，照这样计算，剩下的4.2千米，还要多少天才能铺完?(用比例解)【答案】解：设还要x天才能铺完。
2.8∶20=4.2∶xx=30答：还要30天才能铺完。
【解析】【分析】照这样计算的意思就是每天铺的长度不变，铺的长度与天数成正比例，先设出未知数，根据每天铺的长度不变列出比例解答即可。
2．学校买来一批课外书，准备分发到各班。
如果每班发15本，可以发给24个班，如果每班发10本，可以发给多少个班?（列比例解答）【答案】解：设可以分发给x个班。
10x=15×24x=36答：可以发给36个班。
【解析】【分析】根据题意，这批课外书的总数不变，设如果每班发10本，可以发给x个班，则根据总数=每班分发数量×班数列出方程，求解方程即可。
3．妈妈有一辆自行车，A和B是自行车的两个齿轮（如图），骑车时用脚驱动A带动B，从而使自行车前进。
（1）这辆自行车，齿轮A有50个齿，齿轮B有20个齿。
当齿轮A转动1圈时，齿轮B 转动多少圈？（2）这辆自行车的车轮直径约是60cm，妈妈每天上班的路程大约是3000m。
妈妈骑车上班大约要置多少圈（即齿轮A转动的圈数）?（计算时π取3，最后结果保留整数）【答案】（1）解：50×1÷20=2.5（圈）答：齿轮B转动2.5圈。
（2）解：60cm=0.6m3000÷（0.6×3×2.5）≈667（圈）答：妈妈骑车上班大约要置667圈。
【解析】【分析】（1）根据题意可知，用齿轮A的齿数×转动的圈数÷齿轮B的齿数=齿轮B转动的圈数，据此列式解答；（2）根据题意可知，先求出自行车齿轮B每圈走过的路程，用周长公式：C=πd，然后根据齿轮A转1圈，齿轮B转2.5圈，可以求出齿轮A每圈走过的路程，用齿轮B每圈走过的路程×齿轮B转动的圈数=齿轮A每圈走过的路程，最后用上班的总路程÷齿轮A每圈走过的路程=齿轮A转动的圈数，据此列式解答，结果保留整数.4．乐乐买了一个军舰模型，包装盒上写着“按1：400制作”，他量了一下，模型长45cm。
2020-2021六年级数学培优试卷(比例和反比例 )
2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1．同一时间、同一地点测得的树高和它的影长如下表：树高/米2346…影长/米1.62.43.24.8…（2）树高和影长成什么比例?为什么？（3）量得一颗大树的影长是10.4米，这棵大树有多高？【答案】（1）（2）解：成正比例。
因为 =1.25， =1.25， =1.25， =0.8（一定），所以，树高和影长成正比例。
（3）解：设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答：这棵大树的高度是13米。
【解析】【分析】（1）观察统计图可知，横轴表示树高，竖轴表示影长，据此先描点，再连线，据此作图；（2）分别用树高：影长，求出比值，当比值一定时，成正比例，据此判断；（3）根据题意可知，设这棵大树的高度是x米，用树高：影长=树高：影长，据此列正比例解答.2．一列火车行驶720km需要3小时。
照这样计算，从甲地到乙地的铁路长约1200千米，这列火车需要行驶几小时? (用比例解答)【答案】解：设需要行驶x小时。
=x=5答：需要行驶5小时。
【解析】【分析】设这列火车需要行x小时，根据火车速度不变列出正比例关系，求出未知数，解答即可。
3．两个咬合在一起的齿轮，主动轮有50个齿，每分钟转100转；从动轮有20个齿，每分钟转多少转?【答案】解：设从动轮每分钟转x转，则20x=50×10020x=5000x=250答：从动轮每分钟转250转。
【解析】【分析】由于两齿轮咬合在一起，它们必须在相同时间内转过相等的齿数，设从动齿轮每分钟转x转，则有：50×100=20x，就可解答此题．4．化肥厂生产一批化肥，每天生产35吨，40天完成任务。
如果要28天完成任务，那么每天应生产多少吨?(用比例知识解答)【答案】解：设每天应生产x吨.28x=35×40x=1400÷28x=50答：每天应生产50吨.【解析】【分析】这批化肥的总质量不变，每天生产的质量和天数成反比例，设出未知数，根据总质量不变列出比例解答即可.5．用边长15厘米的方砖给房间铺地需要2000块，如果改用边长为25厘米的方砖铺地，需要多少块?【答案】解：设需要x块。
2021小学六年级教学数学培优习题比例以及反比例
2020-2021 六年级数学培优试卷 ( 比率和反比率 )一、比率和反比率1．一个会议室用边长为 4 分米的方砖铺地，需要750 块。
假如改用边长为 5 分米的方砖铺地，需要多少块? (用比率解答 )【答案】解：设需要x 块。
5× 5× x=4 × 4× 750x=480答：需要 480 块。
【分析】【剖析】设出需要 5 分米的地砖 x 块，依据总面积不变列出比率关系，求出未知数，解答即可。
2．某工程队要用长8m 的新水管替代长5m 的旧水管，本来已铺的旧水管有124 根，此刻有 75 根新水管，够用吗 ?（用比率知识解答）【答案】解：设新水管需要 x 根。
8x=124 ×577.5>75答： 75 根新水管不够用。
【分析】【剖析】能够设新水管需要x 根，题目中存在的等量关系是旧水管的根数×旧水管的长度 =新水管的长度×新水管的根数，即可解得新水管需要的根数，而后于75 作比较，如果比 75 大，说明不够，假如比75 小，说明够了。
3．从甲地到乙地，小华用了 5 小时，小红用了 3 小时。
小华和小红所用的时间的比是________，他们的速度比是________。
【答案】5∶ 3； 3∶5【分析】【解答】解：小华和小红所用的时间的比是5： 3，他们的速度比是3： 5。
故答案为： 5： 3；3： 5。
【剖析】行程必定，速度和时间成反比。
4．圆柱的高必定，圆柱的体积和底面积成________比率；圆柱的侧面积必定，底面周长和高成 ________比率。
【答案】正；反【分析】【解答】解：圆柱的体积÷底面积=高（必定），圆柱的体积和底面积成正比率；圆柱的底面周长×高 =侧面积（必定），圆柱的底面周长和高成反比率。
故答案为：正；反。
【剖析】依据圆柱的体积公式和侧面积公式分别判断圆柱的体积和底面积、圆柱的底面周长和高的商必定仍是乘积必定，假如商必定就成正比率，假如乘积必定就成反比率。
2020-2021人教版六年级数学比例 测试卷附答案
2020-2021人教版六年级数学比例测试卷附答案一、比例1．已知AB=K， =D，（ABCD都是大于0的自然数），那么下列比例中正确的是（）A. B. C. D.【答案】 D【解析】【解答】解：是正确的。
故答案为：D。
【分析】AB=K，=D，那么=D，所以AB=CD，据此作答即可。
2．应用比例的基本性质，下面（）组中的两个比可以组成比例。
A. 和B. 0.2：10和2：50C. 和【答案】 C【解析】【解答】解：×==×，能组成比例。
故答案为：C。
【分析】根据比列的基本性质，假设两个比可以组成比例，如果两内项之积等于两外项之积，即可组成比例。
3．已知a：b=c：d，若将b乘5，使比例不成立的条件是( )。
A. a乘5B. c除以5C. d除以5【答案】 C【解析】【解答】因为 a：b=c：d ；所以bc=ad；bx5xc=ax5xd；bx5xc÷5=bc=ad故答案为：C【分析】由比例的基本性质可知，bc=ad，若将b乘5，等式左边扩大到原来的5倍，若d 除以5，等式的右边缩小到原来的.因此，等式不成立，即比例也不成立。
4．实验小学新建一个长方形游泳池，长50米，宽30米。
选用比例尺（）画出的平面图最大。
A. 1∶1000B. 1∶1500C. 1∶500【答案】 C【解析】【解答】解：50米=5000厘米，30米=3000厘米，选用1：1000比例尺，在平面图中画出的长是5000÷1000=5厘米，宽是3000÷1000=3厘米，面积是5×3=15平方厘米；选用1：1500比例尺，在平面图中画出的长是5000÷1500≈3.3厘米，宽是3000÷1500=2厘米，面积是 3.3×2=6.6平方厘米；选用1：500比例尺，在平面图中画出的长是5000÷500=10厘米，宽是3000÷500=6厘米，面积是10×6=60平方厘米。
2020-2021学年北师大版数学六年级下册第二单元《比例》培优检测卷
2020-2021学年北师大版数学六年级下册第二单元《比例》培优检测卷学校:___________姓名：___________班级：___________考号：___________一、填空题1．一幅地图上，图上2厘米表示实际距离80千米，这幅地图的比例尺是______．2．一个三角形，三个内角的度数比是1：2：3，这是一个什么三角形？3．甲、乙两数的比是2：5，甲数是40，乙数是．4．一幅图的比例尺是。
A，B两地相距140 km，画在这幅图上应是（____）cm。
5．如果5x＝8y（x、y≠0），那么________∶________＝5∶8。
6．被减数是160，减数与差的比是5:3，减数是（______）。
7．甲数比乙数多30%甲数和乙数的比是（__________）．8．把改写成数值比例尺是（______）。
9．一幅图的比例尺为1：6000000，量得甲地到乙到地的距离为15厘米，这两地的实际距离是千米．10．A，B两地的实际距离是120km，在一幅地图上，量得两地相距3cm这幅地图的比例尺是．二、选择题11．甲数的与乙数的相等，那么甲数与乙数的比是（）A．8：9 B．9：8 C．1：412．打一份稿件，甲用6分钟，乙用8分钟，甲乙两人工作效率的最简比（）A．6:8 B．8:6C．3:4 D．4:313．将线段比例尺改写成数值比例尺是（）。
A．1∶40 B．1∶400000 C．1∶4000000 D．1∶4000 14．一个机器零件的长度是8毫米，画在比例尺是10：1的图纸上的长度是（）A．8分米B．8毫米C．8厘米15．如果图上距离3厘米表示实际距离1.5毫米，那么这幅图的比例尺是（）A．1：20 B．1：2 C．20：116．根据3a=5b可以写成（）A．3：a=5：b B．a：b=5：3 C．a：b=3：5 D．a：5=3：b17．在比例尺是1：100000的平面图上，实际距离是1000m，在图上是（）。
2020-2021北师大六年级下《比例 》培优训练
2020-2021北师大六年级下《比例》培优训练一、比例1．一个零件的高是4mm，在图纸上的高是2cm．这幅图纸的比例尺是（）A. 1：5B. 5：1C. 1：2D. 2：1【答案】 B【解析】【解答】解：2cm=20mm，比例尺：20：4=5：1。
故答案为：B。
【分析】把2cm换算成mm，然后写出图上距离与实际距离的比并化成后项是1的比就是这幅图的比例尺。
2．在一幅比例尺是1:5000000的地图上，量得甲、乙两地的距离是5cm，那么甲、乙两地的实际距离是（）km。
A. 2500B. 250C. 9【答案】 B【解析】【解答】5÷=25000000（厘米）；25000000厘米=250千米故答案为：B【分析】应用比例尺=图上距离：实际距离，得出图上距离÷比例尺=实际距离。
比例尺是以厘米为单位，然后把得数转化成以千米为单位的数即可。
3．把一个直径4毫米的手表零件，画在图纸上的直径是8厘米，这幅图纸的比例尺是( )。
A. 1：2B. 2：1C. 1：20D. 20 2 1【答案】 D【解析】【解答】解：8厘米=80毫米，比例尺是80：4=20：1。
故答案为：D。
【分析】把图上距离换算成毫米，然后写出图上距离与实际距离的比并把比化成后项是1的比就是这幅图的比例尺。
4．下列各组中的四个数能组成比例的是（）。
A. 2、8、9和14B. 、、和C. 0.6、1.8、和2D. 、、6和5【答案】 B【解析】【解答】解：A、C、D三组数字中任意两个数字组成的比的比值都不相等，不能组成比例；B、，，能组成比例。
故答案为：B。
【分析】表示两个比相等的式子叫做比例，如果一个选项中的4个数字能够找出比值相等的两个比就能组成比例。
5．如果3a=5b（a、b≠0 ），那么a：b =________【答案】 5∶3【解析】【解答】解：如果3a=5b（a、b≠0 ），那么a：b =5∶3。
故答案为：5∶3。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020-2021 六年级数学比例培优题
一、比例
1．一个长方形游泳池长50米，宽30米，
（1）选用比例尺( )画出的平面图最大。
A. 1∶1000
B. 1∶1500
C. 1∶500
（2）选用比例尺( )画出的平面图最小。
A. 1∶1000
B. 1∶1500
C. 1∶500
【答案】（1）C
（2）B
【解析】【解答】解：图上距离=实际距离×比例尺，要选平面图最大，即要比例尺最大，所以选用比例尺1：500画出的平面图最大；同样，要选平面图最小，即要比例尺最小，所以选用比例尺1：1500画出的平面图最小。
故答案为：C；B。
【分析】图上距离=实际距离×比例尺。
2．与18：15能组成比例的一个比是（）
A. 6：30
B. ：
C. 0.25 ：
D. 5：6【答案】 A
【解析】【解答】解：18：15=1.2，
A、6：30=0.2，不能组成比例；
B、=1.2，能组成比例；
C、0.25：=0.75，不能组成比例；
D、5：6=，不能组成比例。
故答案为：B。
【分析】计算出每个比的比值，与18：15的比值相等的比才能组成一个比例。
3．如图，三角形中a边上的高为b，c边上的高为d。
根据这些信息，下列式子中，（）不成立。
A. a：c=d：b
B. a：c=b：d
C.
D.
【答案】 B
【解析】【解答】解：根据三角形面积公式可知：ab=cd，所以ab=cd，所以a：c=b：d 是不成立的。
故答案为：B。
【分析】c和d是对应的底和高，a和b是对应的底和高，根据三角形面积公式可以得到ab=cd，这样根据比例的基本性质选择不成立的比例即可。
4．一个长方形按4∶1的比放大后，得到的图形与原图形比较，下列说法中正确的是（）。
A. 面积扩大到16倍
B. 周长扩大到16倍
C. 周长缩小到
【答案】 A
【解析】【解答】解：一个长方形按4∶1的比放大后，得到的图形与原图形比较，面积扩大到原来的4×4=16倍，周长扩大到原来的4倍。
故答案为：A。
【分析】长方形的面积=长×宽，长方形的周长=2×（长+宽），一个长方形按4∶1的比放大后，此时长方形的面积=长×4×宽×4=长×宽×16=原来长方形的面积×16，此时长方形的周长=2×（长×4+宽×4）=2×（长+宽）×4=原来长方形的周长×4。
5．两个城市之间的直线距离是450千米，在一幅比例尺是1：4000000的地图上，这两个城市的图上距离是（）。
A.0.1125厘米
B.1.125厘米
C.11.25厘米
D.1125厘米.
【答案】 C
【解析】【解答】解：450千米=45000000厘米，45000000×=11.25（厘米）。
故答案为：C。
【分析】把450千米换算成厘米，然后用实际距离乘比例尺求出图上距离即可。
6．在比例尺是1：50000的图纸上，量及两点之间的距离是18厘米，这两点的实际距离是________千米．
【答案】 9
【解析】【解答】解：18÷=900000厘米=9千米，所以这两点的实际距离是9千米。
故答案为：9。
【分析】实际距离=图上距离÷比例尺，然后进行单位换算即可，即1千米=100000厘米。
7．一幅画的比例尺是，A、B两地相距140km，画在这幅图上的是________cm。
【答案】3.5
【解析】【解答】1cm：40km=1cm：4000000cm=1：4000000，
140km=14000000cm，
14000000×=3.5（cm）。
故答案为：3.5 。
【分析】根据题意可知，先把线段比例尺转化成数值比例尺，然后用实际距离×比例尺=图上距离，据此列式解答。
8．一个长方形的图纸按3：1放大后的面积是原来面积的________倍．
【答案】 9
【解析】【解答】解：3×3=9，放大后的面积是原来面积的9倍。
故答案为：9。
【分析】按3：1放大，是放大图形的长和宽，也就是长和宽分别是原来长和宽的3倍，根据长方形面积公式可知，面积扩大的倍数是长和宽扩大的倍数的乘积。
9．在一个比例中，两个外项互为倒数，其中一个内项是20，另一个内项是________。
【答案】
【解析】【解答】1÷20=。
故答案为：。
【分析】比例的基本性质：比例的内项之积等于比例的外项之积；外项之积是1，1÷其中一个内项=另一个内项。
10．如果 m= n(m、n都不为0)，那么m：n=________：________。
=
________。
【答案】 20；9；
【解析】【解答】如果m=n，那么m：n=：=20：9；
=.
故答案为：20；9；.
【分析】根据比例的基本性质：在比例里，两外项之积等于两内项之积，据此将相乘的两个数同时作外项或内项，然后化简比即可；
要求n：m，依据比例的基本性质，把与n相乘的数作外项，与m相乘的数作内项，据此解答.
11．红领巾是少先队员的标志．小号红领巾是底边和腰长分别为1m和0.6m的等腰三角形，大号红领巾是小号红领巾按一定的比例放大，已知大号红领巾底边长1.2m，求腰长？（用比例解）
【答案】解：设放大后的腰长是x米，则：
1.2：1＝x：0.6
x＝1.2×0.6
x＝0.72
答：放大后的腰长是0.72米。
【解析】【分析】此题主要考查了用比例解答应用题，设放大后的腰长是x米，用放大后的底：原来的底=放大后的腰长：原来的腰长，据此列正比例解答。
12．15辆货车运一批货物，4天运了36吨。
照这样的效率，再运3天就能运完。
这批货物共有多少吨？（用比例解）
【答案】解：设这批货物共有X吨
36:4=X:（3+4） X=63
答：这批货物共有63吨.
【解析】【分析】题意可知，应用正比例关系式：（一定）解决问题需要找到两组对应数，“照这样的效率”说明货车运送货物的效率不变，因此，36吨和4天是一组对应数，货物总吨数和运货总时间（7天）是一组对应数，两组对应数的比值相等列出比例式即可解答。
13．大雁塔高约64.5米，一个大雁塔的模型与大雁塔高度的比是1：10。
这个模型高多少米？（列比例解）
【答案】解：设这个模型高x米。
x：64.5=1：10
10x=64.5×1
x=64.5÷10
x=6.45
答：这个模型高6.45米。
【解析】【分析】先设出未知数，然后根据模型与实际高度的比是1：10列出比例，解比例求出模型的高度即可。
14．列综合算式或方程解下列各题。
（1）一个数的比它的少3.6。
这个数是多少?
（2）比例的两个外项分别是5和13，一个内项是26，另一个内项是多少？
【答案】（1）3.6÷（）
=3.6÷
=8
（2）设另一个内项是x。
26x=5×13
x=65÷26
x=2.5
【解析】【分析】（1）根据分数除法的意义，用少的数除以少的占这个数的分率即可求出这个数；
（2）设另一个内项是x，根据两个内项积等于两个外项的积列出方程，解方程求出另一个内项。
15．在比例尺是的地图上，量得两地之间的距离是8厘米，如果在比例尺是1：8000000的地图上，两地之间的距离是多少？
【答案】解：8÷ ×
＝20000000×
＝2.5（厘米）
答：如果在比例尺是1：8000000的地图上，这两地之间的距离是2.5厘米。
【解析】【分析】用图上距离除以第一幅图的比例尺求出实际距离，用实际距离乘第二幅图的比例尺即可求出在第二幅地图上两地间的距离。