同位角内错角同旁内角1
1.1同位角内错角同旁内角

1 b 4 6 2 3 4 6 索交流 变式图形:图中的∠1与∠2都是内错角
图形特征:在形如“Z”的图形中有内错角。
1
类比交流 从直线 l 来看,∠4与∠5处于哪个位置?
∠4与∠5处于直线 l 的同旁
从直线a、b来看,∠4与∠5又处于哪个位置? ∠4与∠5都处于直线a、b的之间
D
4
B
F
C
(2)若ED,BC被AF所截, ∠4 是内错角。 则∠3与_____
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(3)∠1与∠3是AB和AF被 DE 所截构成的_______ 内错 角。 _____
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
AB 和_____ AF 被 (4)∠2与∠4是_____ 同位 角。 BC所截构成的______
∠4与∠5是一对内错角.
直线AB,CD被直线EF所截
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
F Z U或 n
l2
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB所截, ∠2 是同位角。 则∠1与_____
能力挑战: 看图填空
A E
2 1 3
课内练习
1.(1)如果把图看成是直线AB,EF被 直线CD所截,那么∠1与∠2是一对什 么角?∠3与∠4呢?∠2与∠4呢?
A 1 4 E 5 2 3 F
∠1与∠2是一对同位角,
∠3与∠4是一对内错角, ∠2与∠4是一对同旁内角.
同位角、内错角、同旁外角、垂线
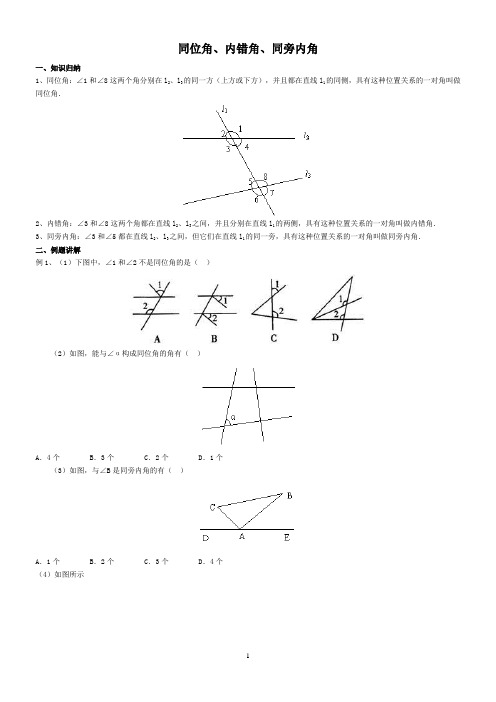
同位角、内错角、同旁内角一、知识归纳1、同位角:∠1和∠8这两个角分别在l2、l3的同一方(上方或下方),并且都在直线l1的同侧,具有这种位置关系的一对角叫做同位角.2、内错角:∠3和∠8这两个角都在直线l2、l3之间,并且分别在直线l1的两侧,具有这种位置关系的一对角叫做内错角.3、同旁内角:∠3和∠5都在直线l2、l3之间,但它们在直线l1的同一旁,具有这种位置关系的一对角叫做同旁内角.二、例题讲解例1、(1)下图中,∠1和∠2不是同位角的是()(2)如图,能与∠α构成同位角的角有()A.4个B.3个C.2个D.1个(3)如图,与∠B是同旁内角的有()A.1个B.2个C.3个D.4个(4)如图所示①AB与BC被AD所截得的内错角有_____________;②DE与AC被AD所截得的内错角有_____________;③DE与AC被BC所截得的同位角有_____________;④∠5、∠7是_____________被_____________直线所截得的_____________角;⑤∠1、∠4是_____________被_____________所截得的_____________角;⑥∠B、∠7是_____________被_____________所截得的_____________角.(5)如图,直线AB、CD、EF两两相交,请指出∠1与其它有标号的角是什么角?例2、(1)如图,下列判断错误的是()A.∠1和∠2是同旁内角B.∠3和∠4是内错角C.∠5和∠6是同旁内角D.∠5和∠8是同位角(2)如图,指出∠1、∠2、∠3、∠4、∠5中是同位角的有__________对,是内错角的有__________对,是同旁内角的有__________对.一、选择题1、如图所示,∠1和∠2是同位角的是()A.②③B.①②③C.④D.①④2、∠1与∠2不是内错角的是()3、如图所示,直线AB,CD,EF两两相交,图中共有同旁内角()A.1对B.3对C.6对D.12对4、如图所示,有以下四种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠2和∠5是同位角,其中正确的说法有()A.1个B.2个C.3个D.4个5、如图所示,AB,BE被AC所截,下列说法不正确的是()A.∠1与∠2是同旁内角B.∠1与∠ACE是内错角C.∠B与∠4是同位角D.不能得到内错角∠1与∠3二、填空题6、如图所示,∠1和∠2是两条直线____________与____________被第三条直线____________所截的____________角;∠5和∠6是两条直线____________与____________被第三条直线____________所截的____________角;∠2和∠6是两条直线____________与____________被第三条直线____________所截的____________角.7、如图所示,∠ABD的同位角有____________,内错角有____________,同旁内角有____________;∠BGH的同位角有____________,内错角有____________,同旁内角有____________.8、如图所示,直线AB,CD被BD所截构成∠3和__________是内错角,AD,BC被BD所截构成的∠1和∠2是___________角,AD,BC被AB所截构成的∠5和∠ABC是___________角,∠6和∠ABC是____________角.三、综合题9、如图所示,∠1和∠E,∠2和∠3,∠3和∠E都是什么角,它们分别是哪两条直线被哪一条直线所截得的?10、如图所示,平行直线EF,MN被相交直线AB,CD所截,请问图中有多少对同旁内角?垂线一、知识归纳1、垂直:当两条直线所有的角为90°时,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.如图,AB与CD相交于O,当交角90°时,称AB与CD垂直,记作AB⊥CD于O. 其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.两直线垂直的位置关系是用角来刻画的.2、在同一平面内,过一点有且只有一条直线与已知直线垂直.3、垂线段最短.4、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.注意:垂线段:是一个几何图形;距离:是一个数量,这个数量是垂线段的长度.5、正确理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念.如上图(1)AB与CD相交,当交角90°时,称AB与CD垂直,其中的一条直线叫做另一条直线的垂线;如图(2)过P到这条直线所引的直线中,点P与垂足E之间的线段PE叫做垂线段;P到垂足E之间的距离叫点到直线的距离;如图3,点M和点N之间的线段的长度叫两点间距离.二、例题讲解例1、(1)下列条件中,位置关系互相垂直的是()A.相邻两角的角平分线B.互为对顶角的两角的角平分线C.互为邻补角的两角的角平分线D.互为补角的两角的平分线(2)甲、乙、丙、丁四个同学在判断时针与分针在某一时刻是否互相垂直时,有下列几种说法,其中完全正确的是()A.甲说3点和3点半B.乙说6点一刻和6点3刻C.丙说9点和12点3刻D.丁说3点和9点例2、如图,根据下列语句画图:(1)过点P画射线AM的垂线,Q为垂足;(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;(3)过点P画线段AB的垂线,交线段AB延长线于Q点.例3、如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的是个数是()①点B到AC的垂线段是线段AB②线段AC是点C到AB的垂线段③线段AD是点D到BC的垂线段④线段BD是点B到AD的垂线段A.1 B.2 C.3 D.4例4、(1)如图,直线AB⊥CD于点O,点M是OC上的一个定点,点P是直线AB上的一个动点,则()A.PM>OM B.PM<OMC.PM≥OM D.PM≤OM(2)到直线l的距离等于2cm的点有()A.0个B.1个C.2个D.无数个(3)直线l上有A、B、C三点,直线l外有一点P,若PA=4cm,PB=3cm,PC=2cm,那么P点到直线l的距离()A.等于2cm B.小于2cmC.不大于2cm D.大于2cm而小于3cm(4)如图,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的取值范围是()A.小于bcmB.大于acmC.大于acm或小于bcmD.大于bcm且小于acm例5、(1)如图,直线AB与CD相交于点O,EO⊥AB于O,则图中∠1与∠2的关系是___________.(2)如图,将一张长方形的白纸折叠,使BD折到BD′处,BE折到BE′处,并且BD′与BE′在同一直线上,那么AB与BC 的位置关系是__________.(3)过一个钝角的顶点分别作这个角两边的垂线,若这两条垂线的夹角为40°,则此钝角为()A.140°B.160°C.120°D.110°例6、(1)如图,点O为直线AB上一点,ON平分∠BOC,OM⊥ON,试说明OM平分∠AOC的理由.(2)如图,AB⊥BC于B,AB=4,BC=3,AC=5,求B到AC的距离.一、选择题1、P为直线l上一点,Q为l外一点,下面画图一定可能的是()A.由P画l的垂线过Q点B.由Q画l的垂线过P点C.连接PQ使PQ⊥l D.过P或Q作l的垂线2、已知直线l外一点P,则点P到直线l的距离是指()A.点P到直线l的垂线的长度 B.点P到l的垂线C.点P到直线l的垂线段的长度 D.点P到l的垂线段3、已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数是()A.30°B.150°C.30°或150° D.以上都不对4、点P为直线l外一点,点A,B,C在直线l上,若PA=4cm,PB=5cm,PC=6cm,则点P到直线l的距离是()A.4cm B.小于4cmC.不大于4cm D.5cm5、如图所示,OA⊥BC,OM⊥ON,则图中互余的角有()A.1对B.2对C.3对D.4对6、如图所示,∠PQR=138°,SQ⊥QR,QT⊥PQ,则∠SQT等于()A.42°B.64°C.48°D.24°二、填空题7、如图所示,计划把池中的水引到C处,可过C点引CD⊥AB于D,然后沿CD开渠,可使所在的渠道最短,说明这种设计的依据是__________________.8、画图并回答:如图所示,已知点P在∠AOC的边OA上.(1)过点P画OA的垂线交OC于点B;(2)画点P到OB的垂线段PM;(3)指出上述所作的图中,线段___________的长表示P点到OB边的距离;(4)比较PM与OP的大小,并说明理由.三、综合题9、如图所示,O是直线AB上一点,OF,OC,OE是射线,OE⊥OF,若∠BOC=2∠COE,∠AOF比∠COE的4倍小8°,求∠EOC的度数.10、如图所示,∠1和∠2有公共顶点,且∠1的两边与∠2的两边分别垂直,又∠1∶∠2=5∶13,求∠1,∠2的度数.11、如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N是分别位于AB两侧的村庄.(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近;行驶到点Q的位置时,距离村庄N最近,请在图中的公路上分别画出P,Q的位置(保留画图痕迹);(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村越来越近?在哪一段路上离N村越来越近,而离村庄M却越来越远?(分别用文字表达你的结论,不必证明)。
同位角内错角同旁内角教学设计

同位角、内错角、同旁内角数学132董茜(一)教学U标:1、了解同位角、内错角、同旁内角的意义。
2、会在简单的图形中辨认同位角、内错角、同旁内角。
3、会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算。
<-)学悄分析:初一学生处于规范阶段,是形象思维向抽象思维过渡的阶段,但学习时精力不够集中,数形结合思想有所欠缺,可学生仍对形象生动、形式多样的学习很有兴趣,在已经学习了内错角的悄况下教师更应积极引导学生树立正确的学习观, 培养其观察力抽象思维能力。
(三)教学重点、难点:教学重点:同位角、内错角、同旁内角的概念。
教学难点:已知两个角,要判别是哪两条直线被第3条直线所截而形成的什么位置关系的角,弄清是哪两条直线被第三条直线所截而成的同位角.内错角、同旁内角。
各对关系角的辨认,复杂图形的辨认是本节教学的难点。
掌握同位角、内错角、同旁内角的相关概念是进一步学习平行线、四边形等后续知识的基础.(四)教法学法:教法:启发式、讨论式、诱思探究的教学方法。
运用基本图形结构将所学的知识及其内在联系向学生展示,启发学生通过主动观察.主动思考、自主探究来达到对知识的发现和接受。
学法:通过老师的引入,结合图像定义从思考题目中理解掌握知识。
这个年龄段的学生思维活跃,求知欲强,但在思维习惯上还有待教师引导,从学生原有的知识和能力出发,教师将带领学生创设疑问,通过合作交流、共同探索来寻求解决问题的方法。
(五)教学过程:1.复习上节内容,创设悄境,引入新概念(PPT第二张):首先我们先回顾一下上节课的内容,分别请儿位学生回答一下PPT 上的问题复习(快速回答): <失《字生上节內吝>1 •平面上两直线间有哪几种关系?3•如图你能找到哪些角角关系?设億图:再提问还有哪些角关系山此引出本课内容。
2•定义(PPT 第三张):观家风筝,我们会发现它是由几根木条交叉 绢成,研究角关系时我们也时當用到形似风筝骨 架的如下图形,那么如何描述如图宜线关系?R 两iT •线被第〔糸血线所我再通过三种形似字母学习相应内容(PPT 第四到七张):同位角► F 形 内错角 Z 形 同旁内角U 形平行或相交2•两直线与第三条直线相交有几个角? 三线八角 对顶角Z1=Z4 , Z5=Z8 ,Z2=Z3Z6=Z7\\3.三线八角:-截线设计总图:利用形似的英文大写字母方便学生记忆本节内容。
1.1 同位角内错角同旁内角

图形特征:在形如“ 的图形中有内错角 的图形中有内错角。 图形特征:在形如“Z”的图形中有内错角。
观察
E
2 3 1
问题3:观察∠ 与 问题 :观察∠4与∠5的位置关系 的位置关系
在直线EF的同旁 ①在直线 的同旁 在直线AB、 的之间 ②在直线 、CD的之间
同旁内角: 同旁内角:
B
4 4 5 7 8 5
同位角、内错角和同旁内角的结构特征: 同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同旁 两旁 同旁 被截线 同侧 之间 之间 结构特征
同位角 内错角 同旁内角
F Z U
课堂练习
1 2 (1)
同位角
识别哪些角是同位角、内错角、 同旁内角。
1 1 (4)
同位角
例2
如图:直线 交 如图:直线DE交∠ABC的 边 的 BA于点 F. 如果内错角∠1与∠2相等, 相等, 于点 如果内错角∠ 与 相等 那么同位角∠ 与 相等, 那么同位角∠1与∠4相等,同旁内角 相等 互补。 ∠1与∠3互补。请说明理由。 与 互补 请说明理由。
A D
2
F
3
4
E
1
B
C
课内练习
1.平面上两条直线有哪两 平面上两条直线有哪两 种位置关系? 种位置关系
(平行和相交) 平行和相交)
2.两条直线相交有几个角 两条直线相交有几个角?
(4个) 个
3. 这4个角的有什么关系吗? 个角的有什么关系吗? 个角的有什么关系吗 4.两条直线与第三条直线相交呢? 8个) ( 个 2 3 6 7 5.这8个角有什么关系呢 个角有什么关系呢? 个角有什么关系呢 8 5
同位角、内错角、同旁内角 1
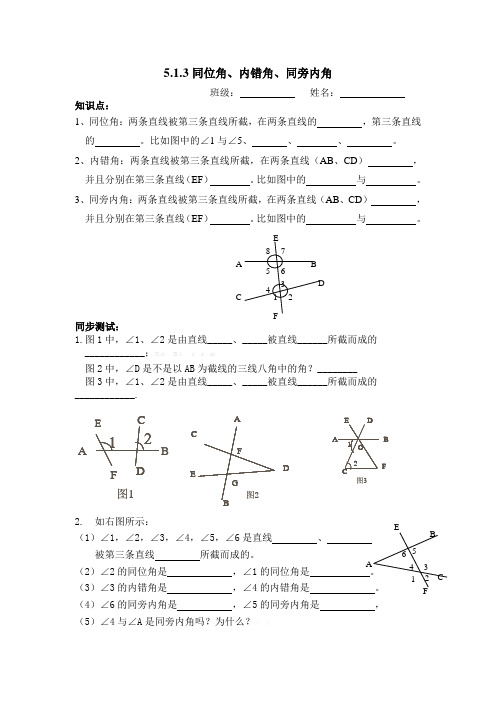
图1B 12A E FC DA BCDEF G图25.1.3同位角、内错角、同旁内角班级: 姓名: 知识点:1、同位角:两条直线被第三条直线所截,在两条直线的 ,第三条直线的 。
比如图中的∠1与∠5、 、 、 。
2、内错角:两条直线被第三条直线所截,在两条直线(AB 、CD ) ,并且分别在第三条直线(EF ) 。
比如图中的 与 。
3、同旁内角:两条直线被第三条直线所截,在两条直线(AB 、CD ) ,并且分别在第三条直线(EF ) 。
比如图中的 与 。
同步测试:1.图1中,∠1、∠2是由直线_____、_____被直线______所截而成的____________;X k B 1 . c o m图2中,∠D 是不是以AB 为截线的三线八角中的角?________ 图3中,∠1、∠2是由直线_____、_____被直线______所截而成的____________.2. 如右图所示:(1)∠1,∠2,∠3,∠4,∠5,∠6被第三条直线 所截而成的。
(2)∠2的同位角是 ,∠1(3)∠3的内错角是 ,∠4的内错角是 。
(4)∠6的同旁内角是 ,∠5的同旁内角是 , (5)∠4与∠A 是同旁内角吗?为什么?3.如图5-1-50,∠2和∠2是____角,∠2与∠4是____∠,∠2与∠8是_____角,∠2与∠6是______角.图5-1-5012345687图5-1-5113121110912345687DCBA图5-1-5243214.如图5-1-51,图中的内错角共有_______对.5.如图5-1-52,∠1与∠2是_____角,∠3与∠4是_____角.6.如图5-1-56,三条直线l1,l2,l3两两相交,则图中共有_____对对顶角,_____对邻补角,_______对同位角,_______对同旁内角,______对内错角.图5-1-56l 3l 2l 114.5163,,130,270,3.AB CD EF --∠=︒∠=︒∠如图所示三条直线、、交于一点若求的度数AECDFB 图5-1-632135.1.3同位角、内错角、同旁内角练习题(2)班级: 姓名: 知识点:1、同位角:两条直线被第三条直线所截,在两条直线的 ,第三条直线的 。
同位角内错角同旁内角的概念区别和联系

同位角内错角同旁内角的概念区别和联系1. 引言概述:同位角内错角和同旁内角是平面几何中的重要概念,它们在解决角度关系问题时起着关键作用。
同位角内错角指的是处于平行线之间,同旁内角则是指两条穿过平行线的直线所形成的内部角。
本文将详细介绍同位角内错角和同旁内角的定义、性质以及它们之间的联系和区别。
文章结构:本文主要包括以下几个部分:引言、同位角的概念、内错角的概念、同旁内角的概念及关系以及总结与展望。
首先,我们将对同位角和内错角进行定义并介绍它们的特点和性质。
接下来,我们将探讨同旁内角的定义,并研究不同情况下同旁内角之间的关系。
最后,我们将总结所发现的重点,并展望未来可能的研究方向。
目的:本文旨在全面阐述同位角内错角和同旁内角这两个重要概念,并探索它们之间的区别和联系。
通过深入剖析其定义与性质以及实际应用示例,读者能够更好地理解这些概念在解决角度问题时的应用。
同时,本文也希望能够为未来相关研究提供一定的启示和方向。
致力于大纲中所给目录,本文将首先概述同位角内错角和同旁内角的整体框架,并明确文章结构。
接下来,我们将详细介绍同位角的定义与特点、性质以及举例说明。
然后,我们将深入探讨内错角的定义、性质和实际应用示例。
之后,我们将专注于同旁内角的定义并研究它们之间的关系。
最后,我们将总结所得,并对未来可能的研究方向进行展望。
通过阅读本文,读者将能够对同位角内错角和同旁内角有一个全面而清晰的认识,并能够准确理解它们在平面几何中的重要作用。
2. 同位角的概念:2.1 定义与特点:同位角是指两条平行线被一条截线所交,所形成的内角对。
这两个内角分别位于截线的同一侧,并且它们互为补角。
换句话说,同位角的和等于180度。
同位角具有以下特点:- 同位角都是内角,在两条平行线之间。
- 同位角相互补充,即一个角加上另一个角等于180度。
- 若直线与多组平行线相交,则同位角可以有多对。
2.2 同位角的性质:同位角满足以下性质:- 垂直定理: 若两条直线被一条截线所交,并且其中两个同位角是垂直的(即互为90度),则这两条直线必定是垂直的。
华东师大版七年级数学上册第5章第1节同位角、内错角、同旁内角
两条直线被第三条直线所截而成的角?
4
E
D
2 C
5
F
展示评价分工表
题号 (1)
(2)
(3)
展示 第一组
第三组
第五组
评价 第二组
第四组
第六组
要求
展示要求: 字迹工整, 排版整齐。
评价要求: 仪态大方, 声音洪亮,
吐字清晰, 指出优点, 补充不足。
解:(1)∠1与∠2是同位角,
A
它们是直线AB、DE被直线
区别:它们位置特征和结构特征都不一样。
联系:1.同位角和同旁内角都在截线的同侧,同旁内 角和内错角都在被截线内部,这三类角都没有公共顶 点。
例:如图:
A
(1)∠1与∠2是什么关系的角,并说出是哪
两条直线被第三条直线所截而成的角?
(2)∠3与∠4是什么关系的角,并说出是哪 1 两条直线被第三条直线所截而成的角? B (3)∠4与∠5是什么关系的角,并说出是哪 3
角的名称
位置特征
同位角 在两条被截直线同旁, 在截线的同侧
图形结构特 形征如字母“F”
(或倒置)
内错角 在两条被截直线内部, 在截线的两侧(交错)
同旁内角
在两条被截直线内部, 在截线的同侧
形如字母 “Z”
(或反置) 形如字母“U”
二.解疑合探
探究1:同位角、内错角、同旁内角它们之间有哪 些区别和联系?
是同旁
∠2与
∠1
是内错角.
课堂小结
1.回想一下预设的问题都解决了吗? 2.学习了本节课内容,你有哪些收获?
学科班长总结:
作业
1、完成课本168页练习1.2题。 2、课本第168页习题5.1。
同位角、内错角、同旁内角(课件ppt)
l
b l
b
新知导入 三线八角
l
P a
b
Q
l
2 1
a
3 4
6
b
5 7
8
从数量关系上看,对顶角相等,相邻的角互补。除此之外, 这八个角还存在什么关系呢?
新知讲解 三线八角
l
2
1
a
3 4
6
b
5 7
8
∠1与∠5的位置有什么关系呢?
(1)从直线l来看,∠1与∠5处于哪个位置? (2)从直线a、b来看,∠1与∠5又处于哪 个位置?
l
a b
三条线交于一点 会出现很多的对 顶角哦
新知导入
如果三条直线相交,可以得到哪些情况? (2)三条直线交于两点,有两条直线平行,且被第三条直线所截;
l b
a
新知导入
如果三条直线相交,可以得到哪些情况? (3)三条直线交于三点,即三条直线两两相交。
l
a b
新知导入
三条直线相交,可以得到两种情况: (1)三条直线交于一点; a
5.1.3同位角、内错角、同旁内角
华东师大版 七年级上
新知导入
两条直线相交,可以得到四个角。下图中的四个角分别是什么关系?
12
a
3 4
b
对顶角: ∠1=∠3,∠2=∠4 互补角: ∠1与∠2,∠2与∠3 ∠3与∠4,∠4与∠1
新知导入
如果三条直线相交,可以得到哪些情况? (1)三条直线交于一点;
1 2 35 4
课堂总结
1、同位角:在两条被截线的同一方,截线的同一侧。 2、内错角:在两条被截线的内部,截线的两侧。 3、同旁内角:在两条被截线的内部,截线的同旁。
10[1].1同位角内错角同旁内角_课件pp
观察 如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
A C
被截直线
截线
E
21
B
34
65
78 D
F
观察 问题:1、观察∠1与∠5的位置关系
同E2 位1 角:①②B在在直直线线AEBF、的C同D的旁同一侧
A
34
1
65
C
78 D
5
F
图形特征:在形如“F”的图形中有同位角。 图中的同位角还有哪些?∠2和∠6;∠3和∠7;
∠4和∠8
1 探索交流 变式图形:图中的∠1与∠2都是同位角。
在形如字母“F”的图形中有同位角。
观察 问题:2、观察∠3与∠5的位置关系
内错角:①在直线EF的两侧
②在直线AB、CD的之间
E
21
B
A
34
65
3 5
C
78 D
图形特征:在形F如“Z”的图形中有内错角。
图中的内错角还有哪些? ∠4和∠6
BC所截构成的__同__位__角。
注意:
上述三类角类似于对应角都是成对出现。 不能说哪个角是同位角、内错角等?
例1 如图,直线DE截AB,AC,构成8个角。
指出所有的同位角、内错角和同旁内角。 A
D
2 1
3
4
B
温馨提示:
58
67 E
C
解题之前要明确哪两条直线被哪条直线所截
变式: A
D
2 1
3
4
B
58
67 E
C
如果是AB与DE 被AC所截, 请指出其中的同位角、内错角、同旁内角?
同位角、内错角、同旁内角(不分层)知识讲解
同位角、内错角、同旁内角知识讲解责编:康红梅【学习目标】1.了解“三线八角”模型特征;2.掌握同位角、内错角、同旁内角的概念,并能从图形中识别它们.【要点梳理】要点一、同位角、内错角、同旁内角的概念1. “三线八角”模型如图,直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截),构成八个角,简称为“三线八角”,如图1.图1要点诠释:⑴两条直线AB,CD与同一条直线EF相交.⑵“三线八角”中的每个角是由截线与一条被截线相交而成.2. 同位角、内错角、同旁内角的定义在“三线八角”中,如上图1,(1)同位角:像∠1与∠5,这两个角分别在直线AB、CD的同一方,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同位角.(2)内错角:像∠3与∠5,这两个角都在直线AB、CD之间,并且在直线EF的两侧,像这样的一对角叫做内错角.(3)同旁内角:像∠3和∠6都在直线AB、CD之间,并且在直线EF的同一旁,像这样的一对角叫做同旁内角.要点诠释:(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系,显然是没有公共顶点的两个角.(2)“三线八角”中共有4对同位角,2对内错角,2对同旁内角.【高清课堂:平行线及其判定403102三线八角】要点二、同位角、内错角、同旁内角位置特征及形状特征要点诠释:巧妙识别三线八角的两种方法:(1)巧记口诀来识别:一看三线,二找截线,三查位置来分辨.(2)借助方位来识别根据这三种角的位置关系,我们可以在图形中标出方位,判断时依方位来识别,如图2.【典型例题】类型一、“三线八角”模型1.(1)图3中,∠1、∠2由直线被直线所截而成.(2)图4中,AB为截线,∠D是否属于以AB为截线的三线八角图形中的角?【答案】(1) EF,CD; AB.(2)不是.【解析】(1)∠1、∠2两角共同的边所在的直线为截线,而另一边所在的直线为被截线.(2)因为∠D的两边都不在直线AB上,所以∠D不属于以AB为截线的三线八角图形中的角.【总结升华】判断“三线八角”的关键是找出哪两条直线是被截线,哪条直线是截线.类型二、同位角、内错角、同旁内角的辨别2.如图,(1)DE为截线,∠E与哪个角是同位角?(2)∠B与∠4是同旁内角,则截出这两个角的截线与被截线是哪些直线?(3)∠B和∠E是同位角吗?为什么?【答案与解析】解:(1)DE为截线,∠E与∠3是同位角;(2)截出这两个角的截线是直线BC,被截线是直线BF、DE;(3)不是,因为∠B与∠E的两边中任一边没有落在同一直线上,所以∠B和∠E不是同位角.【总结升华】确定角的关系的方法:(1)先找出截线,由截线与其它线相交得到的角有哪几个;(2)将这几个角抽出来,观察分析它们的位置关系;(3)再取其它的线为截线,再抽取与该截线相关的角来分析.举一反三:【变式】(2016春•邹城市校级期中)如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角【答案】B解:从图上可以看出∠1和∠5不存在直接联系,而其它三个选项都符合各自角的定义,正确.3.(2014秋•太康县期末)如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.【答案与解析】解:内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5;同位角:∠3与∠7,∠2与∠8,∠4与∠6.【总结升华】要分析各对角是由哪两条直线被哪一条直线所截的,可以把复杂图形按题目要求分解成简单的图形后,结论便一目了然.举一反三:【变式】如图∠1、∠2、∠3、∠4、∠5中,哪些是同位角?哪些是内错角?哪些是同旁内角?【答案】解:同位角:∠5与∠1,∠4与∠3;内错角:∠2与∠3,∠4与∠1;同旁内角:∠4与∠2,∠5与∠3,∠5与∠4.【高清课堂:平行线及其判定403102三线八角练习(2)】4. 分别指出下列图中的同位角、内错角、同旁内角.【答案与解析】解:同位角:∠B与∠ACD,∠B与∠ECD;内错角:∠A与∠ACD,∠A与∠ACE;同旁内角:∠B与∠ACB,∠A与∠B,∠A与∠ACB,∠B与∠BCE.【总结升华】在复杂图形中,分析同位角、内错角、同旁内角,应把图形分解成几个“两条直线与同一条直线相交”的图形,并抽取交点处的角来分析.举一反三:【变式】请写出图中的同位角、内错角、同旁内角.【答案】解:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8是同位角;∠2与∠8,∠3与∠5是内错角;∠2与∠5,∠3与∠8是同旁内角.类型三、同位角、内错角、同旁内角大小之间的关系5. 如图直线DE、BC被直线AB所截,(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?每组中两角的大小关系如何?(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?【答案与解析】解:(1)∠1和∠2是内错角;∠1和∠3是同旁内角;∠1和∠4是同位角.每组中两角的大小均不确定.(2) ∠1与∠2相等,∠1和∠3互补. 理由如下:①∵∠1=∠4(已知)∠4=∠2(对顶角相等)∴∠1=∠2.②∵∠4+∠3=180°(邻补角定义)∠1=∠4(已知)∴∠1+∠3=180°即∠1和∠3互补.综上,如果∠1=∠4,那么∠1与∠2相等,∠1和∠3互补.【总结升华】在“三线八角”中,如果有一对同位角相等,则其他对同位角也分别相等,并且所有的内错角相等,所有同旁内角互补.举一反三:【变式1】若∠1与∠2是内错角,则它们之间的关系是 ( ) .A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.∠1=∠2或∠1>∠2或∠1<∠2【答案】D【变式2】下列命题:①两条直线相交,一角的两邻补角相等,则这两条直线垂直;②两条直线相交,一角与其邻补角相等,则这两条直线垂直;③内错角相等,则它们的角平分线互相垂直;④同旁内角互补,则它们的角平分线互相垂直,其中正确的个数为().A.4 B.3 C.2 D.1 【答案】C (提示:②④正确).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学下册
湛江一中培才学校肖海涛
C
D
E
F
12
431直线CD 和EF 相交所形成的角有哪些关系?
具
有对顶角关系的角
对等角相等。
直线CD 和EF 相交所形成的角有哪些关系?
2
1414C
D
E
F
3具有邻补角关系的角
邻补角互补
两条直线AB 和CD 被第三条直线EF 所截成的角共有几个?
直线AB 、CD----被截直线78
56
4132
C D
A
B
答:8个(一般称为三线八角)
直线EF----截线
F
E
下面四个角是不共顶点的,这节课我们要学习其中没有公共顶点的两个角
之间的位置关系。
854
1
2
67
3A
B
C
D
E
5
1各有一边在同一直线上(这条直线是截线)观察∠1和∠5两角与截线及被截线的位置关系有何特点:
两个角都在截线的同侧(左侧)两个角都在被截线的同一方(下方)
7
842
63A
B
C
D
E
F
5
1
两个角都在截线同侧,且两个角都在被截线的同一方;
同位角
观察∠1和∠5两角与截线及被截线的位置关系有何特点:
如∠1与∠5都在截线的左侧,在被截
直线的下方
51
2
67
384图中的同位角除∠1和∠5外,还有……
下列哪些图形中的∠1与∠2是同位角?
1
2
(1)
1
2
(2)1
2
(3)
1 2
(4)
×
是
×是基础练习1:
8
4
126 7
观察∠3和∠5两角与截线及被截线的位置关系有何特点:
5
3
各有一边在同一直线上(截线)
5
3
84
1
2
67
53
两个角分别在截线的两侧
5
3
8
4
1
2
67
53
两个角都夹在两被截直线之内
5
3
8
4
1
2
6753
两个角分别在截线的
两侧,两个角夹在两
被截直线之内;
内错角5
3
观察∠3和∠5两角与截线及被截线
的位置关系有何特点:
夹在两被截直线
内,分别在截线
两侧(交错)
7
81
2
5346图中的内错角除∠3和∠5外,还有……
1)如图,直线AD 、BC 被直线AC 所截,找出图中由AD 、BC 被直线AC 所截而成的内错角是和。
(2)∠3和∠4是直线和被所截,构成内错角。
∠1∠2AB DC AC 基础练习2:
A
C 1
2D
34
B
E
7
854
1
2
观察∠3和∠6两角与截线及被截线的位置关系有何特点:
36
两角各有一边在同一直线上(截线)
3
6观察∠3和∠6两角与截线及被截线的位置关系有何特点:
8
4
1
2
6753
两个角在截线的同一侧(右侧)
3
6841
2
67
53
两个角都夹在两被截直线之内
3
6841
2
67
53
两个角在截线的同一侧(右侧),两个角都夹在两被截直线之内
同旁内角
3
6观察∠3和∠6两角与截线及被截线的位置关系有何特点:
在截线同旁,夹
在两被截直线内
7
81
2
5436图中的同旁内角除∠3和∠6外,还有……
形如字母“U”
在两条被截直线之内,
在截线同侧
同旁内角
形如字母“Z”(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”(或倒置)在两条被截直线同一方,在截线同侧同位角
图形结构特征位置特征角的名称
试一试:
请同学们分别用双手的大拇指,食指各组成一个角,两食指相对成一条线,保持在同一平面内,分别进行尝试,看可以组成哪些角。
AB所截,
(1)∠1和∠2、∠1和∠3、∠1
和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和
∠2相等吗?∠1和∠3互补吗
?为什么?
D E
C
B
2
4
3
1
AB所截,
(1)∠1和∠2、∠1和∠3、∠1
和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和
∠2相等吗?∠1和∠3互补吗
?为什么?
D E
C
B
2
4
3
1
(1)∠1和∠2是内错角;∠1和∠3是同旁内角;
∠1和∠4是同位角。
(2)∵∠1=∠4(已知)
∠4=∠2 (对顶角相等)
∴∠1=∠2.
∵∠4+∠3=180°(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3=180°
即∠1和∠3互补.
答:
a 8
5
2
1
6c
b
课时练习:
1、(1)找出图中的同位角、内错角、同旁内角:
变式:找出图中的同位角、内错角、同旁内角:
a
b
1
5
c
324
c
b a
(2)找出图中的同位角、内错角、同旁内角:
2
2、如图∠1与哪个角是内错角,与哪个角是同旁内角?∠2与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所形成的?
1)图中,与哪个角是内错角?与哪个角是同旁内角?它们分别是有哪两条直线被哪一条直线截成的?
1∠1∠D A E
B C
1
2
图中与∠1是同旁内角的角它们分别是有哪两条直线被哪一条直线截成的?
(2)图中∠2的内错角的角它们分别是有哪两条直线被哪一条直线截成的?
2
图中∠2的同旁内角的角它们分别是有哪两条直线被哪一条直线截成的?
2
说能出你这节课的收获和体验让大家与你分享吗?
形如字母“U”在两条被截直线之内,在截线同侧同旁内角形如字母“Z”(或反置)在两条被截直线之内,
在截线两侧(交错)
内错角形如字母“F”(或倒置)在两条被截直线同
一方,在截线同侧
同位角图形结构特征位置特征
角的名称1、这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
课时小结
2、同位角、内错角、同旁内角的特点:
课后补充习题。
