三种抽样方法(全)
随机抽样(必修3)(三种抽样方法)

(3)在第1段用简单随机抽样确定第一个个体编 号m(m≤k)
(4)按照一定的规则抽取样本。通常是将m加上 间隔k得到第二个个体编号(m+k),再加k得 到第3个个体编号,依次进行下去,直到获得整 个样本。
思考:
当N/n不是整数时,如何进行 系统抽样?
当N/n不是整数时,令k=[N/n],那先从总 体中用简单随机抽样的方法剔除N-nk个个体, 再将其余的进行编号并均分成n段(可知每段 间隔数为K)。
1分层抽样
(1)定义一:一般地,在抽样时,将总体分成互不交叉 的层,然后按照一定的比例,从各层独立地抽取一定 数量的个体,将各层取出的个体合在一起作为样本, 这种抽样的方法叫分层抽样。
系统抽样(等距抽样)的概念 将总体分成均衡的几部分,然后按照预先定出的
规则,从每一个部分抽取一个个体,得到所需样本的 抽样方法叫做系统抽样。
系统抽样的特点
(1)适用于总体容量较大的情况;
(2)剔除多余个体及第一段抽样都用简单随机抽样, 因而与简单随机抽样有密切联系;
(3)是等可能抽样,每个个体被抽到的可能性都 是n/N;
(4)是不放回的抽样。
合理选择抽样方法
系统抽样 简单 抽签法 随机 抽样 随机数
表法
总体容量
很大
较小
样本容量 较大
较小
较大
较大
下页
练习:要从1002个学生中选 取一个容量为20的样本,试 用系统抽样的方法给出抽样 过程。
2.1.3分层抽样
情景设置
问题1 :要抽样了解某年参加高考学生的语文成绩,我 们可以有以下两种抽样的方式; (1)从所有考生中用简单随机抽样的方法抽取1000份试 卷做调查; (2) 分文科,理科,艺术,体育等科目类的学生适当比例 抽取样本容量为1000的的样本,再做调查.
考点29 三种抽样方法(讲解) (原卷版)
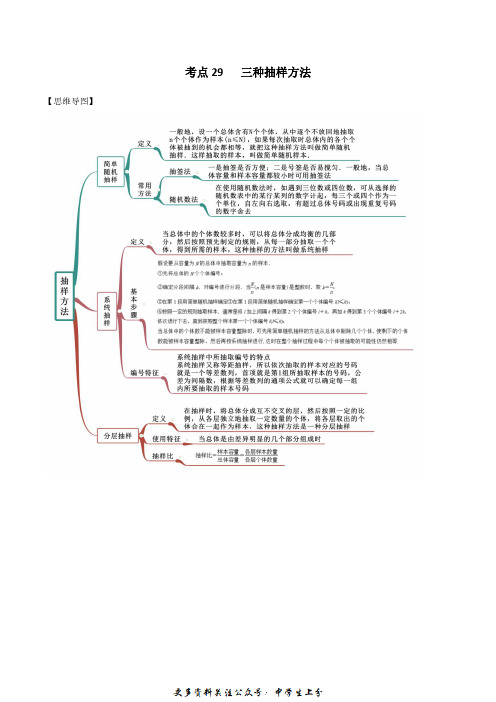
考点29三种抽样方法【思维导图】【常见考法】考法一简单随机抽样1.总体由编号为01,02,…,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为()50446644216606580562616554350242354896321452415248 22662215862663754199584236722458375218510337183911A.23B.21C.35D.322.某口罩生产工厂为了了解口罩的质量,现将生产的50个口罩编号为01,02,…,50,利用如下随机数表从中抽取10个进行检测.若从下表中第1行第7列的数字开始向右依次读取2个数据作为1个编号,则被抽取的第8个个体的编号为()72847114351911584926501117177686315720189560784675 88782816841352539453754569309673896570319914434876 A.18B.50C.11D.17考法二系统抽样1.某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是A.8号学生B.200号学生C.616号学生D.815号学生2.某班有学生60人,现将所有学生按1,2,3,…,60随机编号,若采用系统抽样的方法抽取一个容量为5的样本(等距抽样),已知编号为4,,28,,52a b 号学生在样本中,则a b +=()A.42B.45C.52D.563.从编号0,1,2,…,79的80件产品中,采用系统抽样的方法抽取容量是10的样本,若编号为58的产品在样本中,则该样本中产品的最大编号为()A.72B.74C.76D.78考法三分层抽样1.某高中学校三个年级共有学生2800名,需要用分层抽样的方法抽取一个容量为40的样本,已知高一年级有学生910名,高二年级抽出的样本人数占样本总数的310,则抽出的样本中有高三年级学生人数为()A.14B.15C.16D.172.某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n 的样本,已知从高中生中抽取70人,则n 为()A.100B.150C.200D.2503.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从乙车间的产品中抽取了4件,则n ()A.9B.10C.12D.134.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是()A.12,24,15,9B.9,12,12,7C.8,15,12,5D.8,16,10,6。
三种抽样方法(全)

8
【例题解析】 例1、某校高中三年级的295名学生已经编 号为1,2,……,295,为了了解学生的学习情 况,要按1:5的比例抽取一个样本,用系统抽 样的方法进行抽取,并写出过程。 解:样本容量为295÷5=59.
确定分段间隔k=5,将编号分段 1~5,6~10,…,291~295; 采用简单随机抽样的方法,从第一组5名 学生中抽出一名学生,如确定编号为3的学生, 依次取出的学生编号为3,8,13,…,288,293 , 这样就得到一个样本容量为59的样本.
24
※(2004年福建省高考卷)一个总体中有 100个个体,随机编号为0,1,2,…,99,依编号顺序 平均分成10个小组,组号分别为1,2,3,…,10.现 用系统抽样方法抽取一个容量为10的样本,规 定如果在第1组随机抽取的号码为m,那么在第k 组抽取的号码个位数字与m+k的个位数字相同. 若m=6,则在第7组中抽取的号码是______. 解析:依编号顺序平均分成的10个小组分 别为0~9, 10~19, 20~29, 30~39, 40~49,50~59,60~69,70~79,80~89,90~99.因第 7组抽取的号码个位数字应是3,所以抽取的号码 是63.这个样本的号码依次是 6,18,29,30,41,52,63,74,85,96这10个号. 25
二、分层抽样的步骤: (1)按某种特征将总体分成互不相交的层 (2)按比例k=n/N确定每层抽取个体的个数 (n/N)*Ni个。 (3)各层分别按简单随机抽样的方法抽取。 (4)综合每层抽样,组成样本。 练习:分层抽样又称类型抽样,即将相似的个 体归入一类(层),然后每层抽取若干个体构 成样本,所以分层抽样为保证每个个体等可能 入样,必须进行 (c ) A、每层等可能抽样 B、每层不等可能抽样 16 C、所有层按同一抽样比等可能抽样
三种抽样方法

等可能 抽取;
不放回 抽取;
三种抽样方法的应用
1 、统计的根本思想方法是__用__样__本__估__量__总__体__. 抽样调查常用的方法有_简__洁__随__机__抽__样__,_系__统__抽__样__,分__层__抽__样__. 样本容量是指__样__本__中__包__含__的__个__体__的__个__数__.
解:抽取人数与职工总数的比是100:500=1:5 ,则各年 龄段〔层〕的职工人数依次是125: 280:95=25:56:19,然后分别在各年龄段〔 层〕运用简洁随机抽样方法抽取.
答:在分层抽样时,不到35岁、35~49岁、50岁 以上的三 个年龄段分别抽取25人、56人和19人.
4.三种抽样方法的比较
类别 简单随机
抽样
系统 抽样
分层 抽样
各自特点
从总体中 逐个抽取
将总体均分成 几局部,按事 先确定的规章 在各局部抽取
将总体分成 几层,分层 进展抽取
相互联系 适用范围 共同点
在起始局部 抽样时承受 简洁随机抽
样
各层抽样时 承受简洁随 机抽样或系 统抽样
总体中的 个体数较
少
总体中的 个体数较
多
总体由差 异明显的 几局部组
A.方法2,方法1,方法3
B.方法2,方法3,方法1
C.方法1,方法2,方法3
D.方法3,方法1,方法2
Hale Waihona Puke 总结• 在现实生活中,由于资金、时间有限 人力、物力缺乏,再加上不断变化的 环境条件,做普查是不行能的。所以 在现实抽样中,为了使样本具有代表 性,通常要同时使用几种抽样方法.这 和做人的道理是全都的,这就是数学 的哲学美!
法一:首先,把该校学生都编上号码:0001,0002,0003,…,1200.如用 抽签法,则作1200个外形、大小一样的号签〔号签可以用小球、卡片、纸条 等制作〕,然后将这些号签放在同一个箱子里,进展均匀搅拌.抽签时,每 次从中抽出1个号签,连续抽取50次,就得到一个容量为50的样本. 法二:首先,把该校学生都编上号码:0001,0002,0003,…,1200如用 随机数表法,则可在数表上随机选定一个起始位置,开头向右连续取数字, 以4个数为一组,始终取够50人为止.
抽样方法有些抽样方法大全

抽样方法有些抽样方法大全抽样方法是指从总体中选取一部分样本进行调查或研究的方法。
抽样方法的选择对于研究结果的可靠性和推广性有着重要的影响。
下面是一些常用的抽样方法:1. 简单随机抽样(Simple Random Sampling):在总体中的每个个体具有相同的被选中的机会,通过随机抽取样本来代表总体。
2. 分层抽样(Stratified Sampling):将总体分成若干层次,每一层次中的个体具有相似的特征,然后从每个层次中随机抽取样本。
3. 整群抽样(Cluster Sampling):将总体划分为若干个群组,然后通过随机抽取部分群组来代表总体,然后在所选的群组中进行全面调查。
4. 系统抽样(Systematic Sampling):根据固定的抽样间隔,从总体中随机选择一个起始点,然后按照固定的间隔依次选取样本。
5. 多阶段抽样(Multistage Sampling):将总体分层和分群组,然后通过多个抽样阶段来实现抽样,通常用于大规模调查。
6. 比率抽样(Ratio Sampling):根据总体中的其中一特征的比例,确定样本的大小。
例如,如果总体中男性比例是60%,则样本中男性比例也应该是60%。
7. 效应抽样(Convenience Sampling):根据研究者的方便或可获得性,选择样本。
这种方法容易产生偏差,结果可能无法推广到整个总体。
8. 整齐抽样(Quota Sampling):根据总体中一些特征的比例,确定样本的大小。
例如,如果总体中男性比例是60%,则样本中男性数量也应该是60%。
9. 小组抽样(Snowball Sampling):从已经选择的样本中获取参与者的指引,逐渐扩大样本规模,并在招募新样本时依靠参与者的推荐。
10. 专家抽样(Expert Sampling):指选择一些具有特定知识、经验或技能的专家作为样本,以获取专业领域的意见或建议。
以上是一些常用的抽样方法,每种方法都有其适用的场景和限制,研究者需要根据研究目的、总体特征、样本大小和可行性等因素综合考虑选择最合适的抽样方法。
三种抽样方案
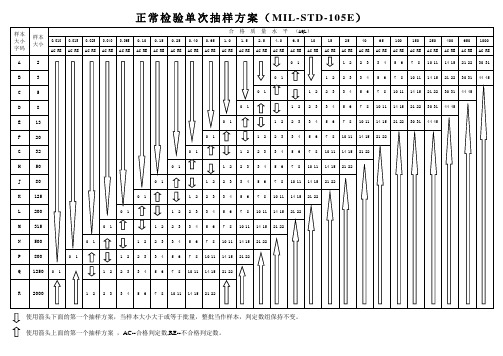
正常检验单次抽样方案(MIL-STD-105E)
使用箭头下面的第一个抽样方案,当样本大小大于或等于批量,整批当作样本,判定数组保持不变。
使用箭头上面的第一个抽样方案,AC--合格判定数,RE--不合格判定数。
正常检验单次抽样方案(MIL-STD-105E)
使用箭头下面的第一个抽样方案,当样本大小大于或等于批量时,整批当作样本,判定数组保持不变。
使用箭头上面的第一个抽样方案 ,AC--合格判定数,RE--不合格判定数。
使用箭头下面的第一个抽样方案,当样本大小大于或等于批量时,整批当作样本,判定数组保持不变。
使用箭头上面的第一个抽样方案 ,AC--合格判定数,RE--不合格判定数。
样本大小字码。
信息传播中内容分析的三种抽样方法

1999年第3期 图书情报知识 1999年9月信息传播中内容分析的三种抽样方法任学宾(广西教育学院图书馆,南宁,530023) [摘要] 在信息传播研究中,内容分析法占有重要的地位。
本文对目前国外常用的报纸内容分析的抽样方法作了简要介绍。
[关键词] 报纸 内容分析 抽样方法1 引言内容分析法是信息传播研究中的基本方法之一,它对传播内容进行客观的、系统的和数量的描述。
由于这种方法可用于各种信息资料的分析,且比一般的文献统计法更能准确地反映客观实际,因而它在信息传播研究中占有重要的地位。
在传播媒介中,报纸具有信息量大、传递及时快捷、时效长、覆盖面广及影响力强等综合优势,是当今公众获取信息的第一信息源,也是情报研究的重要信息源。
近年来,对报纸内容进行分析日益受到人们的重视。
我国读者首先是通过美国学者奈斯比特的《大趋势》一书接触到内容分析法的。
目前,运用这种方法进行社会研究的还不多,对报纸内容进行分析的更是“凤毛麟角”。
这种现象的出现,与我国的有关著作中对该方法的介绍比较粗略及缺少实用的操作方法有关。
例如,对决定分析深度与工作效率的关键步骤——“选择样本”的介绍,大多数有关的著作只对全样调查法作了介绍,而对国外比较流行的抽样调查法却较少提及,少数有关著作虽然介绍了抽样调查法,但也只是点到为止,缺少具体的操作指导。
本文拟对报纸内容分析的抽样方法作些介绍,供有关人员参考。
2 三种抽样方法简介目前,国外对报纸进行内容分析的常用抽样方法有三种,即简单随机抽样(si m p le random sam p le)、构造周抽样(con structed w eek o r com po site w eek sam p le)和连续日期抽样(con secu tive day sam p le)。
(1)简单随机抽样法。
它是严格按照随机原则对总体进行抽样的方法。
我国读者对这种方法比较熟悉,在一般的“数理统计”方面的著作中对它均有介绍,笔者不再赘述。
大数据时代如何“以偏概全”——三种常见抽样方法的简单辨析

最 常见 的简 单 随 机 抽 样 的方 法 就 是 我 骤 进 行 : 们 日常生 活 中经 常 采 用 的“ 抓 阄” 法. 例如, 某学校高 一年 级数 学 兴趣 小 组有 1 2名 组 员, 现要从 中选 出 2名 组 员 参 加 区级 数 学 竞 第一 步 , 先将 4 0件 产 品编 号 , 可 以 编 为
一
号一 致 的样本 抽 出.
、
简 单 随 机 抽 样 — — 所 有 抽
当遇 到 总体 的个 体 数 比较 多 的 时候 , 我
们可 以通 过制 作 一 个 数 表来 代 替 号签 , 表 中 的每 一个 数都 是 用 随 机 方 法 产 生 的 , 这样 的
样 方 法 的 基 础
一
般地 , 从元 素个 数 为 N 的总体 中不 放 表 称 为 随 机 数 表 .
抽签 法从 个 体 数 为 N 的 总 体 中抽 取 一 个 容 行 摘 录 如 下 .
第 三步 , 从 选 定 的 数 5开 始 向 右 读 下 将 它去掉 ; 继 续 向右 读 , 得到 1 6 , 将它取 出;
去, 得 到一个 两位 数字 号 码 5 9 , 由于 5 9  ̄3 9 , 继续 下 去 , 又得到 1 9 , 1 0 , 1 2 , 0 7 , 3 9 , 3 8 , 3 3 ,
况, 可 先将 总 体 中各 个 个 体 按 差 别 特 征 , 分 线 上 的所有 产 品进 行 抽 取样 本 . 因 为 1个 小 成 层次 分 明且互 不 重 叠 的几 部 分 , 然 后按 各 时 内流 水线 上能 生产 出 4组 产 品 , 每 组有 1 O 部 分在 总体 中所 占 比例 进 行 抽 样 , 这 种抽 样 件 , 所 以我 们 可 以 在 第 一 个 1 5分 钟 内的 这 方 法 叫作分 层抽 样 , 其 中所 分 成 的各 个 部 分 组 中采 用简 单 随机 抽 样 抽 取 一个 样 本 , 并 记
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
【例题解析】 例1、某校高中三年级的295名学生已经编 号为1,2,……,295,为了了解学生的学习情 况,要按1:5的比例抽取一个样本,用系统抽 样的方法进行抽取,并写出过程。 解:样本容量为295÷5=59.
确定分段间隔k=5,将编号分段 1~5,6~10,…,291~295; 采用简单随机抽样的方法,从第一组5名 学生中抽出一名学生,如确定编号为3的学生, 依次取出的学生编号为3,8,13,…,288,293 , 这样就得到一个样本容量为59的样本.
24
※(2004年福建省高考卷)一个总体中有 100个个体,随机编号为0,1,2,…,99,依编号顺序 平均分成10个小组,组号分别为1,2,3,…,10.现 用系统抽样方法抽取一个容量为10的样本,规 定如果在第1组随机抽取的号码为m,那么在第k 组抽取的号码个位数字与m+k的个位数字相同. 若m=6,则在第7组中抽取的号码是______. 解析:依编号顺序平均分成的10个小组分 别为0~9, 10~19, 20~29, 30~39, 40~49,50~59,60~69,70~79,80~89,90~99.因第 7组抽取的号码个位数字应是3,所以抽取的号码 是63.这个样本的号码依次是 6,18,29,30,41,52,63,74,85,96这10个号. 25
二、分层抽样的步骤: (1)按某种特征将总体分成互不相交的层 (2)按比例k=n/N确定每层抽取个体的个数 (n/N)*Ni个。 (3)各层分别按简单随机抽样的方法抽取。 (4)综合每层抽样,组成样本。 练习:分层抽样又称类型抽样,即将相似的个 体归入一类(层),然后每层抽取若干个体构 成样本,所以分层抽样为保证每个个体等可能 入样,必须进行 (c ) A、每层等可能抽样 B、每层不等可能抽样 16 C、所有层按同一抽样比等可能抽样
17
解:因为疾病与地理位置和水土均有关系,
所以不同乡镇的发病情况差异明显,因而采用 分层抽样的方法,具体过程如下: (1)将3万人分为5层,其中一个乡镇为一层。 (2)按照样本容量的比例随机抽取各乡镇应 抽取的样本。 300×3/15=60(人),300×2/15=100(人), 300×2/15=40(人),300×2/15=60(人), 因此各乡镇抽取人数分别为60人、40人、100人、 40人、60 人。 (3)将300人组到一起,即得到一个样本。
第三步:从号码为1~10的第一个间隔中用简单随机抽样 的方法确定第一个个体编号,假如为6号; 第四步:从第6号开始,每隔10个号码抽取一个,得到 6,16,26,36,…,496.这样就得到一个样本容量为 3 50的样本.
一.系统抽样的定义: 将总体平均分成几部分,然后按照一定的规 则,从每一部分抽取一些个体作为样本,这种抽 样的方法叫做系统抽样。
1
2.1.2 系统抽样
一、学习目标: 1、知识与技能: (1)正确理解系统抽样的概念; (2)掌握系统抽样的一般步骤; (3)正确理解系统抽样与简单随机抽样的关系; 2、过程与方法:通过对实际问题的探究,归纳应用 数学知识解决实际问题的方法,理解分类讨论的数学 方法, 3、情感态度与价值观:通过数学活动,感受数学对 实际生活的需要,体会现实世界和数学知识的联系。 二、重点与难点:正确理解系统抽样的概念,能够灵 活应用系统抽样的方法解决统计问题。
18
课堂小结
一、系统抽样 1.系统ຫໍສະໝຸດ 样的定义;2.系统抽样的一般步骤;
3.分段间隔的确定.
19
二、分层抽样
1 、分层抽样是当总体由差异明显的几部分组成时采 用的抽样方法,进行分层抽样时应注意以下几点: ( 1 )分层抽样中分多少层、如何分层要视具体情况 而定,总的原则是,层内样本的差异要小,面层之间的 样本差异要大,且互不重叠。 ( 2 )为了保证每个个体等可能入样,所有层应采用 同一抽样比等可能抽样。 ( 3 )在每层抽样时,应采用简单随机抽样或系统抽 样的方法进行抽样。 2 、分层抽样的优点是:使样本具有较强的代表性, 并且抽样过程中可综合选用各种抽样方法,因此分层抽 样是一种实用、操作性强、应用比较广泛的抽样方法。 20
10
例3:从2005个编号中抽取20个号码入样,采 用系统抽样的方法,则抽样的间隔为 ( C) A.99 B、99.5
C.100
D、100.5
例4:某小礼堂有25排座位,每排20个座位,一次 心理学讲座,礼堂中坐满了学生,会后为了了解 有关情况,留下座位号是15的所有25名学生进行 测试,这里运用的是 系统 抽样方法。
5
〖说明〗(1)分段间隔的确定:
剔除几个个体,使得总体中剩余的个体数能被样
N 本容量整除.通常取k= n
N N 当 是整数时,取k= ; n n N 当 不是整数时,可以先从总体中随机地 n
(2)从系统抽样的步骤可以看出,系统抽样 是把一个问题划分成若干部分分块解决,从而 把复杂问题简单化,体现了数学转化思想。
11
例5:采用系统抽样从个体数为83的总体中 抽取一个样本容量为10的样本,那么每个个体
10 人样的可能性为 _________. 83
例6:从2004名学生中选取50名组成参观 团,若采用下面的方法选取:先用简单随机抽 样从2004人中剔除4人,剩下的2000个再按系 统抽样的方法进行,则每人入选的机会( C)
二、从容量为N的总体中抽取容量为n的样本,用 系统抽样的一般步骤为: (1)将总体中的N个个体编号.有时可直 接利用个体自身所带的号码,如学号、准考证号、 门牌号等; (2)将编号按间隔k分段(k∈N). (3)在第一段用简单随机抽样确定起始 个体的编号L(L∈N,L≤k)。 (4)按照一定的规则抽取样本,通常是 将起始编号L加上间隔k得到第2个个体编号L+K, 再加上K得到第3个个体编号L+2K,这样继续下 去,直到获取整个样本.
例1、某高中共有900人,其中高一年级300 人,高二年级200人,高三年级400人,现采用 分层抽样抽取容量为45的样本,那么高一、高 二、高三各年级抽取的人数分别为( D ) A.15,5,25 B.15,15,15 C.10,5,30 D15,10,20
例2:一个地区共有5个乡镇,人口3万人, 其中人口比例为3:2:5:2:3,从3万人中抽 取一个300人的样本,分析某种疾病的发病率, 已知这种疾病与不同的地理位置及水土有关, 问应采取什么样的方法?并写出具体过程。
复习
1.简单随机抽样的概念
一般地,设一个总体的个体数为 N ,如果通过逐个 不放回地抽取的方法从中抽取一个样本,且每次抽取时 各个个体被抽到的概率相等,就称这样的抽样为简单随 机抽样。
2.简单随机抽样的方法:
抽签法
随机数表法
注:随机抽样并不是随意或随便抽取,因为随意或
随便抽取都会带有主观或客观的影响因素.
【说明】由系统抽样的定义可知系统抽样有以下特证: (1)当总体容量N较大时,采用系统抽样。 (2)将总体平均分成几部分指的是将总体分段,分段的 间隔要求相等,因此,系统抽样又称等距抽样, 这时间隔一般为k= ([x]表示不超过x的最大整数). (3)一定的规则通常指的是:在第1段内采用简单随机 抽样确定一个起始编号,在此编号的基础上加上分段间 4 隔的整倍数即为抽样编号。
试利用上述资料设计一个抽样比为1/10的抽样方法。
23
练习、在1000个有机会中奖的号码(编号为 000~999)中,在公证部门的监督下,按随机抽 取的方法确定最后两位数为88的号码为中奖号码, 这是运用那种抽样方法确定中奖号码的?依次写 出这10个中奖号码。
系统抽样
088,188,288,388,488,588,688,788, 888,988
3 、某中学高一年级有学生 600 人,高二年级有学生 450人,高三年级有学生 750人,若该校取一个容量为 n 的样本,每个学生被抽到的可能性均为0.2, 则n= 。 4 、对某单位 1000 名职工进行某项专门调查,调查的 项目与职工任职年限有关,人事部门提供了如下资料:
任职年限 人数 5年以下 300 5年至10年 500 10年以上 200
2.1.3 分层抽样
14
一、分层抽样的定义。 一般地,在抽样时,将总体分成互不交叉 的层,然后按照一定的比例,从各层独立地抽 取一定数量的个体,将各层取出的个体合在一 起作为样本,这种抽样的方法叫分层抽样。
应用分层抽样应遵循以下要求: (1)分层:将相似的个体归入一类,即为一层, 分层要求每层的各个个体互不交叉,即遵循不重 复、不遗漏的原则。 (2)分层抽样为保证每个个体等可能入样,需 遵循在各层中进行简单随机抽样,每层样本数量 与每层个体数量的比与这层个体数量与总体容量 15 的比相等。
A.不全相等
C.都相等
B.均不相等
D.无法确定
12
探究?
假设某地区有 高中生2400人,初 近视率% 80 中生10900人,小 学生11000人,此 60 地教育部门为了了 解本地区中小学的 40 近视情况及其形成 20 原因,要从本地区 的小学生中抽取 0 1%的学生进行调 小学 初中 高中 你认为哪些因素影响学生视 查,你认为应当怎 力?抽样要考虑和因素? 样抽取样本? 13
6
思考:下列抽样中不是系统抽样的是 ( C ) A、从标有1~15号的15个小球中任选3个作 为样本,按从小号到大号排序,随机确定起点i, 以后为i+5, i+10(超过15则从1再数起)号入样; B、工厂生产的产品,用传送带将产品送入 包装车间前,检验人员从传送带上每隔五分钟抽 一件产品检验; C、搞某一市场调查,规定在商场门口随机 抽一个人进行询问,直到调查到事先规定的调查 人数为止; D、电影院调查观众的某一指标,通知每排 (每排人数相等)座位号为14的观众留下来座谈。
探究?
类别 共同点 (1)抽 样过程中 每个个体 被抽到的 可能性相 等 (2)每 次抽出个 体后不再 将它放回 ,即不放 回抽样
