空间力系的简化与平衡
合集下载
空间力系的平衡

所示,重力G与三轮地面反力FNA、FNB、FNC构成空间平行力系。 (2) 选取坐标系Hxyz(点H为坐标原点)。 (3) 列平衡方程求解。
∑Mx(Fi)=0 FNC·CH-G·ED=0 ∑My(Fi)=0 G·EF+FNB·HB-FNA·AH=0 ∑Fz=0 FNA+FNB+FNC-G=0
解得:FNA=0.95 kN, FNB=0.05 kN, FNC=0.5kN
力对轴之矩等于零的情形:① 当力与轴相交时(d=0), ② 当力与轴平行时(Fxy=0)。即当力与轴共面时,力对轴之 矩为零。
第3章 空间力系的平衡
z
z
+
-
z -+
图 3.6
第3章 空间力系的平衡 3.2.2 合力矩定理
设有一空间力系F1、F2、…、Fn,其合力为FR,则合力对 某轴之矩等于各分力对同轴之矩的代数和,表达式为
第3章 空间力系的平衡
C
D 45° B
45 ° FB
45 °
FC O
G
A
(a)
G2
0.8 m C G
1
0.6 m 0.6 m
0.2 m
A NA
NC B
2m
NB
(b)
160 200 160
FAz Fr2 A
Ft2 r2 r1
FB2 B
FAx
Fr1 F FBx
t1
(c)
图 3.1
第3章 空间力系的平衡
5 4 68.6N 34 5
F3y F3 cos cos 100
5 3 51.5N 34 5
F3z F3 sin 100
3 51.5N 34
第3章 空间力系的平衡 (2) 计算力对轴之矩。
∑Mx(Fi)=0 FNC·CH-G·ED=0 ∑My(Fi)=0 G·EF+FNB·HB-FNA·AH=0 ∑Fz=0 FNA+FNB+FNC-G=0
解得:FNA=0.95 kN, FNB=0.05 kN, FNC=0.5kN
力对轴之矩等于零的情形:① 当力与轴相交时(d=0), ② 当力与轴平行时(Fxy=0)。即当力与轴共面时,力对轴之 矩为零。
第3章 空间力系的平衡
z
z
+
-
z -+
图 3.6
第3章 空间力系的平衡 3.2.2 合力矩定理
设有一空间力系F1、F2、…、Fn,其合力为FR,则合力对 某轴之矩等于各分力对同轴之矩的代数和,表达式为
第3章 空间力系的平衡
C
D 45° B
45 ° FB
45 °
FC O
G
A
(a)
G2
0.8 m C G
1
0.6 m 0.6 m
0.2 m
A NA
NC B
2m
NB
(b)
160 200 160
FAz Fr2 A
Ft2 r2 r1
FB2 B
FAx
Fr1 F FBx
t1
(c)
图 3.1
第3章 空间力系的平衡
5 4 68.6N 34 5
F3y F3 cos cos 100
5 3 51.5N 34 5
F3z F3 sin 100
3 51.5N 34
第3章 空间力系的平衡 (2) 计算力对轴之矩。
工程力学03力系等效简化
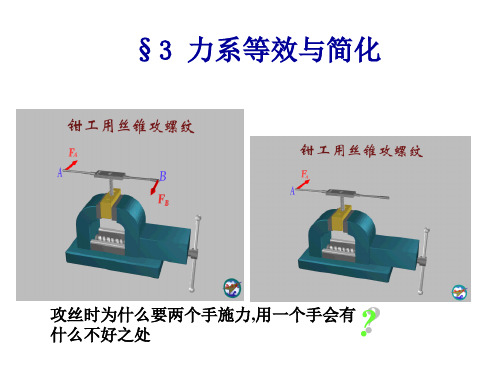
B
•
空间平行力系的中心
y
z
FR F1 F2 rC r1 r2 zC C F3 Fn r3
定义: 空间平行力系,当它有合力时, 合力的作用点C 就是该力系的中心。 平行力系的中心坐标公式
O x yC
rn
y z
xC
1)矢量形式
由合力矩定理: MO (FR ) MO (Fi )
rC FR r1 F1 r2 F2 rn Fn
i 1 i 1
•主矩 M O M i ri Fi
i 1 i 1
力系的主矢和主矩
主矢 力系中各力的矢量和称为力系的主矢。 F FR 主矢与简化中心选择无关。只有大小和 方向,没有作用点概念. 思考:力系的主矢与合力的区别? 主矩 力系中各力对简化中心之矩的矢量和 称为力系对简化中心的主矩。 M O M O ( F ) 力系对简化中心的主矩和简化中心的选择有关。 力系的主矢和主矩是决定力系对刚体作用 效应(移动和转动)的两个基本特征量。
MO (F) M MO (F1 ) MO (F2 ) 10j 10k
FR F2i F1 j 100i 100j
FR Mo 0
力螺旋
•
。
例:在边长为 a 的立方体的A、B顶点上作用有大
小均为 F 的力F1和F2,试讨论此力系的最后合成结果 a
F1
A
F2
Fn'
Mn
O
FR
F2
M2
F1'
F1
M1 F ' 2
O
MO
{F1 , F2 ,, Fn } {F1 ' , F2 ' ,, Fn ' , M1 , M 2 ,, M n } {FR , M O }
5章空间力系(交)

Fy 0
Fz F cos
由于力与轴平行 或相交时力对该轴的 矩为零,则有
M x F M x FZ Fz AB CD Fl bcos M y F M y FZ Fz BC Fl cos M z F M z Fx Fx AB CD Fl bsin
z Fz
F
x
Fx
Fxy
y Fy
二、 空间汇交力系的合成与平衡
1. 合成 将平面汇交力系合成结果推广得:
FR F1 F2 F n Fi
解析法 FR FRx i FRy j FRz k FR Fx i Fy j Fz k
合力的大小和方向为:
FR ( Fx )2 ( Fy )2 ( Fz )2
4力偶可改装性
4.4 空间力偶等效定理
空间力偶的等效条件是:两个力偶的力偶矩矢相等。
4、空间力偶系的合成 空间力偶系合成的最后结果为一个合力偶,
合力偶矩矢等于各力偶矩矢的矢量和。即:
M M1 M2 Mn Mi
根据合矢量投影定理:
Mx Mx, My My, Mz Mz
列平衡方程:(约束特点)
X 0 : X A TH cos 60 sin 45 TG cos 60 sin 45 0
Fx 0,
Fy 0,
Fz 0
M x (F ) 0, M y (F ) 0, M z (F ) 0
空间任意力系平衡的必要与充分条件为:力系中 各力在三个坐标轴上投影的代数和等于零,且各力对 三个轴的矩的代数和也等于零。
空间平行力系的平衡方程
Fz 0 Mx 0 My 0
Fz F cos
由于力与轴平行 或相交时力对该轴的 矩为零,则有
M x F M x FZ Fz AB CD Fl bcos M y F M y FZ Fz BC Fl cos M z F M z Fx Fx AB CD Fl bsin
z Fz
F
x
Fx
Fxy
y Fy
二、 空间汇交力系的合成与平衡
1. 合成 将平面汇交力系合成结果推广得:
FR F1 F2 F n Fi
解析法 FR FRx i FRy j FRz k FR Fx i Fy j Fz k
合力的大小和方向为:
FR ( Fx )2 ( Fy )2 ( Fz )2
4力偶可改装性
4.4 空间力偶等效定理
空间力偶的等效条件是:两个力偶的力偶矩矢相等。
4、空间力偶系的合成 空间力偶系合成的最后结果为一个合力偶,
合力偶矩矢等于各力偶矩矢的矢量和。即:
M M1 M2 Mn Mi
根据合矢量投影定理:
Mx Mx, My My, Mz Mz
列平衡方程:(约束特点)
X 0 : X A TH cos 60 sin 45 TG cos 60 sin 45 0
Fx 0,
Fy 0,
Fz 0
M x (F ) 0, M y (F ) 0, M z (F ) 0
空间任意力系平衡的必要与充分条件为:力系中 各力在三个坐标轴上投影的代数和等于零,且各力对 三个轴的矩的代数和也等于零。
空间平行力系的平衡方程
Fz 0 Mx 0 My 0
工程力学第五章 空间力系

cos(k, MO (F ))
Mz MO (F )
0.25
§4 - 3 空间力系向一点简化
仍设物体上只作用三个力F1 、 F2 和 F3 , 它们组成空间任意力系,在空间内任意取一 O 点,
分别将三力向此点简化。
右击
三按钮功能相同
O点称为简化中心;
R’ =F1’ + F2’ + F3’; M = M1 + M2 + M3 ; 对于力的数目为 n 的空间任意力系,推广为:
解:受力分析如图
W = 200N
∑X = 0, XA + XB-T cos30ºsin30 º= 0 ∑Y = 0, YA - T cos30 ºcos30 º= 0 ∑Z = 0, ZA + ZB - W + T sin30 º= 0
d MO MO sin
R
R
4、空间力系简化为平衡的情形
主矢R’ = 0;主矩M O = 0
§4 - 5 空间力系的平衡方程
由: R ( X )2 (Y)2 ( Z)2 0
MO [ M x (F )]2 [ M y (F )]2 [ M z (F )]2 0
合力矩定理
MO
O
O
O R’
R” d R’
d
R
R
R =∑Fi ,d= |MO| / R
∵力偶(R,R’’)的矩MO等于R 对O点的矩,即
MO = MO(R) ,而又有 MO = ∑MO(F)
∴得关系式
MO( R ) = ∑MO(F )
即:空间任意力系的合力对于任意一点的矩等于
各分力对同一点的矩的矢量和。
阴影部分的面积。
工程力学:第2章 力系的简化

F1sin45 F2sin45 0 FAsin30 F1cos45 cos30 F2 cos45 cos30 0 FAcos30 F1cos45 sin30 F2cos45 sin30 P 0
B FB1
相同的均质杆围成正方形,求绳EF的拉力。
要求:
用最少的方 程求出绳EF受 的力
FAy
FAx
A
E
P
FDy
FDx
D
G
P
B
F
P
C
FDy FDx
D
G
P
FDy FDx
D
FCy FCx
C
FBx FT
G
P
FBy
B
F
P
C
例3-3
q
FAx A
M B
2a
P
FAy
4a
FB
ll
30
F
M
3l P
q
例3-4
F
体等效于只有一个力偶的作用,因为力偶可以在刚体平
面内任意移动,故这时,主矩与简化中心O无关。
③ FR≠0,MO =0,即简化为一个作用于简化中心的合力。这时,
简化结果就是合力(这个力系的合力), FR FR 。(此时
与简化中心有关,换个简化中心,主矩不为零)
④ FR 0, MO 0 ,为最一般的情况。此种情况还可以继续 简化为一个合力 FR 。
FAy
B FB1x
C
M
B
D
Cr
•
E
A
300 F E
FA
FT
C
F A1
FA
求:销钉A所受的力
M
B D
FD D C
工程力学第4章 力系的平衡

2
即空间一般力系平衡的解析条件是力系中所有各力 在任一轴上投影的代数和为零,同时力系中各力对任一 轴力矩的代数和为零。式(4.2)称为空间一般力系的平 衡方程(equationsofequilibrium ofthreedimensionalforcesystem inspace)。 应当指出,由空间一般力系平衡的解析条件可知, 在实际应用平衡方程时,所选各投影轴不必一定正交, 且所选各力矩轴也不必一定与投影轴重合。此外,还可 用力矩方程取代投影方程,但独立平衡方程总数仍然是 6个。
30
4.3.1 有主次之分物体系统的平衡 有主次之分的物体系统,其荷载传递规律是:作用 在主要部分上的荷载,不传递给相应的次要部分,也不 传递给与它无关的其他主要部分;而作用在次要部分上 的荷载,一定要传递给与它相关的主要部分。
31
32
据此,先分析次要部分BD,其受力图如图4.11(b) 所示。建立图示参考系Oxy,列平衡方程并求解。由于 本题只要求出D处的约束反力,而不必要求出B处的约 束反力,故
12
13
建立参考系 Bxy,列平衡方程,求未知力。
14
15
例4.ቤተ መጻሕፍቲ ባይዱ 图4.5所示为一管道支架,其上搁有管道,设 每一支架所承受的管重G1=12kN,G2=7kN,且架重不计。 求支座A和C处的约束反力,尺寸如图所示。
16
17
解 取刚架AB为研究对象,其上所受力有:已知的 集中力F、集度为q的均布荷载,集中力偶;未知的3个 约束反力FAx,FAy,MA。刚架AB的受力图如图4.6(b) 所示。各力组成一平面一般力系。建立图示Oxy坐标系, 列平衡方程求解
9
2.平面一般力系平衡方程的其他形式 (1)二矩式平衡方程
空间力系的平衡方程式及其应用

即与各坐标轴相交。因此各力对坐标轴的矩均为零,即式(3-17)中,
M x (F ) 0 , M y (F ) 0, M z (F ) 0 。于是,空间汇交力系的平衡方程
只有三个,即
Fx 0
Fy
0
Fz
0
(3-18)
(2)空间平行力系
若取z轴平行于力系中各力的作用线,则 Oxy 坐标面与各力作用线
衡的必要与充分条件是:力系的主矢和力系对于任意点的主矩矢
都等于零。即
FR 0
MO 0
根据式(3-14)和式(3-16),上述条件可写成
空间任意力系平衡的必要与充分条 件是:力系中各力在任一直角坐标 系中每一轴上的投影的代数和等于 零,以及各力对每一轴的矩的代数 和也等于零。
Fx 0
Fy 0
式中,负号表明 FB ,FC 的实际方向与假设相反,即两杆均受压力。
例3-4
O1 和 O2 圆盘与水平轴 AB 固连,O1 盘垂直于z轴,O2 盘垂直于x轴,
力的矢量和。
即
FR F1 F2 Fn Fi (3-11)
图3-9
附加力偶系可合成为一个空间力偶,其力偶矩 MO,等于各附加力
偶矩的矢量和,亦即等于原力系中各力对于简化中心O的矩的矢量和。
MO MO (F1) MO (F2 ) MO (Fn ) MO (Fi )
F称R 为原力系的主矢,称为原力系对简化中心O的主矩矢 M。O
Fz 0
M
x
(F
)
0
M y (F ) 0
M
z
(F
)
0
(3-17)
空间任意力系是物体受力的最一般情况,其他类型的力系都可 以认为是空间任意力系的特殊情形,因而它们的平衡方程也可 由方程式(3-17)导出,具体如下。
空间力系平衡方程及应用

空间任意力系的平衡方程组由六个方程组 成,对于受空间任意力系作用而处于平衡的物 体,运用方程组最多求出六个未知量。
根据空间任意力系的平衡方程,可以推出 空间汇交力系和空间平行力系的平衡方程。
空间 力系 的平 衡方 程及 应用
1.空间汇交力系的平衡方程
由于空间汇交力系的简化结果只有一个合力R,因 此,力系平衡的平衡条件是力系的合力R为-9所示的悬臂刚架中,若已知荷载F1=20 kN,F2=100 kN,q=10 kN/m,尺寸H=3 m,h=1.5 m,l=3 m。不考虑刚架的自重,求刚架所受的约
束反力。
空间 力系 的平 衡方 程及 应用
空间 力系 的平 衡方 程及 应用
【解】 (1)以刚架为研究对象画受力图。 因A端为固定端,阻碍被约束构件向任意方向 移动和绕任意轴转动,故其约束反力为三个相互垂 直的分力和三个作用面相互垂直的分力偶,如图39所示,刚架所受力系为空间任意力系。 (2)建立坐标系,如图3-9所示,列平衡方 程。
(3-9)
空间汇交力系的平衡方程组由三个方程组成,利 用方程组最多只能求出三个未知量。
空间 力系 的平 衡方 程及 应用
2.空间平行力系的平衡方程
当空间平行力系中的各力的作用线与三维 直角坐标系的z轴平行时,无论力系是否平衡, 力系中各力在x,y轴上的投影都是零,且各力 对z轴的力矩也是零,因此,空间平行力系的 平衡方程组为
空间力 系的平衡方
程及应用
1.1 空间任意力系的平衡方程 1.2 空间力系平衡方程的应用
由空间任意力系的平衡条件,可以得到空间任 意力系的平衡的解析表达式为
(3-8)
式(3-8)说明空间任意力系平衡时,力系中 的各力在直角坐标系中的各轴上的投影代数和为零, 对各轴之矩的代数和也为零。
