空间任意力系的简化
合集下载
任意力系的简化(基本知识点)
3、刚体的重心 刚体所受到的重力系可看作是一个同向的平行力系，它们必存在合力， 刚体重力系的中心称为刚体的重心。刚体的重心在刚体内或其延拓部分占有 确定位置，该位置与刚体在空间的放置情况无关。当刚体的质量分布不均匀 时，其重心和几何中心（形心）不重合。只有均质刚体的重心才与其形心重 合。通常用分割法或负面积法（或负体积法）求组合体的重心。 4、线分布载荷的简化 线分布载荷是指沿构件轴线连续作用的载荷，其大小和方向用载荷集度 表示。线分布载荷的载荷集度是指作用于构件单位长度（该术语在极限意义 下使用）上的力的大小和方向，其单位为N/m。几种常见的线分布载荷的合 力大小及其作用线位置如下：
第三章
ห้องสมุดไป่ตู้
任意力系的简化
基本知识点
1．力系的简化的定义 用一简单力系等效地代替一复杂力系称为力系的简化或合成。 2．力的平移定理 若将作用于刚体上的力 F平移至同一刚体上不在力 F的作用线 上的其它点 o，则必须相应增加一个附加力偶，其力偶矩M等于 原力 F 对平移点 o 的矩，才能保证原力对刚体的作用效果。这一 结论称为力的平移定理。显然M垂直于由点o与原力F的作用线所 作出的平面。 上述定理的逆定理也成立，即当作用于刚体上某点 o的某个 力F1与作用于同一刚体上的某个力偶的力偶矩垂直时，则该力和 力偶可以合成为一个力F，其力矢与原长F1相同，平移的垂直方 向为F1×M方向，平移和垂直距离为M/F1。 力的平移定理表明，一个力可以等效于一个力和一个力偶。 而其逆定理则表明，可以将同一平面内的一个力和一个力偶等效 于一个力。力的平移定理是任意力系向某点简化的理论基础。
第三章 第四节 空间力系的简化
O O O O'
' FR
'' ' FR d FR FR
O'
d FR
MO(FR) =MO=SMO(F ) Mx(FR)=SMx(F )
空间力系对点(轴)之矩的合力矩定理
4. 空间力系简化为力螺旋的情形 FR' ≠0 MO ≠ 0且FR' // MO 力螺旋 ' FR MO ' FR ' FR MO O O O 右螺旋 力系的中心轴：力螺旋中力的作用线 左螺旋
F1' M2 M1
F2'
O
FR' MO
Fn' ห้องสมุดไป่ตู้M F3' Mn 3 Mi=MO(Fi )
2. 主矢和主矩 主矢：空间力系中所有各力的矢量和 (与简化中心的位置无关)
FR'= SF
主矩：各力对于任选的简化中心 O之矩的矢量和 MO=SMO(F ) (一般与简化中心的位置有关)
三、空间力系的简化结果 合力矩定理 1. 空间力系平衡的情形 FR' =0 MO=0 2. 空间力系简化为一合力偶的情形 FR' =0 MO≠0 (主矩与简化中心的位置无关) 3. 空间力系简化为一合力的情形 合力矩定理 (1) FR' ≠0 MO=0 合力的作用线通过简化中心O，合力矢等于原力系的主矢。 (2) FR' ≠0 MO ≠ 0且FR' ⊥ MO 合力的作用线通过另一点O ' ，d=MO /FR MO
一、空间力的平移定理 空间力的平移定理：作用在刚体上的一个力，可平行移至刚体 中任意一指定点，但必须同时附加一力偶，其力偶矩矢等于原 力对于指定点的力矩矢。
第四节 空间力系的简化
' FR
'' ' FR d FR FR
O'
d FR
MO(FR) =MO=SMO(F ) Mx(FR)=SMx(F )
空间力系对点(轴)之矩的合力矩定理
4. 空间力系简化为力螺旋的情形 FR' ≠0 MO ≠ 0且FR' // MO 力螺旋 ' FR MO ' FR ' FR MO O O O 右螺旋 力系的中心轴：力螺旋中力的作用线 左螺旋
F1' M2 M1
F2'
O
FR' MO
Fn' ห้องสมุดไป่ตู้M F3' Mn 3 Mi=MO(Fi )
2. 主矢和主矩 主矢：空间力系中所有各力的矢量和 (与简化中心的位置无关)
FR'= SF
主矩：各力对于任选的简化中心 O之矩的矢量和 MO=SMO(F ) (一般与简化中心的位置有关)
三、空间力系的简化结果 合力矩定理 1. 空间力系平衡的情形 FR' =0 MO=0 2. 空间力系简化为一合力偶的情形 FR' =0 MO≠0 (主矩与简化中心的位置无关) 3. 空间力系简化为一合力的情形 合力矩定理 (1) FR' ≠0 MO=0 合力的作用线通过简化中心O，合力矢等于原力系的主矢。 (2) FR' ≠0 MO ≠ 0且FR' ⊥ MO 合力的作用线通过另一点O ' ，d=MO /FR MO
一、空间力的平移定理 空间力的平移定理：作用在刚体上的一个力，可平行移至刚体 中任意一指定点，但必须同时附加一力偶，其力偶矩矢等于原 力对于指定点的力矩矢。
第四节 空间力系的简化
空间任意力系
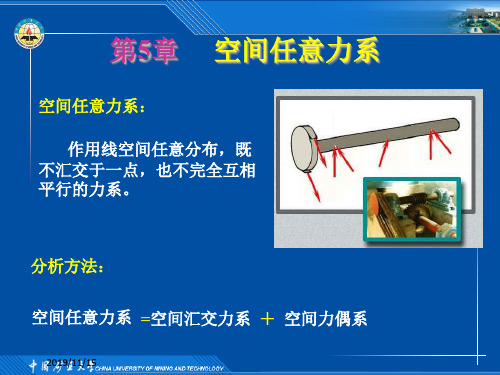
FC
最大载重Pmax是多少。
Q FB
P
D
解: 取起重机为研究对象
A
B,C
My(F)0, FAaco3s0Qa3co3s0Pclos0
MC'x(F)0,
a FA2
FBaQa2P(a2lsin)0
y C
x’
Fz 0, FAFBFCPQ0
A
ED
x
解得: FA=19.3kN， FB=57.3kN， FC=43.4kN
d O1
O
MO MO cos MO MO sin
d MO MO sin
FR
FR
一般情形下空间任意力系可合成为力螺旋
(4) 空间任意力系平衡的情形
● F′R=0，MO=0
2019/11/15
原力系平衡
内容回顾
空间力系的简化与合成
主矢
主矩
最后结果
说
明
FR′ = 0
MO = 0 MO≠0
§5-5 空间任意力系的平衡条件及其应用
1、平衡条件及平衡方程：
平衡条件：
由平衡力系定理可知，空间一般力系平衡的充要条件：力 系的主矢和对任一点的主矩都等于零，即：
平衡方程：
FR Fi 0
M O M O i 0
由主矢与主矩的计算式，有
F R (F x F x i )0 2 i, (F F yy ) i2 i0 ,(F F zz i )i2 0
② 空间任意力系的平衡条件及其应用；
2019/11/15
§5-4 空间任意力系的简化
1. 空间力线平移定理
作用于刚体的力 F 可等效地平移到刚体上的任一点O， 但须附加一力偶，此附加力偶矩 矢M 等于原力对平移点O 的力矩矢MO（F）。
空间任意力系的简化结果分析
FT
6 P 100 6
6N (拉力)
Mil1 0
FAx 4 FT1
4 20 20
FAx
30பைடு நூலகம்6
FT
2 100N 20
Mil2 0
FAx 4 FAy 2 0
FAy 2FAx 200 N
z
E FAz
2m
FAx
A
0时，空间力系为平衡力系
7
§3–2 空间力系的平衡
平衡力系所要满足的条件称为力系的平衡条件。
1.空间力系的平衡条件
任意空间力系平衡的充要条件是：力系的主矢 定点O的主矩 M O 全为零。
FR
和对任一确
即
n
FR Fi 0
i 1
n
（7.1）
M O M O (Fi ) 0
sin BC
42 32
0.8944
AB
42 32 2.52
cos 0.4472
sin CD
4
0.8
BC
42 32
cos BD
3
0.6
BC
42 32
z 4m
600
F2
F1
F3
x
Fx F sin cos 1500 0.8944 0.6 805N
3
主矢和主矩的计算
主矢—通过投影法
先计算得到主矢在 各轴上的投影
根据它们，可得到 主矢的大小和方向
n
FRx
Fxi
i 1
n
FRy
第二章力系的简化
一、力的平移定理
M= MB(FA)=FA·a
FA
A B
FA
A
FB
a
B
FB´
M
A
FB
B
作用在刚体上的力，可以等效平移到刚体上任一指 定点，但必须在该力和指定点所确定的平面内附加一 力偶，附加力偶的力偶矩等于原力对指定点的矩。
注意：只有在研究力的运动效应时，力才能平行移动。
研究变形效应时一般是不能移动的。
FR MO O
FR FR
d
O
A
FR
d
O
A
主矢与主矩垂直，FR
FR M
可简化为一个合力
HOHAI UNIVERSITY ENGINEERING MECHANICS
(a) FR ⊥MO
表明FR与MO在同一平面，即共面
共面的力与力偶合成一个力。 FR
合力为F‘R,等于原力的合力FR
O
MO
作用线过新的简化中心
练习1：确定图示力系的合力大小及作用线位置。
z
4kN
6kN
2m
12kN 3m
y
Ox
x y FR Fy 0
Miy 0
Mix 0
解：
该力系为空间平行力 系，各力指向一致，可知 该力系简化为一个铅垂向 下的力。
FR 22kN
x 12 3 1.636m 22
y 6 2 0.545m 22
空间汇交力系
平面汇交力系
二、力偶系
平面力系
空间力系
HOHAI UNIVERSITY ENGINEERING MECHANICS
HOHAI UNIVERSITY ENGINEERING MECHANICS
空间力系的平衡方程式及其应用
即与各坐标轴相交。因此各力对坐标轴的矩均为零，即式（3-17）中，
M x (F ) 0 ， M y (F ) 0， M z (F ) 0 。于是，空间汇交力系的平衡方程
只有三个，即
Fx 0
Fy
0
Fz
0
（3-18）
（2）空间平行力系
若取z轴平行于力系中各力的作用线，则 Oxy 坐标面与各力作用线
衡的必要与充分条件是：力系的主矢和力系对于任意点的主矩矢
都等于零。即
FR 0
MO 0
根据式（3-14）和式（3-16），上述条件可写成
空间任意力系平衡的必要与充分条 件是：力系中各力在任一直角坐标 系中每一轴上的投影的代数和等于 零，以及各力对每一轴的矩的代数 和也等于零。
Fx 0
Fy 0
式中，负号表明 FB ，FC 的实际方向与假设相反，即两杆均受压力。
例3-4
O1 和 O2 圆盘与水平轴 AB 固连，O1 盘垂直于z轴，O2 盘垂直于x轴，
力的矢量和。
即
FR F1 F2 Fn Fi （3-11）
图3-9
附加力偶系可合成为一个空间力偶，其力偶矩 MO，等于各附加力
偶矩的矢量和，亦即等于原力系中各力对于简化中心O的矩的矢量和。
MO MO (F1) MO (F2 ) MO (Fn ) MO (Fi )
F称R 为原力系的主矢，称为原力系对简化中心O的主矩矢 M。O
Fz 0
M
x
(F
)
0
M y (F ) 0
M
z
(F
)
0
（3-17）
空间任意力系是物体受力的最一般情况，其他类型的力系都可 以认为是空间任意力系的特殊情形，因而它们的平衡方程也可 由方程式（3-17）导出，具体如下。
静力学-空间任意力系的简化
{F1, F2,, Fn , P1, P2,, Pm}
F’ F”
AF
B
2
定理：作用在刚体上的力，沿其作用线移动后， 不改变其作用效应。
刚体
F
F
FF
变形体
F
F
FF
作用于刚体上力的三要素:大小、方向、作用线 3
2、力的平移
F
F A
B
A
B
F
F A
B
F’
F MB
A rBA
B
力的平 移定理
{F}A {F', MB}B , F' F, MB rBA F 4
合力偶
问题: 向不同点简化是否得到不同的合力偶?
6
Mi ri Fi
Fi
M
' i
ri'
Fi
ri' o 'o ri
ri
oห้องสมุดไป่ตู้
M
' i
ri'
Fi
ri'
o'o ri Fi
o’
M
' i
o 'o ri Fi o 'o Fi ri Fi Mi
结论: 如果 FR ,则0向不同点简化得到相同的合力偶. 7
§2-3、空间任意力系的简化 •空间任意力系：力作用线在空间任意分布的力系
z
F1
o
F2
F3
y
x Fi Fn
问题： 空间任意力系如何简化？
1
一、力的移动 1、力沿作用线移动
加减平衡力系原理： 在刚体上增加或减去
一组平衡力系，不会改变 原力系对刚体的作用效应
F’ F”
AF
F’ F”
AF
B
2
定理：作用在刚体上的力，沿其作用线移动后， 不改变其作用效应。
刚体
F
F
FF
变形体
F
F
FF
作用于刚体上力的三要素:大小、方向、作用线 3
2、力的平移
F
F A
B
A
B
F
F A
B
F’
F MB
A rBA
B
力的平 移定理
{F}A {F', MB}B , F' F, MB rBA F 4
合力偶
问题: 向不同点简化是否得到不同的合力偶?
6
Mi ri Fi
Fi
M
' i
ri'
Fi
ri' o 'o ri
ri
oห้องสมุดไป่ตู้
M
' i
ri'
Fi
ri'
o'o ri Fi
o’
M
' i
o 'o ri Fi o 'o Fi ri Fi Mi
结论: 如果 FR ,则0向不同点简化得到相同的合力偶. 7
§2-3、空间任意力系的简化 •空间任意力系：力作用线在空间任意分布的力系
z
F1
o
F2
F3
y
x Fi Fn
问题： 空间任意力系如何简化？
1
一、力的移动 1、力沿作用线移动
加减平衡力系原理： 在刚体上增加或减去
一组平衡力系，不会改变 原力系对刚体的作用效应
F’ F”
AF
4任意力系的简化
这个力偶是力系的主矩，等于各力对该点之矩的矢量和。 主矢的大小、方向与简化中心无关。 主矩的大小、方向与简化中心有关。
Theoretical Mechanics
返回首页
任意力系的简化
3 力系的简化结果分析
1.力系简化为合力偶M
F'R = 0，MO≠0 力偶矩M = MO = ∑MO(Fi) 其大小、方向与简化中心无关
由此可知：对于沿直线分布的垂直分布载荷来说，其合力
的大小等于分布载荷图形的面积，合力作用线则通过该图形的
形心。
Theoretical Mechanics
返回首页
平行力系与重心
1 平行力系的简化 ·平行力系的中 心
例 ：求图示分布载荷的合力及对A点之矩。
解：将分布载荷图形分成两个三 角形，每个三角形载荷合力大小 分别为 1 1
2 力系向一点简化· 主矢和主矩
n
n
MO
称为该力系的主矢 MO称为该力系对简化中心O的主矩。
FR
Theoretical Mechanics
返回首页
任意力系的简化
2 力系向一点简化· 主矢和主矩
结
论
任意力系向一点简化的结果为作用于该点的一个力和一
个力偶。这个力是力系的主矢，等于力系中各力的矢量和，
任意力系的简化
1 力的平移定理
力的平移定理
FR FR FR
FR
M
, FR ) (FR )O ( FR
Theoretical Mechanics
FR
+ M
返回首页
任意力系的简化
结 论
力的平移定理：作用于刚体上的力F ，可以平移 至同一刚体的任一点O ，但必须增加一个附加力偶， 附加力偶的力偶矩等于原力F对于平移点O之矩，即
Theoretical Mechanics
返回首页
任意力系的简化
3 力系的简化结果分析
1.力系简化为合力偶M
F'R = 0，MO≠0 力偶矩M = MO = ∑MO(Fi) 其大小、方向与简化中心无关
由此可知：对于沿直线分布的垂直分布载荷来说，其合力
的大小等于分布载荷图形的面积，合力作用线则通过该图形的
形心。
Theoretical Mechanics
返回首页
平行力系与重心
1 平行力系的简化 ·平行力系的中 心
例 ：求图示分布载荷的合力及对A点之矩。
解：将分布载荷图形分成两个三 角形，每个三角形载荷合力大小 分别为 1 1
2 力系向一点简化· 主矢和主矩
n
n
MO
称为该力系的主矢 MO称为该力系对简化中心O的主矩。
FR
Theoretical Mechanics
返回首页
任意力系的简化
2 力系向一点简化· 主矢和主矩
结
论
任意力系向一点简化的结果为作用于该点的一个力和一
个力偶。这个力是力系的主矢，等于力系中各力的矢量和，
任意力系的简化
1 力的平移定理
力的平移定理
FR FR FR
FR
M
, FR ) (FR )O ( FR
Theoretical Mechanics
FR
+ M
返回首页
任意力系的简化
结 论
力的平移定理：作用于刚体上的力F ，可以平移 至同一刚体的任一点O ，但必须增加一个附加力偶， 附加力偶的力偶矩等于原力F对于平移点O之矩，即
3.2、空间力系的简化(2-1)(美化)
空间力系的简化RR F F F F F F F F =++=++=321'3'2'1')()()(321F M F M F M M o o o o ++=力系主矢: R F 力系主矩: oM 空间任意力系=主矢+主矩力系简化结果讨论:0=∑=i R F F )(])[()(i Ai i BA i Ai BA i Bi B F r F r F r r F r M ⨯+⨯∑=⨯+∑=⨯∑=AA i BA M M F r +=+∑⨯=01）F R =0、M O =0。
原力系是平衡力系。
2）F R =0、M O ≠0。
原力系等效于一个力偶。
力偶矩是自由矢量，可以平移到空间任意位置而不改变作用效果，所以主矢为零时主矩是一个与简化点位置无关的常量3）F R ≠0、M O =0。
原力系等效于一个力，该力经过简化点，称为原力系的合力。
)(≠∑=i A A F M M力系简化结果讨论:4.1）o R M F ⊥ROA OA O O F r F r F M M ⨯=⨯==)(4）F R ≠0、M O ≠0。
这是最一般的情况，又可细分为以下三种类型：4.2）F R ∥M O 。
主矢力F R 垂直于主矩力偶M O 中两力（F 1、F 1′）所在的平面，这时主矢力与主矩力偶怎么才能化简为一个力？力系简化结果讨论:空间力系的简化4.2）F R ∥M O 。
但力偶矩是自由矢量，可以把主矩M O 平移到主矢力F R 作用线上（图示），从而得到一个力螺旋：力螺旋由一个力和一个力偶构成，且力矢量与力偶矩矢量重合（即：力垂直于力偶中两力所在的平面）。
力螺旋对物体的作用效果是力与力偶作用效果的叠加（平移加旋转），如钻孔时钻头对工件的作用力就是力螺旋，拧螺钉时螺丝刀对螺钉的作用力也是力螺旋。
力螺旋不能再继续简化，它可以表示成图c 、d 所示任一形式。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）力系简化结果讨论://O O O M M M -=⊥2//)()()cos (RR R O R R R R O R R O O F F F M F F F F M F F M M ⋅⋅=⋅⋅=⋅=α4.3）F R 既不平行也不垂直于M O 。
第三章力系的简化
M O M O ( Fi )
力系若有合力，力系合力对任意轴的 矩等于力系各力对同一轴的矩的矢量和；
M x M x ( Fi )
7. 空间任意力系简化为力螺旋
简化后，若FR0，MO0，且FR与MO平行， 此时无法进一步简化。 这样力与力偶作用面垂直的情况称为力螺旋。
FR与MO同向，称右手螺旋；
4.平面任意力系的简化
1) 平面任意力系向一点简化 平面任意力系
力线平移
平面汇交力系+平面力偶系
平面汇交力系+平面力偶系
合成
平面汇交力系合力FR
平面力偶系合力偶MO
简化点O任选，称简化中心 简化后平面汇交力系的合力FR，有：
简化后平面力偶系的合力偶MO，有：
平面任意力系向作用面内一点简化后得到一个 力和一个力偶，该力的主矢等于原力系的主矢，该 力偶的力偶矩等于原力系对简化中心的主矩。 简化后有以下几种情况： 1） 若FR=0，MO0，则力系合成为一个合力偶， 合力偶矩等于原力系对简化中心的主矩。这种情 况下，主矩与简化中心的位置无关； 2） 若FR0，MO=0，则力系合成为一个合力， 主矢FR与原力系主矢FR相等。主矢FR通过简化 中心。合力与简化中心的位置有关，换一个简化 中心，则MO不为零。
3）结论
任意平面汇交力系：
可以简化为一合力，合力的大 小与方向等于各分力的矢量和（几 何和），合力的作用线通过汇交点。 用矢量表示：
平面汇交力系平衡的充要条件是：该力系的 合力等于零。
几何法求解平面汇交力系，一般适合三个 力汇交的情况
例：如图，为汽车制动机 构的一部分。驾驶员蹬踩 力F=212N，方向与水平 面夹角α=45º。平衡时， DA垂直，BC水平，求拉 杆BC所受的力。已知， EA=24cm，DE=6cm，点 在上，机构不计自重，C、 B、D均为光滑铰链。
理论力学第三章 任意力系的简化与平衡条件
例3-2 已知：涡轮发动机叶片轴向力F=2kN，力偶矩
M=1kN.M, 斜齿的压力角=20 ,螺旋角 。 =10 ,齿轮节圆半径 r=10cm。不计发动 机自重。 O1O2=L1=50cm, O2A=L2=10cm. 求： FN, O1,O2处的约束力。
。
第三章 力系的简化与平衡条件
§3-5 力系的平衡条件
3
F2 F3
1
F'
F1
1 O 200 1
x
2
1 3 1 FRy F1 F2 F3 = -161.6(N) 2 10 5
第三章 任意力系的简化与平衡条件
§3-4 力系简化计算
解：(1)先将力系向O点简化，求主矢和主矩。 FRx FRy =466.5(N) 2 2 FR
Xi 0 F x F2x Fr 0 1
F y F2y F 0 1
Zi 0
F z Fa F 0 1
第三章 力系的简化与平衡条件
§3-5 力系的平衡条件
例3-2 解： 3、列平衡方程
Mx (F) 0
F2 y L1 F (L1 L2 ) 0
y
100 1
F
80
3
Байду номын сангаас
F2 F3
1
F'
F1
1 O 200 1
x
2
第三章 任意力系的简化与平衡条件
§3-4 力系简化计算
例3-1 (1)先将力系向O点简 解： 化，求主矢和主矩。 1 1 F2 FRx F1 10 2 2 F3 5 = -437 .6（N）
y
100 1
F
力系的简化
j
k
MC(F) a·Sinθ a·CosθCosα a·Sinα =- a·CosθCosαi+FaSin θj
=
0
0
0
令CB=b 则CB =bSinαj + bSinαk
e CB CB
b sin j
sin j cos k
b2 sin 2 b2 cos2
故MC(F)在AB轴上得投影
MAB(F)=MC(F )eCB=FaSinαSinθ
三. 力系向一点的简化
（一）. 空间汇交力系的简化（将其简化为一合力）
力的作用线在空间任意分布的力系成为空间任 意力系。各力作用线汇于一点的空间力系，成为空 间汇交力系。
空间汇交力系的合理等于各分力的矢量和（满足 平行四边形法则），合力作用线通过汇交点，即
FR=F1+F2+…… 又由于+FFni=xii+yij+zik
合力偶对各坐标轴得方向余弦：
cos(M,i)= Mx 0.6786 M cos(M,i)= M z 0.2811 M cos(M,i)= M z 0.6786 M
(三). 空间任意力系得简化
FacSinSin
a2 b2
例2.2 作用于手柄上的力F=100N,求①力F 对x轴的
矩 ②力F 对原点o的矩.
解:画出r , r =0.1i+0.4k
又有
z y
o
F = 100(Sin60°cos45°i+Sin60°sin45°j
-cos60°k)
x
100
2i 4
2 4
j
3k 4
0.4m
第二章 力系的简化
右手定则：
空间任意力系
称为空间力偶系的主矩 由力对点的矩与力对轴的矩的关系，有
Mo Mx (F)i M y (F) j Mz (F)k
式中，各分别表示各 Mx (F), M y (F), Mz (F)力
对 x，y，z ,轴的矩。
12
FRx —有效推进力
FRy —有效升力 FRz —侧向力
MOx —滚转力矩
力偶矩 M rBA F
Mo (F, F) Mo (F) Mo (F) rA F rB F
因 F F
Mo (F, F) (rA rB ) F M
5
（3）只要保持力偶矩不变，力偶可在其作用面内任意移转， 且可以同时改变力偶中力的大小与力偶臂的长短，对刚体的 作用效果不变.
1
方向余弦
cos(FR , i )
Fx FR
cos(FR ,
j)
Fy FR
cos(FR ,k Nhomakorabea)
Fz FR
空间汇交力系的合力等于各分力的矢量和，合力的作用线通过汇交点.
知识要点回顾
空间汇交力系的平衡条件
空间汇交力系平衡的充分必要条件是：
Fx 0 Fy 0
称为空间汇交力系的平衡方程.
=
=
=
M
(
F1 ,
F1)
rBA
F1
M (FR , FR) rBA FR rBA (F1 F2 )
rBA F1 rBA F2 rBA F1 M (F1, F1)
6
(4)只要保持力偶矩不变，力偶可从其所在平面移至另 一与此平面平行的任一平面，对刚体的作用效果不变.
Mo Mx (F)i M y (F) j Mz (F)k
式中，各分别表示各 Mx (F), M y (F), Mz (F)力
对 x，y，z ,轴的矩。
12
FRx —有效推进力
FRy —有效升力 FRz —侧向力
MOx —滚转力矩
力偶矩 M rBA F
Mo (F, F) Mo (F) Mo (F) rA F rB F
因 F F
Mo (F, F) (rA rB ) F M
5
（3）只要保持力偶矩不变，力偶可在其作用面内任意移转， 且可以同时改变力偶中力的大小与力偶臂的长短，对刚体的 作用效果不变.
1
方向余弦
cos(FR , i )
Fx FR
cos(FR ,
j)
Fy FR
cos(FR ,k Nhomakorabea)
Fz FR
空间汇交力系的合力等于各分力的矢量和，合力的作用线通过汇交点.
知识要点回顾
空间汇交力系的平衡条件
空间汇交力系平衡的充分必要条件是：
Fx 0 Fy 0
称为空间汇交力系的平衡方程.
=
=
=
M
(
F1 ,
F1)
rBA
F1
M (FR , FR) rBA FR rBA (F1 F2 )
rBA F1 rBA F2 rBA F1 M (F1, F1)
6
(4)只要保持力偶矩不变，力偶可从其所在平面移至另 一与此平面平行的任一平面，对刚体的作用效果不变.
理论力学：空间任意力系的简化
理论力学
• 空间任意力系的简化与平衡条件
2020/12/9
1
理论力学 BUAA
空间任意力系的简化
三、空间任意力系简化结果的讨论
空间任意力系 {F1, F2,, Fn} {FR , MO} 简化结果
1、 FR 0, MO 0 2、 FR 0, MO 0
平衡力系 合力 (过简化点O)
3、 FR 0, MO 0
2020/12/9
10
理论力学
§2-4 各类力系平衡条件
例：结构如图所示，不计构件自重。已知主动力F（作用于杆 的中点），确定铰链O、B约束力的方向并比较其大小。
FA A
F O
1、研究OA杆 B
2、研究AB杆
A
FA
F
B
O
FB
FO FA
（A）
FB
F
FO FB FA FO
FO
（B）
FB
FB FA FO
F
2020/12/9
11
理论力学
§2-4 各类力系平衡条件
二、空间任意力系的平衡条件
空间任意力系简化 {F1, F2 ,, Fn} {FR , MO}
平衡
FR 0, MO 0
n
n
FR Fi ' Fi
i 1
i 1
n
n
MO Mi ri Fi
i1
i1
FR ( Fx )2 ( Fy )2 ( Fz )2 MO ( MOx )2 ( MOy )2 ( MOz )2
二力平衡原理
作用于刚体上的二力为平衡力系的充分必要条件是此 二力等值、反向、共线。
三力平衡定理
作用于刚体上的三个力若为平衡力系，则这三个力的 作用线共面，或汇交于一点或彼此相互平行。
• 空间任意力系的简化与平衡条件
2020/12/9
1
理论力学 BUAA
空间任意力系的简化
三、空间任意力系简化结果的讨论
空间任意力系 {F1, F2,, Fn} {FR , MO} 简化结果
1、 FR 0, MO 0 2、 FR 0, MO 0
平衡力系 合力 (过简化点O)
3、 FR 0, MO 0
2020/12/9
10
理论力学
§2-4 各类力系平衡条件
例：结构如图所示，不计构件自重。已知主动力F（作用于杆 的中点），确定铰链O、B约束力的方向并比较其大小。
FA A
F O
1、研究OA杆 B
2、研究AB杆
A
FA
F
B
O
FB
FO FA
（A）
FB
F
FO FB FA FO
FO
（B）
FB
FB FA FO
F
2020/12/9
11
理论力学
§2-4 各类力系平衡条件
二、空间任意力系的平衡条件
空间任意力系简化 {F1, F2 ,, Fn} {FR , MO}
平衡
FR 0, MO 0
n
n
FR Fi ' Fi
i 1
i 1
n
n
MO Mi ri Fi
i1
i1
FR ( Fx )2 ( Fy )2 ( Fz )2 MO ( MOx )2 ( MOy )2 ( MOz )2
二力平衡原理
作用于刚体上的二力为平衡力系的充分必要条件是此 二力等值、反向、共线。
三力平衡定理
作用于刚体上的三个力若为平衡力系，则这三个力的 作用线共面，或汇交于一点或彼此相互平行。
第二章力系简化
例 在图示长方体的顶点B处作 用一力F，F=700N。分别求力F 对各坐标轴之矩，并写出力F对 点O之矩矢量Mo(F)。 解1：力F矢量作用点坐标为： B( x, y, z ) B(2,3,0) 力F矢量在三个坐标轴的投影为：
( Fx , Fy , Fz ) ( 100 14,150 14,50 14)
F2
z
M1 M3
45°
F2 F3 O F1
y
M2
F3 F1
O
45°
y
x
x
M x M 1x M 2 x M 3 x 0
M y M 1 y M 2 y M 3 y 11.2 N m
M z M 1z M 2 z M 3 z 41.2 N m
3. 平面力偶系的合成与平衡
作为空间力偶系的特例，平面力偶系合成的结果 是位于各分力偶作用平面内的一个合力偶， 该合力偶矩等于各分力偶矩的代数和。即
M M1 M 2 M n M i
代数和
平面力偶系平衡的必要和充分条件是：各分力偶 的代数和等于零。即
M Mi 0
[ M O ( F )]x M x ( F ) [ M O ( F )] y M y ( F ) [ M O ( F )]z M z ( F )
力矩关系定理： 力对点之矩矢量 在过该点之轴上 的投影等于该力 对该轴之矩.
M O ( F ) M x ( F )i M y ( F ) j M z ( F )k
M D
30 30
B R C
A
E
解: 1.研究AB杆
M i 0
M FD AD 3R FD
M D
工程力学_05空间力系
0, MO 0 时，空间力系为平衡力系。 当 FR
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系向任一点简化可得到一个力和一个力偶。 这个力通过简化中心，称为力系的主矢，它等于各 个力的矢量和，并与简化中心的选择无关。 这个力偶的力偶矩矢称为力系对简化中心的主矩， 并等于力系中各力对简化中心之矩矢的矢量和，并 与简化中心的选择有关。
§5–1 空间任意力系向一点的简化· 主矢和主矩
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系：作用线在空间任意分布的力系。
空间汇交力系
空间任意力系
空间力偶系
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系：作用线在空间任意分布的力系。 一、空间任意力系向一点的简化
其中，各 Fi Fi ，
Fx 0, FAx Fx 0 (1) Fy 0, FAy Fy 0 (2) Fz 0, FAz Fz 0 (3) M x ( F ) 0, M y ( F ) 0, M z ( F ) 0,
FAz MAz
O
z
MAy FAx
FAy Fz
y 200 Fy
MAx
M Ax 0.075Fz 0 M Ay 0.2 Fz 0
x 75 Fx
M Az 0.075Fx 0.2 Fy 0
P 20 kN
§5–2 空间任意力系的平衡条件
解题步骤、技巧与注意问题： 1、解题步骤： ①选研究对象
O
11
§5–1 空间任意力系向一点的简化· 主矢和主矩
三、补充:空间任意力系的简化结果分析（最后结果）
空间力系的简化
F
MO
O
主矩： M O M O
x FR
FR
A
F1 3 m G1 1.5 m G2 3.9 m 2 355 kN m
y FR
2 2 F F ( F ) ( F ) 709.4 kN R x y 合力FR的大小： R
FR M B 50(i k ) 2.5i d 0.025 j 2 FR 5000
中心轴位置:
最后结果： FR 与 M B 组成的力螺旋。
例2：图示平面力系，已知：F1=F2=F3=F4=F，M=Fa，a为三 角形边长，若以A为简化中心，试求简化的最后结果，并在图 中画出。 解： 力系向A点简化
合成的结果必定是一个合力，这个合力指向被约束物 体，是一个压力 FN
未知量：3个
三、光滑铰链约束
（1） 球铰
FAz
A
FAx
FAy
约束力分布在一部分球面上，分布力均通过球心，构 成一空间汇交力系系，可简化为一个通过球心的合力 FR 球铰的约束力 FR 的大小与方向均未知，通常用沿直角
坐标分解的三个分量： FR x , FR y , FR z
(MO rOA FR ) FR MO FR M A FR
主矢与主矩的点积也与简化中心的选择无关，称之为力 系的第二不变量 由主矢与主矩的点积是否为零，就可判定出简化的最终 是合力还是力螺旋。
特例：平面任意力系的简化
F1 A1 A2
基本力系的简化结果：
汇交力系—过汇交点的合力
力偶系—合力偶
根据力的空间位臵：
空间力系、平面力系
MO
O
主矩： M O M O
x FR
FR
A
F1 3 m G1 1.5 m G2 3.9 m 2 355 kN m
y FR
2 2 F F ( F ) ( F ) 709.4 kN R x y 合力FR的大小： R
FR M B 50(i k ) 2.5i d 0.025 j 2 FR 5000
中心轴位置:
最后结果： FR 与 M B 组成的力螺旋。
例2：图示平面力系，已知：F1=F2=F3=F4=F，M=Fa，a为三 角形边长，若以A为简化中心，试求简化的最后结果，并在图 中画出。 解： 力系向A点简化
合成的结果必定是一个合力，这个合力指向被约束物 体，是一个压力 FN
未知量：3个
三、光滑铰链约束
（1） 球铰
FAz
A
FAx
FAy
约束力分布在一部分球面上，分布力均通过球心，构 成一空间汇交力系系，可简化为一个通过球心的合力 FR 球铰的约束力 FR 的大小与方向均未知，通常用沿直角
坐标分解的三个分量： FR x , FR y , FR z
(MO rOA FR ) FR MO FR M A FR
主矢与主矩的点积也与简化中心的选择无关，称之为力 系的第二不变量 由主矢与主矩的点积是否为零，就可判定出简化的最终 是合力还是力螺旋。
特例：平面任意力系的简化
F1 A1 A2
基本力系的简化结果：
汇交力系—过汇交点的合力
力偶系—合力偶
根据力的空间位臵：
空间力系、平面力系
力系的简化和平衡
空间汇交力系可合成一合力F'R:
z MO O x F'R y
FR Fi Fi
力系中各力的矢量和称为空间力系的 主矢。主矢与简化中心的位置无关。
空间力偶系可合成为一合力偶, 其矩矢MO:
MO MO (Fi )
力系中各力对简化中心之矩矢的矢量和称为力系对简化 中心的主矩。主矩与简化中心的位置有关。
3.1.2 (空间任意)力系向一点的简化 结论: 空间力系向任一点O简化, 可得一力和一 力偶, 这个力的大小和方向等于该力系的主矢, 作用线通过简化中心O; 这个力偶的矩矢等于该 力系对简化中心的主矩。
空间任意力系向一点简化的结果可能出现四种情况: (1) F'R＝0, MO≠0 ; (2) F'R ≠ 0, MO ＝ 0 ; (3) F'R ≠ 0, MO≠0 ;
′ Fn
O Mn
3.1.2 (平面任意)力系向一点简化 平面一般力系中各力的矢量和称为平面一般力 系的主矢。主矢与简化中心的位置无关。
FR FRx + FRy Fx i Fy j
FR ( Fx ) 2 ( Fy ) 2
Fx cos( FR , i ) FR Fy cos( FR , j ) FR
A
m
B q C
FAy
FB
求得的FAx和FAy为负, 说明与图中 假设方向相反。
例: 求图示刚架的约束反力。
P
A
解: 以刚架为研究对象, 受力如图。
a
q b
Fx 0 : FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
1 2 M A Pa qb 0 2
z MO O x F'R y
FR Fi Fi
力系中各力的矢量和称为空间力系的 主矢。主矢与简化中心的位置无关。
空间力偶系可合成为一合力偶, 其矩矢MO:
MO MO (Fi )
力系中各力对简化中心之矩矢的矢量和称为力系对简化 中心的主矩。主矩与简化中心的位置有关。
3.1.2 (空间任意)力系向一点的简化 结论: 空间力系向任一点O简化, 可得一力和一 力偶, 这个力的大小和方向等于该力系的主矢, 作用线通过简化中心O; 这个力偶的矩矢等于该 力系对简化中心的主矩。
空间任意力系向一点简化的结果可能出现四种情况: (1) F'R＝0, MO≠0 ; (2) F'R ≠ 0, MO ＝ 0 ; (3) F'R ≠ 0, MO≠0 ;
′ Fn
O Mn
3.1.2 (平面任意)力系向一点简化 平面一般力系中各力的矢量和称为平面一般力 系的主矢。主矢与简化中心的位置无关。
FR FRx + FRy Fx i Fy j
FR ( Fx ) 2 ( Fy ) 2
Fx cos( FR , i ) FR Fy cos( FR , j ) FR
A
m
B q C
FAy
FB
求得的FAx和FAy为负, 说明与图中 假设方向相反。
例: 求图示刚架的约束反力。
P
A
解: 以刚架为研究对象, 受力如图。
a
q b
Fx 0 : FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
1 2 M A Pa qb 0 2
3-4空间任意力系向一点简化.主矢和主矩
空间任意力系向一点的简化空间任意力系的简化结果分析空间任意力系向一点的简化·主矢和主矩空间任意力系向一点的简化)( ; 'i O i i i F M M F F ==空间任意力系等效转化为空间汇交力系和空间力偶系。
力的平移定理 空间汇交力系的合力kF j F i F F F iz iy ix i R Σ+Σ+Σ=Σ='— 力系的主矢空间力偶系的合力偶矩 )(i O i O F M M M Σ=Σ=— 空间力偶系的主矩 由力对点的矩与力对轴的矩的关系，有kF M j F M i F M M i z i y i x O )()()(Σ+Σ+Σ=简化结果：过简化中心的合力 00'=≠O R M F ，简化结果：不过简化中心的合力O R O R M F M F ⊥≠≠''00，，RO F M d ||= 空间任意力系的简化结果分析(1) 合力(2) 合力偶简化结果：合力偶，此时主矩与简化中心的位置无关00'≠=O R M F ，空间任意力系的简化结果分析(3) 力螺旋简化结果：过简化中心的力螺旋O R O R M F M F //00''，，≠≠右螺旋 左螺旋空间任意力系的简化结果分析(3) 力螺旋简化结果：不过简化中心的力螺旋成任意角与O R O R M F M F ''00，， ≠≠'sin RO F M d θ=(4) 平衡 00 '==O R M F ，— 空间任意力系平衡有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）空间任意力系向一点的简化空间任意力系的简化结果分析合力、合力偶、力螺旋、平衡空间任意力系向一点的简化·主矢和主矩 k F j F i F F F iz iy ix i R Σ+Σ+Σ=Σ='主矢 )(i O i O F M M M Σ=Σ=主矩 有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
空间平行力系的平衡方程，设各力线都 // z 轴。 因为 mz ( F ) 0 Z 0 X 0 m x ( F ) 0 Y 0 m y ( F ) 0
均成为了恒等式。
2、空间约束
观察物体在空间的六种（沿三轴移动和绕三轴转动）可能 的运动中，有哪几种运动被约束所阻碍，有阻碍就有约束反力。
所以空间任意力系的平衡方 0,m y ( F ) 0 Z 0,m z ( F ) 0
还有四矩式，五矩式和六矩式， 同时各有一定限制条件。
空间汇交力系的平衡方程为：
X 0 Y 0 Z 0
因为各力线都汇交于一点，各轴都通过 该点，故各力矩方程都成为了恒等式。
§5-2 空间任意力系的平衡条件
1、空间任意力系的平衡充要条件是： R '0 F 0 MO mO ( Fi )0
又 R ' ( X ) 2 ( Y ) 2 ( Z ) 2
M O ( m x ( F )) 2 ( m y ( F )) 2 ( m z ( F )) 2
阻碍移动为反力，阻碍转动为反力偶。[例]
1）球形铰链 （前面讲过）
球形铰链
2）向心轴承，滚珠(柱)轴承
绕x和z轴的转动 也同时被约束。
3）滑动轴承
4）止推轴承
第9页，加 两个绕轴 转动的约 束。
5）带有销子的夹板
6）空间固定端
作业：
自学教材例题5-1~5-4.