2010年东北大学数学建模培训模拟竞赛题
2010数学建模与计算机模拟题目

数学建模与计算机模拟题目8、政府中的腐败与一宗重大的政府丑闻的有牵连人数的增加率与早已牵连进去的人数和有关而尚未牵连进去的人数的乘积成正比。
假设当华盛顿的报纸将这一丑闻公诸于众时,有牵连人数为7人,3个月后有牵连人数增加了9人,又过了3个月后有牵连人数增加了12人。
与该丑闻有关的人数大概有多少人?请写出建立的模型及用matlab或者公式推导出来的结果。
9、某城市1990年的人口密度近似为,表示距市中心r公里区域内的人口数,单位为每平面公里10万人。
(1)试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
(2)若人口密度近似为(单位不变),试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
10、梵塔问题:传说中认为是世界中心的现印度北方邦瓦拉西纳县的一座大庙的穹顶的下面放有一个黄铜盘子,盘子上有三根钻石柱子,在其中一根柱子上套有64个大小不同的中空的纯金盘子(称为梵塔),且按上小下大的次序排列。
该庙的和尚按梵天(印度教大神之一)的法令昼夜不停地、每秒把一个盘子移到没有盘子的柱子上去,或者放到比它大的盘子的上面,传说,如果一旦把64个纯金盘子组成的梵塔按原样移到另两根钻石柱子中的任意一根时,世界末日就要到了,问和尚们要用多少时间才能完成,世界末日会来临吗?11、在市场经济中存在这样的循环现象,若去年的猪肉生产量供过于求,猪肉的价格就会降低,价格降低会使今年养猪者减少,使今年猪头供不应求,于是肉价上扬,价格上扬又使明年猪肉产量增加造成新的供过于求。
据统计,某城市1991年的猪头产量为30万吨,肉价为6.00元/公斤,1992年生产猪肉25万吨,肉价为8.00元/公斤,已知1993年的猪肉产量为28万吨。
若维持目前的消费水平与生产模式,并假定猪肉产量与价格之间是线性关系,问若干年以后猪肉的生产量与价格是否会趋于稳定?若能够稳定,请求出稳定的生产量和价格。
2010年数学建模集训小题目
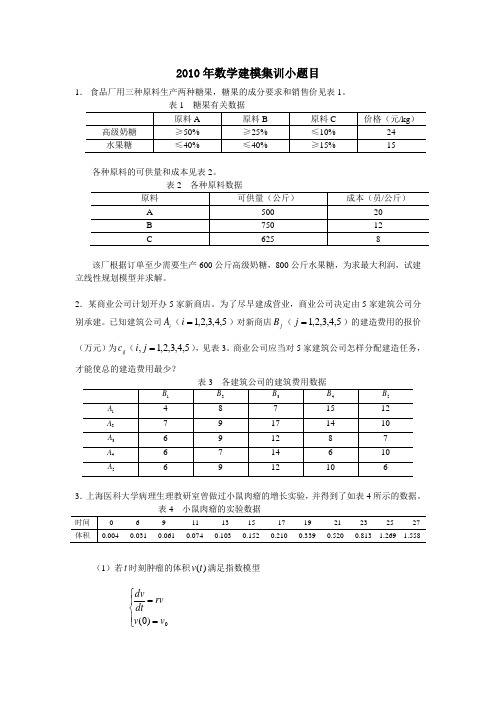
2010年数学建模集训小题目1. 食品厂用三种原料生产两种糖果,糖果的成分要求和销售价见表1。
表1 糖果有关数据各种原料的可供量和成本见表2。
该厂根据订单至少需要生产600公斤高级奶糖,800公斤水果糖,为求最大利润,试建立线性规划模型并求解。
2.某商业公司计划开办5家新商店。
为了尽早建成营业,商业公司决定由5家建筑公司分别承建。
已知建筑公司i A (5,4,3,2,1=i )对新商店j B (5,4,3,2,1=j )的建造费用的报价(万元)为ij c (5,4,3,2,1,=j i ),见表3。
商业公司应当对5家建筑公司怎样分配建造任务,才能使总的建造费用最少?3.上海医科大学病理生理教研室曾做过小鼠肉瘤的增长实验,并得到了如表4所示的数据。
(1)若t 时刻肿瘤的体积)(t v 满足指数模型⎪⎩⎪⎨⎧==0)0(v v rvdtdv请拟合参数r 。
(2)若t 时刻肿瘤的体积)(t v 满足Logistic 模型⎪⎩⎪⎨⎧=-=02)0(v v vv dtdv βα 请拟合参数βα,。
4.已知数据见表5。
试求y 对321,,x x x 的线性回归方程并检验回归效果,能否剔除一个变量?5.炼钢厂出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀作用,随着使用次数的增加,容积不断增大,实测得到15组数据如表6。
试分别按以下两种形式建立y 对x 的回归方程,画出散点图和回归曲线,并根据适当的指标判断哪一种好。
(1)xb a y +=1; (2)xbce y =.6.已知数据见表7。
试求形式为x a x a x a a y sin 332210+++=的回归方程并检验回归效果。
7.一枚导弹,以初始速度0v ,水平夹角α离开原点)0,0(。
如果导弹在),(e e y x 点着陆,且在飞行中受到一拉力,其大小和速度的平方成比例,那么控制导弹飞行轨迹的四个一阶方程为⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==++-=+-=x xy x yx y d y y x d x vdx dt vv dx dy v v v v c g dxdv v v c dx dv 12222 其中y 是导弹的垂直高度,x 是飞行的水平距离,t 是时间,x v 和y v 分别是速度v 的水平和垂直分量,d c 是拉力系数,g 是重力加速度。
东北三省数学建模竞赛历年赛题

东北三省数学建模竞赛历年赛题2006 A:油田开发规划的合理编制问题
B:冬季北方室内空气交换问题
C:中国人口政策问题
2007 A:油田开发规划的合理编制问题
B:冬季北方室内空气交换问题
C:中国人口政策问题
2008 A:滑雪场定价问题
B:居民楼顶最佳保温层厚度
C:灾区物资分配问题
2009 A:运动界面追踪
B:丁克与人口增长
C:客观、合理的评价学生学习状况
2010 A:企业的营销管理问题
B:走遍全中国
C:封闭系统的货币分布问题
2011 A:食品质量安全抽样数据分析
B: 垃圾分类处理与清运方案设计
C:水资源短缺风险评价
D:用出租车GPS数据分析深圳道路交通情况
2012 A:深圳人口与医疗需求预测模型
B:手机用户精准识别
C:绿色机房模型评价与控制
D:打孔机生产效能的提高
2013 A:食品质量安全抽检数据分析
B:深圳关内外交通拥堵探究与治理
C:垃圾减量分类活动中社会及个体因素的量化分析
D:自然灾害保险问题的研究
2014 A:计划生育政策调整对人口数量、结构及其影响的研究B:基因组组装
C:垃圾焚烧厂的经济补偿问题
D:以深圳市为例探讨洪灾损失预测研究的科学性与严谨性2015 A:医保欺诈行为的主动发现
B:DNA序列的k-mer index 问题
C:福田红树林自然保护区湿地生态系统研究
D: 航班延误问题。
2010数学建模与计算机模拟题目

数学建模与计算机模拟题目8、政府中的腐败与一宗重大的政府丑闻的有牵连人数的增加率与早已牵连进去的人数和有关而尚未牵连进去的人数的乘积成正比。
假设当华盛顿的报纸将这一丑闻公诸于众时,有牵连人数为7人,3个月后有牵连人数增加了9人,又过了3个月后有牵连人数增加了12人。
与该丑闻有关的人数大概有多少人?请写出建立的模型及用matlab或者公式推导出来的结果。
9、某城市1990年的人口密度近似为,表示距市中心r公里区域内的人口数,单位为每平面公里10万人。
(1)试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
(2)若人口密度近似为(单位不变),试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
10、梵塔问题:传说中认为是世界中心的现印度北方邦瓦拉西纳县的一座大庙的穹顶的下面放有一个黄铜盘子,盘子上有三根钻石柱子,在其中一根柱子上套有64个大小不同的中空的纯金盘子(称为梵塔),且按上小下大的次序排列。
该庙的和尚按梵天(印度教大神之一)的法令昼夜不停地、每秒把一个盘子移到没有盘子的柱子上去,或者放到比它大的盘子的上面,传说,如果一旦把64个纯金盘子组成的梵塔按原样移到另两根钻石柱子中的任意一根时,世界末日就要到了,问和尚们要用多少时间才能完成,世界末日会来临吗?11、在市场经济中存在这样的循环现象,若去年的猪肉生产量供过于求,猪肉的价格就会降低,价格降低会使今年养猪者减少,使今年猪头供不应求,于是肉价上扬,价格上扬又使明年猪肉产量增加造成新的供过于求。
据统计,某城市1991年的猪头产量为30万吨,肉价为6.00元/公斤,1992年生产猪肉25万吨,肉价为8.00元/公斤,已知1993年的猪肉产量为28万吨。
若维持目前的消费水平与生产模式,并假定猪肉产量与价格之间是线性关系,问若干年以后猪肉的生产量与价格是否会趋于稳定?若能够稳定,请求出稳定的生产量和价格。
2010年数学建模集训小题目解答.pdf1

生产 3 种产品的总利润为
综上所述,建立如下的线性规划模型
max
2 3 5 c x ∑ i ∑ ij − ∑∑ b j a ij xij i =1 j =1 i =1 j =1
3
s.t.
∑a
i =1
3
ij
xij ≤ d j , j = 1,2,L ,5
x11 + x12 = x13 + x14 + x15
3.某商业公司计划开办 5 家新商店。为了尽早建成营业,商业公司决定由 5 家建筑公司分
别承建。已知建筑公司 Ai ( i = 1,2,3,4,5 )对新商店 B j ( j = 1,2,3,4,5 )的建造费用的报价 , 见表 4。 商业公司应当对 5 家建筑公司怎样分配建造任务, (万元) 为 cij( i, j = 1,2,3,4,5 ) 才能使总的建造费用最少? 表 4 各建筑公司的建筑费用数据
解:用 j = 1,2,3,4 分别表示甲、乙、丙、丁四个企业, cij 表示第 i ( i = 1, L ,6 )台设备分 配给第 j 个企业创造的利润,引进 0 − 1 变量
1, 第i台设备分配给第j个企业 xij = , i = 1, L ,6 , j = 1,2,3,4 0, 第i台设备不分配给第j个企业
数学规划的 LINGO 程序:
model: sets: chanpin/1..3/:c; shebei/1..5/:b,d; link(chanpin,shebei):a,x; endsets data: c=1 1.65 2.3; a=@file('data1.txt'); b=@file('data1.txt'); d=@file('data1.txt'); enddata max=@sum(chanpin(i):c(i)*@sum(shebei(j)|j#le#2:x(i,j)))-@sum(chanpin( i):@sum(shebei(j):b(j)*a(i,j)*x(i,j))); @for(shebei(j):@sum(chanpin(i):a(i,j)*x(i,j))<d(j)); @sum(shebei(i)|i#le#2:x(1,i))=@sum(shebei(i)|i#ge#3:x(1,i)); x(2,1)+x(2,2)=x(2,3); x(3,2)=x(3,4); x(2,4)=0; x(2,5)=0; x(3,1)=0; x(3,3)=0; x(3,5)=0; end
第二届(2010年)全国大学生数学竞赛预赛试卷及参考答案(非数学类).docx

第二届(2010年)全国大学生数学竞赛预赛试卷及参考答案(非数学类)(150分钟)一、(25分,每小题5分)(1)设£ = (1 +。
)(1 + /)•••(】 + a,"),其中|a|< 1,求limxn->xi、L(2)求lime"A 1+— o"I x)(3)设5>0 ,求/ = f X e^xx x ll dx(n = 1,2,.. j oJo(4)设函数/(/)有二阶连续导数,r = y/x2 + y2,y) = f一\r)⑸求直线述了。
与直线A字二宁弓的距离。
解:(1) £=(1 +。
)(1 + /)…(1 +旷)=兀=(1一。
)(1 + 0)(1 + /)・・・(1 + 旷)/(1-6/)=(1—cr)(1 + )・・・(1+)/(1—a)=・・・=(1—)/(1—a)・•. liinx 1HII(1 - ah) / (1 - a) = 1 / (1 - a) /?-^x⑵lim厂A->X 1+丄I X)f 1 2lnr"* (1+—)r x2 ln<l+—) -x =lim^ -r = limeA->X .V->X令x=l/t,则UnU+f)-f)原式=lime z: = lime 21 fTO fTO =lin* 丽77 =产/TO(3)/” = f 宀”故=(-|)f x"de~sx =(-》[x”严I; -J;严X]=(4)略(不难,难得写)(5)用参数方程求解。
答案好像是二、(15分)设函数/(X)在(-8,乜)上具有二阶导数,并且f\x) > 0, lim f\x) = a > 0, lun f\x) = 0 v 0,且存在一点x0,使得/(x0) < 0。
A->-X证明:方程/(x) = 0在(YO、*O)恰有两个实根。
解:(简要过程) 二阶导数为正,则一阶导数单增,f(x)先减后增,因为f(x)有小于0的值,所以只需在两边 找两大于0的值。
2010东北三省数学建模

周游先生退休后想到各地旅游。计划走遍全国 的省会城市、直辖市、香港、澳门、台北。请 你为他按下面要求制定出行方案: 1.按地理位置(经纬度)设计最短路旅行方案; 2.如果2010年5月1日周先生从哈尔滨市出发, 每个城市停留3天,可选择航空、铁路(快车卧 铺或动车),设计最经济的旅行互联网上订票 方案; 3. 要综合考虑省钱、省时又方便,设定你的评 价准则,建立数学模型,修订你的方案; 4.对你的算法作复杂性、可行性及误差分析; 5.关于旅行商问题提出对你自己所采用的算法 的理解及评价。
最省钱的路径
周游先生引发的思考
最短路
最经济
综合考虑 省时、省钱
旅网的拓扑结构指的是组成网络的基本单元之间 的相互连接关系,网络的衔接结构包括任何一个 基本单元和其他基本单元之间的关系和整个网络 之间的关系所呈现的路线特性。
旅游低碳是指旅行商在综合考虑省钱、省时因素, 所最终达到让旅行商满意的状态。该项指标对于 整个旅网线路的选择有着较大的意义。 旅游网络领域内很多是解决最短路的问题,对低 碳的研究还处于表面阶段。该模型提出旅网拓扑 低碳评价准则,利用该准则界定旅网中的关键线 路,与此该准则也可以评价整个网络的低碳评价 准则。
模拟退火
最优化三大理论 经典算法
遗传算法
神经网络
TSP问题
旅行商问题TSP (Traveling Salesman Problem) 是指 已知n 个城市之间的相互距离,现有一推销员必须 遍访n 个城市,并且每个城市只能访问一次,最后 又必须返回出发城市。如何安排访问次序,才可 以使其旅行路线的总长度最短 ,这是一个典型的 组合优化问题,并且是一个NP 难题,所以一般很难 精确的求出其最优解。而1983 年由Kirkpatrick 等 人提出的按统计方式工作的机器与组合最佳化问 题有着深刻意义的联系 ,这成功的将退火思想引 入了组合最优领域。
2010数学建模竞赛A B题 高教社杯全国大学生数学建模竞赛题目

2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
草根分享论坛 图吧 分享吧 海之南 分享斑竹 share8 好学吧附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子 出油管油位探测装置 注油口 检查口地平线 2m 6m 1m 1m3 m油位高度 图1 储油罐正面示意图 油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线α油油浮子出油管油位探针注油口水平线1.2m1.2m1.78m图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线 油3m油2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年东北大学数学建模培训模拟竞赛试题
问题-A海潮和泄洪
近年来世界范围的气候情况发生了巨大的变化,极端气候出现频率大大增加,百年未遇的自然灾害每年都有极大可能发生。
其原因可能是由于:全球气候变暖、温室气体排放增多以及人类生产活动破坏了地表植被等原因造成的。
据国家减灾委、民政部的统计,截至8月6日,今年洪涝灾害造成全国2亿人(次)受灾,1454人死亡,669人失踪,1214.8万人(次)紧急转移安置,1347.1万公顷农作物受灾,其中209万公顷绝收,136.4万间房屋倒塌,358.1万间房屋损坏,因灾直接经济损失2751.6亿元。
给人民生命和财产造成了巨大损失。
2010年8月7日夜22点左右舟曲发生的特大洪水泥石流损失更是令人触目惊心!
我国已经建立的一些水利设施在防洪减灾方面起到了很大作用。
三峡工程的作用主要有:发电、防洪、灌溉,首要任务是防洪。
连日来,三峡大坝及时挡水控泄,发挥重要的防洪作用。
截至14日,三峡已接受长江防总发出的11次调度令,或增大出库流量以腾出库容应对上游来水,或减少出库流量以缓解下游防汛压力。
长江下游的中心城市上海是我国重要的经济中心,其防洪任务非常艰巨和重要。
现在主要考虑海水和长江对上海的影响。
海水主要有由天体引潮力所引起的潮汐的天文潮和由于风暴的强风作用而引起港湾水面急速异常升高的风暴潮。
长江主要是上游洪水引起的。
当三种情况出现叠加(或两种叠加)就有可能造成上海的洪水施虐。
建立数学模型:
(1)分析上海是否会出现被洪水淹没的可能性;
(2)调控三峡大坝的泄洪量可以使得上海防洪压力减轻,设计一个算法,在大坝设施安全的
前提下,根据海水的影响调整三峡大坝的泄洪量以确保上海市的安全并且不影响生产和生活。
问题-B车间打磨机的效率问题
某个单位的车间工人上班时间为早8:00-16:00,中间没有休息时间。
此车间前一段时间花费了1万元购置了一台工具打磨机,工人的生产工具出现问题,必须中断生产前来打磨工具。
表1是一段时间内20个工人打磨情况的记录。
按照打磨技术水平要求,平均每15分钟打磨一件工具车间须花费100元,如果想缩短时间,需要提高打磨机辅助用品质量,每一件工具打磨时间缩短1分钟需要多花费10元。
对于整个车间,平均每个工人中断生产1分钟,车间效益将损失若干元
(1) 建立数学模型分析该车间是否应该另外添置一台打磨机?
(2) 现在车间要求达到平均两个小时内只有一人在等候打磨,利用所建模型分析此要求是否可行,车间需要支出费用多少?
(3) 车间为了确保整个生产安全有序地进行,就要让在打磨间的人数尽量少于2人,利用所建模型分析此要求是否能够实现,车间需要支出费用多少?
(4) 如果在16:00打磨机停止工作,多少工人可以提前多长时间下班?现在该车间想调整作息时间为8:00-12:00,13:00-17:00,打磨机工作时间为8:00-17:00,模型应该如何调整?
大学生数学建模竞赛论文格式规范和规则
参赛队从A、B题中任选一题。
1.论文用白色A4纸单面打印;上下左右各留出至少2.5厘米的页边距;从左侧装订。
2.论文的第一页为封面页(本文档最后一页),将三个参赛队员的按学号姓名班级填入封面横线内,在你选择的题目前保留√号即可。
3.论文题目和摘要写在论文第二页上,从第三页开始是论文正文。
4.论文的正文页数不超过20页。
5.论文从第三页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号。
6.论文不能有页眉,论文中不能有任何可能显示答题人身份的标志。
7.论文题目用三号黑体字、一级标题用四号黑体字,并居中。
论文中其他汉字一律采用小四号宋体字,行距用单倍行距,打印时应尽量避免彩色打印。
8.提请大家注意:摘要应该是一份简明扼要的详细摘要(包括关键词),在整篇论文评阅中占有重要权重,请认真书写(注意篇幅不能超过一页,且无需译成英文)。
评阅时将首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选。
9.引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
解答过程中使用的数据不得引用文献类型(1)(2)(3)(4)中出现的数据,引用数据必须表明出处。
各类文献的表述格式如下(其它类型文献不得引用):
(1)专著格式:
序号. 编著者1,编著者2,编著者3等. 书名[M]. 出版地:出版社,年代:页码.
(2)期刊论文格式:
序号. 编著者1,编著者2,编著者3等. 论文名称[J]. 期刊名称,年度,卷(期):起止页码.
(3)会议论文格式:
序号. 编著者1,编著者2,编著者3等. 论文名称[C]//会议名称,会议举办地,年度,起止页码.
(4)学位论文格式:
序号. 编著者1,编著者2,编著者3等. 学位论文名称[D]. 发表地:学位授予单位,年度:页码.
(5)电子文献格式:
序号. 作者. 电子文献题名(电子文献及载体类型标识). 电子文献的出处或可获得地址,发表或更新日期/引用日期。
只考虑两种电子文献:
[DB/OL]—联机网上数据库(database online)
[EB/OL]—网上电子公告(electronic bulletin board online)
样例:
[1]Peitgen H O, Jurgens H, Saupe D. Chaos and fractals[M]. Berlin: Springer-Verlag,
1992:202-213.
[2]Zhao Shi, Wang Yi-ding, Wang Yun-hong. Extracting hand vein patterns from low-quality
images: a new biometric technique using low-cost devices[C]// Fourth International Conference on Image and Graphics. Sichuan, 2007:667-671.
[3]韩笑.人体手背静脉识别算法研究[D].长春: 吉林大学.2007:37-40.
[4]关于中国学术期刊标准化数据库系统工程的进展[EB/OL].
/pub/wml.txt/980810-2.html,1998-08-16/1998-10-04.
当作者人数多于三人时,只列出前三位,并在第三作者后加“等”或“et al” 。
参考文献中标点符号格式严格按照样例所示。
参考文献采用顺序号编号体系。
参考文献的引用,必须在引用语句或段落的末尾处,用右上角标明所引参考文献的序号,并用“[]”括起文献序号。
如同时引用文献数量为2个,采用形如“…...[7,8]。
”的格式。
当引用文献数量超过3个时,采用形如“…...[11-15]。
”的格式。
参考文献的排序应按照其在正文中被引用的先后次序排号。
10.以下情况视为无效答卷,答卷作废:
1) 无自己建立的数学模型
数学建模活动的意义在于建立自己的模型而非使用现成模型解决问题,问题的解决是依赖他人的模型而非自己建立的模型,即使问题解决了也偏离了数学建模的初衷。
2) 抄袭;
3) 试卷雷同;
4) 提供的参考文献,查不到;
5) 关键引用处不标注;
6) 没有注明使用的数据的出处。
11.比赛结束后,对于获得进入决赛资格的人员名单进行公示,如发现有违规行为,可以匿名和实名方式进行举报,一经查实即取消相应资格。
12.比赛结束后上交纸质和相关电子文档各一份,电子文档以第一个队员的学号为文件夹名,文件夹中包括:电子答卷、实现的程序源代码、引用的文献(缺一不可!),电子文档为使用word2003及以下版本(后缀非docx)。
20日中午12点前将所需材料交到信息楼515,过时不侯!
本规范的解释权属于东北大学创新中心
2010-8-17
2010年东北大学数学建模培训模拟竞赛参赛队:学号姓名班级
选择题目:√A √B
东北大学大学生创新中心。
