匈牙利算法示例ppt
图论课件--匈牙利算法与最优匹配算法(精选)共34页PPT
11、不为五斗米折腰。 12、芳菊开林耀，青松冠岩列。怀此 贞秀姿 ，卓为 霜下杰 。
13、归去来兮，田蜀将芜胡不归。 14、酒能祛百虑，菊为制颓龄。 15、春蚕收长丝，秋熟靡王税。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪29、勇猛、大胆和坚定的 Nhomakorabea心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
34
匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。
美国数学家哈罗德·库恩于1955年提出该算法。
此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。
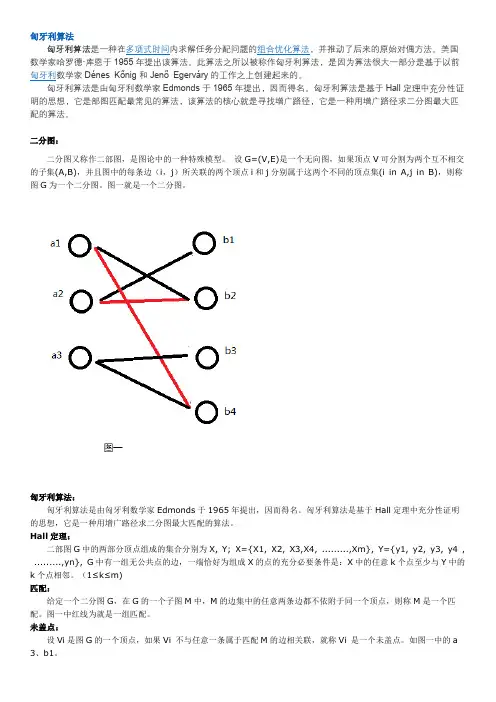
二分图：二分图又称作二部图，是图论中的一种特殊模型。
设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。
图一就是一个二分图。
匈牙利算法：匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想，它是一种用增广路径求二分图最大匹配的算法。
Hall定理：二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边，一端恰好为组成X的点的充分必要条件是：X中的任意k个点至少与Y中的k个点相邻。
（1≤k≤m)匹配：给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
图一中红线为就是一组匹配。
未盖点：设Vi是图G的一个顶点，如果Vi 不与任意一条属于匹配M的边相关联，就称Vi 是一个未盖点。
如图一中的a 3、b1。
设P是图G的一条路，如果P的任意两条相邻的边一定是一条属于M而另一条不属于M，就称P是一条交错路。
匈牙利算法示例ppt
•
非标准型的指派问题：
匈牙利法的条件是：模型求最小值、效率cij≥0。 当遇到各种非标准形式的指派问题时，处理方法是先将 其转化为标准形式， 1、人数和事数不相等的指派问题：人少事情多，虚拟 “人”，做各事的费用系数为0；人多事情少，虚拟 “事”，各人做的费用系数为0。 2、对于求极大化的问题，只要系数矩阵变换为B＝（mcij）nn，仍可利用匈牙利算法进行求解。 3、一个人可以做几件事情的指派问题：可以将该人化 作相同的几个“人”来接受指派，费用一样。 4、某事一定不能由某人做的指派问题，费用系数为“ M” 然后用匈牙利法来求解。
2 0 2 4 5
-0 -0 -0 -0 -0
第二步：进行试指派，以寻求最优解。 在 (bij) 中找尽可能多的独立 0 元素，若能找出 n 个 独立 0元素，就以这 n个独立 0元素对应解矩阵 (xij)中的 元素为1，其余为0，这就得到最优解。找独立0元素， 常用的步骤为：
0 0 1 0 0
或
0 0 0 0 1
1 0 0 0 0
0 0 0 1 0
0 1 0 0 0
0 0 1 0 0
解矩阵得到2个最优指派方案；（1）甲-B，乙-C， 丙--E，丁-D,戊-A；（2）甲-B，乙-D，丙-E,丁-C， 戊-A。所需时间为minz=7+6+9+6+4=32
二分图匹配(匈牙利算法)
设G=(V,{R})是一个无向图。
如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。
则称图G为二分图。
v给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
v选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)v如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
最大匹配在实际中有广泛的用处，求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。
但是这个算法的复杂度为边数的指数级函数。
因此，需要寻求一种更加高效的算法。
匈牙利算法是求解最大匹配的有效算法，该算法用到了增广路的定义(也称增广轨或交错轨)：若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M 的一条增广路径。
由增广路径的定义可以推出下述三个结论：v 1. P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
v 2. P经过取反操作（即非M中的边变为M中的边，原来M中的边去掉）可以得到一个更大的匹配M’。
v 3. M为G的最大匹配当且仅当不存在相对于M的增广路径。
从而可以得到求解最大匹配的匈牙利算法：v(1)置M为空v(2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替Mv(3)重复(2)操作直到找不出增广路径为止根据该算法，我选用dfs (深度优先搜索)实现。
程序清单如下：int match[i] //存储集合m中的节点i在集合n中的匹配节点,初值为-1。
int n,m,match[100]; //二分图的两个集合分别含有n和m个元素。
bool visit[100],map[100][100]; //map存储邻接矩阵。
bool dfs(int k){int t;for(int i = 0; i < m; i++)if(map[k][i] && !visit[i]){visit[i] = true;t = match[i];match[i] = k; //路径取反操作。
最大匹配之匈牙利算法模板。。
最大匹配之匈牙利算法模板。
要学习匈牙利算法先要懂得二部图的各种概念。
下面给出由o( _ )o MiYu 总结的普通性概念，这些概念很重要，一定要懂。
二分图的基本概念: ( 意思就是全部的点分成了2个集合 x, y. 每个集合中的顶点互相间没有边 ) 一个无向图 G = V, E , 假如存在两个集合X, Y, 使得X Y=V, X Y= , 并且每一条边e={x, y} 有x X,y Y, 则称G为一个二分图(bipartite graph). 常用来表示一个二分图. 若对X中任一x 及Y中任一y 恰有一边e E, 使e = {x, y}, 则称G为彻低二分图(complete bipartite graph). 二分图的性质： ( 交叉轨和增广路的概念很重要 ) 定理：无向图G为二分图的充分须要条件是，G起码有两个顶点,且其全部回路的长度均为偶数. 匹配：设G=为二分图，假如M&be;E，并且M中没有任何两边有公共端点。
M= 时称M为空匹配. 盖点: 若M是二分图的一个匹配, 将M中的边多所关联的顶点称为盖点, 其余则为未盖点. 交叉轨: 若一条路径上属于M的边和不属于M 的边交替浮现, 则称该路径为交叉轨. 增广路径: 若路径 P 是一条起始点和尽头都是未盖点的交叉轨, 那么 P 称为 M 的增广路径. 最大匹配: G的全部匹配中边数最多的匹配称为最大匹配. 性质1 : 一条关于M的增广路径的长度必为奇数, 且路上的第一条边和最后一条边都不属于M.性质2 : 对于一条关于M的增广路径 P, 将M 中属于P的边删去, 将P中不属于M 的边添加到M中,所得到的边集合计为 M P, 则 M P 比 M 多一条匹配边.性质3 : M 为 G 的一个最大匹配当且仅当不存在关于M的增广路径.hall 定理 : 对于二分图 G = ( X, Y, E ) , 存在一个匹配M, 使得 X 的全部顶点关于M饱和的充要条件是: 对 X 的任一子集A , 对A邻接的点集为P (A), 恒有 : | P[A] | = | A |其中性质 2 和性质 3 和 hall 定理的充分性证实就是匈牙利算法的基础 .. 二分图的最小顶点笼罩 ==== 最大匹配 DAG图的最小路径笼罩数 == 节点数最大匹配数二分图的最大自立集数 = 节点数最大匹配数在二分图中求最少的点，让每条边都起码和其中的一第1页共2页。
匈牙利算法
12 7 9 7 9 7 89666 6 7 17 12 14 9 7 15 14 6 6 10 6 4 10 7 10 9 4
第23页
50202 23000 0 10 5 7 2 98004 06365
第24页
➢从只有一个0元素的行开始，给 这个0元素加圈，记
50202 23000
10 5 7 2
70202 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第49页
➢从只有一个0元素的列开始，给这个0 元素加圈，记
72 0 2 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第50页
然后划去所在的行的其他0元素，记 作Ø。
72Ø 2 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第11页
2 15 13 4 2 10 4 14 15 4 (cij)= 9 14 16 13 9 7 8 11 9 7
0 13 11 2
6 0 10 11
057 4
0 13 7 0 606 9
014 2 42
053 2
010 0
第12页
第二步：进行试分配，以寻找最优解。
➢从只有一个0元素的行（或列）开 始，给这个0元素加圈，记，然后 划去所在的列（或行）的其他0元 素，记作Ø。
第34页
对没有的行，打
52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
第35页
对已打行中所有含0元素的列打
52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
第36页
再对打列中含0元素的行打 52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
指派问题的匈牙利法ppt
确定调整行与列
在没有圈起得零所在行上打“√”; 在打“√”行中所有零所在得列打“√”; 在打“√”列中含有圈起零得行上打“√”, 反复执行2)与3)两步,直到不能打“√”为止; 用直线划去打“√”得列与不打“√”得行,没有
划去得行构成调整得行,划去得列构成调整列。
调整可行解得方法
在调整行中寻找最小得元素,将它作为调整 量;
将调整行各元素减去调整量,对调整列中各 元素加上调整量。
再次执行“圈零”与“划零”得操作,并循 环以上得步骤,直到圈起得零数等于n为止。
匈牙利法解例3、3
时间矩阵
2 10 3 7
15
4
14
8
13 14 16 11
4
7
13
任务
人员
A
B
C
D
甲
6
7
11
2
乙
4
5
9
8
丙
3
1
10
4
丁
5
9
8
2
求解过程如下:
第一步,变换系数矩阵:
6 7 11 2 2
(cij
)
4 3
5 1
9 10
8 4 4 1
5 9 8 2 2
4 5 9 0 0 1 5 4 2 0 9 3 3 7 6 0
4 5 4 0 0 1 0 4 2 0 4 3 3 7 1 0
0元素,就以这n个独立0元素对应解矩阵(xij)中得元素为1, 其余为0,这就得到最优解。找独立0元素,常用得步骤为:
(1)从只有一个0元素得行(列)开始,给这个0元素加圈, 记作◎ 。然后划去◎ 所在列(行)得其它0元素,记作Ø ; 这表示这列所代表得任务已指派完,不必再考虑别人了。
ppt19 匈牙利算法与最优匹配算法
y4
y5
(c) y2为M非饱和点，加上y2和边x3y2生长树H。此 时，置M=MΔE(P)=｛x1y1, x2y3, x3y2｝
x1 y2 x2 x3 x4 x5
x3
y1
y2
y3 G=(X, Y)
y4
y5 10
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
15
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
定义2 设G=(X, Y), 若对任意的x ∈X, y ∈Y,有：
l ( x ) l ( y ) w ( xy )
称 l 是赋权完全偶图G的可行顶点标号。 对于任意的赋权完全偶图G，均存在G的可行顶点标号。 事实上，设：
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
2) 若 T N (S ) 令y ∈N(S) – T, 则在树H中存在点x与y邻接。因为H的所有 点，除u外，均在M下配对。所以，或者x = u，或者x与H的某 xy M 一顶点配对，但无论哪种情况，都有
w ( M *)
eM *
w(e)
vV ( G )
l (v )
又设M是G的任一完美匹配，则：
w( M )
eM
w(e)
l (v )
vV ( G )
所以，w (M*)≥w (M)。即M*是G的最优匹配。
18
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
w ( xy ), 若 x X , l ( x ) max yY l ( y ) 0, 若 y Y .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C
D E F Nhomakorabea匈牙利算法
１
２ ３
A
B C
１
２ ３ ４ 5
A
B C D E F
１ ２
A B
３
４ 5
C
D E
４
5
D
E F
F
(1)找到某一匹配M (2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替M (3)重复(2)操作直到找不出增广路径为止
分配问题及其数学模型
有甲、乙、丙、丁、戊五 位工人被指派去完成A、B 、 C 、 D 、 E五项任务，每 个人完成任务所需的工时 各不相同，见表。求应如 何指派人员才能使得所用 工时最少？
二分图
设G=(V,{R})是一个无向图。图的顶点集V可分割为两个互不 相交的子集X和Y（子集内部没有边） ，图任何一条边的两个 端点都分属不同的子集。则称图G为二分图。 用n个顶点X={1,2,3,4,5}表示n个工作，用m个顶点 Y={A,B,C,D,E,F}表示m个工人。
A
B
C
D
E
F
{A,B,C,D,E,F}
2 0 2 4 5
-0 -0 -0 -0 -0
第二步：进行试指派，以寻求最优解。 在 (bij) 中找尽可能多的独立 0 元素，若能找出 n 个 独立 0元素，就以这 n个独立 0元素对应解矩阵 (xij)中的 元素为1，其余为0，这就得到最优解。找独立0元素， 常用的步骤为：
B C A B
C D E F
A
D
E
F
1
A B
2
C
3 D
4 E
5
F A
1 B
2 C
3 D
4
5
E
F
1
2
3
4
5
1
2
3
4
5
匈牙利算法
１
A
B
增广路的定义(也称增广轨或交错轨)：若P是图 G中一条连通两个未匹配顶点的路径，并且属 ２ M的边和不属M的边(即已匹配和待匹配的边)在 P上交替出现，则称P为相对于M的一条增广路 径。 ３ 由增广路的定义可以推出下述三个结论： 1）P的路径长度必定为奇数，第一条边和最后 ４ 一条边都不属于M。 2）P经过取反操作可以得到一个更大的匹配M’。 3）M为G的最大匹配当且仅当不存在相对于M 5 的增广路径。
7 ◎ 2 Ø 2 4 3 Ø Ø ◎ Ø 8 3 5 ◎ 11 8 4 ◎ Ø ◎ 4 1 4 3
上面矩阵有5个独立0元素，这就得到相应的最优解。
0 0 0 0 1
1 0 0 0 0
0 1 0 0 0
0 0 0 1 0
1
2
3
4
5
{1,2,3,4,5}
二分图匹配
给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两 条边都不依附于同一个顶点，则称M是一个匹配。在工作分配的问 题中，我们给出一个可行的分配方案，就是一个匹配。 选择这样的边数最大的子集称为图的最大匹配问题如果这个匹配是 最优的（可以填补的工作岗位最多），就是最大匹配。
5 0 2 0 2 3 0 0 0 10 5 7 9 8 0 0 0 6 3 6
2 0 2 4 5
5 2 ◎ 0 9 0 Ø
0 ◎ 3 10 8 6
2 Ø 0 2 0 Ø 0 ◎ 0 Ø 5 7 2 ◎ 0 Ø 0 4 3 6 5
5 2 ◎ 0 9 0 Ø √
0 2 0 ◎ Ø 2 3 Ø 0 0 0 Ø ◎ 10 5 7 2 √ 8 ◎ 0 0 Ø 4 6 3 6 5 √
第四步；在没有被直线覆盖的部分中找出最小元素。 然后在行打√行每个元素减去这一最小元素，而在打√ 列的每个元素都加上这一最小元素，以保证原来0元 素不变。这样得到新系数矩阵。若得到n个独立的0 元素，则已得到最优解，否则回到第三步。
(1)从只有一个0元素的行(列)开始，给这个0元素加圈，记作◎ 。然后划 去◎ 所在列(行)的其它0元素，记作Ø ；这表示这列所代表的任务已指派完， 不必再考虑别人了。 (2)给只有一个0元素的列(行)中的0元素加圈，记作◎；然后划去◎ 所在 行的0元素，记作Ø ． (3)反复进行(1)，(2)两步，直到尽可能多的0元素都被圈出和划掉为止。
5 2 ◎ 9 Ø
◎
3 10 8 6
2 Ø 2 Ø Ø ◎ 5 7 2 ◎ Ø 4 3 6 5
第三步；作最少的直线覆盖所有0元素，以确 定该系数矩阵中能找到最多的独立元素数。
（1）对没有◎的行打√ （2）在已经打√的行中所含有的0 元素打√号 （3）在已经打√号的列中含◎元 素的行打√； √ （4）重复（2）（3）直到得不出 打√的行列为止 （5）对没有打√的行画一横线， 有打√的列画一纵线，这就覆盖所 有0元素的最少直线数。令这一直 线数为l。若l<n,说明必须再换当 前的系数矩阵，才能找到n个独立 的0元素，为此转到第四步；若 l=n，而m<n，应回到（2）（4） 另行试探。
12 8 (cij ) 7 15 4
-7 -6 -7 -6 -4
5 0 2 0 2 3 0 0 0 10 5 7 9 8 0 0 0 6 3 6
2 0 2 4 5
5 0 2 0 2 3 0 0 0 10 5 7 9 8 0 0 0 6 3 6
•
非标准型的指派问题：
匈牙利法的条件是：模型求最小值、效率cij≥0。 当遇到各种非标准形式的指派问题时，处理方法是先将 其转化为标准形式， 1、人数和事数不相等的指派问题：人少事情多，虚拟 “人”，做各事的费用系数为0；人多事情少，虚拟 “事”，各人做的费用系数为0。 2、对于求极大化的问题，只要系数矩阵变换为B＝（mcij）nn，仍可利用匈牙利算法进行求解。 3、一个人可以做几件事情的指派问题：可以将该人化 作相同的几个“人”来接受指派，费用一样。 4、某事一定不能由某人做的指派问题，费用系数为“ M” 然后用匈牙利法来求解。
8
匈牙利算法的基本原理是基于以下两个定理. 定理1 设C=(Cij)n×n是指派问题的效益矩阵， 若将C中的任一行（或任一列）减去该行 （或该列）中的最小元素，得到新的效率矩 阵C’，则C’对应的新的指派问题与原指派问 题有相同的最优解. 定理2 效率矩阵C中独立的0元素的最多个数 等于覆盖所有0元素的最少直线数. 当独立零 元素的个数等于矩阵的阶数时就得到最优解.
9
匈牙利法的解题步骤：
第一步：变换指派问题的系数矩阵（cij）为 (bij)，使在(bij)的各行各列中都出现0元素，即 (1) 从（cij）的每行元素都减去该行的最小 元素； (2) 再从所得新系数矩阵的每列元素中减去 该列的最小元素。
7 9 7 9 9 6 6 6 17 12 14 9 14 6 6 10 10 7 10 9
匈牙利算法
经典问题——工作分配
一个公司有n个工作岗位空缺，每个岗位空 缺需要有一定资格的人来填补。现在有m个 人申请这n个工作。由于每个人工作能力不 同，所以不同的人能胜任不同的工作。 现在已知每个人所能胜任的若干工作，求 这m个人最多可以填补几个工作岗位。 每个人只能做一份工作，每个工作岗位也 只需要一个人
0 0 1 0 0
或
0 0 0 0 1
1 0 0 0 0
0 0 0 1 0
0 1 0 0 0
0 0 1 0 0
解矩阵得到2个最优指派方案；（1）甲-B，乙-C， 丙--E，丁-D,戊-A；（2）甲-B，乙-D，丙-E,丁-C， 戊-A。所需时间为minz=7+6+9+6+4=32
xi1 xi 2 xij xin 1 i=1,2, …,n s.t x1 j x2 j xij xnj 1 j=1,2, …,n xij 0,1 i 1,2,, n; j 1,2,, n
j i
min Z cij xij
5 2 ◎ 0 9 0 Ø
+2
√ ×
0 Ø 2 0 0 Ø ◎ 10 5 7 2 √ -2 8 ◎ 0 0 4 Ø 6 3 6 5 √ -2 0 2 ◎ 3 Ø 0
7 4 Ø 11 ◎
◎ 2 Ø 2 3 ◎ Ø Ø 8 3 5 ◎ 8 Ø ◎ 4 4 1 4 3
时 任 间 务 人员
A 12 8 7 15 4
B 7 9 17 14 10
C 9 6 12 6 7
D 7 6 14 6 10
E 9 6 9 10 9
甲 乙 丙 丁 戊
设有n个工作，要由 n个人 来承担，每个工作只能由一 个人承担，且每个人只能承 担一个工作。cij表示第i个人 做第j件事的费用,求总费用 最低的指派方案。
15
请各位老师和同学批评指导！