匈牙利算法示例ppt
匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。
美国数学家哈罗德·库恩于1955年提出该算法。
此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。
二分图：二分图又称作二部图，是图论中的一种特殊模型。
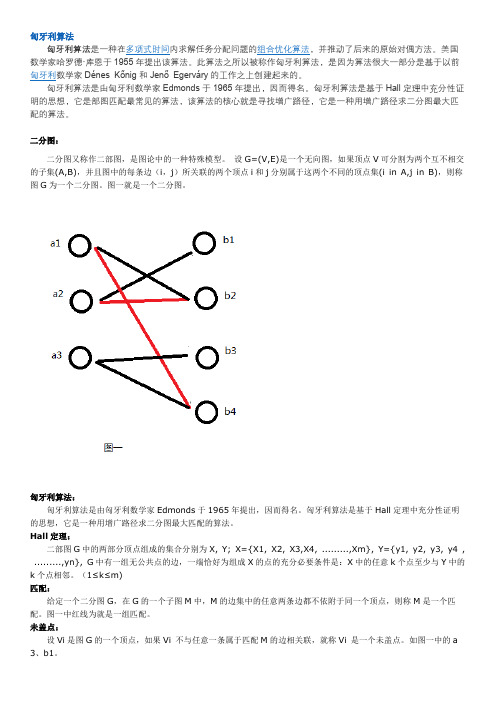
设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。
图一就是一个二分图。
匈牙利算法：匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想，它是一种用增广路径求二分图最大匹配的算法。
Hall定理：二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边，一端恰好为组成X的点的充分必要条件是：X中的任意k个点至少与Y中的k个点相邻。
（1≤k≤m)匹配：给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
图一中红线为就是一组匹配。
未盖点：设Vi是图G的一个顶点，如果Vi 不与任意一条属于匹配M的边相关联，就称Vi 是一个未盖点。
如图一中的a 3、b1。
设P是图G的一条路，如果P的任意两条相邻的边一定是一条属于M而另一条不属于M，就称P是一条交错路。
匈牙利算法示例ppt
•
非标准型的指派问题：
匈牙利法的条件是：模型求最小值、效率cij≥0。 当遇到各种非标准形式的指派问题时，处理方法是先将 其转化为标准形式， 1、人数和事数不相等的指派问题：人少事情多，虚拟 “人”，做各事的费用系数为0；人多事情少，虚拟 “事”，各人做的费用系数为0。 2、对于求极大化的问题，只要系数矩阵变换为B＝（mcij）nn，仍可利用匈牙利算法进行求解。 3、一个人可以做几件事情的指派问题：可以将该人化 作相同的几个“人”来接受指派，费用一样。 4、某事一定不能由某人做的指派问题，费用系数为“ M” 然后用匈牙利法来求解。
2 0 2 4 5
-0 -0 -0 -0 -0
第二步：进行试指派，以寻求最优解。 在 (bij) 中找尽可能多的独立 0 元素，若能找出 n 个 独立 0元素，就以这 n个独立 0元素对应解矩阵 (xij)中的 元素为1，其余为0，这就得到最优解。找独立0元素， 常用的步骤为：
0 0 1 0 0
或
0 0 0 0 1
1 0 0 0 0
0 0 0 1 0
0 1 0 0 0
0 0 1 0 0
解矩阵得到2个最优指派方案；（1）甲-B，乙-C， 丙--E，丁-D,戊-A；（2）甲-B，乙-D，丙-E,丁-C， 戊-A。所需时间为minz=7+6+9+6+4=32
指派问题的匈牙利法ppt
确定调整行与列
在没有圈起得零所在行上打“√”; 在打“√”行中所有零所在得列打“√”; 在打“√”列中含有圈起零得行上打“√”, 反复执行2)与3)两步,直到不能打“√”为止; 用直线划去打“√”得列与不打“√”得行,没有
划去得行构成调整得行,划去得列构成调整列。
调整可行解得方法
在调整行中寻找最小得元素,将它作为调整 量;
将调整行各元素减去调整量,对调整列中各 元素加上调整量。
再次执行“圈零”与“划零”得操作,并循 环以上得步骤,直到圈起得零数等于n为止。
匈牙利法解例3、3
时间矩阵
2 10 3 7
15
4
14
8
13 14 16 11
4
7
13
任务
人员
A
B
C
D
甲
6
7
11
2
乙
4
5
9
8
丙
3
1
10
4
丁
5
9
8
2
求解过程如下:
第一步,变换系数矩阵:
6 7 11 2 2
(cij
)
4 3
5 1
9 10
8 4 4 1
5 9 8 2 2
4 5 9 0 0 1 5 4 2 0 9 3 3 7 6 0
4 5 4 0 0 1 0 4 2 0 4 3 3 7 1 0
0元素,就以这n个独立0元素对应解矩阵(xij)中得元素为1, 其余为0,这就得到最优解。找独立0元素,常用得步骤为:
(1)从只有一个0元素得行(列)开始,给这个0元素加圈, 记作◎ 。然后划去◎ 所在列(行)得其它0元素,记作Ø ; 这表示这列所代表得任务已指派完,不必再考虑别人了。
ppt19 匈牙利算法与最优匹配算法
y4
y5
(c) y2为M非饱和点，加上y2和边x3y2生长树H。此 时，置M=MΔE(P)=｛x1y1, x2y3, x3y2｝
x1 y2 x2 x3 x4 x5
x3
y1
y2
y3 G=(X, Y)
y4
y5 10
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
15
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
定义2 设G=(X, Y), 若对任意的x ∈X, y ∈Y,有：
l ( x ) l ( y ) w ( xy )
称 l 是赋权完全偶图G的可行顶点标号。 对于任意的赋权完全偶图G，均存在G的可行顶点标号。 事实上，设：
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
2) 若 T N (S ) 令y ∈N(S) – T, 则在树H中存在点x与y邻接。因为H的所有 点，除u外，均在M下配对。所以，或者x = u，或者x与H的某 xy M 一顶点配对，但无论哪种情况，都有
w ( M *)
eM *
w(e)
vV ( G )
l (v )
又设M是G的任一完美匹配，则：
w( M )
eM
w(e)
l (v )
vV ( G )
所以，w (M*)≥w (M)。即M*是G的最优匹配。
18
1 0.5 n 0 0.5 1 2 1.5 t 1 0.5 0 0 0.2 0.4 x 0.6 0.8 1
w ( xy ), 若 x X , l ( x ) max yY l ( y ) 0, 若 y Y .
指派问题与匈牙利算法
当人数m小于工作数n时，加上n－m个人，例如
7 0 C ′＝ 8 4
0 19 2 8 17 0 7 11 0 0 10 2
0 9 2 8 7 0 7 1 0 0 0 2
1 1 最优解： 最优解： X＝ 1 1
即甲安排做第二项工作、乙做第三项、丙做第四项、丁做第三项。 总分为： ＝ ＋ ＋ ＋ ＝ 总分为：Z＝92＋95＋90＋80＝357
§5.5 指派问题 Assignment Problem
Ch5 Integer Programming
2011年5月9日星期一 Page 6 of 12
用匈牙利法求解：
10 3 22 0 8 17 C ′＝ 13 12 16 9 5 15 7 0 C ′＝ 8 4
5 0 5 7
则 与
′ m w = ∑∑cij xij in
i j
m z = ∑∑cij xij ax
i j
的最优解相同。
§5.5 指派问题 Assignment Problem
Ch5 Integer Programming
2011年5月9日星期一 Page 5 of 12
【例】某人事部门拟招聘4人任职4项工作，对他们综合考评的 例 得分如下表（满分100分），如何安排工作使总分最多。
2011年5月9日星期一 Page 4 of 12
求最大值的指派问题 匈牙利法的条件是：模型求最小值、效率cij≥0 设C=(cij)m×m 对应的模型是求最大值 将其变换为求最小值 令
匈牙利算法示例
0 0 0 1 1 0 0 0
15
3 ◎ 2 2
3 ◎ Ø 5 1 ◎ 4 4 6 ◎ Ø 4
得到4个独 立零元素， 所以最优解 矩阵为：
练习：
费 工作 用 人员
A
7
B
5
C
9
D
8
E
11
甲
乙
丙 丁 戊
9
8 7 4
12
5 3 6
7
4 6 7
11
6 9 5
0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2
4 2
0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0
Ø 0 0 13 7 ◎ 6 0 6 9 ◎ ◎ 0 5 3 2 ◎ Ø 0 0 1 0 Ø
0 0 1 0
0 0 1 1 0 0 0 0 0 0 1 0
例二、 有一份中文说明书，需译成英、日、德、俄四种 文字，分别记作A、B、C、D。现有甲、乙、丙、丁四 人，他们将中文说明书译成不同语种的说明书所需时 间如下表所示，问如何分派任务，可使总时间最少？
任务
人员
例一：
任务
人员
A 2
10 9 7
B 15
4 14 8
C 13
14 16 11
D 4
15 13 9
甲
乙 丙 丁
2 10 9 7
15 13 4 4 14 15 14 16 13 8 11 9
2 4
9
7
0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2
2 2 4 4 ◎ 0
二分图匹配(匈牙利算法)
KM算法
对于任意的G和M,可行顶标都是存在的: l(x) = maxw(x,y) l(y) = 0 欲求完全二分图的最佳匹配,只要用匈牙利算法求 其相等子图的完备匹配;问题是当标号之后的Gl无 完备匹配时怎么办?1957年(居然比匈牙利算法 早???),Kuhn和Munkras给出了一个解决该问 题的有效算法,用逐次修改可行顶标l(v)的办法使对 应的相等子图之最大匹配逐次增广,最后出现完备 匹配.
例题3 打猎 猎人要在n*n的格子里打鸟,他可以在某一行 中打一枪,这样此行中的所有鸟都被打掉, 也可以在某一列中打,这样此列中的所有鸟 都打掉.问至少打几枪,才能打光所有的鸟? 建图:二分图的X部为每一行,Y部为每一列, 如果(i,j)有一只鸟,那么连接X部的i与Y部的j. 该二分图的最大匹配数则是最少要打的枪数.
1 2 3 4 5
1 2 5 3 4
1
2
3
4
由于每条边表示一个空地,有冲 突的空地之间必有公共顶点,所 以问题转化为二部图的最大匹配 问题.
1 2Leabharlann 34例题1 Place the Robots(ZOJ) 小结
比较前面的两个模型:模型一过于简单,没有给问 题的求解带来任何便利;模型二则充分抓住了问题的内 在联系,巧妙地建立了二部图模型.为什么会产生这种 截然不同的结果呢?其一是由于对问题分析的角度不同: 模型一以空地为点,模型二以空地为边;其二是由于对 原型中要素的选取有差异:模型一对要素的选取不充分, 模型二则保留了原型中"棋盘"这个重要的性质.由此 可见,对要素的选取,是图论建模中至关重要的一步.
例题4 最小路径覆盖 一个不含圈的有向图G中,G的一个路径覆盖 是一个其结点不相交的路径集合P,图中的每 一个结点仅包含于P中的某一条路径.路径可 以从任意结点开始和结束,且长度也为任意 值,包括0.请你求任意一个不含圈的有向图 G的最小路径覆盖数. 理清一个关系:最小路径覆盖数=G的定点 数-最小路径覆盖中的边数
匈牙利算法详解
大意：已知两个图和两个图中的点和边的连接情况，求两个图中最多能连接的边的数目。
（每个点最多只能连接一条边）分析：算法总体可以采用类似于探索的方法，例如下面的这个图。
CADBE如这个有向图，共有5个结点A、B、C、D、E，A、B作为第一张图，C、D、E作为第二张图。
第一次DFS时先看A连接的点（顺序查找）是否已经有爹了，发现没有，那么爹变成了A，同时A的匹配找到了。
再找B的匹配，发现C已经有爹了即A，那么就试探A的下一个连接点发现没有爹且能与B相连，那么B的匹配也找到了，依次类推直到推到最后。
代码：function dfs(x:longint):boolean;vari:longint;beginif use[x] then exit(false);{如果出现某个点访问过返回false。
}use[x]:=true;{同时标记为已访问过。
}for i:=1 to m dobeginif (b[x,i]) and ((link[i]=0) or (dfs(link[i]))) then{如果要连的点还没爹可以连，或者是它的爹的所连的点还有剩余就可以继续（前提是必须可以相连）。
}beginlink[i]:=x;{修改爹。
}exit(true);end;end;exit(false);end;procedure XYL;vari:longint;beginfor i:=1 to n do{先进行查找。
}beginfillchar(use,sizeof(use),false);{初始化每个点都未访问过以便遍历图。
}if dfs(i) then inc(ans);{返回true说明可以匹配。
}end;writeln(ans);end;。
匈牙利算法（二分图）
匈⽛利算法（⼆分图）---------------------------------------------------------------------题材⼤多来⾃⽹络，本篇由神犇整理基本概念—⼆分图⼆分图：是图论中的⼀种特殊模型。
若能将⽆向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为⼀个为⼆分图。
匹配：⼀个匹配即⼀个包含若⼲条边的集合，且其中任意两条边没有公共端点。
如下图，图3的红边即为图2的⼀个匹配。
1 最⼤匹配在G的⼀个⼦图M中，M的边集中的任意两条边都不依附于同⼀个顶点，则称M是⼀个匹配。
选择这样的边数最⼤的⼦集称为图的最⼤匹配问题,最⼤匹配的边数称为最⼤匹配数.如果⼀个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
如果在左右两边加上源汇点后，图G等价于⼀个⽹络流，最⼤匹配问题可以转为最⼤流的问题。
解决此问的匈⽛利算法的本质就是寻找最⼤流的增⼴路径。
上图中的最⼤匹配如下图红边所⽰：2 最优匹配最优匹配⼜称为带权最⼤匹配，是指在带有权值边的⼆分图中，求⼀个匹配使得匹配边上的权值和最⼤。
⼀般X和Y集合顶点个数相同，最优匹配也是⼀个完备匹配，即每个顶点都被匹配。
如果个数不相等，可以通过补点加0边实现转化。
⼀般使⽤KM算法解决该问题。
3 最⼩覆盖⼆分图的最⼩覆盖分为最⼩顶点覆盖和最⼩路径覆盖：①最⼩顶点覆盖是指最少的顶点数使得⼆分图G中的每条边都⾄少与其中⼀个点相关联，⼆分图的最⼩顶点覆盖数=⼆分图的最⼤匹配数；②最⼩路径覆盖也称为最⼩边覆盖，是指⽤尽量少的不相交简单路径覆盖⼆分图中的所有顶点。
⼆分图的最⼩路径覆盖数=|V|-⼆分图的最⼤匹配数；4 最⼤独⽴集最⼤独⽴集是指寻找⼀个点集，使得其中任意两点在图中⽆对应边。
对于⼀般图来说，最⼤独⽴集是⼀个NP完全问题，对于⼆分图来说最⼤独⽴集=|V|-⼆分图的最⼤匹配数。
匈牙利算法示例ppt
0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0
解矩阵得到2个最优指派方案；（1）甲-B，乙-C， 丙--E，丁-D,戊-A；（2）甲-B，乙-D，丙-E,丁-C， 戊-A。所需时间为minz=7+6+9+6+4=32
3 匈牙利法的改进
实际上很多效率矩阵用上述匈牙利法进行求解时必 须经要经历第（3）和第（4），但在这些效率矩阵 中有很大部分用改进后的匈牙利法就不需要经历第 （3）和第（4）步即可求解。
12 7 9 7 9
8
9
6
6
6
7 17 12 14 9
15 14 6 6 10
4 10 7 10 9
Min
4
7
66
6
从上面可以看到列中最小个数之和为7，而行中最小个数之 和为9,。即应该先从系数矩阵的每列元素中减去该列的最小 元素。
8 0 3 1 3 0
4
2
0 0 0 0
3 10 6 8 3 3 11 7 0 0 0 0
或
4
Ø
2 7
◎
3
Ø
5
◎Ø
◎ 11
7 3
Ø ◎ Ø
1 4 3
它具有n个独立0元素，这就得到了最优解，相应的解矩阵为
0 1 0 0 0
0 1 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 0 0 1 0 0 1 0 0
或
0 0 0 0 1 0 0 0 1 0
1 0 0 0 0
1 0 0 0 0
7 ◎ 2 Ø 2
7 ◎ 2 Ø 24ຫໍສະໝຸດ Ø3 8◎
匈牙利算法 浅析 带例子
什么是二分图，什么是二分图的最大匹配，二分图的最大匹配有两种求法，第一种是最大流（我在此假设读者已有网络流的知识）；第二种就是我现在要讲的匈牙利算法。
这个算法说白了就是最大流的算法，但是它跟据二分图匹配这个问题的特点，把最大流算法做了简化，提高了效率。
匈牙利算法其实很简单，但是网上搜不到什么说得清楚的文章。
所以我决定要写一下。
最大流算法的核心问题就是找增广路径（augment path）。
匈牙利算法也不例外，它的基本模式就是：初始时最大匹配为空while 找得到增广路径do 把增广路径加入到最大匹配中去可见和最大流算法是一样的。
但是这里的增广路径就有它一定的特殊性，下面我来分析一下。
（注：匈牙利算法虽然根本上是最大流算法，但是它不需要建网络模型，所以图中不再需要源点和汇点，仅仅是一个二分图。
每条边也不需要有方向。
）图1是我给出的二分图中的一个匹配：［1，5］和［2，6］。
图2就是在这个匹配的基础上找到的一条增广路径：3->6->2->5->1->4。
我们借由它来描述一下二分图中的增广路径的性质：(1)有奇数条边。
(2)起点在二分图的左半边，终点在右半边。
(3)路径上的点一定是一个在左半边，一个在右半边，交替出现。
（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连，不要忘记哦。
）(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。
（如图1、图2所示，［1，5］和［2，6］在图1中是两对已经配好对的点；而起点3和终点4目前还没有与其它点配对。
）(6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。
（如图1、图2所示，原有的匹配是［1，5］和［2，6］，这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。
而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。
）(7)最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。
《运筹学匈牙利法》课件
总结
匈牙利算法的优缺点和适 用范围
匈牙利算法具有较高的精度和效 率，但受数据结构限制，应用对 象有一定局限性。
匈牙利算法的进一步研究 方向
运筹学在日常生活中的重 要性和应用前景
未来可继续深入探究匈牙利算法 和其他优化算法在实际问题中的 应用，完善算法理论和算法应用。
随着科技的不断发展，运筹学在 日常生活中的应用前景越来越广 泛，对提高效率和优化资源分配 具有重要意义。
的权值之和达到最大。
解决方案
匈牙利算法
匈牙利算法是解决二分图匹 配问题最经典的算法之一， 在求解最大权匹配和最小路 径覆盖问题方面都有广泛应 用。
拓展匈牙利算法
拓展匈牙利算法是一种扩展 了匈牙利算法的新算法，可 以有效解决复杂数据结构中 的匹配问题。
Байду номын сангаас
应用案例分析
将匈牙利算法应用于实际问 题的案例分析，深入了解如 何应用该算法求解实际问题， 加深理解和应用。
匈牙利法的目的和意义
匈牙利法可以帮助我们有效解决 二分图匹配问题，例如任务分配、 稳定婚姻问题等。
问题解析
1
最小路径覆盖问题
指在一个有向无环图（DAG）里选出尽
最大权匹配问题
2
可能少的路径，这些路径覆盖了DAG图 上的每个点恰好一次。
是一类用二分图描述的优化问题，给定
一个二分图，找到一个匹配使得匹配边
《运筹学匈牙利法》PPT 课件
运筹学匈牙利法是一种优化算法，用于解决二分图匹配问题。本课件将介绍 匈牙利法的背景、意义、解析以及应用案例分析。
背景介绍
运筹学在实际生活中的应用 匈牙利法的提出背景
运筹学的方法广泛应用于物流、 交通、能源、金融等领域，帮助 优化资源分配，提高效率。
匈牙利算法 ppt课件
指派问题（分配问题） (Assignment Problem)
例5 有一份中文说明书，需翻译 成英、日、德、俄四种文字，分 别记作E、J、G、R，现有甲、 乙、丙、丁四人，他们将中文说 明书翻译成英、日、德、俄四种 文字所需时间如下，问应该如何 分配工作，使所需总时间最少？
第2页
任务 E
J
98004 06365
第25页
然后划去所在的列的其他0元素， 记作Ø。
50202 23000
10 5 7 2
98004
Ø 6365
第26页
➢从只有一个0元素的列开始， 给这个0元素加圈，记
52 0 2
23000
10 5 7 2
98004
Ø 6365
第27页
然后划去所在的行的其他0元素， 记作Ø。
➢给只有一个0元素的列（或行）的0 元素加圈，记，然后划去所在的 行（或列）的其他0元素，记作Ø。
➢反复进行上述两步，直到所有的0 元素都被圈出和划掉为止。
第13页
➢若还有没有划圈的0元素，且同行 （或列）的0元素至少有二个，从剩有 0元素最少的行（或列）开始，比较这 行各0元素所在列中0元素的数目，选 择0元素少的那列的0元素加圈，然后 划掉同行同列的其他0元素，可反复进 行，直到所有的0元素都被圈出和划掉 为止。
第4页
引入0-1变量xij=1分配第i人去完 成第j 项任务，xij=0不分配第i人去完
成第j 项任务。
分配问题的数学模型：
Min Z= cijxij
s.t. xij =1 (j=1,2……n) xij =1 (i=1,2……n)
xij 0或1
(i=1,2…..n; j=1,2……n)
数学建模匈牙利算法
数学建模匈牙利算法
（实用版）
目录
一、匈牙利算法简介
二、匈牙利算法的基本原理
三、匈牙利算法的应用实例
四、匈牙利算法的优点与局限性
正文
一、匈牙利算法简介
匈牙利算法（Hungarian algorithm）是一种求解二分图最大匹配问题的经典算法，由匈牙利数学家 Mátyás Klán 首先提出。
该算法主要用于解决一些实际问题，如任务分配、资源调度等，其核心思想是尽可能地将两个顶点之间的距离缩小，从而实现图的最大匹配。
二、匈牙利算法的基本原理
1.匈牙利算法的基本思想是“贪心”，即每一步都选择当前可以得到的最佳匹配。
2.从未匹配的顶点中选择距离最小的两个顶点进行匹配，直到所有顶点都匹配完毕或者再也找不到匹配的顶点为止。
3.如果当前未匹配的顶点数量为奇数，则无法进行匹配，算法结束。
三、匈牙利算法的应用实例
1.任务分配：假设有 n 个任务和 n 个工人，每个工人完成不同任务的效率不同，匈牙利算法可以帮助我们找到最优的任务分配方案，使得总效率最大。
2.资源调度：假设有 m 个资源和 n 个任务，每个任务需要不同数量
的资源，匈牙利算法可以帮助我们找到最优的资源调度方案，使得总资源消耗最小。
四、匈牙利算法的优点与局限性
1.优点：匈牙利算法思路简单，计算效率较高，可以解决实际生活中的许多问题。
2.局限性：匈牙利算法只能解决无向图的最大匹配问题，对于有向图和带权图，需要进行相应的改进。
最大匹配之匈牙利算法模板。。
最大匹配之匈牙利算法模板。
要学习匈牙利算法先要懂得二部图的各种概念。
下面给出由o( _ )o MiYu 总结的普通性概念，这些概念很重要，一定要懂。
二分图的基本概念: ( 意思就是全部的点分成了2个集合 x, y. 每个集合中的顶点互相间没有边 ) 一个无向图 G = V, E , 假如存在两个集合X, Y, 使得X Y=V, X Y= , 并且每一条边e={x, y} 有x X,y Y, 则称G为一个二分图(bipartite graph). 常用来表示一个二分图. 若对X中任一x 及Y中任一y 恰有一边e E, 使e = {x, y}, 则称G为彻低二分图(complete bipartite graph). 二分图的性质： ( 交叉轨和增广路的概念很重要 ) 定理：无向图G为二分图的充分须要条件是，G起码有两个顶点,且其全部回路的长度均为偶数. 匹配：设G=为二分图，假如M&be;E，并且M中没有任何两边有公共端点。
M= 时称M为空匹配. 盖点: 若M是二分图的一个匹配, 将M中的边多所关联的顶点称为盖点, 其余则为未盖点. 交叉轨: 若一条路径上属于M的边和不属于M 的边交替浮现, 则称该路径为交叉轨. 增广路径: 若路径 P 是一条起始点和尽头都是未盖点的交叉轨, 那么 P 称为 M 的增广路径. 最大匹配: G的全部匹配中边数最多的匹配称为最大匹配. 性质1 : 一条关于M的增广路径的长度必为奇数, 且路上的第一条边和最后一条边都不属于M.性质2 : 对于一条关于M的增广路径 P, 将M 中属于P的边删去, 将P中不属于M 的边添加到M中,所得到的边集合计为 M P, 则 M P 比 M 多一条匹配边.性质3 : M 为 G 的一个最大匹配当且仅当不存在关于M的增广路径.hall 定理 : 对于二分图 G = ( X, Y, E ) , 存在一个匹配M, 使得 X 的全部顶点关于M饱和的充要条件是: 对 X 的任一子集A , 对A邻接的点集为P (A), 恒有 : | P[A] | = | A |其中性质 2 和性质 3 和 hall 定理的充分性证实就是匈牙利算法的基础 .. 二分图的最小顶点笼罩 ==== 最大匹配 DAG图的最小路径笼罩数 == 节点数最大匹配数二分图的最大自立集数 = 节点数最大匹配数在二分图中求最少的点，让每条边都起码和其中的一第1页共2页。
匈牙利算法
12 7 9 7 9 7 89666 6 7 17 12 14 9 7 15 14 6 6 10 6 4 10 7 10 9 4
第23页
50202 23000 0 10 5 7 2 98004 06365
第24页
➢从只有一个0元素的行开始，给 这个0元素加圈，记
50202 23000
10 5 7 2
70202 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第49页
➢从只有一个0元素的列开始，给这个0 元素加圈，记
72 0 2 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第50页
然后划去所在的行的其他0元素，记 作Ø。
72Ø 2 4 3 00Ø Ø 8 3 5 11 8 0 0 4 4 1 4 3
第11页
2 15 13 4 2 10 4 14 15 4 (cij)= 9 14 16 13 9 7 8 11 9 7
0 13 11 2
6 0 10 11
057 4
0 13 7 0 606 9
014 2 42
053 2
010 0
第12页
第二步：进行试分配，以寻找最优解。
➢从只有一个0元素的行（或列）开 始，给这个0元素加圈，记，然后 划去所在的列（或行）的其他0元 素，记作Ø。
第34页
对没有的行，打
52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
第35页
对已打行中所有含0元素的列打
52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
第36页
再对打列中含0元素的行打 52Ø 2 2 3Ø Ø 10 5 7 2 9 8 Ø 4 Ø 6365
图论课件--匈牙利算法与最优匹配算法(精选)共34页PPT
11、不为五斗米折腰。 12、芳菊开林耀，青松冠岩列。怀此 贞秀姿 ，卓为 霜下杰 。
13、归去来兮，田蜀将芜胡不归。 14、酒能祛百虑，菊为制颓龄。 15、春蚕收长丝，秋熟靡王税。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪29、勇猛、大胆和坚定的 Nhomakorabea心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
34
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8 0 3 1 4 2 0 0 3 10 6 8 11 7 0 0 0 3 1 4
3 0 3 0 3
0 0
3 0 0
8 4 0 11 0
0 3 1 3 2 0 0 0 7 3 5 0 7 0 0 0 3 1 4 3
5 0 2 0 2 3 0 0 0 10 5 7 9 8 0 0 0 6 3 6
2 0 2 4 5
5 2 ◎ 9 Ø
◎
3 10 8 6
2 Ø Ø ◎ 5 7 2 ◎ Ø 4 3 6 5 2
Ø
第三步；作最少的直线覆盖所有0元素，以确 定该系数矩阵中能找到最多的独立元素数。 （1）对没有◎的行打√ （2）在已经打√的行中所含有的0元素打√号（3） √ 在已经打√号的列中含◎元素的行打√；（4）重复 （2）（3）直到得不出打√的行列为止（5）对没有 打√的行画一横线，有打√的列画一纵线，这就覆盖 所有0元素的最少直线数。令这一直线数为l。若 l<n,说明必须再换当前的系数矩阵，才能找到n个 独立的0元素，为此转到第四步；若l=n，而m<n， 应回到（2）（4）另行试探。
再从得到系数矩阵的每行元素中减 去该行的最小元素。
根据匈牙利法第二步，很容易得到下面的矩 阵
8 4 Ø 11
◎3
◎
1 3 2 Ø Ø 7 3 5 7 ØØ 3 1 4 3
◎ ◎ 或 ◎
8 4 Ø 11
◎
◎ 3 1 3 2 ◎Ø Ø 7 3 5 ◎ 7 Ø ◎Ø
（1）；查看每行的最小元素的个数总和r和每列的最小元素 的个数总和c。并比较r和c的大小。 （2）使指派问题的系数矩阵经变换，在各行各列中都出现0元 素。当r≥c，则先从系数矩阵的每列减去该列的最小元素，再从 所得系数矩阵的每行元素中减去该行的最小元素。反之如果当 r≤c，则先从系数矩阵的每行中减去该行的最小元素，再从所得 系数矩阵的每行元素中减去该列的最小元素。其他步奏同匈牙利 法。
bij
12 8 (cij ) 7 15 4
7 9 17 14 10
9 7 9 6 6 6 12 14 9 6 6 10 7 10 9
5 0 2 0 2 3 0 0 0 10 5 7 9 8 0 0 0 6 3 6
2 0 2 4 5
由解矩阵得到2个最优指派方案；（1）甲-B， 乙-D，丙-E，丁-C，戊-A；(2)甲-B，乙-C，丙E，丁-C，戊-A。所需总时间 Minz=7+6+9+6+4=32
4 结论
• a 改进后的匈牙利法比原来的匈牙利法大大 减少了计算量，并节省了一些很累赘的步 骤，在实际工作中可以为决策者与决策团 队节约宝贵的时间以及信息的时效性。 • b 2种方法计算结果完全一致，说明改进的 匈牙利法可以达到与原匈牙利法一样的效 果。 • c即使遇上了少数改进的匈牙利法无法改进 的系数矩阵时，也可按原匈牙利法的步骤 进行解析，不影响结果的正确性。
解矩阵得到2个最优指派方案；（1）甲-B，乙-C， 丙--E，丁-D,戊-A；（2）甲-B，乙-D，丙-E,丁-C， 戊-A。所需时间为minz=7+6+9+6+4=32
3 匈牙利法的改进
实际上很多效率矩阵用上述匈牙利法进行求解时必 须经要经历第（3）和第（4），但在这些效率矩阵 中有很大部分用改进后的匈牙利法就不需要经历第 （3）和第（4）步即可求解。
要求每人做一项工作，约束条件为
x
j 1
n
ij
1
(i 1, 2, , n)
要求每项工作只能安排一人，约束条件为
x
i 1
n
ij
1
( j 1, 2, , n)
变量约束为
xij 0或1
(i, j 1, 2,3, 4)
下表所示效率矩阵的指派问题
时间 任务 人员
A
12 8 7
上面矩阵有5个独立0元素，这就得到相应的最优解。
0 0 0 0 1
1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0
或
0 0 0 0 1
1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0
11
7 x12 9 x13 7 x14 9 x15 8 x21 9 x22
6 x23 6 x24 6 x25 7 x31 17 x32 12 x33 14 x34 9 x35 15 x41 14 x42 6 x43 6 x44 10 x45 4 x51 10 x 52 7 x53 10 x54 9 x55
3 1 4 3
它具有n个独立0元素，这就得到了最优解，相应的解矩阵为
0 0 0 0 1
1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0
或
0 0 0 0 1
1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0
第二步：进行试指派，以寻求最优解。 在(bij)中找尽可能多的独立0元素，若能找出n个 独立0元素，就以这n个独立0元素对应解矩阵(xij)中的 元素为1，其余为0，这就得到最优解。找独立0元素， 常用的步骤为： (1)从只有一个0元素的行(列)开始，给这个0元素 加圈，记作◎ 。然后划去◎ 所在列(行)的其它0元素， 记作Ø ；这表示这列所代表的任务已指派完，不必再 考虑别人了。 (2)给只有一个0元素的列(行)中的0元素加圈，记 作◎；然后划去◎ 所在行的0元素，记作Ø ． (3)反复进行(1)，(2)两步，直到尽可能多的0元素 都被圈出和划掉为止。
12 7 9 7 9 8 9 6 6 6 7 17 12 14 9 15 14 6 6 10 4 10 7 10 9
Min 4 7 6 6 6
从上面可以看到列中最小个数之和为7，而行中最小个数之 和为9,。即应该先从系数矩阵的每列元素中减去该列的最小 元素。
B
7 9 17
C
9 6 12
D
7 6 14
E
9 6 9
甲 乙 丙
丁
戊
15
414ຫໍສະໝຸດ 10676
10
10
9
（二）、匈牙利法的解题步骤：
第一步：变换指派问题的系数矩阵（cij）为 (bij)，使在(bij)的各行各列中都出现0元素，即 (1) 从（cij）的每行元素都减去该行的最小 元素； (2) 再从所得新系数矩阵的每列元素中减去 该列的最小元素。
匈牙利算的优化
例
指派问题及其解法
有甲、乙、丙、丁、戊五位工人被指派去 完成A、B 、 C 、 D 、 E五项任务，每个 人完成任务所需的工时各不相同，见下表。 求应如何指派人员才能使得所用工时最少？
解
1, xij 0，
分配第i个人做j工作时 不分配第i个人做j工作时
目标函数为
12 x
7 ◎ 2 Ø 2 4 3 ◎ Ø Ø Ø 8 3 5 ◎ 11 8 Ø ◎ 4 ◎ 4 1 4 3
或
7 ◎ 2 Ø 2 4 3 Ø◎ Ø Ø 8 3 5 ◎ 11 8 ◎ Ø 4 4 1 4 3 ◎
0 5 ◎ 2 2 3 0 Ø 0 10 5 ◎ 9 8 ◎ 0 Ø 6 3 0 ×
0 Ø 2 0 0 Ø◎
√
7 2 √ -2 0 Ø 4 6 5 -2 √
+2
第四步；在没有被直线覆盖的部分中找出 最小元素。然后在行打√行每个元素减去这 一最小元素，而在打√列的每个元素都加上 这一最小元素，以保证原来0元素不变。这 样得到新系数矩阵。若得到n个独立的0元素， 则已得到最优解，否则回到第3）。