2011 学年第二学期期末考试试卷(A卷) - 华中师范大学数学与统计学
统计学复习试题与答案(1) 2

泉州师院2010—2011学年度第二学期本科2008级《统计学》期末复习试卷A一、判断题(对的打“√”;错的打“×”,并在原题上改正。
每小题2分,共10分)1.众数是总体中出现最多的次数。
( )2.相关系数为零,说明两现象之间毫无关系。
( )3.方差分析是为了推断多个总体的方差是否相等而进行的假设检验。
( )4.对总体参数提出某种假设,然后利用样本信息判断假设是否成立的过程称为参数估计。
( )5.统计表的总标题位于表的上端,统计图的总标题也是位于图的上端( )二、单项选择题 (每小题1分,共10分)1.某森林公园的一项研究试图确定哪些因素有利于成年松树长到60英尺以上的高度。
经估计,森林公园长着25000棵成年松树,该研究需要从中随机抽取250棵成年松树并丈量它们的高度后进行分析。
该研究的总体是( B )A. 250棵成年松树B.公园里25000棵成年松树C.所有高于60英尺的成年松树D.森林公园中所有年龄的松树2.从均值为100、标准差为10的总体中,抽出一个50 n 的简单随机样本,样本均值的数学期望和方差分别为( A )A. 100和2B. 100和0.2C. 10和1.4D. 10和23.若两个变量的平均水平接近,标准差越大的变量,其( B )A .标准差代表性越大B .离散程度越大C .稳定性越高D .分布偏斜程度越严重4.某电视台就“你最喜欢的电视节目是哪个”随机询问了200名观众,为了度量调查数据的集中趋势,需要运用的指标是( D )A .算术平均数B .几何平均数C .中位数D .众数5.将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本,这种抽样方式称为( B )A.简单随机抽样B.分层抽样C.整群抽样D.系统抽样6.对总体均值进行区间估计时,其他条件不变,置信度1-α 越小,则( D )A .抽样推断的准确度越低B .抽样推断的把握程度越高C .抽样推断的可靠程度越大D .允许误差范围越小7.点估计的缺点是( C )A.不能给出总体参数的准确估计B.不能给出总体参数的有效估计C.不能给出点估计值与总体参数真实值接近程度的度量D.不能给出总体参数的准确区间8.假设检验中,拒绝域的大小与我们事先选定的( D )A.统计量有一定关系 B.临界值有一定关系C.置信水平有一定关系 D.显著性水平有一定关系9.假设检验是对未知总体某个特征提出某种假设,而验证假设是否成立的资料是(A )A.样本资料 B.总体全部资料C. 重点资料D.典型资料10.下面现象间的关系属于相关关系的是(C )A.圆的周长和它的半径之间的关系B.价格不变条件下,商品销售额与销售量之间的关系C.家庭收入愈多,其消费支出也有增长的趋势D.正方形面积和它的边长之间的关系三、多项选择题(每小题2分,共10分)1.“统计”一词有三种理解()A. 统计工作B. 统计资料C. 统计信息D. 统计科学2.根据某样本资料得居民平均收入(万元)与某种产品销售量(台)之间的回归方程为xy6820ˆ+=,这意味着()A.居民平均收入与某种产品销售量之间是负相关B.居民平均收入与某种产品销售量之间是正相关C.居民平均收入为1万元时,某种产品的销售量平均为826台D.居民平均收入每增加1万元,某种产品销售量平均增加6台E.居民平均收入每增加1万元,某种产品销售量平均减少6台3.在参数估计中,评价估计量好坏的标准有()A. 无偏性B. 有效性C. 相合性D. 一致性4.假设检验中所犯错误有两种类型()A. 取真错误B. 弃真错误C. 取伪错误D. 弃伪错误5.样本单位数取决于下列因素()A. 被研究总体的标志变异程度B. 抽样极限误差C. 抽样调查组织方式和抽样方法D. 研究的代价四、填空题(每空1分,共10分)1.在实际试验中,许多不能控制的偶然因素引起试验结果数值的差异,称为______误差。
(完整)高等数理统计2011

南昌大学研究生2010~2011学年第 2 学期期末考试试卷试卷编号: ( A )卷课程名称: 高等数理统计 适用专业: 数学 姓名: 学号: 专业: 学院: 考试日期: 2011年6月19日 考试占用时间: 150分钟 考试形式(开卷或闭卷):题号 一 二 三 四 五 六七八九十总分 累分人 签名题分 1515202525100 得分考生注意事项:1、本试卷共 页,请查看试卷中是否有缺页或破损。
如有立即举手报告以便更换。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
一、证明题: (15分)得分 评阅人设1(0,1):X N ,2(0,4):X N ,且1X 与2X 独立,求112=+Y X X 与212=-Y X X 的联合分布。
二、计算题:(15分)得分 评阅人设总体X 有密度函数201()0<<⎧=⎨⎩其它x x p x ,从该总体随机抽取一个容量为4的样本,计算概率(3)(0.5)>P X 。
三、综合题:(20分)得分 评阅人(1) 检查Poisson 布族的完备性;(2) 判断分布族{(1),0,1,2,;0}θθθθ=-=>L x p x 是否为指数族;四、应用题:(25分)得分 评阅人设1,,L n X X 为独立同分布变量,01θ<<,11Pr(1)2θ-=-=X , 11Pr(0)2==X , 1Pr(1)2θ==X , (1) 求θ的1ˆθMLE 并问1ˆθ是否是无偏的; (2) 求θ的矩估计2ˆθ; (3) 计算θ的无偏估计的方差的C-R 下界。
五、综合题:(25分)得分 评阅人设1X ,2X 独立同分布,其共同的密度函数为:23(;)3, 0,0θθθθ=<<>p x x x(1) 证明1122()3=+T x x 和2127max(,)6=T x x 都是θ的无偏估计;(2) 计算1T 和2T 的均方误差并进行比较; (3) 证明:在均方误差意义下,在形如12max(,)=c T c x x 的估计中,87T 最优。
11学年第二学期大学数学2试卷(A卷)-参考答案
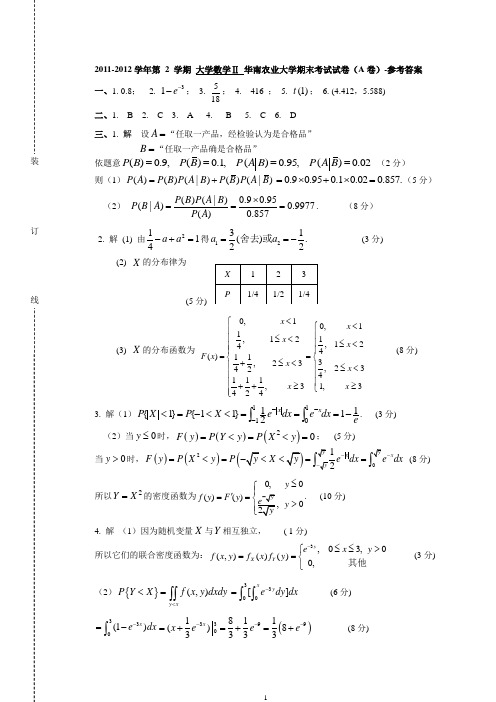
2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3. 518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分) 则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分)(2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分) 2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为 (5分) (3) X 的分布函数为 0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分)3. 解(1)111011{1}{11}12x x P X P X e dx e dx e ---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(20x x F y P X y P X dx dx --=<=<== (8分)所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分)4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他(3分)(2){}(,)y x P Y X f x y dxdy <<=⎰⎰3300[]x y edy dx -=⎰⎰ (6分) 330(1)x e dx -=-⎰3390181()333xx e e --=+=+()9183e -=+ (8分)(3)解:由密度函数可知~(0,3),~(3)X U Y E (10分) 所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+= (14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分) 依题意,取统计量:222(1)~(1)n S n χχσ-=-,15n =. (3分) 查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分) 计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分) 因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异. (8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分) 因此所求回归直线方程为 ˆ24.7725.86y x =-+ (8分)。
统计学期末考试试卷A卷2011.11答案

一、选择题(每题2分,共2*5=10分)1、从含有N个元素的总体中,抽取n个元素作为样本,使得总体中的每一个元素都有相同的机会(概率)被抽中,这样的抽样方式称为( A )A、简单随机抽样B、分层抽样C、系统抽样D、整群抽样2、对平均值相差较大的两个总体比较其离散程度时,应采用(D )指标A、全距B、平均差C、标准差D、变异系数3、若随机事件A,B互不相容,则P(A∪B) = ( A )A、P(A)+P(B)B、P(A)+P(B)−P(A)P(B)C、P(A)P(B)D、P(A) −P(B)4、下面关于95%的置信度说法正确的是(C )A、总体参数落在一个特定的样本所构造的区间内的概率为95%B、总体参数落在一个特定的样本所构造的区间内的概率为5%C、对总体均值估计时,进行100次抽样(样本容量为n),由样本均值加减估计的允许误差所构造的100个置信区间中,平均有95个包含总体参数的真实值D、对总体均值估计时,进行100次抽样(样本容量为n),由样本均值加减估计的允许误差所构造的100个置信区间中,平均有5个包含总体参数的真实值5、假设检验中,分别用α,β表示犯第I类错误和第II类错误的概率,则当样本容量n一定时,下列说法中正确的是( A )A、α是指原假设H0为真,但却拒绝了原假设的概率B、α是指原假设H0为假,但却接受了原假设的概率C、α减小时β也减小D、α增大时β也增大二、填空题(每题3分,共3*10=30分)1、在统计学的研究中,感兴趣的研究对象全体称为总体;每个组成对象称为个体。
2、有10个人的年龄资料:10,20,15,20,25,30,15,20,30,25岁。
由该资料确定的中位数为20 ,众数为20 ,极差为20 。
3、射手独立地射击5次,每次命中目标的概率均为0.6。
则刚好有3次命中的概率()3P X == 0.3456 。
4、设连续型随机变量X 在有限区间(a ,b )内取值,且X 服从均匀分布,其概率密度函数为1()0,a x b f x b a ⎧≤≤⎪=-⎨⎪⎩,其他,则X 的期望值为 2a b + ,方差为 2()12b a - 。
统计学期末考试卷试题库题集及标准答案.doc

统计学期末考试卷试题库题集及标准答案.doc统计学期末考试题库及答案一、填空题1.标志是说明特征的;指标是说明数量特征的。
2.标志可以分为标志和标志。
3.变量按变量值的表现形式不同可分为变量和变量。
4.统计学是研究如何、、显示、统计资料的方法论性质的科学。
5.配第在他的代表作《》中;用数字来描述;用数字、重量和尺度来计量;为统计学的创立奠定了方法论基础。
二、判断题1.企业拥有的设备台数是连续型变量。
()2.学生年龄是离散型变量。
()3.学习成绩是数量标志。
()4.政治算术学派的创始人是比利时的科学家凯特勒;他把概率论正式引进统计学。
()5.指标是说明总体的数量特征的。
()6.对有限总体只能进行全面调查。
()7.总体随着研究目的的改变而变化。
()8.要了解某企业职工的文化水平情况;总体单位是该企业的每一位职工。
()9.数量指标数值大小与总体的范围大小有直接关系。
()10.某班平均成绩是质量指标。
()三、单项选择题1. 考察全国的工业企业的情况时;以下标志中属于数量标志的是()。
A. 产业分类B.劳动生产率C.所有制形式D.企业名称2. 要考察全国居民的人均住房面积;其统计总体是()。
A. 全国所有居民户B.全国的住宅C.各省市自治区D.某一居民户3. 若要了解全国石油企业采油设备情况;则总体单位是()。
A. 全国所有油田B.每一个油田C.每一台采油设备D.所有采油设备4. 关于指标下列说法正确的是()。
A. 指标是说明总体单位数量特征的B.指标都是用数字表示的C. 数量指标用数字表示;质量指标用文字表示D.指标都是用文字表示的5. 政治算术学派的代表人物是()。
A. 英国人威廉·配第B.德国人康令C. 德国人阿亨瓦尔D. 比利时人凯特勒6. 关于总体下列说法正确的是 ( ) 。
A. 总体中的单位数都是有限的B. 对于无限总体只能进行全面调查C. 对于有限总体只能进行全面调查D. 对于无限总体只能进行非全面调查7. 关于总体和总体单位下列说法不正确的是()。
华中师范大学统计学期末考试高分题库全集含答案

155233--华中师范大学统计学期末备考题库155233奥鹏期末考试题库合集单选题:(1)编制单位成本指数时,同度量因素一般应采用()。
A.报告期产量B.基期产量C.基期成本价D.报告期成本价正确答案:A(2)中位数是( )。
A.数量中出现次数最多的变量值B.顺序大小排列位置在正中间的变量值C.抽样时中选的变量值D.用权数计算出的变量值正确答案:B(3)标准差越小,则反映变量值( )。
A.越分散、平均数代表性越差B.越集中、平均数代表性越差C.越集中、平均数代表性越好D.越分散、平均数代表性越好正确答案:C(4)一组样本数据为3,3,1,5,13,12,11,9,7。
这组数据的中位数是()A.3B.13C.7.1D.7正确答案:D(5)平均增长速度是()A.长环增长速度的算术平均数B.总增长速度的算术平均数C.平均发展速度减去百分之百D.环比发展速度的序时平均数正确答案:C(6)用简单随机重复抽样方法选取样本的时候,如果要使抽样平均误差降低50%,则样本容量需要扩大到原来的( )。
A.2倍B.3倍C.4倍D.5倍正确答案:C(7)当变量x值减少时,变量y值增加,则x与y之间存在着( )。
A.直线相关关系B.正相关关系C.曲线相关关系D.负相关关系正确答案:D(8)能够测定变量之间相关系密切程度的主要方法是( )。
A.相关表B.相关图C.相关系数D.定性分析正确答案:C(9)统计是( )的科学。
A.社会B.自然C.综合D.方法论正确答案:D(10)“统计”一词的三种涵义是( )。
A.统计调查、统计整理、统计分析B.统计工作、统计资料、统计科学C.统计信息、统计咨询、统计监督D.统计理论、统计方法、统计技能正确答案:B(11)区别重点调查和典型调查的标志是( )。
A.调查单位数目不同B.收集资料方法不同C.确定调查单位标准不同D.确定调查单位目的不同正确答案:C(12)研究某高中的学生高考情况,其统计总体为( )。
(完整版)微分几何期末考试

6、曲面的第一基本形式 ds 2
du2 dv2 (u 2 v2 C)2
,则 122
__________________________
7、曲面
r
(u, v, u 2
v2
) 在 P(1,1, 2)
处的主方向为________________________________
得分 评阅人
二、判断题:(共 5 题,每题 3 分,在括号里填写正确或错误)
1、(10
分)已知曲面
S:
r
r (u,
v)
的高斯曲率和平均曲率分别为
K
和
H,则曲面
S
的三
个基本形式满足:
KI-2HⅡ+Ⅲ=0 .
第 2 页(共 3 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
C:
r
(t,
sin
t,(t
))
的主法线与
yOz
平面平行,是确定 (t
)
.
2、 (8 分)找出双曲面 z axy 上的曲率线.
第 1 页(共 3 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
2011数二真题及解析

2011数二真题及解析题目一题目描述已知函数f(f)=f2+ff+f在区间[1,2]上为减函数,且f(1)=2,f(2)=1,求函数f(f)的解析式。
解析由题目已知,函数f(f)=f2+ff+f在区间[1,2]上为减函数,即在该区间上f′(f)<0。
又根据函数的导数的性质,有f′(f)=2f+f。
因此,要使f(f)在区间[1,2]上为减函数,必须满足f′(f)< 0,即2f+f<0。
又知道f(1)=2,即将f=1代入f(f)的解析式,得到1+ f+f=2,即f+f=1。
再将f(2)=1,即将f=2代入f(f)的解析式,得到4+2f+f=1,即2f+f=−3。
将f+f=1和2f+f=−3联立,可以求解得到f=−2和f=3。
因此,函数f(f)的解析式为f(f)=f2−2f+3。
题目二题目描述设随机变量f的概率密度函数为$ f(x) = \begin{cases} kx^2, & \text{0<x<1} \\ 0, & \text{其他} \end{cases} $求常数f的值。
解析根据随机变量的概率密度函数的性质,概率密度函数f(f)需要满足以下两个条件:1.$f(x) \\geq 0$,即在定义区间内,概率密度函数的取值不能为负。
2.$\\int_{-\\infty}^{\\infty} f(x) dx = 1$,即概率密度函数的积分等于1。
由题目已知条件可知,在定义区间0<f<1内,$f(x)\\geq 0$,因此可以得到$kx^2 \\geq 0$,即$k \\geq 0$。
又根据第二个条件,计算概率密度函数的积分:$\\int_{-\\infty}^{\\infty} f(x) dx = \\int_{0}^{1} kx^2 dx = \\frac{k}{3}x^3 \\Bigg|_{0}^{1} = \\frac{k}{3}$根据第二个条件可知$\\frac{k}{3}=1$,因此f=3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
g
3
du 2 d 2u1 du j du i dt 1 ij dt dt 2 dt dt ds
g.
得分
评阅人
1. 三、证明题: (共 1 题, 15 分)
9.设两曲面沿交线成定角,证明:如果交线是一张曲面的曲率线,则它也是另一张曲面的曲率线. 证明 交线成定角即法向量成定角,也就是 n1 n2 c .
解: 直接计算得:
r
dr dt du i dt du k dt ri rk , dt ds dt ds dt ds
2 2
j i d 2u k du k d 2t du j du i dt k du du dt 2 ij r hij n rk rk . dt dt ds dt ds 2 dt dt ds dt
k 答: ij
专业:
1 kl gil g jl gij g ( j i l )。 2 u u u
: 院(系)
得分
评阅人
二、计算题: (共 3 题,每题 15 分,共 45 分)
6.设曲线的参数表示为 r (a cos t , a sin t , bt ) 。计算它的曲率、挠率和三个基本向量。 解: r {a sin t , a cos t , b} ,
A
Kd K ( A)
A
( A)
a2
其中 ( A) 是 A 的面积,所以 ,
( A) 为 2 a
2
4 a
,球面的面积是
2
第 2 页(共 2 页)
{cos cos ,cos sin ,sin }
第 1 页(共 3 页)
r {R cos cos, R cos sin ,0}
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
j i du1 d 2u 2 2 du du dt r r ij r1 r2 dt dt 2 dt dt ds 3 j i du 2 d 2 u 1 1 du du dt ij r1 r2 dt dt 2 dt dt ds 3
两边对弧长求导得 n1 n2 n1 n2 0 . 由于交线是第一张曲面的曲率线,由罗德里格定理, n1 r , 所以 n1 n2 0 ,于是 n1 n2 0 ,这说明 n1 n2 . 另一方面, n2 n2 ,所以 n2 / / n1 n2 / / r ,
再由罗德里格定理可知交线是第二张曲面的曲率线.
得分
评阅人
四、应用题: (共 1 题, 15 分)
10.应用高斯-波涅定理计算半径为 a 的球面的面积。 解:设赤道圆为 C,则它是测地线,在其上 kg 0
球面的高斯曲率是
K
1 a2
设上半球面为 A,由高斯-波涅定理有 因 K 为常数,
Kd 2 ,
hij
所以
du k dt du j du i dt ds dt dt
dt rk n. ds
3
2
j i du1 d 2u 2 2 du du dt r g r n ij dt dt 2 dt dt ds
|
1 {b sin t , b cos t , a} a b2
2
7.计算球面 r {R cos cos , R cos sin , R sin } 的第一基本形式、第二基本形式、高斯曲率、平均 曲率。 解: r {R cos sin , R cos sin ,0}
r {R sin sin , R sin cos,0}
r {R cos cos , R cos sin , R sin }
L r n R cos2 , M r n 0, N r n R
年级:
i , j 1
g du du , II L du du
i j i ij i , j 1 ij
2
2
j
,其中 I 正定。如果 gij , Lij 满足高斯方程
和科达齐方程, 则存在一张曲面 S 以 I 为第一基本形式, II 为第二基本形式, 以 并且这样的两张曲面通 过运动可以重合。 3. 叙述曲面映射是等距的一个等价条件。 答:保持内积。 4. 叙述高斯波涅公式。 答:高斯曲率的积分、测地曲率在边界上的积分与边界的外角之和等于 2π 。 5. 叙述克氏符号的定义。
| r r | a k 3 2 2 | r | a b (r , r , r ) b 2 2 2 | r r | a b r 1 2 2 {a sin t , a cos t , b} | r | a b
期末考试试卷(A 卷)答案
课程名称 微分几何 课程编号 83410019 任课教师 周振荣、程亮、陈永发 题型 分值 得分 叙述 25 计算 45 证明 15 应用 15 总分 100
学生姓名:
学号:
得分
评阅人
一、叙述题: (共 5 题,每题 5 分,共 25 分)
1. 叙述高斯奇妙定理。 答: 高斯曲率是内蕴量。 2. 叙述曲面基本定理。 答:给定两个二次型 I
r {R sin cos , R sin sin , R cos}
E r 2 R2 cos2 , F r r 0, G r 2 R2
I R2 cos2 d 2 R2d 2
n
r r EG F 2
II ( R cos2 d 2 Rd 2 )
K H LN M 2 1 2 2 EG F R LG 2MF NE 1 2 2( EG F ) R
1 2 8.设曲面 S : r r (u1 , u 2 ) 上的曲线 C : r (t ) r u (t ), u (t ) ,求测地挠率.
r {a cos t , a sin t ,0}
r {a sin t , a cos t , 0}
r r {ab sin t , ab cos t , a2} (r, r, r) a2b ,| r |2 a 2 b2
华中师范大学 2010 –2011 学年第二学期
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
