哈工大材料力学大作业--matlab编程
MATLAB编程练习(含答案很好的)

001双峰曲线图:z=peaks(40);mesh(z);surf(z)002解方程:A=[3,4,-2;6,2,-3;45,5,4];>> B=[14;4;23];>> root=inv(A)*B003傅里叶变换load mtlb ;subplot(2,1,1);plot(mtlb);>> title('原始语音信息');>> y=fft(mtlb);>> subplot(2,1,2);>> yy=abs(y);>> plot(yy);>> title('傅里叶变换')004输入函数:a=input('How many apples\n','s')005输出函数a=[1 2 3 4 ;5 6 7 8;12 23 34 45;34 435 23 34]a =1 2 3 45 6 7 812 23 34 4534 435 23 34disp(a)a =1 2 3 45 6 7 812 23 34 4534 435 23 34b=input('how many people\n' ,'s')how many peopletwo peopleb =two people>> disp(b)two people>>006求一元二次方程的根a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/(2*a)x1 =-1.0000 + 1.4142i>> x2=(-b-d)/(2*a)x2 =-1.0000 - 1.4142i007求矩阵的相乘、转置、存盘、读入数据A=[1 3 5 ;2 4 6;-1 0 -2;-3 0 0];>> B=[-1 3;-2 2;2 1];>> C=A*BC =3 142 20-3 -53 -9>> C=C'C =3 2 -3 314 20 -5 -9>> save mydat C>> clear>> load mydat C008编写数学计算公式:A=2.1;B=-4.5;C=6;D=3.5;E=-5;K=atan(((2*pi*A)+E/(2*pi*B*C))/D) K =1.3121009A=[1 0 -1;2 4 1;-2 0 5];>> B=[0 -1 0;2 1 3;1 1 2];>> H=2*A+BH =2 -1 -26 9 5-3 1 12>> M=A^2-3*BM =3 3 -62 13 -2-15 -3 21>> Y=A*BY =-1 -2 -29 3 145 7 10>> R=B*AR =-2 -4 -1-2 4 14-1 4 10>> E=A.*BE =0 0 04 4 3-2 0 10>> W=A\BW =0.3333 -1.3333 0.66670.2500 1.0000 0.25000.3333 -0.3333 0.6667 >> P=A/BP =-2.0000 3.0000 -5.0000-5.0000 3.0000 -4.00007.0000 -9.0000 16.0000>> Z=A.\BWarning: Divide by zero.Z =0 -Inf 01.0000 0.2500 3.0000-0.5000 Inf 0.4000>> D=A./BWarning: Divide by zero.D =Inf 0 -Inf1.0000 4.0000 0.3333-2.0000 0 2.5000010a=4.96;b=8.11;>> M=exp(a+b)/log10(a+b)M =4.2507e+005011求三角形面积:a=9.6;b=13.7;c=19.4;>> s=(a+b+c)/2;>> area=sqrt(s*(s-a)*(s-b)*(s-c))area =61.1739012逻辑运算A=[-1 0 -6 8;-9 4 0 12.3;0 0 -5.1 -2;0 -23 0 -7]; >> B=A(:,1:2)B =-1 0-9 40 00 -23>> C=A(1:2,:)C =-1.0000 0 -6.0000 8.0000 -9.0000 4.0000 0 12.3000>> D=B'D =-1 -9 0 00 4 0 -23>> A*Bans =1.0000 -184.0000-27.0000 -266.90000 46.0000 207.0000 69.0000>> C<Dans =0 0 1 01 0 0 0>> C&Dans =1 0 0 00 1 0 1>> C|Dans =1 1 1 11 1 0 1>> ~C|~Dans =0 1 1 11 0 1 0013矩阵运算练习:A=[8 9 5;36 -7 11;21 -8 5]A =8 9 536 -7 1121 -8 5>> BB =-1 3 -22 0 3-3 1 9>> RT=A*BRT =-5 29 56-83 119 6-52 68 -21>> QW=A.*BQW =-8 27 -1072 0 33-63 -8 45>> ER=A^3ER =6272 3342 294415714 -856 52608142 -1906 2390 >> BF=A.^3BF =512 729 12546656 -343 13319261 -512 125 >> A/Bans =3.13414.9634 -0.4024-1.2561 12.5244 -3.2317-1.9878 6.4512 -2.0366>> EKV=B\AEKV =10.7195 -1.2683 3.52449.4756 1.5854 3.71954.8537 -1.4878 1.3171>> KDK=[A,B]KDK =8 9 5 -1 3 -236 -7 11 2 0 321 -8 5 -3 1 9 >> ERI=[A;B]ERI =8 9 536 -7 1121 -8 5-1 3 -22 0 3-3 1 9014一般函数的调用:A=[2 34 88 390 848 939];>> S=sum(A)S =2301>> min(A)ans =2>> EE=mean(A)EE =383.5000>> QQ=std(A)QQ =419.3794>> AO=sort(A)AO =2 34 88 390 848 939 >> yr=norm(A)yr =1.3273e+003>> RT=prod(A)RT =1.8583e+012>> gradient(A)ans =32.0000 43.0000 178.0000 380.0000 274.5000 91.0000 >> max(A)ans =939>> median(A)ans =239>> diff(A)ans =32 54 302 458 91>> length(A)ans =6>> sum(A)ans =2301>> cov(A)ans =1.7588e+005>>015矩阵变换:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> tril(A)ans =34 0 08 34 034 55 2>> triu(A)ans =34 44 230 34 230 0 2>> diag(A)ans =34342norm(A)ans =94.5106>> rank(A)ans =3>> det(A)ans =-23462>> trace(A)ans =70>> null(A)ans =Empty matrix: 3-by-0>> eig(A)ans =80.158712.7671-22.9257>> poly(A)ans =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> logm(A)Warning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrixlogarithm is returned.> In funm at 153In logm at 27ans =3.1909 + 0.1314i 1.2707 + 0.1437i 0.5011 - 0.2538i0.4648 + 0.4974i 3.3955 + 0.5438i 0.1504 - 0.9608i0.2935 - 1.2769i 0.8069 - 1.3960i 3.4768 + 2.4663i>> fumn(A)Undefined command/function 'fumn'.>> inv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> cond(A)ans =8.5072>> chol(A)Error using ==> cholMatrix must be positive definite.>> lu(A)ans =34.0000 44.0000 23.00000.2353 23.6471 17.58821.0000 0.4652 -29.1816>> pinv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> svd(A)ans =94.510622.345611.1095>> expm(A)ans =1.0e+034 *2.1897 4.3968 1.93821.31542.6412 1.16431.8782 3.7712 1.6625>> sqrtm(A)ans =5.2379 + 0.2003i 3.4795 + 0.2190i 1.8946 - 0.3869i0.5241 + 0.7581i 5.1429 + 0.8288i 2.0575 - 1.4644i3.0084 - 1.9461i4.7123 - 2.1276i 2.1454 + 3.7589i >>016多项式的计算:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> P=poly(A)P =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> PPA=poly2str(P,'X')PPA =X^3 - 70 X^2 - 1107 X + 23462017多项式的运算:p=[2 6 8 3];w=[32 56 0 2];>> m=conv(p,w)m =64 304 592 548 180 16 6 >> [q,r]=deconv(w,p)q =16r =0 -40 -128 -46>> dp=polyder(w)dp =96 112 0>> [num,den]=polyder(w,p)num =80 512 724 312 -16den =4 24 68 108 100 48 9>> b=polyfit(p,w,4)Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 74b =-0.6704 9.2037 -32.2593 0 98.1333>> r=roots(p)r =-1.2119 + 1.0652i-1.2119 - 1.0652i-0.5761018求多项式的商和余p=conv([1 0 2],conv([1 4],[1 1]))p =1 5 6 10 8>> q=[1 0 1 1]q =1 0 1 1>> [w,m]=deconv(p,q)w =1 5m =0 0 5 4 3>> cq=w;cr=m;>> disp([cr,poly2str(m,'x')])5 x^2 + 4 x + 3>> disp([cq,poly2str(w,'x')])x + 5019将分式分解a=[1 5 6];b=[1];>> [r,p,k]=residue(b,a)r =-1.00001.0000p =-3.0000-2.0000k =[]020计算多项式:a=[1 2 3;4 5 6;7 8 9];>> p=[3 0 2 3];>> q=[2 3];>> x=2;>> r=roots(p)r =0.3911 + 1.0609i0.3911 - 1.0609i-0.7822>> p1=conv(p,q)p1 =6 9 4 12 9>> p2=poly(a)p2 =1.0000 -15.0000 -18.0000 -0.0000 >> p3=polyder(p)p3 =9 0 2>> p4=polyval(p,x)p4 =31021求除式和余项:[q,r]=deconv(conv([1 0 2],[1 4]),[1 1 1])022字符串的书写格式:s='student's =student>> name='mary';>> s1=[name s]s1 =marystudent>> s3=[name blanks(3);s]s3 =marystudent>>023交换两个数:clearclca=[1 2 3 4 5];b=[6 7 8 9 10];c=a;a=b;b=c;ab24If语句n=input('enter a number,n=');if n<10nend025 if 双分支结构a=input('enter a number ,a=');b=input('enter a number ,b=');if a>bmax=a;elsemax=b;endmax026三个数按照由大到小的顺序排列:A=15;B=24;C=45;if A<BT=A;A=B;B=T;elseif A<CT=A;A=C;C=T;elseif B<CT=B;B=C;C=T;endABC027建立一个收费优惠系统:price=input('please jinput the price : price=') switch fix(price/100)case[0,1]rate =0;case[2,3,4]rate =3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)028:while循环语句i=0;s=0;while i<=1212s=s+i;i=i+1;ends029,用for循环体语句:sum=0;for i=1:1.5:100;sum=sum+i;endsum030循环的嵌套s=0;for i=1:1:6;for j=1:1:8;s=s+i^j;end;end;s031continue 语句的使用:for i=100:120;if rem(i,7)~=0;continue;end;iend032x=input ('输入X的值x=')if x<1y=x^2;elseif x>1&x<2y=x^2-1;elsey=x^2-2*x+1;endy033求阶乘的累加和sum=0;temp=1;for n=1:10;temp=temp*n;sum=sum+temp;endsum034对角线元素之和sum=0;a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]; for i=1:4;sum=sum+a(i,i);endsum035用拟合点绘图A=[12 15.3 16 18 25];B=[50 80 118 125 150.8];plot(A,B)036绘制正玄曲线:x=0:0.05:4*pi;y=sin(x);plot(x,y)037绘制向量x=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18] plot(x)x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1.5 1.6 1.9 2.3]plot(x)x=0:0.2:2*piy=sin(x)plot(x,y,'m:p')038在正弦函数上加标注:t=0:0.05:2*pi;plot(t,sin(t))set(gca,'xtick',[0 1.4 3.14 56.28])xlabel('t(deg)')ylabel('magnitude(v)')title('this is a example ()\rightarrow 2\pi')text(3.14,sin(3.14),'\leftarrow this zero for\pi')039添加线条标注x=0:0.2:12;plot(x,sin(x),'-',x,1.5*cos(x),':');legend('First','Second',1)040使用hold on 函数x=0:0.2:12;plot(x,sin(x),'-');hold onplot(x,1.5*cos(x),':');041一界面多幅图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)')subplot(222);plot(x,y2);title('cos(x)')subplot(223);plot(x,y3);title('sin(2x)')subplot(224);plot(x,y4);title('cos(2x)')042染色效果图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)');fill(x,y1,'r') subplot(222);plot(x,y2);title('cos(x)');fill(x,y2,'b') subplot(223);plot(x,y3);title('sin(2x)');fill(x,y3,'k') subplot(224);plot(x,y4);title('cos(2x)');fill(x,y4,'g')043特殊坐标图clcy=[0,0.55,2.5,6.1,8.5,12.1,14.6,17,20,22,22.1] subplot(221);plot(y);title('线性坐标图');subplot(222);semilogx(y);title('x轴对数坐标图');subplot(223);semilogx(y);title('y轴对数坐标图');subplot(224);loglog(y);title('双对数坐标图')t=0:0.01:2*pi;r=2*cos(2*(t-pi/8));polar(t,r)044特殊函数绘图:fplot('cos(tan(pi*x))',[-0.4,1.4])fplot('sin(exp(pi*x))',[-0.4,1.4])045饼形图与条形图:x=[8 20 36 24 12];subplot(221);pie(x,[1 0 0 0 1]);title('饼图');subplot(222);bar(x,'group');title('垂直条形图');subplot(223);bar(x,'stack');title('累加值为纵坐标的垂直条形图'); subplot(224);barh(x,'group');title('水平条形图');046梯形图与正弦函数x=0:0.1:10;y=sin(x);subplot(121);stairs(x);subplot(122);stairs(x,y);047概率图x=randn(1,1000);y=-2:0.1:2;hist(x,y)048向量图:x=[-2+3j,3+4j,1-7j];subplot(121);compass(x);rea=[-2 3 1];imag=[3 4 -7];subplot(122);feather(rea,imag);049绘制三维曲线图:z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)x=-10:0.5:10;y=-8:0.5:8;[x,y]=meshgrid(x,y);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); subplot(221);mesh(x,y,z);title('普通一维网格曲面');subplot(222);meshc(x,y,z);title('带等高线的三维网格曲面'); subplot(223);meshz(x,y,z);title('带底座的三维网格曲面'); subplot(224);surf(x,y,z);title('充填颜色的三维网格面')050 带网格二维图x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,'r+-',x,y2,'k*:')grid onxlabel('Independent Variable x') ylabel('Dependent Variable y1&y2') text(1.5,0.5,'cos(x)')051各种统计图y=[18 5 28 17;24 12 36 14;15 6 30 9]; subplot(221);bar(y)x=[4,6,8];subplot(222);bar3(x,y)subplot(223);bar(x,y,'grouped') subplot(224);bar(x,y,'stack')052曲面图x=-2:0.4:2;y=-1:0.2:1;[x,y]=meshgrid(x,y);z=sqrt(4-x.^2/9-y.^2/4); surf(x,y,z)grid on053创建符号矩阵e=[1 3 5;2 4 6;7 9 11];m=sym(e)符号表达式的计算问题因式分解:syms xf=factor(x^3-1)s=sym('sin(a+b)'); expand(s)syms x tf=x*(x*(x-8)+6)*t; collect(f)syms xf=sin(x)^2+cos(x)^2; simplify(f)syms xs=(4*x^2+8*x+3)/(2*x+1); simplify(s)通分syms x yf=x/y-y/x;[m,n]=numden(f)嵌套重写syms xf=x^4+3*x^3-7*x^2+12; horner(f)054求极限syms x a;limit(exp(-x),x,0,'left')求导数syms xdiff(x^9+x^6)diff(x^9+x^6,4)055求不定积分与定积分syms x ys=(4-3*x^2)^2;int(s)int(x/(x+y),x)int(x^2/(x+2),x,1,3) double(ans)056函数的变换:syms x ty=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)057求解方程syms a b c xs=a*x^2+b*x+c;solve(s)syms x y zs1=2*x^2+y^2-3*z-4;s2=y+z-3;s3=x-2*y-3*z;[x,y,z]=solve(s1,s2,s3)058求微分方程:y=dsolve('Dy-(t^2+y^2)/t^2/2','t')059求级数和syms x ksymsum(k)symsum(k^2-3,0,10)symsum(x^k/k,k,1,inf)060泰勒展开式syms xs=(1-x+x^2)/(1+x+x^2);taylor(s)taylor(s,9)taylor(s,x,12)taylor(s,x,12,5)061练习syms x a;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)syms xs=x*cos(x);diff(s)diff(s,2)diff(s,12)syms xs1=x^4/(1+x^2);int(s1)s2=3*x^2-x+1int(s2,0,2)syms x y zs1=5*x+6*y+7*z-16;s2=4*x-5*y+z-7;s3=x+y+2*z-2;[x,y,z]=solve(s1,s2,s3)syms x yy=dsolve('Dy=exp(2*x-y)','x')y=dsolve('Dy=exp(2*x-y)','y(0)=0','x')n=sym('n');s=symsum(1/n^2,n,1,inf)x=sym('x');f=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);taylor(f,6)062求于矩阵相关的值a=[2 2 -1 1;4 3 -1 2;8 5 -3 4;3 3 -2 2]adet=det(a)atrace=trace(a)anorm=norm(a)acond=cond(a)arank=rank(a)eiga=eig(a)063矩阵计算A=[0.1389 0.6038 0.0153 0.9318;0.2028 0.2772 0.7468 0.4660;0.1987 0.1988 0.4451 0.4186]B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)064求根及求代数式的值P=[4 -3 2 5];x=roots(P)x=[3 3.6];F=polyval(P,x)065多项式的和差积商运算:f=[1 2 -4 3 -1]g=[1 0 1]g1=[0 0 1 0 1]f+g1f-g1conv(f,g)[q,r]=deconv(f,g)polyder(f)066各种插值运算:X=0:0.1:pi/2;Y=sin(X);interp1(X,Y,pi/4)interp1(X,Y,pi/4,'nearest')interp1(X,Y,pi/4,'spline')interp1(X,Y,pi/4,'cubic')067曲线的拟合:X=0:0.1:2*pi;Y=cos(X);[p,s]=polyfit(X,Y,4)plot(X,Y,'K*',X,polyval(p,X),'r-')068求函数的最值与0点x=2:0.1:2;[x,y]=fminbnd('x.^3-2*x+1',-1,1) [x,y]=fzero('x.^3-2*x+1',1)069求多项式的表达式、值、及图像y=[1 3 5 7 19]t=poly(y)x=-4:0.5:8yx=polyval(t,x)plot(x,yx)070数据的拟合与绘图x=0:0.1:2*pi;y=sin(x);p=polyfit(x,y,5);y1=polyval(p,x)plot(x,y,'b',x,y1,'r')071求代数式的极限:syms xf=sym('log(1+2*x)/sin(3*x)');b=limit(f,x,0)072求导数与微分syms xf=sym('x/(cos(x))^2');y1=diff(f)y2=int(f,0,1)078划分网格函数[x,y]=meshgrid(-2:0.01:2,-3:0.01:5); t=x.*exp(-x.^2-y.^2);[px,py]=gradient(t,0.05,0.1);td=sqrt(px.^2+py.^2);subplot(221)imagesc(t)subplot(222)imagesc(td)colormap('gray')079求多次多项方程组的解:syms x1 x2 a ;eq1=sym('x1^2+x2=a')eq2=sym('x1-a*x2=0')[x1 x2]=solve(eq1,eq2,x1,x2)v=solve(eq1,eq2)v.x1v.x2an1=x1(1),an2=x1(2)an3=x2(1),an4=x2(2)080求解微分方程:[y]=dsolve('Dy=-y^2+6*y','y(0)=1','x')s=dsolve('Dy=-y^2+6*y','y(0)=1','x')[u]=dsolve('Du=-u^2+6*u','u(0)=1')w=dsolve('Du=-u^2+6*u','z')[u,w]=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z') v=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z')081各种显现隐含函数绘图:f=sym('x^2+1')subplot(221)ezplot(f,[-2,2])subplot(222)ezplot('y^2-x^6-1',[-2,2],[0,10])x=sym('cos(t)')y=sym('sin(t)')subplot(223)ezplot(x,y)z=sym('t^2')subplot(224)ezplot3(x,y,z,[0,8*pi])082极坐标图:r=sym('4*sin(3*x)')ezpolar(r,[0,6*pi])083多函数在一个坐标系内:x=0:0.1:8;y1=sin(x);subplot(221)plot(x,y1)subplot(222)plot(x,y1,x,y2)w=[2 3;3 1;4 6]subplot(223)plot(w)q=[4 6:3 5:1 2]subplot(224)plot(w,q)084调整刻度图像:x=0:0.1:10;y1=sin(x);y2=exp(x);y3=exp(x).*sin(x);subplot(221)plot(x,y2)subplot(222)loglog(x,y2)subplot(223)plotyy(x,y1,x,y2)085等高线等图形,三维图:t=0:pi/50:10*pi;subplot(2,3,1)plot3(t.*sin(t),t.*cos(t),t.^2) grid on[x,y]=meshgrid([-2:0.1:2])z=x.*exp(-x.^2-y.^2)subplot(2,3,2)plot3(x,y,z)box offsubplot(2,3,3)meshz(x,y,z)subplot(2,3,4)surf(x,y,z)contour(x,y,z)subplot(2,3,6)surf(x,y,z)subplot(2,3,5)contour(x,y,z)box offsubplot(2,3,6)contour3(x,y,z)axis off086统计图Y=[5 2 1;8 7 3;9 8 6;5 5 5;4 3 2]subplot(221)bar(Y)box offsubplot(222)bar3(Y)subplot(223)barh(Y)subplot(224)bar3h(Y)087面积图Y=[5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];subplot(221)area(Y)grid onset(gca,'Layer','top','XTick',1:5)sales=[51.6 82.4 90.8 59.1 47.0];x=90:94;profits=[19.3 34.2 61.4 50.5 29.4];subplot(222)area(x,sales,'facecolor',[0.5 0.9 0.6], 'edgecolor','b','linewidth',2) hold onarea(x,profits,'facecolor',[0.9 0.85 0.7], 'edgecolor','y','linewidth',2) hold offset(gca,'Xtick',[90:94])set(gca,'layer','top')gtext('\leftarrow 销售量') gtext('利润')gtext('费用')xlabel('年','fontsize',14)088函数的插值:x=0:2*pi;y=sin(x);xi=0:0.1:8;yi1=interp1(x,y,xi,'linear')yi2=interp1(x,y,xi,'nearest') yi3=interp1(x,y,xi,'spline')yi4=interp1(x,y,xi,'cublic')p=polyfit(x,y,3)yy=polyval(p,xi)subplot(3,2,1)plot(x,y,'o')subplot(3,2,2)plot(x,y,'o',xi,yy)subplot(3,2,3)plot(x,y,'o',xi,yi1)subplot(3,2,4)plot(x,y,'o',xi,yi2)subplot(3,2,5)plot(x,y,'o',xi,yi3)subplot(3,2,6)plot(x,y,'o',xi,yi4)089二维插值计算:[x,y]=meshgrid(-3:0.5:3);z=peaks(x,y);[xi,yi]=meshgrid(-3:0.1:3); zi=interp2(x,y,z,xi,yi,'spline') plot3(x,y,z)hold onmesh(xi,yi,zi+15)hold offaxis tight090函数表达式;function f=exlin(x)if x<0f=-1;elseif x<1f=x;elseif x<2f=2-x;elsef=0;end091:硬循环语句:n=5;for i=1:nfor j=1:nif i==ja(i,j)=2;elsea(i,j)=0;endendendwhile 循环语句:n=1;while prod(1:n)<99^99;n=n+1endn:092 switch开关语句a=input('a=?')switch acase 1disp('It is raning') case 0disp('It do not know')case -1disp('It is not ranging')otherwisedisp('It is raning ?')end093画曲面函数:x1=linspace(-3,3,30)y1=linspace(-3,13,34)[x,y]=meshgrid(x1,y1);z=x.^4+3*x.^2-2*x+6-2*y.*x.^2+y.^2-2*y; surf(x,y,z)。
matlab大作业实验报告,《Matlab程序设计》期末实验报告-大作业2015.doc

matlab⼤作业实验报告,《Matlab程序设计》期末实验报告-⼤作业2015.doc《MATLAB程序设计》实验报告学院: 学号: 姓名:⼀、题⽬:1、(10分)已知矩阵,⽤Matlab代码实现以下要求:(1)将矩阵赋给变量A,并在屏幕上显⽰A;(2)将A按列进列逆序重排,重排后的矩阵赋给变量B,并在屏幕上显⽰B;(3)⽤reshape命令将A重排为⼀个2⾏6列矩阵并赋给变量C;(4)将A重排为⼀个列向量,将其赋给变量D,求D的平均值,在屏幕上显⽰D和它的平均值;(5)⽤命令查看变量A的维数,并显⽰运⾏结果。
2、(10分)写代码实现以下要求:构造菜单项‘Plot’,菜单项Plot有两个⼦菜单项Plot sin(选择此项后执⾏画出曲线,线型为虚线,线条颜⾊为红⾊)和Plot cos(选择此项后执⾏画出曲线 ,线型为实线,线条宽度为2)。
3、(20分)已知,实现下列操作:(1)在同⼀个图形窗⼝,同⼀坐标系下⽤不同的颜⾊和线型绘制三条曲线,并添加图例来区分三条曲线(5分)。
(2)⽤subplot命令,以⼦图的⽅式绘制三条曲线,图形排列⽅式为三⾏⼀列(5分)。
(3) 分别⽤直⽅图(bar)、棒状图(stem)和填充图(fill)绘制三条曲线,以⼦图⽅式绘制,排列⽅式为3⾏3列,共9幅⼦图(10分)。
4、(10分)⽤surf命令绘制曲⾯图形,⽤shading interp命令进⾏插值着⾊处理并添加垂直颜⾊棒。
5、(15分)⾃2011年9⽉1⽇起,我国实⾏新的个⼈所得税征收办法,起征点为3500元,请⽤If-else if-else-end结构实现⼈⼯输⼊⽉收⼊后能计算出个⼈所得税的缴纳额并显⽰⽉收⼊10000元时应缴纳的税款。
级数应纳税所得额x(元)税率备注1x<=15003%x指⽉收⼊扣除起征点3500元之后的余额;215008000045%同上6. (10分)⽤while-end循环结构计算级数和的值,输⼊n值,能计算出f的值,并显⽰结果。
哈工大材料力学大作业--matlab编程

H a r b i n I n s t i t u t e o f T e c h n o l o g y材料力学上机作业课程名称:材料力学设计题目:应力状态分析院系:机电学院班级:分析者:学号:指导教师:***设计时间:2013年6月18日哈尔滨工业大学材料力学上机课设计说明书一, 设计题目题目7 应力状态分析 输入:1. 平面应力状态输入:x y xy σστ(,,);某截面方位角α2. 空间应力状态输入:,x y z xy yz zx σσστττ(,,,,)输出: 1. 输出主应力123σσσ(,,)2. 最大切应力(13max 132σσττ-==)3.如为平面应力状态则需要输出方位角α斜截面上的应力ααστ、及主方向角*σα4. 画出应力圆示意图二, 程序计算设计过程1. 平面应力状态分析对于任意平面应力状态,有max min σσ=2x y σσ+±主应力为:1max 23min ,0,σσσσσ===并且由 2tan 2xyx yστασσ=-可求得主应力方向角13σσαα、。
对于任意一个方位角α,有:=cos 2sin 222sin 2cos 22x yx yxy x yxy αασσσσσατασστατα++++-=-+从而,输入任意角α,即可求得该截面的应力状态ααστ、并且ααστ、都是关于α的函数,上式即为应力圆的参数方程,参数为α。
将α从0到pi 取一系列的值,则可以求出一系列的ααστ、,在坐标系中找到对应点,连接即可作出应力圆。
2. 三向应力状态分析解特征方程 321230I I I σσσ-+-=即可求出主应力123σσσ、、 其中:123||||||||x y z xyx y zy z xz xy y yz z zx x x yx zx xyy zy xzyz z I I I σσσστστσττστστσστττστττσ=-+⎛⎫⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎪= ⎪ ⎪⎝⎭再由 13max 132σσττ-== 可求得最大切应力。
哈理工自动化大四MATLAB实验答案

实验一一、打开Matlab软件,点击,进入simulink Library Browser,点击文件---新建----Model选择建立如下simulink模型图。
10320.02s +0.3s +sStep ScopeTransfer Fcn修改单位阶跃模块的参数:step time:0 (阶跃信号起始时间为0时刻)这个值需要设置一下,其余的值都不用改动。
intitial value:0(初值为0);Final value:1(终值为1);Sample time:0 (采样时间)(这一项我没太弄明白,变了几个值,得到的结果没什么变化。
)将求和模块改为+-;将Transfer Fcn模块的参数设为num:[10],den:[0.02 0.3 1 0];(2)simulation菜单star命令开始仿真;(也可使用那个小黑三角的图标工具)(3)双击示波器模块观察波形;(可以使用Autoscale工具,就是那个像望远镜的图标,得到最佳观测效果)二、选择建立如下simulink模型图。
(做书上P139页到145页即可)最后生成实验二 1、时域分析(1)根据下面传递函数模型:绘制其单位阶跃响应曲线并在图上读标注出峰值,求出系统的性能指标。
8106)65(5)(232+++++=s s s s s s G 答案:程序shiyan3_1_1.m (本程序中用到了stepchar 函数,需要按照书后附录D 自己建立stepchar.m )function [pos,tr,ts,tp]=stepchar(g0,delta) [y,t]=step(g0);figer=plot(t,y),grid on [mp,ind]=max(y); dimt=length(t); yss=y(dimt);pos=100*(mp-yss)/yss tp=t(ind) for i=1:dimt if y(i)>=yss tr=t(i); break ; end end ; Tr=trfor i=1:length(y)if y(i)<=(1-delta)*yss|y(i)>=(1+delta)*yss ts=t(i); end end Ts=ts以下是主程序:>> G=tf([5 25 30],[1 6 10 8]); step(G)[pos,tr,ts,tp]=stepchar(G,0.02)figer =1.9670e+003 pos =7.5374 tp =2.2086 Tr =1.4356 Ts =3.6994(2)已知两个线性定常连续系统的传递函数分别为)(1s G 和)(2s G ,绘制它们的单位脉冲响应曲线。
哈工大 材料力学 MATLAB 梁 上机 大作业

本程序只支持静定结构的梁(左端悬臂梁、简支梁)函数输入格式:beamsolver(L,EI,supports,loads,maxdx);参量的输入格式:L=10.0EI=2e8supports={{'f',0},{'v',10.0}} ----左端悬臂梁supports={{'p',2.0},{'r',8.0}} ----简支梁loads={{'f',[2.0,1000]},{'m',[4.0,500]},{'d',[7.0,9.0,3.0,20,100]}}maxdx=0.01输出为V,M,vy,x的一维行向量和三张坐标图----图1:剪力V图,图2:弯矩M图,图3:挠度vy图.范例:悬臂梁:纯受集中力:beamsolver(10.0,2e8,{{'f',0},{'v',10.0}},{{'f',[2.0,1000]}},0.01)纯受集中矩:beamsolver(10.0,2e8,{{'f',0},{'v',10.0}},{{'m',[4.0,500]}},0.01)纯受分布力(格式一):beamsolver(10.0,2e8,{{'f',0},{'v',10.0}},{{'d',[7.0,9.0,3.0,20,100]}},0.01) 纯受分布力(格式二):beamsolver(10.0,2e8,{{'f',0},{'v',10.0}},{{'d',[(7.0:0.01:9.0);(0:0.01:2.0).^2]} },0.01)受混合力:beamsolver(10.0,2e8,{{'f',0},{'v',10.0}},{{'f',[2.0,1000]},{'m',[4.0,500]},{'d', [7.0,9.0,3.0,20,100]}},0.01)简支梁:纯受集中力:beamsolver(10.0,2e8,{{'p',2.0},{'r',8.0}},{{'f',[5.0,1000]}},0.01)纯受集中矩:beamsolver(10.0,2e8,{{'p',2.0},{'r',8.0}},{{'m',[4.0,500]}},0.01)纯受分布力(格式一):beamsolver(10.0,2e8,{{'p',2.0},{'r',8.0}},{{'d',[7.0,9.0,3.0,20,100]}},0.01) 纯受分布力(格式二):beamsolver(10.0,2e8,{{'p',2.0},{'r',8.0}},{{'d',[(7.0:0.01:9.0);(0:0.01:2.0).^2] }},0.01)受混合力:beamsolver(10.0,2e8,{{'p',2.0},{'r',8.0}},{{'f',[5.0,1000]},{'m',[4.0,500]},{'d' ,[7.0,9.0,3.0,20,100]}},0.01)以上范例输出的剪力V图、弯矩M图都经过笔算检验完全正确。
哈工大MATLAB选修课第二次matlab作业
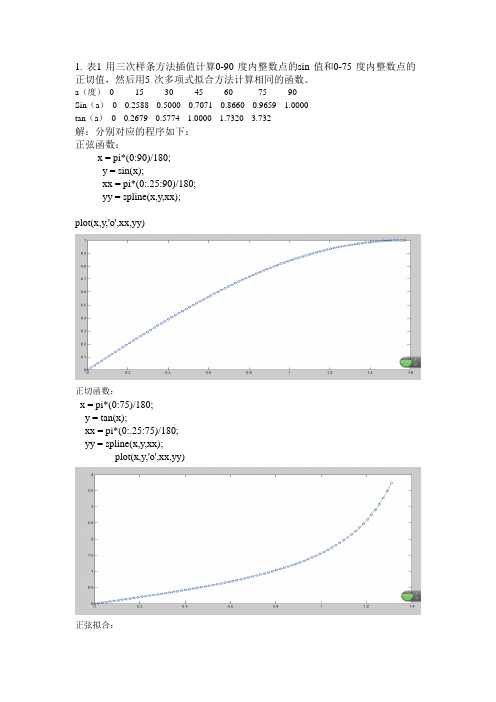
1. 表1 用三次样条方法插值计算0-90 度内整数点的sin 值和0-75 度内整数点的正切值,然后用5 次多项式拟合方法计算相同的函数。
a(度)0 15 30 45 60 75 90Sin(a)0 0.2588 0.5000 0.7071 0.8660 0.9659 1.0000tan(a)0 0.2679 0.5774 1.0000 1.7320 3.732解:分别对应的程序如下:正弦函数:x = pi*(0:90)/180;y = sin(x);xx = pi*(0:.25:90)/180;yy = spline(x,y,xx);plot(x,y,'o',xx,yy)正切函数:x = pi*(0:75)/180;y = tan(x);xx = pi*(0:.25:75)/180;yy = spline(x,y,xx);plot(x,y,'o',xx,yy)正弦拟合:figurex=pi*(0:15:90)/180;y=[0,0.2588,0.5,0.7071,0.866,0.9659,1.0]; xx=pi*(1:0.05:90)/180;p2=polyfit(x,y,5);yy=polyval(p2,xx);plot(x,y,'-ro',xx,yy);正切拟合:figurex=pi*(0:15:75)/180;y=[0,0.2679,0.5774,1,1.732,3.732];xx=pi*(1:0.05:75)/180;p2=polyfit(x,y,5);yy=polyval(p2,xx);plot(x,y,'-ro',xx,yy);legend('描点显示','五次拟合')2. 采用最近点法、线性法和3 次样条法插值计算1-100 整数间平方根n 1 4 9 16 25 36 49 64 81 100Sqtr(n)1 2 3 4 5 6 7 8 9 10解:程序如下:x=[1,4,9,16,25,36,49,64,81,100];y=[1,2,3,4,5,6,7,8,9,10];xx=1:100;yy=interp1(x,y,xx)subplot(2,2,1)plot(x,y,'-ro',xx,yy,'dr');title('线性法');subplot(2,2,2);y2=interp1(x,y,xx,'nearest');plot(x,y,'-ro',xx,y2,'dr');title('最近点法')subplot(2,2,3);y3=interp1(x,y,xx,'spline');plot(x,y,'-ro',xx,y3,'dr');title('3次样条法')仿真的结果:3. 已知p(x)=2x^4-3x^3+5x+13,求p(x)的全部根,由方程p(x)=0 的根构造一个多项式f(x),并和p(x)比较。
材料力学上机大作业(matlab编)

一、可实现课题在如图所示的悬臂梁中,杆件为圆杆。
杆长为L,直径为D,材料弹性模量为E。
输入集中力F大小,作用点a,弯矩M,作用点b,即可求得悬臂梁的挠度曲线图。
二、程序代码clear alldisp('请给定材料信息'); %输入材料信息L=input('圆杆长度L(/M)=');D=input('圆杆直径D(/M)=');E=input('弹性模量E(/GPa)=');I=double(D^4*3.14/32);disp('请给定受力情况'); %输入受力情况F=input('切向集中力大小F(/N)=');a=input('切向集中力作用位置(/M)=');M=input('弯矩大小M(/N*M)=');b=input('弯矩作用位置(/M)=');x1=0:0.01:a; %F引入的挠度vx1=(-F*x1.^2*3*a+F*x1.^3)*(1/(6*E*10^9*I));x2=a:0.01:L;vx2=(-F*a.^2*3*x2+F*a.^3)*(1/(6*E*10^9*I));v11=[vx1,vx2];x11=[x1,x2];x3=0:0.01:b; %M引入的挠度vx3=(-M*x3.^2)*(1/(2*E*10^9*I));x4=b:0.01:L;vx4=(-M*b*x4+M*0.5*b.^2)*(1/(E*10^9*I));x22=[x3,x4];v22=[vx3,vx4];v33=v22+v11; %叠加plot(x11,v33),xlabel('x /M'),ylabel('v(x) /M')title('挠曲线图')grid on;三、使用方法运行代码输入圆杆长度(单位:m)输入圆杆直径(单位:m)输入弹性模量(单位:GPa)输入集中力大小(单位:N)(向下为正,若无请输入0)输入集中力作用位置(单位:m)(若无请输入0)输入弯矩大小(单位:N*m)(逆时针为正,若无请输入0)输入弯矩作用位置(单位:m)(若无请输入0)输出挠曲线图四、运行实例【实例1】圆杆同时受集中力与弯矩作用,输入、输出见下图。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y材料力学上机作业课程名称:材料力学设计题目:应力状态分析院系:机电学院班级:分析者:学号:指导教师:***设计时间:2013年6月18日哈尔滨工业大学材料力学上机课设计说明书一, 设计题目题目7 应力状态分析 输入:1. 平面应力状态输入:x y xy σστ(,,);某截面方位角α2. 空间应力状态输入:,x y z xy yz zx σσστττ(,,,,)输出: 1. 输出主应力123σσσ(,,)2. 最大切应力(13max 132σσττ-==)3.如为平面应力状态则需要输出方位角α斜截面上的应力ααστ、及主方向角*σα4. 画出应力圆示意图二, 程序计算设计过程1. 平面应力状态分析对于任意平面应力状态,有max min σσ=2x y σσ+±主应力为:1max 23min ,0,σσσσσ===并且由 2tan 2xyx yστασσ=-可求得主应力方向角13σσαα、。
对于任意一个方位角α,有:=cos 2sin 222sin 2cos 22x yx yxy x yxy αασσσσσατασστατα++++-=-+从而,输入任意角α,即可求得该截面的应力状态ααστ、并且ααστ、都是关于α的函数,上式即为应力圆的参数方程,参数为α。
将α从0到pi 取一系列的值,则可以求出一系列的ααστ、,在坐标系中找到对应点,连接即可作出应力圆。
2. 三向应力状态分析解特征方程 321230I I I σσσ-+-=即可求出主应力123σσσ、、 其中:123||||||||x y z xyx y zy z xz xy y yz z zx x x yx zx xyy zy xzyz z I I I σσσστστσττστστσστττστττσ=-+⎛⎫⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎪= ⎪ ⎪⎝⎭再由 13max 132σσττ-== 可求得最大切应力。
求解三向应力圆:三个圆121323C 、C 、C 的圆心分别为:231312122313,0,0,0222C C C σσσσσσ+++⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、、半径非别为:231312122313r =,r =,r =222σσσσσσ---由此可以求出三个应力圆的方程,从而作出三向应力圆。
三, 程序代码reg=input('选择应力状态方式(1或2):');%1表示平面应力状态,2表示空间应力状态if reg==1 %选择平面应力状态分析%输入已知量,应力单位为MPa ,转角单位为radcgmx=input('输入x轴方向正应力 cgmx=');cgmy=input('输入y轴方向正应力 cgmy=');txy=input('输入切应力 txy=');%求解主应力、主方向及最大剪应力并输出cgm1=(cgmx+cgmy)/2+(((cgmx-cgmy)/2)^2+txy^2)^(1/2);cgm2=0;cgm3=(cgmx+cgmy)/2-(((cgmx-cgmy)/2)^2+txy^2)^(1/2);tm=(cgm1-cgm3)/2;aerfc=(1/2)*atan(2*txy/(cgmx-cgmy));cgmt=(cgmx+cgmy)/2+(cgmx-cgmy)*cos(2*aerfc)/2+txy*sin(2*aerfc);if cgmt==cgm1;aerfc1=aerfc;aerfc3=aerfc+pi/2;elseaerfc3=aerfc;aerfc1=aerfc+pi/2;enddisplay('主应力为:');display(cgm1);display(cgm2);display(cgm3);display('主方向为:');display(aerfc1);display(aerfc3);display('最大切应力为:');display(tm);% 求解任意截面上的应力aerfa=input('输入截面方位(以弧度表示) aerfa=');cgmr=(cgmx+cgmy)/2+(cgmx-cgmy)*cos(2*aerfa)/2+txy*sin(2*aerfa);tr=-(cgmx-cgmy)*sin(2*aerfa)/2+txy*cos(2*aerfa);display('截面处应力状况:');display('正应力:');display(cgmr);display('切应力:');display(tr);%求解应力圆并作图i=0;for theta=0:pi/200:picgmt=(cgmx+cgmy)/2+(cgmx-cgmy)*cos(2*theta)/2+txy*sin(2*theta); tt=-(cgmx-cgmy)*sin(2*theta)/2+txy*cos(2*theta);i=i+1;CG(i)=cgmt;TT(i)=tt;plot(CG,TT),axis equal;title('应力圆');xlabel('正应力cgm/ MPa');ylabel('切应力t/MPa');grid on;endelseif reg==2 %选择三向应力状态分析%输入已知量,应力单位为MPa,转角单位为radcgmx=input('输入x轴方向正应力 cgmx=');cgmy=input('输入y轴方向正应力 cgmy=');cgmz=input('输入y轴方向正应力 cgmz=');txy=input('输入切应力 txy=');tyz=input('输入切应力 tyz=');tzx=input('输入切应力 tzx=');%求解主应力及最大剪应力并输出I1=cgmx+cgmy+cgmz;I2=det([cgmx,txy;txy,cgmy])+det([cgmy,tyz;tyz,cgmz])+det([cgmz,tzx;tzx,c gmx]);I3=det([cgmx,txy,tzx;txy,cgmy,tyz;tzx,tyz,cgmz]);syms x;ffp=x^3-I1*x^2+I2*x-I3;cgm=solve(ffp);cgm=eval(cgm);cgm1=max(cgm(1),cgm(2));cgm1=max(cgm1,cgm(3));cgm3=min(cgm(1),cgm(2));cgm3=min(cgm3,cgm(3));cgm2=cgm(1)+cgm(2)+cgm(3)-cgm1-cgm3;tm=(cgm1-cgm3)/2;display('主应力为:');display(cgm1);display(cgm2);display(cgm3);display('最大切应力为:');display(tm);%求解应力圆并作图i=0;r12=(cgm1-cgm2)/2;r23=(cgm2-cgm3)/2;r13=(cgm1-cgm3)/2;x12=(cgm1+cgm2)/2;x23=(cgm2+cgm3)/2;x13=(cgm1+cgm3)/2;for theta=0:pi/200:2*pi X12=x12+r12*cos(theta); Y12=r12*sin(theta); X23=x23+r23*cos(theta); Y23=r23*sin(theta); X13=x13+r13*cos(theta); Y13=r13*sin(theta); i=i+1;XX12(i)=X12;YY12(i)=Y12;XX23(i)=X23;YY23(i)=Y23;XX13(i)=X13;YY13(i)=Y13; plot(XX12,YY12,XX23,YY23,XX13,YY13),axis equal;title('三向应力圆');xlabel('正应力cgm/ MPa');ylabel('切应力t/MPa');grid on;text(x12,0,'C12');text(x23,0,'C23');text(x13,0,'C13'); end elsedisplay('选择方式错误!'); end四, 程序说明程序运行后,首先给reg 变量赋值,选择应力状态方式,其中reg=1位平面应力状态,reg=2为三向应力状态。
若输入reg 为其他值,则会显示“选择方式错误!”。
1.平面应力状态若选择平面应力状态,则需要输入:正应力cgmx 、cgmy 以及切应力txy 。
然后程序就会自动输出三个主应力:cgm1、cgm2、cgm3以及主应力方向角:aerfc1、aerfc3,和最大切应力:tm ,进一步输入任意截面方向角:aerfa ,即可求出该截面的正应力:cgmr ,切应力:tr 。
同时作出应力圆的图像。
2.三向应力状态若选择三向应力状态,则需要输入:正应力cgmx 、cgmy 、cgmz ,以及切应力txy 、tyz 、tzx 。
然后程序会自动输出三个主应力:cgm1、cgm2、cgm3,以及最大切应力tm 。
同时作出三向应力圆的图像。
五, 举例验证例1.选择平面应力状态,已知=x y xy σστ40MPa,=-20MPa,=40MPa ,求主应力、主方向、最大切应力以及6πα=斜截面上的应力,并作出应力圆。
例2.选择空间应力状态,已知:=6a =20M =2=-4=0,=0x y z xy yz zx MPa σσστττ0MP ,Pa,0MPa,0MPa,MPa求主应力及最大切应力,并作出应力圆。
(材料力学第二单元课后第13题)收获感悟:做这个材料大作业,虽然花费了很长时间,但是我感到收获很多。
在此过程中,我对MATLAB从一无所知到熟练编辑,甚至接触到对界面编辑,这将成为我一生的财富,MATLAB也必将成为我日后工作的得力助手。
我为能有一次这样锻炼的机会而感到幸运,希望以后还会更多这样的机会充实自己。
对于应力分析部分,我想也会因为这次程序的编写而理解的更加深刻。
不足之处在于因时间关系,没有完全编出界面。
所呈现的界面还不能进行运算。
