Cohen-Sutherland直线剪裁算法
计算机图形学Cohen-Sutherland直线裁剪算法源码c++
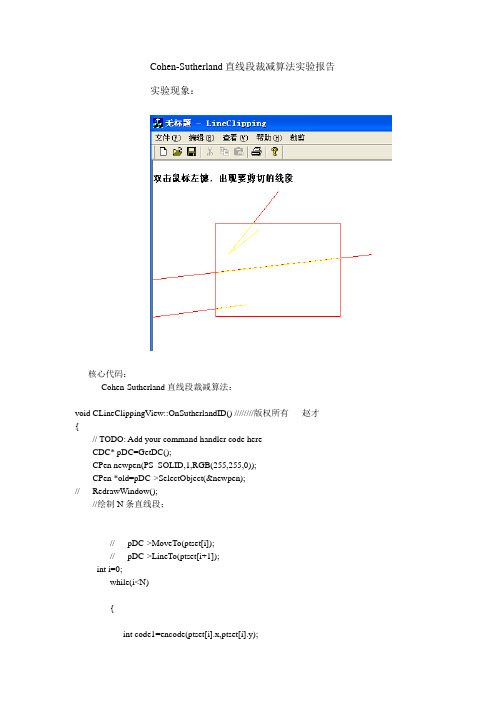
实验现象:
核心代码:
Cohen-Sutherland直线段裁减算法:
void CLineClippingView::OnSutherlandID() ////////版权所有赵才
{
// TODO: Add your command handler code here
pDC->LineTo(ptset[i+1]);
i+=2;
continue;
}
else
{
if((code1 & code2)!=0)//简弃
{
i+=2;
continue;
}
else
{
if(code1==0)
{
int tx,ty,ct;
ct=code1;
code1=code2;
code2=ct;
tx=ptset[i].x;
ptset[i].y=YT;
continue;
}
if(code1 & BOTTOM)
{
//
ptset[i].x=int(1.0/k*(YB-ptset[i].y)+ptset[i].x+0.5);
ptset[i].y=YB;
continue;
}
}
}
}
}
int encode(int x,int y) //确定端点编码
if(code1 & LEFT)
{
//
ptset[i].y=int(k*(XL-ptset[i].x)+ptset[i].y+0.5);
ptset[i].x=XL;
描述cohen sutherland裁剪算法

描述cohen sutherland裁剪算法
Cohen-Sutherland裁剪算法是一种用于裁剪线段的算法,由S.G.Cohen和D.P.Sutherland在1969年提出。
它的基本思想是使用一个2D窗口矩形对要裁剪的线段进行测试,根据结果将线段分成四个不同的类别(左端点的左边,右端点的右边,上端点的上边,下端点的下边),这样就可以把线段按照它们在窗口中的相对位置编码。
下面具体讲解Cohen-Sutherland裁剪算法的步骤:
1.首先,确定要裁剪的线段端点的坐标,以及窗口的左上角和右下角的坐标。
2.然后,根据左上角的坐标和右下角的坐标,利用一个4位的二进制整数对线段端点进行编码,每一位的0或1表示端点是否在窗口的4个边界外面。
3.对比端点的编码,如果两个编码都为0,表示线段完全位于窗口内,不需进行裁剪。
如果两个编码不同,则表示至少有一个端点位于窗口边界外,此时需要进行裁剪。
4.根据不同的编码情况,对线段进行裁剪:
(1)如果两个编码都不为0,则表明线段两个端点都在窗口边界外,此时线段不可见,可以将线段丢弃。
(2)如果两个编码中只有一个不为0,则表明线段上有一个端点在窗口边界外,此时只需要将外部端点移动到窗口边界上,即可得到一个可见的线段。
5.此外,还需要对线段两个端点进行重新编码,根据编码重复步
骤3和步骤4,直至线段完全位于窗口内,或者线段完全被丢弃。
至此,Cohen-Sutherland裁剪算法就完成了。
它既可以用于直线的裁剪,也可以用于曲线的裁剪。
cohen-sutherland裁剪算法例题

cohen-sutherland裁剪算法例题一、算法简介Cohen-Sutherland裁剪算法是一种用于图像处理的算法,用于确定一个像素点是否被剪裁,即是否需要被剔除。
该算法基于一个简单的原理:对于一个像素点,如果它的坐标位于某个特定区域(例如矩形区域)之外,那么它就不属于原始图像的裁剪区域,可以被剔除。
二、算法步骤1.初始化:设定一个裁剪区域的起始坐标(xmin,ymin)和结束坐标(xmax,ymax)。
2.将裁剪区域的坐标转化为四舍五入的整数坐标(xm,ym,xm+1,ym+1)。
3.判断像素点(x,y)是否在裁剪区域内:a.如果(x>=xminandx<=xmaxandy>=yminandy<=ym),则像素点在裁剪区域内。
b.否则,像素点不在裁剪区域内。
4.根据像素点的位置,确定是否需要剔除该像素点:a.如果像素点在裁剪区域内,则保留该像素点。
b.如果像素点不在裁剪区域内,则剔除该像素点。
三、算法应用Cohen-Sutherland裁剪算法在图像处理中非常有用,它可以有效地剔除不需要的像素点,提高图像的质量和清晰度。
例如,在图像缩放、剪裁、滤镜处理等操作中,都需要用到Cohen-Sutherland裁剪算法。
四、例题实现以下是一个使用Python实现的Cohen-Sutherland裁剪算法的例子:```pythondefcohen_sutherland(image,xmin,ymin,xmax,ymax):#将坐标转化为四舍五入的整数坐标xm,ym=int(xmin),int(ymin)xm_next,ym_next=int(xmax),int(ymax)+1#加上1是为了避免下溢image_clipped=[list(i)foriinimage]#创建一个新的列表用于存放裁剪后的图像数据foriinrange(len(image)):forjinrange(len(image[i])):if(j>=ymori>=xmorj<ym_next-ymori<xm_next-xm):#如果像素点不在裁剪区域内image_clipped[i][j]=""#剔除该像素点,用空格代替else:#在裁剪区域内,保留该像素点image_clipped[i][j]=image[i][j]#不作任何修改returnimage_clipped```五、示例应用以下是一个使用Cohen-Sutherland裁剪算法进行图像剪裁的示例:假设有一张名为"input.jpg"的图像,要将其中的一部分剪裁掉。
[计算机图形学]复习Cohen-Sutherland直线段裁剪算法
![[计算机图形学]复习Cohen-Sutherland直线段裁剪算法](https://img.taocdn.com/s3/m/31457f66a88271fe910ef12d2af90242a895ab0f.png)
[计算机图形学]复习Cohen-Sutherland直线段裁剪算法
关于Cohen-Sutherland 直线段裁剪算法思想概述
直线段裁剪是⼆维图形裁剪的基础,本质是判断直线段是否与窗⼝边界相交,如相交则进⼀步确定直线段上位于窗⼝内的部分。
算法思想:直线的端点赋予⼀组4位⼆进制码,称为RC(区域编码),裁剪窗⼝的四条边所在的直线可以把平⾯分为9个区域,对各个区域的编码也是四位,C3C2C1C0,分别代表上下右左四个窗⼝边界。
裁剪窗⼝所在的区域为0000,对于直线段上的端点进⾏编码,等于该端点所在的区域的编码。
编码后就容易判断两个端点的情况:
⽐如两个端点求与不等于0,即RC0&RC1≠0;说明该线段在裁剪窗⼝之外,应简弃;
两个端点RC编码按位或为0,即RC0|RC1=0。
说明直线段两个端点都在窗⼝内,应简取。
还有第三种情况:不满⾜前两种情况的,说明直线段与边界或其延长线有交点,要进⾏求交判断:
①此时直线段与边界相交,P0P1和两个边界相交,按左右下上的顺序计算交点,设交点为P,注意:总是要让直线段的⼀个顶点处于窗⼝之外,例如P0点。
这样P0点到交点P的直线段必然不可见,故可以将交点外的线段简弃。
②直线段与边界的延长线相交,直线段在窗⼝外,也不在窗⼝同⼀侧。
依旧按照左右下上顺序计算,将延长线与线段交点定为P,有PP0,位于窗⼝某侧,被简弃。
如果求裁剪后窗⼝内直线段的端点坐标,(那⼀般是求P1,以实际题⽬为准,看剪了哪部分),两点求直线⽅程,然后带⼊相交边界的x或y值可得。
Cohen-Sutherland裁剪算法

Cohen-Sutherland裁剪算法#include <iostream>#include <windows.h>#include <gl/glut.h>using namespace std;#include <GL/glut.h>#include <cstdio>#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8int x1=150,y1=50, x2=50, y2=250, XL=100, XR=300, YB=100, YT=200; //(x1,y1)、(x2,y2)为直线段的端点,XL为左边界,XR为右边界,YB为下边界,YT为上边界int x1_init = 150, y1_init = 50, x2_init = 50, y2_init = 250; //将直线段端点备份,以便画出裁剪前的直线段int encode(int x,int y){int c = 0;if (x < XL) c |= LEFT;if (x > XR) c |= RIGHT;if (y < YB) c |= BOTTOM;if (y > YT) c |= TOP;return c;}void CS_LineClip() //Cohen-Sutherland裁剪算法{int x, y;int code1, code2, code;code1 = encode(x1, y1);code2 = encode(x2, y2);while (code1 != 0 || code2 != 0){if (code1 & code2)return;if (code1 != 0)code = code1;elsecode = code2;if (LEFT & code){x = XL;y = y1 + (y2 - y1)*(XL - x1) / (x2 - x1);}else if (RIGHT & code){x = XR;y = y1 + (y2 - y1)*(XR - x1) / (x2 - x1);}else if (BOTTOM & code){y = YB;x = x1 + (x2 - x1)*(YB - y1) / (y2 - y1);}else if (TOP & code){y = YT;x = x1 + (x2 - x1)*(YT - y1) / (y2 - y1);}if (code == code1){x1 = x; y1 = y; code1 = encode(x1, y1);}else{x2 = x; y2 = y; code2 = encode(x2, y2);}}}void init() //初始化函数{glClearColor(1.0, 1.0, 1.0, 0.0); //设置背景颜⾊glMatrixMode(GL_PROJECTION); // 设置投影参数 gluOrtho2D(0.0, 600.0, 0.0, 400.0); // 设置场景的⼤⼩ CS_LineClip(); //执⾏⼀次裁剪算法}void mydisplay() //显⽰函数{//绘制⽅形边界glClear(GL_COLOR_BUFFER_BIT);glColor3f(1.0, 0.0, 0.0);glPointSize(2);glBegin(GL_LINE_LOOP);glVertex2i(XL, YT);glVertex2i(XL, YB);glVertex2i(XR, YB);glVertex2i(XR, YT);glEnd();glFlush();//绘制未裁剪前的线段glBegin(GL_LINES);glVertex2i(x1_init, y1_init);glVertex2i(x2_init, y2_init);glEnd();glFlush();//绘制裁剪后的线段glColor3f(0.0, 0.0, 0.0);glBegin(GL_LINES);glVertex2i(x1, y1);glVertex2i(x2, y2);glEnd();glFlush();}int main(int argc, char *argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE); glutInitWindowPosition(100, 100);glutInitWindowSize(400, 400);glutCreateWindow("Cohen-Sutherland裁剪算法");init();glutDisplayFunc(&mydisplay);glutMainLoop();return 0;}。
计算机图形学实验Cohen-Sutherland算法

实验5-6一、实验题目请按照图5-32所示,使用对话框输入直线段的起点和终点坐标。
在屏幕客户区左侧区域绘制输入直线段和“窗口”,在屏幕客户区右侧区域绘制“视区”并输出裁剪结果。
这里需要用到窗视变换公式。
请使用Cohen-Sutherland 算法编程实现。
二、实验思想Cohen-Sutherland 直线裁剪算法是最早流行的编码算法。
每条直线的端点都被赋予一组四位二进制代码,称为区域编码(Region Code ,RC),用来标识直线端点相对于窗口边界及其延长线的位置。
假设窗口是标准矩形,由上(y=w yt )、下(y=w yb )、左(x=w xl )、右(x=w xr )四条边组成,如图5-23所示。
延长窗口四条边形成9个区域,如图5-24所示。
这样根据直线的任一端点P(x,y)所处的窗口区域位置,可以赋予一组4位二进制区域码RC =C 4C 3C 2C 1。
w yb w yt wxr w xl为了保证窗口内直线端点的编码为零,编码规则定义如下:第一位:若端点位于窗口之左侧,即x<w xl,则C1=1,否则C1=0。
第二位:若端点位于窗口之右侧,即x>w xr,则C2=1,否则C2=0。
第三位:若端点位于窗口之下侧,即y<w yb,则C3=1,否则C3=0。
第四位:若端点位于窗口之上侧,即y>w yt,则C4=1,否则C4=0。
裁剪步骤如下:(1)若直线的两个端点的区域编码都为零,即RC1|RC2=0,说明直线两端点都在窗口内,应“简取”之。
(2)若直线的两个端点的区域编码都不为零,即RC1&RC2≠0,即直线位于窗外的同一侧,说明直线的两个端点都在窗口外,应“简弃”之。
(3)若直线既不满足“简取”也不满足“简弃”的条件,直线必然与窗口或窗口边界的延长线相交,需要计算直线与窗口边界的交点。
交点将直线分为两段,其中一段完全位于窗口外,可“简弃”之。
对另一段重复进行上述处理,直至该直线段完全被舍弃或找到完全位于窗口内的直线段为止。
计算机图形学实验指导书--实验2使用线段剪裁

实验2使用线段剪裁Cohen——sutherland算法一.实验目的及要求根据Cohen——sutherland算法,掌握直线剪裁的程序设计方法。
注意,不能使用语言库中的画圆函数。
二.理论基础将不需要裁剪的直线挑出,并删去其中在窗外的直线,然后对其余直线,逐条与窗框求交点,并将窗框外的部分删去。
采用Cohen-Sutherland直线剪裁的算法一区域编码为基础,将窗口及周围的八个方向以4位的二进制数进行编码。
4个位分代表窗外上,下,左右的编码值。
三、算法分析1. Cohen—SutherLand直线裁剪算法裁剪的实质,就是决定图形中那些点、线段、文字、以及多边形在窗口之内。
Cohen—SutherLand直线裁剪算法的基本大意是:对于每条线段P1P2,分为三种情况处理。
1) 若P1P2完全在窗口内,则显示该线段P1P2,简称“取”之。
2) 若P1P2明显在窗口外,则丢弃该线段P1P2,简称“弃”之。
3) 若线段既不满足“取”的条件,也不满足“弃”的条件,则把线段分为两段。
其中一段完全在窗口外,可弃之。
然后对另一段重复上述处理。
为了使计算机能够快速地判断一条线段与窗口属何种关系,采用如下的编码方法。
延长窗口的边,把未经裁剪的图形区域分为9个区,每个区具有一个四位代码,即四位二进制数,从左到右各位依次表示上、下、左、右。
裁剪一条线段时,先求出端点P1P2所在的区号code1和code2。
若code1=0且code2=0,则说明P1和P2均在窗口内,那么整条线段也比在窗口内,应取之。
若code1和code2经按位与运算后的结果code1&code2不为0,则说明两个端点同在窗口的上方、下方、左方或右方。
若上述两种条件均不成立,则按第三种情况处理,求出线段与窗口某边的交点,在交点处把线段一分为二,其中必有一段完全在窗口外,可以弃之。
再对另一段重复进行上述处理。
计算线段与窗口边界(或其延长线)的交点,属于线段与直线求交问题。
裁剪算法——cohen-sutherland算法

裁剪算法——cohen-sutherland算法实验环境:VC6.0算法思想: 延长窗⼝的边,将⼆维平⾯分成9个区域,每个区域赋予4位编码C t C b C r C l,裁剪⼀条线段P1P2时,先求出所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗⼝内,应取之。
若按位与运算code1&code2,则说明两个端点同时在窗⼝的上⽅、下⽅、左⽅或右⽅,则可判断线段完全在窗⼝外,可弃之;否则,按第三种情况处理,求出线段与窗⼝某边的交点,在交点处把线段⼀分为⼆,其中必有⼀段在窗⼝外,可弃之,再对另⼀段重复上述处理。
100110001010000100000010010********* 多边形裁剪编码程序实现:#include "stdafx.h"#include<stdio.h>#include<conio.h>#include<graphics.h>#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8void midpointLine(int x0,int y0,int x1,int y1,int color)//中点画线算法{int a,b,d1,d2,d,x,y;a=y0-y1;b=x1-x0;d=2*a+b;d1=2*a;d2=2*(a+b);x=x0;y=y0;putpixel(x,y,color);while(x<x1){if(d<0){x++;y++;d+=d2;}else{x++;d+=d1;}putpixel(x,y,color);}}int encode(int x,int y,int XL,int XR,int YB,int YT)//编码{int c=0;if(x<XL) c|=LEFT;if(x>XR) c|=RIGHT;if(y<YB) c|=BOTTOM;if(y>YT) c|=TOP;return c;}void C_SLineClip(int x1,int y1,int x2,int y2,int XL,int XR,int YB,int YT){int code1,code2,code,x,y;code1=encode(x1,y1,XL,XR,YB,YT);code2=encode(x2,y2,XL,XR,YB,YT);while((code1 != 0) || (code2 != 0)){if((code1 & code2) != 0){midpointLine(x1,y1,x2,y2,RGB(0, 255, 0));//如果直线在裁剪窗⼝外就⽤绿⾊画出printf("线段在窗⼝外!");return;}if(code1 != 0) code=code1;else code=code2;if((LEFT & code) != 0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if((RIGHT & code) != 0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}else if((BOTTOM & code) != 0){y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1);}else if((TOP & code) != 0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if(code == code1){x1=x; y1=y; code1=encode(x,y,XL,XR,YB,YT);}else{x2=x; y2=y; code2=encode(x,y,XL,XR,YB,YT);}}midpointLine(x1,y1,x2,y2,RGB(255,0,0));//将裁减的直线⽤红⾊标注return;}int main(int argc, char* argv[]){int gdriver=DETECT,gmode;int x1=20,y1=30,x2=250,y2=300,XL=10,XR=200,YT=400,YB=30;initgraph(&gdriver,&gmode,"c:\\tc");//setbkcolor(WHITE);cleardevice();midpointLine(x1,y1,x2,y2,RGB(0,255,0));//将被裁剪直线⽤绿⾊画出rectangle(10,400,200,30);//rectangle(int left,int top,int right,int bottom);//裁剪窗⼝ C_SLineClip(x1,y1,x2,y2,XL,XR,YB,YT);// cohen sutherland算法getch();closegraph();return0;}显⽰效果:将在窗⼝内的线段设为红⾊,窗⼝外的线段设为绿⾊。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)onside(int[]):该方法判断直线两端点是否在区域内
(4)outside(int[]):该方法判断直线是否在同一端
(5)cutYourLine(int,int,int,int):该方法用于获取直线与区域的两个交点坐标
实验总结以及心得体会:
评定成绩:批阅老师:2017年月日
附页:
(1)paintComoponet(Graphics):void ,该方法主要用于画图,通过调用encode(int,int,int,int)方法、onside(int[])方法、outside(int[])方法和cutYourLIne(int,int,int,int)方法判断直线的类型和获取在区域内的两个直线端点坐标,画出区域内的直线
实验报告
专业:软件工程班级:学号:姓名:
课程名称:图形图像处理2017– 2017年度第2学期
课程类别:专业选修实验时间:2017年月日
实验名称:Cohen-Suths7 , Windows XP等都可,
使用Eclipse做实验。
实验目的和要求:
编写线段裁剪算法程序,验证算法的正确性
实验内容:
对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗口内,则显示该线段P1P2简称“取”之。
(2)若P1P2明显在窗口外,则丢弃该线段,简称“弃”之。
(3)若线段既不满足“取”的条件,也不满足“弃”的条件,则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理。
实验截图如下:
