传送带模型
动力学中的典型传送带模型-高三

“传送带”模型1.水平传送带模型项目图示运动情况判断方法情景1可能一直加速,也可能先加速后匀速若v22μg≤l,物、带能共速情景2当v0>v时,可能一直减速,也可能先减速再匀速;当v0<v时,可能一直加速,也可能先加速再匀速若|v2-v20|2μg≤l,物、带能共速情景3传送带较短时,滑块一直减速达到左端;传送带较长时,滑块还要被传送带传回右端若v202μg≤l,物块能返回2.倾斜传送带模型项目图示运动情况判断方法情景1可能一直加速,也可能先加速后匀速若v22a≤l,物、带能共速情景2可能一直加速,也可能先加速后匀速,还可能先以a1加速后以a2加速若v22a≤l,物、带能共速;若μ≥tan θ,物、带共速后匀速;若μ<tan θ,物体以a2加速(a2<a)(1)解题关键1:对物体所受的摩擦力进行正确的分析判断。
(2)解题关键2:物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻。
【例2】(多选)如图所示,绷紧的水平传送带足够长,且以v1=2 m/s的恒定速率运行。
初速度大小v2=3 m/s的小墨块从与传送带等高的光滑水平地面(图中未画出)上的A处滑上传送带,墨块可视为质点。
若从墨块滑上传送带开始计时,墨块在传送带上运动5 s后与传送带的速度相同,则()A.墨块与传送带速度相同之前,受到传送带的摩擦力方向水平向右B.墨块在传送带上滑行的加速度大小a=0.2 m/s2C.墨块在传送带上留下的痕迹长度为4.5 mD.墨块在传送带上留下的痕迹长度为12.5 m【拓展提升1】若将【例2】中的v1、v2的值改为v1=3 m/s,v2=2 m/s,求墨块在传送带上留下的痕迹长度。
考向倾斜传送带解决倾斜传送带问题时要特别注意mg sin θ与μmg cos θ的大小和方向的关系,进一步判断物体所受合力与速度方向的关系,确定物体运动的情况。
【例3】(多选)如图所示,一足够长的倾斜传送带顺时针匀速转动。
(完整版)高中物理传送带模型(解析版)
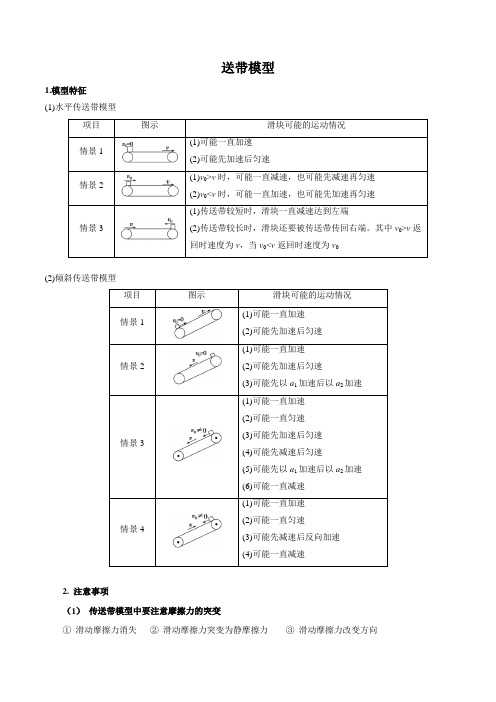
送带模型1.模型特征(1)水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v返回时速度为v,当v0<v返回时速度为v0(2)倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速情景3(1)可能一直加速(2)可能一直匀速(3)可能先加速后匀速(4)可能先减速后匀速(5)可能先以a1加速后以a2加速(6)可能一直减速情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速(4)可能一直减速2. 注意事项(1)传送带模型中要注意摩擦力的突变①滑动摩擦力消失②滑动摩擦力突变为静摩擦力③滑动摩擦力改变方向(2)传送带与物体运动的牵制。
牛顿第二定律中a 是物体对地加速度,运动学公式中S 是物体对地的位移,这一点必须明确。
(3) 分析问题的思路:初始条件→相对运动→判断滑动摩擦力的大小和方向→分析出物体受的合外力和加速度大小和方向→由物体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【典例1】如图所示,传送带的水平部分长为L ,运动速率恒为v ,在其左端无初速放上木块,若木块与传送带间的动摩擦因数为μ,则木块从左到右的运动时间可能是( )A.L v +v 2μgB.L vC.2L μgD.2L v【答案】 ACD【典例2】如图所示,倾角为37°,长为l =16 m 的传送带,转动速度为v =10 m/s ,动摩擦因数μ=0.5,在传送带顶端A 处无初速度地释放一个质量为m =0.5 kg 的物体.已知sin 37°=0.6,cos 37°=0.8,g =10 m/s 2.求:(1)传送带顺时针转动时,物体从顶端A 滑到底端B 的时间; (2)传送带逆时针转动时,物体从顶端A 滑到底端B 的时间. 【答案】 (1)4 s (2)2 s【典例3】如图所示,与水平面成θ=30°的传送带正以v =3 m/s 的速度匀速运行,A 、B 两端相距l =13.5 m 。
高中物理-传送带模型

传送带模型1.水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v,返回时速度为v;当v0<v,返回时速度为v02.倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速*情景3(1)可能一直加速(2)可能先加速后匀速(3)可能一直匀速(4)可能先以a1加速后以a2加速*情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速①水平传送带问题:求解的关键在于正确分析出物体所受摩擦力.判断摩擦力时要注意比较物体的运动速度与传送带的速度,也就是分析物体在运动位移x(对地)的过程中速度是否和传送带速度相等.物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻.②倾斜传送带问题:求解的关键在于正确分析物体与传送带的相对运动情况,从而判断其是否受到滑动摩擦力作用.如果受到滑动摩擦力作用应进一步确定其大小和方向,然后根据物体的受力情况确定物体的运动情况.当物体速度与传送带速度相等时,物体所受的摩擦力有可能发生突变.小结:分析处理传送带问题时需要特别注意两点:一是对物体在初态时(静止释放或有初速度的释放)所受滑动摩擦力的方向的分析;二是对物体与传送带共速时摩擦力的有无及方向的分析.对于传送带问题,一定要全面掌握上面提到的几类传送带模型,尤其注意要根据具体情况适时进行讨论,看一看受力与速度有没有转折点、突变点,做好运动过程的划分及相应动力学分析.3.传送带问题的解题思路模板[分析物体运动过程]例1:(多选)如图所示,足够长的传送带与水平面夹角为θ,在传送带上某位置轻轻放置一小木块,小木块与传送带间动摩擦因素为μ,小木块速度随时间变化关系如图所示,v 0、t 0已知,则( )A .传送带一定逆时针转动B .00tan cos v gt μθθ=+C .传送带的速度大于v 0D .t 0后滑块的加速度为002sin v g t θ-[求相互运动时间,相互运动的位移] 例2:如图所示,水平传送带两端相距x =8 m ,工件与传送带间的动摩擦因数μ=0.6,工件滑上A 端时速度v A =10 m/s ,设工件到达B 端时的速度为v B 。
传送带模型汇总

传送带模型的优势
1 高效性
传送带模型可以实现自动 化传输,节省人力和时间 成本。
2 可靠性
3 可定制性
传送带模型运作稳定,减 少物体损坏和丢失的风险。
传送带模型可以根据需求 进行定制,适应不同物体 和场景。
传送带模型的不足
限制物体尺寸
传送带模型使用有限的尺寸,不适用于过大或过重的物体。
可能占用空间
传送带模型汇总
本演示将介绍传送带模型的定义、基本原理、应用领域、优势、不足、发展 前景,并提供结论和总结。让我们一起探索这个引人入胜的话题。
传送带模型的定义
传送带模型是一种用于物体或信息传递的工程设备,通过连续移动的传送带 将物体从一个地方转移到另一个地方。
传送带模型的Βιβλιοθήκη 本原理1 传送带传送带由驱动装置、张紧装置和传送带材料组成,通过不断循环的运动来传输物体。
传送带模型需要占用一定的空间,对于场地有限的环境不太合适。
传送带模型的发展前景
随着自动化技术和物流需求的不断增长,传送带模型有望在各个行业中得到 更广泛的应用和改进,提升物体传输的效率和准确性。
结论和总结
传送带模型是一种既古老又现代的物体传输技术,它在生产制造、物流和交通等领域发挥着重要作用。我们期 待看到它未来的创新和发展。
2 传送物体
物体被放置在传送带顶部,随着传送带的运动,物体被带到目的地。
传送带模型的应用领域
生产制造
传送带模型广泛用于生产制造行 业,加速生产流程并提高效率。
航空旅行
传送带模型在航空旅行中用于行 李传送系统,方便旅客的行李投 放和取出。
邮政服务
传送带模型被邮政服务用于包裹 分拣和投递,提高速度和准确性。
高三物理知识点传送带模型

高三物理知识点传送带模型高三物理知识点:传送带模型传送带模型是物理学中对运动的描述和解释的一种简化模型。
它常被用来说明物体在平稳运动状态下的变化规律和相关的物理概念。
本文将介绍传送带模型的基本原理和应用,以及与高考物理相关的知识点。
一、传送带模型的基本原理传送带模型基于以下假设:1. 假设传送带平稳运行,即传送带的速度保持不变;2. 假设系统在相对运动中处于稳态,即不受到外力的干扰;3. 假设传送带的运动与物体的运动具有良好的耦合性。
在传送带模型中,我们可以将物体视作一个质点,其运动状态由位置、速度和加速度等因素决定。
通过对物体所受的驱动力和阻力进行分析,可以得到物体在传送带上的运动规律。
二、传送带模型的应用1. 平抛运动:传送带模型可以用来解释物体在水平平面上的平抛运动。
在这种情况下,传送带的速度影响了物体的水平速度,而垂直方向的运动受到重力的影响。
根据传送带模型,物体的横向速度与传送带速度相等,而垂直速度受到重力加速度的影响。
这样,我们可以推导出物体在水平平面上的轨迹、飞行时间和最大高度等参数。
2. 斜抛运动:传送带模型也可以应用于物体在斜面上的抛体运动。
在这种情况下,传送带的速度和斜面的倾角会对物体的运动产生影响。
根据传送带模型,物体的速度可以分解为沿斜面和垂直斜面的分量。
这样,我们可以得到物体在斜面上的运动规律,包括滑动距离、飞行时间和最大高度等参数。
三、与高考物理相关的知识点传送带模型是理解和应用以下高考物理知识点的基础:1. 运动规律:通过传送带模型,我们可以更深入地理解运动物体的速度、加速度和运动规律。
包括匀速直线运动、匀加速直线运动等。
2. 平衡力分析:传送带模型可以帮助我们分析物体所受的平衡力和非平衡力。
比如,在平抛运动中,物体的横向速度受到传送带的平衡力,而垂直速度受到重力的非平衡力。
3. 牛顿定律:传送带模型也可以用来解释和应用牛顿定律。
在斜抛运动中,我们可以分析物体受到的斜面作用力和重力作用力,并根据牛顿定律推导运动方程。
高中物理传送带模型总结

高中物理传送带模型总结开始运动的传送带(b) 、 (c)“传送带模型”1.模型特征 一个物体以速度vO(vO >0)在另一个匀 速运动的物体上 力学系统可看做 模型,如图(a)、 示.2•建模指导水平传送带问题:求解的关键在于对物体所受的摩擦力 进行正确的分析判断•判断摩擦力时要注意比较物体的 运动速度与传送带的速度,也就是分析物体在运动位移 x(对地)的过程中速度是否和传送带速度相等.物体的 速度与传送带速度相等的时刻就是物体所受摩擦力发生 突变的时刻• 水平传送带模型:滑块可能的运融储况芾最1fl T) 〔1」匚能一直加世 〔2)可能先加速后匀速 ⑴话r 时.irk-也可紐碱it 再勺豐时*可能一亘如询,也可能牛加谏再勻谏1•传送带是一种常用的运输工具,被广泛应用于矿山、码头、货场、车站、机场等.如图所示为火车站使用的传送带示意图.绷紧的传送带水平部分长度L=5 m并以v o = 2 m/s的速度匀速向右运动.现将一个可视为质点的旅行包无初速度地轻放在传送带的左端,已知旅行包与传送带之间的动摩擦因数卩= 0.2 , g取10 m/s.(1)求旅行包经过多长时间到达传送带的右端;(2)若要旅行包从左端运动到右端所用时间最短,则传送带速度的大小应满足什么条件?最誉三°短时间是多少?2.如图所示,一质量为m=0.5kg的小物体从足够高的光滑曲面上自由滑下,然后滑上一水平传送带。
已知物体与传送带之间的动摩擦因数为a=0.2,传送带水平部分的长度L=5m,两端的传动轮半径为R=0.2m ,在电动机的带动下始终以3 =15/rads的角亠速度沿顺时针匀速转运,传送带下表面离Qzzc 地面的高度h不变。
如果物体开始沿曲面下滑时距传送带表面的高度为H初速度为零,g取10m/s2.求:(1)当H=0.2m时,物体通过传送带过程中,电动机多消耗的电能。
(2)当H=1.25m时,物体通过传送带后,在传送带上留下的划痕的长度。
传送带模型

传送带模型因物体与传送带间的动摩擦因数、斜面倾角、传送带速度、传送方向、滑块初速度的大小和方向的不同,传送带问题往往存在多种可能,因此对传送带问题做出准确的动力学过程分析是解决此类问题的关键。
1.水平传送带模型 情景1(1) 传送带较短时,一直加速(2) 传送带较长时,可能先加速后匀速 情景2(1)v 0>v 时,若传送带较短则一直减速,若传送带较长则先减速再匀速 (2)v 0<v 时,若传送带较短则一直加速,若传送带较长则先加速再匀速 情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v 0>v 返回时速度为v ,当v 0≤v 返回时速度为v 0 2.倾斜传送带模型 情景1(1) 传送带较短时,一直加速 (2) 传送带较长时,先加速后匀速 情景2(1)当v 0<v ,同情景1 (2)当v 0=v ,一直匀速(3)当v 0>v ,肯定会受到沿斜面向下的滑动摩擦力, ①传送带较短时,以恒定a 匀减速运动; ②传送带较长时,当mgsin θ大于最大静摩擦力时,整个过程先以a 1减速,后以a 2减速,最终以a 2 加速下滑 当mgsin θ小于等于最大静摩擦力时,整个过程先以a 1减速,后以v 匀速 情景3(1) 传送带较短时,以恒定a 匀加速 (2) 传送带较长时,当mgsin θ大于最大静摩擦力时,整个过程先以a 1加速,后以a 2加速 当mgsin θ小于等于最大静摩擦力时,整个过程先以a 1加速,后以v 匀速 情景4(1)若v 0<v ,同情景3 (2)若v 0=v ,当mgsin θ小于等于最大静摩擦力时,匀速运动, 当mgsin θ大于最大静摩擦力时,匀加速运动(3)若v 0>v ,肯定会受到沿斜面向上的滑动摩擦力, 当mgsin θ = μmg cos θ时,一直匀速; 当mgsin θ > μmg cos θ时,一直匀加速当mgsin θ < μmg cos θ时,若传送带较短时,则以恒定a 匀减速运动;若传送带较长时,先匀减速后以速度v 匀速运动v 0≠0情景5开始时滑块肯定会受到沿斜面向上的滑动摩擦力, (1)当mgsin θ = μmg cos θ时,以速度v 0匀速; (2)当mgsin θ > μmg cos θ时,一直匀加速(3)当mgsin θ < μmg cos θ时,传送带较短时,一直匀减速;传送带较长时,滑块还要被传送带传回上端。
专题19 动力学中的“传送带模型” (解析版)

专题19 动力学中的“传送带模型”专题导航目录常考点 动力学中的“传送带模型”分类分析 ............................................................................................................... 1 考点拓展练习 . (9)常考点 动力学中的“传送带模型”分类分析【典例1】如图,一水平的浅色长传送带上放置一质量为m 的煤块(可视为质点) ,煤块与传送带之间的动摩擦因数为μ.初始时,传送带与煤块都是以速度v 作匀速直线运动;现让传送带以加速度a 作匀减速运动,速度减为零后保持静止;又经过一段时间,煤块静止,传送带上留下了一段黑色痕迹,重力加速度大小为g ,则痕迹长度为( )A .22v gμB .22v aC .2222v v g a μ+ D .2222v v g aμ- 【解析】传送带的运动是匀减速直线运动,加速度为a ,减速到零运动的位移为:x 1=22v a,而煤块的运动也是匀减速直线运动,根据牛顿第二定律:=a g μ煤,减速到零运动走过的位移为x 2=22v gμ,由于煤块和皮带是同一方向运动的,所以痕迹的长度即相对位移为:222122v v x x x g aμ∆=-=-,故D 正确,ABC 错误。
【典例2】重物A 放在倾斜的传送带上,它和传送带一直相对静止没有打滑,传送带与水平面的夹角为θ,如图所示,传送带工作时,关于重物受到的摩擦力的大小,下列说法正确的是( )A.重物静止时受到的摩擦力一定小于它斜向上匀速运动时受到的摩擦力B.重物斜向上加速运动时,加速度越大,摩擦力一定越大C.重物斜向下加速运动时,加速度越大,摩擦力一定越大D.重物斜向上匀速运动时,速度越大,摩擦力一定越大【解析】AD.重物静止时,受到的摩擦力大小F f=mg sinθ重物匀速上升时,受到的摩擦力大小仍为mg sinθ,且与速度大小无关,AD错误;B.重物斜向上加速运动时,根据牛顿第二定律,摩擦力F f′=mg sinθ+ma加速度越大,摩擦力越大,B正确;C.重物沿斜面向下加速运动时F f″=mg sinθ-ma或F f″=ma-mg sinθ加速度越大,摩擦力不一定越大,C错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传送带模型
1.模型特征
一个物体以速度v 0(v 0≥0)在另一个匀速运动的物体上运动的力学系统可看做“传送带”模型,如图(a)、(b)、(c)所示。
2.建模指导
传送带模型问题包括水平传送带问题和倾斜传送带问题。
(1)水平传送带问题:求解的关键在于对物体所受的摩擦力进行正确的分析判断。
判断摩擦力时要注意比较物体的运动速度与传送带的速度,也就是分析物体在运动位移x (对地)的过程中速度是否和传送带速度相等。
物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻。
(2)倾斜传送带问题:求解的关键在于认真分析物体与传送带的相对运动情况,从而确定其是否受到滑动摩擦力作用。
如果受到滑动摩擦力作用应进一步确定其大小和方向,然后根据物体的受力情况确定物体的运动情况。
当物体速度与传送带速度相等时,物体所受的摩擦力有可能发生突变。
一、水平放置运行的传送带
1.如图所示,物体A 从滑槽某一高度滑下后又滑上粗糙的水平传送带,传送带静止不动时,A 滑至传送带最右端的速度为v 1,需时间t 1,若传送带逆时针转动,A 滑至传送带最右端的速度为v 2,需时间t 2,则( )
A .1212,v v t t ><
B .1212,v v t t <<
C .1212,v v t t >>
D .1212,v v t t ==
2.如图所示,一水平方向足够长的传送带以恒定的速度v 1沿顺时针方向转动,
传送带右端有一与传送带等高的光滑水平面,一物体以恒定速度v 2沿直线向左
滑向传送带后,经过一段时间又反回光滑水平面,速率为v 2′,则下列说法正确
的是:( )
A .只有v 1= v 2时,才有v 2′= v 1
B . 若v 1 >v 2时, 则v 2′= v 2
C .若v 1 <v 2时, 则v 2′= v 2
D .不管v 2多大,v 2′= v 2.
3.水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查右图为一水平传送带装置示意图,绷紧的传送带A 、B 始终保持v =1m/s 的恒定速率运行;一质量为m =4kg 的行李无初速地放在A 处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.1,AB 间的距离l =2m ,g 取10m /s 2.
(1)求行李刚开始运动时所受的滑动摩擦力大小与加速度大小;
(2)求行李做匀加速直线运动的时间;
(3)如果提高传送带的运行速率,行李就能被较快地传送到B 处.求行李从A 处传送到B 处的最短时间和传送带对应的最小运行速率.
4.一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ.起始时,传送带与煤块都是静止的.现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动.求此黑色痕迹的长度.
5:在民航和火车站可以看到用于对行李进行安全检查的水平传送带。
当旅客把行李放到传送带上时,传送带对行李的滑动摩擦力使行李开始做匀加速运动。
随后它们保持相对静止,行李随传送带一起前进。
设传送带匀速前进的速度为0.25m/s,把质量为5kg的木箱静止放到传送带上,由于滑动摩擦力的作用,木箱以6m/s2的加速度前
进,那么这个木箱放在传送带上后,传送带上将留下一段多长的摩擦痕迹
6.一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB边重合,如图,已知盘与桌布间的动摩擦因数为μl,盘与桌面间的动摩擦因数为μ2。
现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。
若圆盘最后未从桌面掉下,则加
速度a满足的条件是什么?(以g表示重力加速度)
二、倾斜放置运行的传送带
7.如图所示,传送带与地面倾角θ=37°,从AB长度为16m,传送带以10m/s的速率逆时针转动.在传送带上端A无初速度地放一个质量为0.5kg的物体,它与传送带之间的动摩擦因数为0.5.求物体从A 运动到B需时间是多少?(sin37°=0.6,cos37°=0.8)
8.如图所示,传送带两轮A、B的距离L=11 m,皮带以恒定速度v=2 m/s运动,现将一质量为m的物块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,传送带的倾角为α=37°,那么物块m 从A端运到B端所需的时间是多少?(g取10 m/s2,cos37°=0.8)
三、组合类的传送带
9.如图所示的传送皮带,其水平部分AB长s AB=2m,BC与水平面夹角θ=37°,长度s BC=4m,一小物体P 与传送带的动摩擦因数 =0.25,皮带沿A至B方向运行,速率为v=2m/s,若把物体P放在A点处,它将被传送带送到C点,且物体P不脱离皮带,求物体从A点被传送到C点所用的时间.(sin37°=0.6,g=l0m/s2)
10.如图所示为一货物传送货物的传送带abc . 传送带的ab 部分与水平面夹角α=37°,bc 部分与水平面夹角β=53°,ab 部分长度为4.7m ,bc 部分长度为3.5m. 一个质量为m =1kg 的小物体A (可视为质点)与传送带的动摩擦因数μ=0.8. 传送带沿顺时针方向以速率v =1m/s 匀速转动. 若把物体A 轻放到a 处,它将被传送带送到c 处,此过程中物体A 不会脱离传送带.(sin37°=0.6,sin53°=0.8,g =10m/s 2)
求:物体A 从a 处被传送到b 处所用的时间;
11.右图为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A ,B 两端相距3m ,另一台倾斜,传送带与地面的倾角,C, D 两端相距4. 45m ,B, C 相距很近。
水平传送以5m/s 的速度沿顺时针方向转动,现将质量为10kg 的一袋大米无初速度地放在A 段,它随传送带到达B 端后,速度大小不变地传到倾斜送带的C 点,米袋与两传送带间的动摩擦因数均为0. 5, (g 取10m/s 2,sin37˚=0. 6,cos37˚=0. 8)
(1)若CD 部分传送带不运转,求米袋沿传送带在CD 上所能上升的最大距离;
(2)若倾斜部分CD 以4m /s 的速率顺时针方向转动,求米袋从C 运动到D 所用的时间。
βαa b c h A。
