网格作图题
云南中考数学题型专项（六）网格作图题（含答案）
题型专项(六) 网格作图题网格作图题是对图形变换的综合考查，在网格中可以同时考察平移、旋转、轴对称、中心对称等几种图形变换．此类题目属于图形的操作问题，在网格中进行图形变换的操作时，图形的每一个顶点都是关键点，可以将图形的变换操作转化为点的变换操作．此类题目属中档题，复习时注意练习即可．1．(·宁夏)如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2，－1)，B(3，－3)，C(0，－4)．(1)画出△ABC关于原点O成中心对称的△A1B1C1；(2)画出△A1B1C1关于y轴对称的△A2B2C2.解：(1)△A1B1C1如图所示．(2)△A2B2C2如图所示．2．(·昆明二模)在如图所示的方格纸中，每个小正方形的边长都是1，△ABC和△A1B1C1成中心对称．(1)请在图中画出对称中心O；(2)在图中画出将△A1B1C1沿直线DE平移5格得到的△A2B2C2；(3)要使△A2B2C2与△CC1C2重合，需将△A2B2C2绕点C2顺时针旋转，则至少要旋转90度．解：(1)如图，点O即为所求．(2)如图，△A2B2C2即为所求．3．(·昆明西山区一模)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－4，3)，B(－3，1)，C(－1，3)．(1)请按下列要求画图：①将△ABC先向右平移4个单位长度，再向上平移2个单位长度，得到△A1B1C1，画出△A1B1C1；②△A2B2C2与△ABC关于原点O中心对称，画出△A2B2C2；(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称，请直接写出对称中心M点的坐标(2，1)．解：(1)①如图：△A1B1C1即为所求．②如图：△A2B2C2即为所求．4．(·昆明模拟)在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C＝90°，AC＝3，BC＝4.(1)试在图中作出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；(2)若点B的坐标为(－3，5)，试在图中画出直角坐标系，并标出A，C两点的坐标；(3)根据(2)的坐标系作出与△ABC 关于原点对称的图形△A 2B 2C 2，并标出B 2，C 2两点的坐标．解：(1)△AB 1C 1如图所示．(2)如图所示，A(0，1)，C(－3，1)．(3)△A 2B 2C 2如图所示，B 2(3，－5)，C 2(3，－1)．5．(·龙东)如图，在平面直角坐标系中，点A 、B 、C 的坐标分别为(－1，3)、(－4，1)、(－2，1)，先将△ABC 沿一确定方向平移得到△A 1B 1C 1，点B 的对应点B 1的坐标是(1，2)，再将△A 1B 1C 1绕原点O 顺时针旋转90°得到△A 2B 2C 2，点A 1的对应点为点A 2.(1)画出△A 1B 1C 1；(2)画出△A 2B 2C 2；(3)求出在这两次变换过程中，点A 经过点A 1到达点A 2的路径总长．解：(1)如图，△A 1B 1C 1即为所求．(2)如图，△A 2B 2C 2即为所求．(3)OA 1＝42＋42＝42，点A 经过点A 1到达A 2的路径总长为52＋12＋90·π·42180＝26＋22π. 6．(·昆明模拟)如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A(－1，1)，B(－3，1)，C(－1，4)．(1)画出△ABC 关于y 轴对称的△A 1B 1C 1；(2)将△ABC 绕着点B 顺时针旋转90°后得到△A 2BC 2，请在图中画出△A 2BC 2，并求出线段BC 旋转过程中所扫过的面积(结果保留π)．解：(1)如图所示，△A 1B 1C 1即为所求．(2)如图所示，△A 2BC 2即为所示，线段BC 旋转过程中所扫过的面积S ＝90×13π360＝13π4. 7．(·昆明盘龙区二模)如图，△ABC 三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．(1)请画出将△ABC先向左，再向下都平移5个单位长度后得到的△A1B1C1；(2)请画出将△ABC绕O按逆时针方向旋转90°后得到的△A2B2C2；(3)在x轴上求作一点P，使△PAB周长最小，请画出△PAB并直接写出点P的坐标．解：(1)如图，△A1B1C1即为所求．(2)如图，△A2B2C2即为所求．(3)如图，△PAB即为所求，P(2，0)．8．(·云南模拟)图中的小方格都是边长为1的正方形，△ABC的顶点和O点都在正方形的顶点上．(1)以点O为位似中心，在方格图中画出将△ABC放大为原来的2倍得到的△A′B′C′；(2)△A′B′C′绕点B′顺时针旋转90°，画出旋转后得到的△A″B′C″，并求边A′B′在旋转过程中扫过的图形面积．解：(1)如图，△A′B′C′即为所求．(2)如图，△A″B′C″即为所求．S＝90360π(22＋42)＝14π·20＝5π.。
中考数学 中档题突破 专项训练七 网格作图和尺规作图
(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD 于点E，交边BC于点F(要求：尺规作图并保留作图痕迹，不写作法，标 明字母)； 解：(1)如图．
(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明． AE＝CF. 证明：∵四边形ABCD 是矩形，∴AD∥BC， ∴∠EAO＝∠FCO， ∠AEO＝∠CFO. ∵EF为AC的垂直平分线，∴OA＝OC， ∴△AEO≌△CFO ，∴AE＝CF.
3．(2022·无锡)如图，△ABC为锐角三角形．
(1)请在图①中用无刻度的直尺和圆规作图：在AC右上方确定点D ，使 ∠DAC＝∠ACB，且CD⊥AD；(不写作法，保留作图痕迹) 解：如图，点D为所求点．
(2)在(1)的条件下，若∠B＝60°，AB＝2, BC＝3，则四边形ABCD的面 积为________．(如需画草图，请使用试卷中的图②) 过点A作AE⊥BC，垂足为点E， ∵∠B＝60°，∠AEB＝90°， ∴∠BAE＝90°－60°＝30°， ∵AB＝2，
2．如图，在△ABC中，AB＝AC，点P在BC上．
(1)求作：△PCD，使点D在AC上，且△PCD∽△ABP；(要求：尺规作图， 保留作图痕迹，不写作法) 解：如答图， 作出∠APD＝∠ABP，即可得到△PCD∽△ABP.
(2)在(1)的条件下，若∠APC＝2∠ABC，求证：PD∥AB. 证明：如答图， ∵∠APC＝2∠ABC，∠APD＝∠ABC， ∴∠DPC＝∠ABC，∴PD∥AB.
1 ∴△A1B1C1∽△A2B2C2，且相似比为2， ∴S△A1B1C1∶S△A2B2C2＝122＝14.
3．(2022·柳州城中区模拟)如图，在平面直角坐标系中，已知△ABC的 三个顶点坐标分别是A(2，－1)，B(1，－2)，C(3，－3)．
中考数学专题《在网格线中作图》
(1)在图1中,画出线段AB的垂直平分线MN；
(2)在图2中,线段CD∥AB,画出线段CD的中点O.
M
利用轴对称
的性质作图
A
A
N B
利用梯形 四点共线作图
C O D B
知识点
01 利用常用技巧作图 02 利用性质作位置关系 03 利用性质作数量关系 04 按要求构造图形
典例精讲
利用性质作位置关系
知识点二
【例2】(2016·T17)如图,六个完全相同的小长方形拼成一个大长方形,AB
是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求：
1仅用无刻度直尺,2保留必要的画图痕迹.
(1)在图1中画一个45º角,使点A或点B是这个角的顶点,AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
典例精讲
通过计算面积作图
知识点三
【例3】(2014·T17)已知梯形ABCD,请使用无刻度直尺画一个与梯形ABCD
面积相等的图形.
(1)在图1中,画以CD为边的三角形；
(2)在图2中,画以AB为边的平行四边形.
A
D
A
D
F
EB
C
如图1
如图1,△CDE即为所求；
B
E
C
如图2
如图2,□ABEF即为所求.
完成下列作图.
(1)在图1中,作线段AB∥MN； (2)在图2中,作线段CD⊥MN.
A M
M
CC C
A
NB
N
图1 B
D D D 图2
当堂训练
利用性质作位置关系
知识点二
2.如图,在正三角形网格内,A、B、P、Q均为网格格点,仅用无刻度的直尺
2023年中考数学《网格作图》真题及答案解析
2023中考真题抢先练：数学网格作图1.（2023达州18题）如图，网格中每个小正方形的边长均为1，△ABC 的顶点均在小正方形的格点上.（1）将△ABC 向下平移3个单位长度得到△A 1B 1C 1，画出△A 1B 1C 1；（2）将△ABC 绕点C 顺时针旋转90度得到△A 2B 2C 2，画出△A 2B 2C 2；（3）在（2）的运动过程中请计算出△ABC 扫过的面积.第1题图【推荐区域：安徽陕西】【参考答案】解：（1）如解图，△A 1B 1C 1即为所求；（2）如解图，△A 2B 2C 2即为所求；第1题解图（3）由图可得，△ABC 为等腰直角三角形，∴51222=+==BC AB ，AC =101322=+，∴25552121=´´=×=D BC AB S ABC ，∴△A 1B 1C 1在旋转过程中扫过的面积为2ABCACA S S D +扇形290360p ´=+52=52π+52.反比例与一次函数性质综合题2.（2023自贡24题）如图，点A (2，4)在反比例函数xm y =1图象上，一次函数b kx y +=2的图象经过点A ，分别交x 轴，y 轴于点B ，C ，且△OAC 与△OBC 的面积比为2：1.（1）求反比例函数和一次函数的解析式；（2）请直接写出y 1≥y 2时，x 的取值范围.第2题图【推荐区域：安徽江西甘肃】【参考答案】解：（1）将A （2，4）代入x m y =1中得24m =，解得m =8，∴xy 81=，∵C （0，b ），∴12OAC S OC D =·2=b ，∵△OAC 与△OBC 的面积比为2：1，∴b OB OC S OBC 2121=´=D ，解得OB =1，∴B （-1，0）或（1，0），①将A （2，4），B （-1，0）代入b kx y +=2中，得îíì+-=+=，，b k b k 024解得ïîïíì==，，3434b k ∴34342+=x y ；②将A （2，4），B （1，0）代入b kx y +=2中，得îíì+=+=，，b k b k 024解得îíì-==，，44b k ∴442-=x y ；综上可知，一次函数的解析式为34342+=x y 或442-=x y ；（2）当34342+=x y 时，x ≤-3或0＜x ≤2；当442-=x y 时，x ≤-1或0＜x ≤2.解直角三角形的实际应用3.（2023达州19题）莲花湖湿地公园是当地人民喜爱的休闲景区之一，里面的秋千深受孩子们喜爱，如图所示，秋千链子的长度为3m ，当摆角∠BOC 恰为26°时，座板离地面的高度BM 为0.9m ，当摆动至最高位置时，摆角∠AOC 为50°，求座板距地面的最大高度为多少m?(结果精确到0.1m ；参考数据：sin 26°=0.44，cos 26°≈0.9，tan 26°≈0.49，sin 50°≈0.77，cos 50°≈0.64，tan 50°≈1.2)第3题图【推荐区域：安徽江西河南甘肃】【参考答案】解：如解图，过点B 作BD ⊥ON 于点D ，过点A 作AE ⊥ON 于点E ，作AF ⊥MN于点F，第3题解图∴四边形BDNM，AENF均为矩形，∴BM=DN=0.9，AF=EN，在Rt△OBD中，OD=OB·cos26°=3cos26°，∴ON=OD+DN=3cos26°+0.9，在Rt△OAE中，OE=OA·cos50°=3cos50°，∴EN=ON-OE=3cos26°+0.9-3cos50°，∴AF=3cos26°+0.9-3cos50°≈3×0.9+0.9-3×0.64=1.68≈1.7（m），答：座板距地面的最大高度为1.7m.4.（2023重庆A卷24题）为了满足市民的需求，我市在一条小河AB两侧开辟了两条长跑锻炼线路，如图：①A—D—C—B；②A—E—B.经勘测，点B在点A的正东方，点C在点B的正北方10千米处，点D在点C的正西方14千米处，点D在点A的北偏东45°方向，点E在点A的正南方，点E在点B的南偏西60°方向.( 1.41≈1.73)（1）求AD的长度；(结果精确到1千米)（2）由于时间原因，小明决定选择一条较短线路进行锻炼，请计算说明他应该选择线路①还是线路②?第4题图【推荐区域：安徽江西河南甘肃】【参考答案】解：（1）如解图，过点D作DF⊥AB于点F.第4题解图由题意可知，AB∥CD，BC⊥AB，∴四边形BCDF是矩形，且BC=10，CD=14.∴DF=BC=10，在Rt△ADF中，∠DAF=45°，∴AD≈14（千米），答：AD的长度约为14千米；（2）由题意可知，EA⊥AB，∠ABE=90°-60°=30°，∵AF=DF=10，BF=CD=14，∴AB=AF+BF=10+14=24，∴在Rt△ABE中，AE AB BE=2AE线路①：AD+CD+BC≈38.1（千米），线路②：AE+BE41.52（千米），∵38.1＜41.52，∴小明应选择线路①.二次函数的实际应用5.（2023南充23题）某工厂计划从A ，B 两种产品中选择一种生产并销售，每日产销x 件，已知A 产品成本价m 元/件(m 为常数，且4≤m ≤6)，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B 产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y 元，y (元)与每日产销x （件）满足关系式201.080x y +=.（1）若产销A ，B 两种产品的日利润分别为1w 元，2w 元，请分别写出1w ，2w 与x 的函数关系式，并写出x 的取值范围；（2）分别求出产销A ，B 两种产品的最大日利润；(A 产品的最大日利润用含m 的代数式表示)（3）为获得最大日利润，该工厂应该选择产销哪种产品?并说明理由.[利润=(售价一成本)×产销数量一专利费]【推荐区域：安徽河北云南江西】【参考答案】解：（1）根据题意，得30)8(1--=x m w ，0≤x ≤500.)01.080()1220(22x x w +--=80801.02-+-=x x ，0≤x ≤300；（2）∵8-m >0，∴1w 随x 的增大而增大，又0≤x ≤500，∴当x =500时，1w 的值最大，39705001+-=m w 最大.1520)400(01.080801.0222+--=-+-=x x x w .∵-0.01<0，对称轴为直线x =400，当0≤x ≤300时，2w 随x 的增大而增大，∴当x =300时，2w 最大=-0.01×(300-400)2+1 520=1 420（元）.（3）①若最大1w =最大2w ，即-500m +3970=1420，解得m =5.1；②若最大1w >最大2w ，即-500m +3970>1 420，解得m <5.1；③若最大1w <最大2w ，即-500m +3 970<1420，解得m >5.1.又∵4≤m ≤6，∴综上可得，为获得最大日利润：当m =5.1时，选择A ，B 产品产销均可；当4≤m <5.1时，选择A 种产晶产销；当5.1<m ≤6时，选择B 种产品产销.二次函数性质综合题6.（2023遂宁25题）在平面直角坐标系中，O 为坐标原点，抛物线c bx x y ++=241经过点O (0，0)，对称轴过点B (2，0)，直线l 过点C (2，-2)且垂直于y 轴.过点B 的直线1l 交抛物线于点M ，N ，交直线l 于点Q ，其中点M ，Q 在抛物线对称轴的左侧.（1）求抛物线的解析式；（2）如图1，当BM ：MQ =3：5时，求点N 的坐标；（3）如图2，当点Q 恰好在y 轴上时，P 为直线1l 下方的抛物线上一动点，连接PQ ，PO ，其中PO 交1l 于点E ，设△OQE 的面积为1S ，△PQE 的面积为2S ，求12S S 的最大值.第6题图【推荐区域：安徽陕西】【参考答案】解：（1）由题意得0b 2124c =ìïïí-=ï´ïî，，解得01c b =ìí=-î，，∴抛物线的解析式为y =214x -x ；（2）如解图，过点M ，Q 作MD ⊥x 轴，QH ⊥x 轴分别于点D ，H ，第6题解图∴DM ∥HQ ，∴△BDM ∽△BHQ ，∴BM BQ =DM HQ ，∴38=2DM ，∴DM =34，∴点M 的纵坐标为-34，代入y =34x 2-x 中，解得x M =1或x M =3，∵点M 在抛物线对称轴的左侧，∴x M =1，∴点M （1，-34），设直线BM 的解析式为y =kx +b 1，将点M （1，-34）和点B （2，0）代入，得113=402k b k b ì-+ïíï=+î，，解得13=432k b ìïïíï=-ïî，，∴直线BM 的解析式为y =2343-x ，联立2143342y x x y x ì=-ïïíï=-ïî，，解得134x y =ìïí=-ïî，或63x y =ìí=î，，∵点N 在对称轴的右侧，∴点N （6，3）；（3）由题意可知，点Q 的坐标为（0，-2），设点P （m ，14m 2-m ），由题意得直线y OP =（14m -1）x ，直线l 1的解析式为y BQ =x -2，联立1(1)42y m x y x ì=-ïíï=-î，，∴点E 的横坐标为x E =88m -，∴S 1=21OQ ·x E =21×2×m -88=m-88，S 2=21OQ ·(P E x x -）=21×2（m -m-88）=m m m ---8882，∴22188888S m m m S m ---=-=1812-+-m m =1)4812+--m （，∵81-＜0，∴当m =4时，12S S 有最大值，最大值为1，∴12S S 的最大值为1.。
中考数学题型训练网格作图
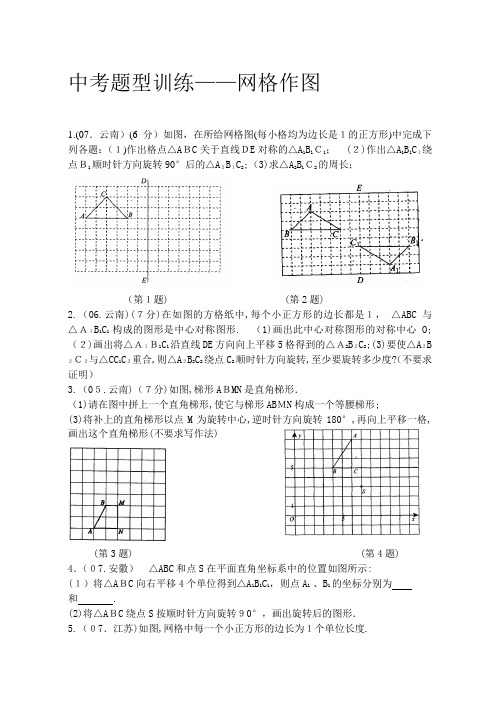
中考题型训练——网格作图1.(07．云南）(6分）如图，在所给网格图(每小格均为边长是１的正方形)中完成下列各题：（１)作出格点△AＢC关于直线ＤE对称的△A1B1Ｃ1； (２)作出△A1B1C１绕点Ｂ1顺时针方向旋转90°后的△A２B１C2;（3)求△A2B1Ｃ2的周长；（第１题) (第2题)2.（06.云南)(７分)在如图的方格纸中,每个小正方形的边长都是１，△ABC与△Ａ１B1C1构成的图形是中心对称图形. （1)画出此中心对称图形的对称中心O; （２)画出将△Ａ１Ｂ1C1沿直线DE方向向上平移5格得到的△Ａ2B２C2;(3)要使△A２B ２Ｃ２与△CC1C２重合,则△A２B2C2绕点C2顺时针方向旋转,至少要旋转多少度?（不要求证明）3.（0５.云南)（７分)如图,梯形AＢMN是直角梯形．（1)请在图中拼上一个直角梯形,使它与梯形ABＭN构成一个等腰梯形;(3)将补上的直角梯形以点M为旋转中心,逆时针方向旋转180°,再向上平移一格,画出这个直角梯形(不要求写作法)(第3题) (第4题) 4．（０7.安徽）△ABC和点S在平面直角坐标系中的位置如图所示:(１）将△AＢC向右平移4个单位得到△A1B1C1，则点A1 、B1的坐标分别为和 .(2)将△AＢC绕点S按顺时针方向旋转９0°，画出旋转后的图形．5.（０7．江苏)如图,网格中每一个小正方形的边长为１个单位长度.(1)请在所给的网格内画出以线段AB,ＢC为边的菱形ABＣD；(2)填空:菱形ABCD的面积等于．(第5题）(第6题）6．（07.福州)如图的方格纸中,每个小正方形的边长都为1个单位的正方形，在建立平面直角坐标系后, △ABＣ的顶点均在格点上,点Ｃ的坐标为(４,-1）.(1)把△ABC向上平移5个单位后得到对应的△A１B1C1,画出△A1B1Ｃ1,并写出点C１的坐标;（２）以原点O为对称中心,再画出与△A１B1Ｃ１关于原点Ｏ对称的△Ａ2B2C2，并写出点Ｃ2的坐标.7.（０7.哈尔滨)△ABC在平面直角坐标系中的位置如图所示．（1)作出与△ABＣ关于y轴对称的△A１Ｂ1C;(２）将△ABＣ向下平移３个单位长度,画出平移后的△Ａ2Ｂ2C2.(第７题) (第8题)８.（０７.辽宁）如图, 在平面直角坐标系中,图错误!与图错误!关于点P成中心对称.(1)画出对称中心P，并写出点Ｐ的坐标;(2)将图形＼o＼ac（○,2)向下平移4个单位,画出平移后的图形错误!,并判断图形错误!与图形错误!的位置关系.（直接写出结果)９.（０７.安徽)如图，在直角坐标系中△ＡBC的A、B、Ｃ三点坐标为Ａ(7，1）、B(8，2）、C(９,0)．(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形(要求与△ＡＢＣ同在P点一侧);（2)求线段BC的对应线段Ｂ′Ｃ′所在直线的表达式.(第９题） (第10题）10．(０７.长沙)如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作: (1）作出关于直线AB的轴对称图形；（2）将你画出的部分连同原图形绕点O逆时针旋转90°;(3)发挥你的想象,给得到的图案适当涂上阴影,让图案变得更加美丽．1１.(０7．海南)在如图的方格纸中,△ABC的顶点坐标分别为A（－２，5)、Ｂ(-４，１)和C（-1,3）.（1)作出△ＡＢC关于x轴对称的△A1B1C1，并写出点Ａ、B、Ｃ的对称点A1、B1、C1的坐标；（２)作出△ABＣ关于原点Ｏ对称的△A2Ｂ2C２,并写出点A、B、Ｃ的对称点A2、B2、C2的坐标;（３）试判断:△Ａ1Ｂ1Ｃ１与△Ａ2B2Ｃ2是否关于y轴对称（只需写出判断结果）(第11题) （第12题）１2．(07.青海)如图所示,图错误!和图错误!中的每个小正方形的边长都为1个单位长度．(1）将图错误!中的格点△AＢC（顶点都在网格线交点的三角形叫格点三角形）向在平移2个单位长度得到△A1B1C1,请你在图中画出△A1Ｂ1C1;(2)在图错误!中画一个与格点△AＢC相似的格点△A２B2C2，且△A2B2Ｃ２与△ABC的相似比为2：１．１3.（07．广西)如图，在正方形网格中,△ＡＢC的三个顶点Ａ、B、C均在格点上，将△ABC向右平移5格,得到△Ａ1Ｂ１Ｃ1,再将△A1B１Ｃ1绕点B1按顺时针方向旋转90°，得到△A２Ｂ２C2.（1)请在网格中画出△A1Ｂ1Ｃ1和△A2Ｂ２C2（不要求写画法）(2)画出△Ａ１B1C1和△A2B2Ｃ２后,填空：∠C1B1Ｃ2= 度，∠A2＝度.（第1３题）１４.(0６.成都)如图,在平面直角坐标系中,点B的坐标为（-１，-１).(1）把△ABC向左平移8格后得到△Ａ1B1C１,画出△A１B1Ｃ1并写出点Ｂ１的坐标; (２）把△ABＣ绕点C按顺时针方向旋转９0°后得到△Ａ２B２C，画出△A2Ｂ2Ｃ并写出点B2的坐标；(3）把△AＢC以点Ａ为位似中心放大，使放大前后对应边长的比为1:2,画出△AB3C3.(第1４题）１5.(0６.广东)如图，图中的小正方形是边长为1的正方形,△AＢC与是关于O为位似中心的位似图形,它们的顶点都在小正方形的顶点上．(1)画出位似中心点O;(2)求出△ABC与的位似比；（３）以点Ｏ为位似中心,再画一个△A1B1C1，使它与△ABＣ的位似比为1.5；。
中考数学专题复习(三)网格作图题(含答案)
专题复习(三)网格作图题1．拟)如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点四边形ABCD(顶点是网格线的交点)，按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心，将四边形ABCD顺时针旋转90°，得到四边形AB1C1D1；(2)以A为位似中心，将四边形ABCD作位似变换，且放大到原来的两倍，得到四边形AB2C2D2.解：(1)如图，四边形AB1C1D1为所作．(2)如图，四边形AB2C2D2为所作．2．二模)如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为(1，0)．(1)画出△ABC关于x轴对称的△A1B1C1，写出B1点的坐标；(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2，写出B2点的坐标．解：(1)如图所示，△A1B1C1即为△ABC关于x轴对称的图形，B1点的坐标是(1，0)．(2)如图所示，△A2B2C2即为△ABC绕原点O按逆时针旋转90°的三角形，B2点的坐标是(0，1)．3．模)如图，已知A(2，3)，B(1，1)，C(4，1)是平面直角坐标系中的三点．(1)请画出△ABC关于y轴对称的△A1B1C1；(2)画出△A1B1C1向下平移3个单位得到的△A2B2C2；(3)若△ABC中有一点P坐标为(x，y)，请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标．解：(1)如图所示，△A1B1C1即为所求．(2)如图所示，△A2B2C2即为所求．(3)根据题意，可得P的对应点P2的坐标为(－x，y－3)．4．拟)如图，在9×7的小正方形网格中，△ABC的顶点A，B，C在网格的格点上．将△ABC向左平移3个单位，再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转：第1次，将△ABC绕点B顺时针旋转90°得到△A1BC1；第2次，将△A1BC1绕点A1顺时针旋转90°得到△A1B1C2；第3次，将△A1B1C2绕点C2顺时针旋转90°得到△A2B2C2；第4次，将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3，依次旋转下去．(1)在网格中画出△A′B′C′和△A2B2C2；(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.解：(1)△A′B′C′和△A2B2C2的图象如图所示.(2)通过画图可知，△ABC至少在第8次旋转后得到△A′B′C′.5.如图，△ABC的三个顶点和点O都在正方形网格的格点上，每个小正方形的边长都为1.(1)将△ABC先向右平移4个单位，再向上平移2个单位得到△A1B1C1，请画出△A1B1C1；(2)请画出△A2B2C2，使△A2B2C2和△ABC关于点O成中心对称；(3)在(1)、(2)中所得到的△A1B1C1与△A2B2C2成轴对称吗？若成轴对称，请画出对称轴；若不成轴对称，请说明理由．解：(1)如图所示，△A1B1C1，即为所求．(2)如图所示，△A2B2C2，即为所求．(3)如图所示，△A1B1C1与△A2B2C2成轴对称，直线a，b即为所求．6．级二模)如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC 的顶点A ，B ，C 在小正方形的顶点上．将△ABC 向下平移2个单位得到△A 1B 1C 1，然后将△A 1B 1C 1绕点C 1顺时针旋转90°得到△A 2B 2C 1.(1)在网格中画出△A 1B 1C 1和△A 2B 2C 1；(2)计算线段AC 在变换到A 2C 1的过程中扫过区域的面积．(重叠部分不重复计算)解：(1)如图，△A 1B 1C 1和△A 2B 2C 1为所作．(2)线段AC 在变换到A 2C 1的过程中扫过区域的面积S ＝2×2＋90·π·（22）2360＝4＋2π.7．如图，△ABC 三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．(1)请画出将△ABC 向左平移4个单位长度后得到的图形△A 1B 1C 1；(2)请画出△ABC 关于原点O 成中心对称的图形△A 2B 2C 2；(3)在x 轴上找一点P ，使PA ＋PB 的值最小，请直接写出点P 的坐标．解：(1)如图所示．(2)如图所示．(3)找出A 关于x 轴的对称点A′(1，－1)，连接BA′，与x 轴交点即为P.如图所示，点P 坐标为(2，0)．8．模拟)如图，已知△ABC 的三个顶点的坐标分别为A(3，3)，B(－1，0)，C(4，0)．(1)经过平移，可使△ABC 的顶点A 与坐标原点O 重合，请直接写出此时点C 的对应点C 1坐标；(不必画出平移后的三角形)(2)将△ABC 绕点B 逆时针旋转90°，得到△A′BC′，画出△A′BC′并写出A′点的坐标；(3)以点A 为位似中心放大△ABC ，得到△AB 2C 2，使放大前后的面积之比为1∶4，请你在网格内画出△AB 2C 2.解：(1)∵经过平移，可使△ABC的顶点A与坐标原点O重合，∴A点向下平移3个单位再向左平移3个单位，故C1坐标为(1，－3)．(2)如图所示，△A′BC′即为所求，A′点的坐标为(－4，4)．(3)如图所示，△AB2C2即为所示．。
专题02网格类作图题中考题型训练(原卷版)
专题2 网格类作图题中考题型训练1．（2022•荆州）如图，在10×10的正方形网格中，小正方形的顶点称为格点，顶点均在格点上的图形称为格点图形，图中△ABC为格点三角形．请按要求作图，不需证明．（1）在图1中，作出与△ABC全等的所有格点三角形，要求所作格点三角形与△ABC有一条公共边，且不与△ABC重叠；（2）在图2中，作出以BC为对角线的所有格点菱形．2．（2022•宁波）图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段AB的端点均在格点上，分别按要求画出图形．（1）在图1中画出等腰三角形ABC，且点C在格点上．（画出一个即可）（2）在图2中画出以AB为边的菱形ABDE，且点D，E均在格点上．3．（2022•丽水）如图，在6×6的方格纸中，点A，B，C均在格点上，试按要求画出相应格点图形．（1）如图1，作一条线段，使它是AB向右平移一格后的图形；（2）如图2，作一个轴对称图形，使AB和AC是它的两条边；（3）如图3，作一个与△ABC相似的三角形，相似比不等于1．4．（2022•衢州）如图，在4×4的方格纸中，点A，B在格点上．请按要求画出格点线段（线段的端点在格点上），并写出结论．（1）在图1中画一条线段垂直AB．（2）在图2中画一条线段平分AB．5．（2022•长春）图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．（1）网格中△ABC的形状是；（2）在图①中确定一点D，连结DB、DC，使△DBC与△ABC全等；（3）在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA；（4）在图③中△ABC的边AB上确定一点P，在边BC上确定一点Q，连结PQ，使△PBQ∽△ABC，且相似比为1：2．6．（2022•湖北）已知四边形ABCD为矩形，点E是边AD的中点，请仅用无刻度的直尺完成下列作图，不写作法，保留作图痕迹．（1）在图1中作出矩形ABCD的对称轴m，使m∥AB；（2）在图2中作出矩形ABCD的对称轴n，使n∥AD．7．（2022•江西）如图是4×4的正方形网格，请仅用无刻度的直尺按要求完成以下作图（保留作图痕迹）．（1）在图1中作∠ABC的角平分线；（2）在图2中过点C作一条直线l，使点A，B到直线l的距离相等．8．（2023•锡山区校级模拟）如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上．（Ⅰ）线段AC的长等于；（Ⅱ）以AB为直径的半圆的圆心为O，在线段AB上有一点P，满足AP＝AC．请用无刻度的直尺，在如图所示的网格中，画出点P．9．（2023•鄞州区校级一模）如图，在6×6的方格纸中，每个小正方形的边长为1，点A，B均在格点上，在图1和图2中分别画出一个以点A，B为顶点且另两个顶点均在格点上的正方形，并分别求出其周长．10．（2023•衢州模拟）如图在7×7的方格中，有两个格点A、B．请用无刻度的直尺按要求画图．（1）在图1中画线段AB中点C；（2）在图2中在线段AB上找一点D，使AD：DB＝1：2．11．（2023•宁波模拟）作图题（1）填空：如果长方形的长为3，宽为2，那么对角线的长为．（2）如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点（端点），分别按下列要求画图（不要求写画法和证明，但要标注顶点）．①在图1中，画一个面积为4的菱形，且邻边不垂直．②在图2中，画平行四边形ABCD，使∠A＝45°，且面积为6．12．（2023•杨浦区一模）新定义：由边长为1的小正方形构成的网格图形中，每个小正方形的顶点称为格点．如图，已知在5×5的网格图形中，△ABC的顶点A、B、C都在格点上．请按要求完成下列问题：（1）S△ABC＝；sin∠ABC＝；（2）请仅用无刻度的直尺在线段AB上求作一点P，使S△ACP＝S△ABC．（不要求写作法，但保留作图痕迹，写出结论）13．（2023•武汉模拟）如图是由小正方形组成的7×6网格，每个小正方形的顶点叫做格点．仅用无刻度的直尺在给定网格中完成画图．（1）在图（1）中，A，B，C三点是格点，画经过这三点的圆的圆心O，并在该圆上画点D，使AD＝BC；（2）在图（2）中，A，E，F三点是格点，⊙I经过点A．先过点F画AE的平行线交⊙I于M，N两点，再画弦MN的中点G．14．（2023•乌鲁木齐一模）请仅用无刻度的直尺在网格中完成下列作图，保留作图痕迹，不写作法．（1）图①是由边长为1的小等边三角形构成的网格，△ABC为格点三角形．在图①中，画出△ABC中AB边上的中线CM；（2）如图②，四边形ABCD中，AD∥BC，∠A＝∠D，画出BC边的垂直平分线n．15．（2023•靖江市校级模拟）如图是由小正方形组成的9×7网格，每个小正方形的顶点叫做格点，A，B，C三个格点都在圆上．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．（1）画出该圆的圆心O，并画出劣弧的中点D；（2）画出格点E，使EA为⊙O的一条切线，并画出过点E的另一条切线EF，切点为F．16．（2023•九台区模拟）图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C均在格点上．只用无刻度的直尺，在给定的网格中，按照要求作图（保留作图痕迹）．（1）在图①中作△ABC的中线BD．（2）在图②中作△ABC的高BE．（3）在图③中作△ABC的角平分线BF．17．（2023•迁安市模拟）如图是由边长为1的小正方形组成的网格，△ABC的顶点均在格点上．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示，画图结果用实线表示．（1）在图（1）中画△ABC的高CH；（2）在图（1）的线段AC上画一点D，使得S△ABD：S△CBD＝2：3；（3）在图（2）中C点的右侧画一点F，使∠FCA＝∠BCA且CF＝2．18．（2022•碧江区校级一模）操作理解，解答问题．（1）如图1：已知△ABC，AB＝AC，直线CD∥AB；①完成作图：以点A为圆心，AB长为半径画弧，交直线CD于点P，连接PB．②试判断①中∠ABP与∠BAC的数量关系，并证明你的结论．（2）如图2：已知△ABC是格点三角形，点C在直线n上，且n∥AB；在直线n上画出点P，连接PB，使得∠PBA＝∠CAB．（不用尺规作图）19．（2022•丽水模拟）图1，图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．（1）在图1中画出一个以AC为底边的等腰△ABC，使点B落在格点上．（2）在图2中画出一个以AC为对角线且面积为6的格点矩形ABCD（顶点均在格点上）．20．（2022•婺城区校级模拟）如图，在4×4的方格中，点A，B，C为格点，利用无刻度的直尺画出满足以下条件的图形（保留必要的辅助线）．（1）在图1中画△ABC的中线BE．（2）在图2中标注△ABC的外心O并画出其外接圆的切线CP．21．（2022•海陵区校级三模）如图（1）（2），在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均落在格点上，以AB为直径的半圆的圆心为O，请用无刻度的直尺，在如图（1）图（2）所示的网格中，在半圆O上画出点P，连接AP，使AP平分∠CAB．22．（2022•吉安模拟）如图，在正方形网格中，△ABC的顶点在格点（网格线的交点）上，请仅用无刻度直尺完成以下作图．（保留作图痕迹）（1）在图1中作△ABC的重心．（2）在图2中作∠AGB＝∠ACB，且G是格点．23．（2022•绿园区校级模拟）如图①，②，③中每个小正方形的边长均为1．△ABC的顶点A，B均落在小正方形的顶点上，点C在小正方形的边上，以AC为直径的半圆的圆心为O．请用无刻度的直尺按要求画图．（1）如图①，在半圆上确定点D，使OD∥AB．（2）如图②，在线段AB的延长线上确定点E，使AE＝AC．（3）如图③，在线段AC上确定点F，使AF＝AB．24．（2022•南关区校级模拟）图①、图②、图③均是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，ABC的顶点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求作图．（不写作法，保留画图痕迹）（1）在图①中，在BC上画一点D，使S△ABD＝S△ACD．（2）在图②中，在BC上画一点E，使S△ABE：S△ACE＝2：3．（3）在图③中，在ABC内画一点F，使S△ACF：S△ABF：S△BCF＝2：3：3.25．（2022•长春模拟）图①、图②分别是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的格点上，请在图①、图②中各取一点（点C必须在小正方形的格点上），使以A、B、C为顶点的三角形分别满足下列要求．（1）在图①中画一个△ABC，使∠ACB＝90°，面积为5；（2）在图②中画一个△ABC，使BA＝BC，∠ABC为钝角，并求△ABC的周长．26．（2022•二道区校级二模）图①、图②、图③均是6×6的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段AB、EF、MN的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求画图．（1）在图①中，画∠ADB＝45°；（2）在图②中，画∠APB＝45°，且点P在线段EF上；（3）在图③中，画∠AQB＝45°，且点Q在线段MN上.27．（2022•香坊区校级三模）如图1、2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．（1）在图1中画出以AC为底边的等腰直角三角形ABC，点B在小正方顶点上；（2）在图2中画出以AC为腰的等腰三角形ACD，点D在小正方形的顶点上，且△ACD的面积为8，并直接写出tan A的值．28．（2022•瑞安市校级三模）如图是由边长为1的小正六边形构成的网格图，网格上的点称为格点．已知格点线段AB，利用网格图，仅用无刻度的直尺来完成下面几何作图．（1）请在图①中作一个格点等腰三角形△ABC；（2）请在图②在线段AB上求作点P，使得AP：BP＝3：4．（要求：不写作法但保留作图痕迹）29．（2022•江夏区模拟）用无刻度直尺作图：（1）如图1，在AB上作点E，使∠ACE＝45°；（2）如图1，点F为AC与网格的交点，在AB上作点D，使∠ADF＝∠ACB；（3）如图2，在AB上作点N，使＝．（4）如图2，在AB上作点M，使∠ACM＝∠ABC.30．（2022•阿城区模拟）如图，在每个小正方形的边长均为1的方格纸中，线段AB和线段DE，点A、B、D、E均在小正方形的顶点上．（1）在方格纸中画出以AB为底边的等腰三角形ABC，使△ABC的面积为10，点C在小正方形的顶点上，直接写出tan∠ABC的值；（2）在方格纸中画出钝角三角形DEF，使∠DEF＝45°，点F在小正方形的顶点上．31．（2022•长春模拟）图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求作图，所画图形的顶点均在格点上．（1）在图①中，画等腰三角形ABC，使其面积为3．（2）在图②中，画等腰直角三角形ABD，使其面积为5．（3）在图③中，画平行四边形ABEF，使其面积为9．32．（2022•朝阳区校级模拟）如图在8×8的网格中，每个小正方形的顶点叫做格点．四边形ABCD的顶点在格点上，用无刻度的直尺在网格中完成下列画图，保留必要的作图痕迹，不要求说明理由．（1）如图1，过点A作线段AF，使AF∥DC，且AF＝DC．（2）如图2，在四边形ABCD边上求作一点E，使点E与四边形ABCD某一顶点连线，能把该四边形分成的两部分恰好拼成一个无缝隙、不重叠的三角形．（画一个即可）（3）如图3，在边AB上求作一点G，使∠AGD＝∠BGC．。
中考数学 中档题突破 专项训练一 网格作图题 类型三：平移、对称在网格中的作图
1.(2022·蚌埠模拟)如图，在每个小正方形的边长为 1 个单位长度的网 格中，点 A，B，C 均是格点(网格线的交点)．
(1)在图中将△ABC 平移得到△A′B′C′，使得点 B 的对应点为点 C，作 出平移后的图形△A′B′C′； (2)用无刻度直尺在图中的线段 AB 上找一点 P，使∠ACP＝∠APC. 解：(1)如图，△A′B′C′即为所求．
(3)求出△A2B2C2 的面积．
解：(3)△A2B2C2 的面积为
1
1
1
3×4－2×1×4－2×1×3＝－2×2×3＝5.5.
(2)如图，点 P 即为所求．
2．(2022·福田区模拟)线段 AB 在平面直角坐标系中的位置如图所示， 其中每个小正方形的边长为 1 个单位长度．
(1)将线段 AB 向左平移 6 个单位长度，作出平移后的线段 A1B1； (2)再将线段 AB 绕点(2，0)顺时针旋转 180°后得到线段 A2B2； 解：(1)如图，线段 A1B1 为所求． (2)如图，线段 A2B2 为所求．
4．在如图所示的正方形网格中，每个小正方形的边长均为 1 个单位长度， △ABC 的三个顶点都在格点上．
(1)在网格中画出△ABC 向下平移 3 个单位长度得到的△A1B1C1； (2)在网格中画出△ABC 关于直线 m 对称的△A2B2C2； 解：(1)如图，△A1B1C1 即为所求．
(2)如图，△A2B2C2 即为所求．
(3)观察线段 A1B1 和线段 A2B2，它们是否关于某点成中心对称？若是，请 写出对称)．
3．如图，在边长为 1 个单位长度的小正方形组成的 12×12 网格中，给 出了以格点(网格线的交点)为端点的线段 AB.
2022年中考数学人教版一轮复习课件：八、解答题专练——网格作图
解：(1)如图①中，△ABC 即为所求(答案不唯一)．
解：(2)如图②中，四边形 ABDE 即为所求．
5．(2021·长春)图①、图②、图③均是 4×4 的正方形网格，每个 小正方形的边长均为 1，每个小正方形的顶点称为格点，点 A， B，C 均为格点，只用无刻度的直尺，分别在给定的网格中找 一格点 M，按下列要求作图：
(1)在图①中，连结 MA，MB，使 MA＝MB； (2)在图②中，连结 MA，MB，MC，使 MA＝MB＝MC； (3)在图③中，连结 MA，MC，使∠AMC＝2∠ABC.
解：(1)(2)(3)如图．
6．(2021·绥化)如图，在网格中，每个小正方形的边长均为 1 个 单位长度，把小正方形的顶点叫做格点，O 为平面直角坐标系 的原点，矩形 OABC 的 4 个顶点均在格点上，连接对角线 OB.
八、解答题专练——网格作图
1．(2021·深圳)如图，在正方形网格中，每个小正方形的边长为 1 个单位． (1)过直线 m 作四边形 ABCD 的对称图形； (2)求四边形 ABCD 的面积．
解：(1)如图所示，四边形积＝S△ABD＋S△BCD
解：(1)如图①，四边形 ABCD 即为所求(答案不唯一)．
解：(2)如图②，四边形 AEBF 即为所求．
3．(2021·丽水)如图，在 5×5 的方格纸中，线段 AB 的端点均在格 点上，请按要求画图．
(1)如图①，画出一条线段 AC，使 AC＝AB，C 在格点上； (2)如图②，画出一条线段 EF，使 EF，AB 互相平分，E，F 均在格点上； (3)如图③，以 A，B 为顶点画出一个四边形，使其是中心对 称图形，且顶点均在格点上．
2021年中考数学复习重点题型(2)——网格作图
重点题型(2)——网格作图杭州温州宁波绍兴嘉兴、舟山湖州台州金华丽水衢州2019年第20题第20题第20题第20题第19题8分8分8分8分6分2020年第20题第18题第19题8分8分6分点分别按下列要求画三角形．(1)在图①中，画一个直角三角形，使它的三边长都是有理数；(2)在图②中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数；(3)在图③中，画一个直角三角形，使它的三边长都是无理数．解：(1)如图①中，△ABC即为所求．(2)如图②中，△ABC即为所求．(3)△ABC即为所求．2．(温州一模)如图，点A，B，C是5×5的方格纸中的三个格点，按下列要求作出格点四边形(顶点在格点上).(1)在图1中画出一个以A，C为顶点的菱形(非正方形)，使点B在该图形内部(不包括在边界上).(2)在图2中画出一个以A，C为顶点的平行四边形，使该图形的一边所在直线与AB夹角为45°.解：(1)如图1，即为以A，C为顶点的菱形；(2)如图2，即为以A，C为顶点的平行四边形．3．在6×6的方格纸中，点A，B，C都在格点上，按要求画图：(1)在图1中找一个格点D，使以点A，B，C，D为顶点的四边形是平行四边形．(2)在图2中仅用无刻度的直尺，把线段AB三等分(保留画图痕迹，不写画法).解：(1)由勾股定理得：CD＝AB＝CD′＝5，BD＝AC＝BD′′＝13，AD′＝BC＝AD′′＝10；画出图形如图1所示；(2)如图2所示．4．如图，在7×6的方格中，△ABC的顶点均在格点上．试按要求画出线段EF(E，F 均为格点)，各画出一条即可．解：①如图：从图中可得到AC边的中点在格点上设为E，过E作AB的平行线即可在格点上找到F，则EF平分BC；②EC＝5，EF＝5，FC＝10，借助勾股定理确定F 点，则EF⊥AC；③借助圆规作AB的垂直平分线即可；5．(2020·吉林)图①、图②、图③都是3×3的正方形网格，每个小正方形的顶点称为格点．A，B，C均为格点．在给定的网格中，按下列要求画图：(1)在图①中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M，N为格点．(2)在图②中，画一条不与AC重合的线段PQ，使PQ与AC关于某条直线对称，且P，Q为格点．(3)在图③中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D，E，F为格点．解：(1)如图①，MN即为所求；(2)如图②，PQ即为所求；(3)如图③，△DEF即为所求．。
提分冲刺预测07网格作图题(5种题型)(原卷版)
提分冲刺预测07网格作图题（5种题型）【安徽十年真题考点及分值细目表】网格作图题（10年10考）题型1：作图—平移变换题型2：作图-旋转变换题型3：作图-位似变换题型4：作图-轴对称变换题型5：作图—相似变换题型1：作图-平移变换1．（2019•安徽）如图，在边长为1个单位长度的小正方形组成的12×12的网格中，给出了以格点（网格线的交点）为端点的线段AB．（1）将线段AB向右平移5个单位，再向上平移3个单位得到线段CD，请画出线段CD．（2）以线段CD为一边，作一个菱形CDEF，且点E，F也为格点．（作出一个菱形即可）2．（2016•安徽）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．（1）试在图中标出点D，并画出该四边形的另两条边；（2）将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．题型2：作图-旋转变换3．（2022•安徽）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．（1）将△ABC向上平移6个单位，再向右平移2个单位，得到△A1B1C1，请画出△A1B1C1；（2）以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到△A2B2C2，请画出△A2B2C2．4．（2021•安徽）如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点（网格线的交点）上．（1）将△ABC向右平移5个单位得到△A1B1C1，画出△A1B1C1；（2）将（1）中的△A1B1C1绕点C1逆时针旋转90°得到△A2B2C1，画出△A2B2C1．5．（2020•安徽）如图，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点（网格线的交点）为端点的线段AB，线段MN在网格线上．（1）画出线段AB关于线段MN所在直线对称的线段A1B1（点A1，B1分别为A，B的对应点）；（2）将线段B1A1绕点B1顺时针旋转90°得到线段B1A2，画出线段B1A2．6．（2013•安徽）如图，已知A（﹣3，﹣3），B（﹣2，﹣1），C（﹣1，﹣2）是直角坐标平面上三点．（1）请画出△ABC关于原点O对称的△A1B1C1；（2）请写出点B关于y轴对称的点B2的坐标，若将点B2向上平移h个单位，使其落在△A1B1C1内部，指出h的取值范围．7．（2023•合肥二模）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点式网格线的交点）．A（0，1），B（3，3），C（1，3）．（1）先将△ABC竖直向下平移5个单位，再水平向右平移2个单位得到△A1B1C1，请画出△A1B1C1；（2）将△ABC绕A点逆时针旋转90°，得到△AB2C2，请画出△AB2C2．8．（2023•怀远县校级二模）如图所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：（1）分别写出点A、B两点的坐标并作出△ABC以原点为旋转中心逆时针旋转180°的△A1B1C1；（2）作出点C关于x轴的对称点P．若点P向右平移x个单位长度后落在△A1B1C1的内部，请直接写出x的取值范围．9．（2023•亳州二模）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣1，1），B（﹣4，2），C（﹣3，3）．（1）将△ABC先向下平移2个单位长度，再向右平移5个单位长度得到△A1B1C1，画出△A1B1C1；（2）将△ABC绕点A按顺时针方向旋转90°得到△A2B2C2，画出△A2B2C2．10．（2023•合肥模拟）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点），直线l也经过格点．（1）画出△ABC关于直线l对称的△A′B′C′；（2）将线段AB绕点A′顺时针旋转90°得到线段DE，画出线段DE．11．（2023•明光市一模）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．（1）请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1；（2）请画出△ABC关于原点O成中心对称的图形△A2B2C2．12．（2023•蜀山区校级一模）如图，在边长为1个单位长度的正方形网格中，给出了以格点（网格线的交点）为顶点的△ABC和过点A的直线l．（1）画出△ABC关于直线l对称的△ADE，使点B与D，C与E为对称点．（2）以D为旋转中心，将△ADE顺时针旋转90°得到△GFD，使点E与F，A与G为对称点，画出△GFD，写出由△ABC通过一种变换得到△GFD的方法．13．（2023•蚌山区校级二模）如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点（网格线的交点）上．已知△ABC是格点△ABD的一部分，且△ABD是轴对称图形．（1）在图中画出△ABD；（2）将△BCD绕点A逆时针旋转90°，得到△B′C′D′，画出△B′C′D′．14．（2023•合肥二模）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，1），B（4，1），C（5，3）．（1）请画出△ABC关于x轴对称的△A1B1C1，点A、B、C分别对应A1、B1、C1；（2）将△ABC以O为旋转中心，顺时针旋转90°，点A、B、C分别对应A2、B2、C2，请画出旋转后的图形△A2B2C2；（3）直接画出△A1B1C1与△A2B2C2关于直线对称的对称轴l．15．（2023•六安三模）如图，在10×10的正方形网格中，小正方形的顶点称为格点，顶点均在格点上的图形称为格点图形，图中△ABC为格点三角形．（1）在图中作出点C关于直线AB对称的点C'；（2）以点C为旋转中心，作出将△ABC顺时针旋转90°后得到的△A1B1C，其中点A与点A1对应，点B与点B1对应．题型3：作图-位似变换16．（2018•安徽）如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O，A，B均为网格线的交点．（1）在给定的网格中，以点O为位似中心，将线段AB放大为原来的2倍，得到线段A1B1（点A，B的对应点分别为A1，B1），画出线段A1B1；（2）将线段A1B1绕点B1逆时针旋转90°得到线段A2B1，画出线段A2B1；（3）以A，A1，B1，A2为顶点的四边形AA1B1A2的面积是20个平方单位．17．（2023•利辛县模拟）已知：△ABC三个顶点的坐标分别为A（2，2），B（4，1），C（1，5）．（1）以点O为位似中心，在第一象限将△ABC放大为原来的2倍，得到△A1B1C1，请在网格中画出△A1B1C1；（2）若点P（x，y）是△ABC内任意一点，点P在△A1B1C1内的对应点为P1，则点P1的坐标为（2x，2y）；（3）请用无刻度直尺将线段AB三等分．题型4：作图-轴对称变换18．（2017•安徽）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF（顶点为网格线的交点），以及过格点的直线l．（1）将△ABC向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形．（2）画出△DEF关于直线l对称的三角形．（3）填空：∠C+∠E＝45°．19．（2015•安徽）如图，在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）．（1）请画出△ABC关于直线l对称的△A1B1C1；（2）将线段AC向左平移3个单位，再向下平移5个单位，画出平移得到的线段A2C2，并以它为一边作一个格点△A2B2C2，使A2B2＝C2B2．20．（2023•合肥模拟）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．（1）画出△ABC以AC为对称轴的对称图形△AB1C．（2）作出△ABC外接圆的圆心O，并求出AB弦所对的劣弧弧长．21．（2023•安徽模拟）如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC在平面直角坐标系中的位置如图所示．（1）将△ABC向上平移3个单位后，再向右平移2个单位得到△A1B1C1，再作△A1B1C1关于x轴对称的△A2B2C2，请画出△A2B2C2并直接写出点A2的坐标．（2）则△A2B2C2的周长为．五．作图-相似变换（共1小题）22．（2014•安徽）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．（1）将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；（2）请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相似比不为1．。
中考试题汇编2022年网格作图(解析版)
【小问2详解】
如图，
【点睛】本题考查了作图，轴对称变换，平行四边形的性质，勾股定理等知识，准确画出图形是解题的关键．
9．（2022温州中考）（8分）如图，在 的方格纸中，已知格点 ，请按要求画格点图形（顶点均在格点上）．
（1）在图1中画一个锐角三角形，使 为其中一边的中点，再画出该三角形向右平移2个单位后的图形．
【小问1详解】
∵
∴ ,
∴ 是直角三角形，
故答案为：直角三角形；
【小问2详解】
如图，点D即为所求作，使 与 全等：
【小问3详解】
如图所示，点E即为所作，且使 ：
【问4详解】
如图，点P，Q即为所求，使得 ，且相似比为1：2．
【点睛】本题主要考查了勾股定理，勾股定理逆定理，等腰直角三角形的性质，全等三角形的判定，相似三角形的判定，熟练掌握相关定理是解答本题的关键．
（2）在方格纸中画出以线段 为一边的平行四边形 （点G，点H均在小正方形的顶点上），且平行四边形 的面积为4．连接 ，请直接写出线段 的长．
【答案】（1）见解析（2）图见解析，
【解析】
【分析】（1）根据轴对称的性质可得△ADC；
（2）利用平行四边形的性质即可画出图形，利用勾股定理可得DH的长．
【小问1详解】
网格作图
1.（2022丽水中考）如图，在 的方格纸中，点A，B，C均在格点上，试按要求画出相应格点图形．
（1）如图1，作一条线段，使它是 向右平移一格后的图形；
（2）如图2，作一个轴对称图形，使 和 是它的两条边；
（3）如图3，作一个与 相似的三角形，相似比不等于1．
【答案】（1）画图见解析
（2）画图见解析（3）画图见解析
7.（2022牡丹江中考）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC与△DEF关于点O成中心对称，△ABC与△DEF的顶点均在格点上，请按要求完成下列各题．
2024天津中考数学二轮重难题型专题训练 题型三 第18题网格作图题 (含答案)
2024天津中考数学二轮重难题型专题训练题型三第18题网格作图题类型一面积问题典例精讲例1如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上．例1题图(Ⅰ)AB 的长等于________；(Ⅱ)在△ABC 的内部有一点P ，满足S △P AB ∶S △PBC ∶S △PCA ＝1∶2∶3，请在如图所示的网格中，用无刻度．．．的直尺，画出点P ，并简要说明点P 的位置是如何找到的(不要求证明)________________________________________________________________________.【思维教练】(Ⅱ)∵S △P AB ∶S △PBC ∶S △PCA ＝1∶2∶3，∴S △P AB ＝16S △ABC ，S △PBC ＝13S △ABC ，S △PCA ＝12S △ABC ，利用平行线间的距离相等，构造同底等高的三角形，利用面积的倍数关系，分别取AC 的一个六等分点、AC 的一个三等分点，构造AB 、BC 的平行线即可．针对演练1.如图，将△ABC 放在每个小正方形的边长为1的网格中，点A 、B 、C 均落在格点上．第1题图(Ⅰ)△ABC 的面积等于________；(Ⅱ)若四边形DEFG 是△ABC 中所能包含的面积最大的正方形，请你在如图所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法(不要求证明)______________________.2.如图，在每个小正方形的边长为1的网格中，A，B，C均为格点．第2题图(Ⅰ)sin∠ABC的值为________；(Ⅱ)点D，F分别为AB，AC上的点，点A关于DF的对称点为E，且DE∥AC，连接DE，EF分别交BC于点H，G，当S△ADF＝15S△EHG时，请利用无刻度．．．的直尺，在如图所示的网格中，画出点D，F，并简要说明点D，F的位置是如何找到的(不要求证明)________________.3.如图，在每个小正方形的边长为1的网格中，△ABC的顶点均在格点上，点P也在格点上，点C是两个同心圆的圆心．第3题图(Ⅰ)线段AB的长等于________；(Ⅱ)以点C为旋转中心，将△ABC绕点C旋转，点A，B的对应点分别是点D，E，当△PDE的面积取得最小值时，请用无刻度．．．的直尺，在如图所示的网格中，画出点D，E，并简要说明点D，E的位置是如何找到的(不要求证明)_____________________________________. 4.如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．第4题图(Ⅰ)计算AC2＋BC2的值等于____________；(Ⅱ)请在如图所示的网格中，用无刻度．．．的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2＋BC2，并简要说明画图方法(不要求证明)____________________________. 5.如图，在每个小正方形的边长为1的网格中，点A，B都在格点上．第5题图(Ⅰ)线段AB的长等于________；(Ⅱ)在如图所示的网格中，以AB为底边作一个面积为5的等腰三角形ABQ，并简要说明你是怎么画出点Q的(不要求证明)_________________________________________.类型二线段问题典例精讲例2如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上．例2题图(Ⅰ)线段AC的长等于________；(Ⅱ)以AB为直径的半圆的圆心为O，在线段AB上有一点P，满足AP＝A C.请用无刻度．．．的直尺，在如图所示的网格中，画出点P，并简要说明点P的位置是如何找到的(不要求证明)________________________________________________________________________.【思维教练】(Ⅱ)要满足AP＝AC，利用线段垂直平分线的性质，先构造AC的平行线，再利用平行线的性质和直径所对圆心角为90°构造三角形及三角形底边的垂直平分线即可．针对演练1.如图，在每个小正方形的边长为1的网格中，点P ，A ，O 均在格点上，半圆O 的半径为3，PT 与半圆O 相切于点T .第1题图(Ⅰ)∠PTO 的大小＝________(度)；(Ⅱ)请在如图所示的网格中，用无刻度．．．的直尺，画出线段PT ，并简要说明点T 的位置是如何找到的(不要求证明)__________________________________________________________.2.如图，在每个小正方形的边长为1的网格中，△ABC 的顶点A 、B 、C 均在格点上．第2题图(Ⅰ)∠ACB 的大小为________(度)；(Ⅱ)在如图所示的网格中，P 是BC 边上任意一点．以A 为中心，取旋转角等于∠BAC ，把点P 逆时针旋转，点P 的对应点为P ′.当CP ′最短时，请用无刻度．．．的直尺，画出点P ′，并简要说明点P ′的位置是如何找到的(不要求证明)______________________________________.3.如图，在每个小正方形的边长为1的网格中，△ABC 的顶点A ，C 均落在格点上，点B在网格线上，且AB ＝53.第3题图(Ⅰ)线段AC 的长等于________；(Ⅱ)以BC 为直径的半圆与边AC 相交于点D ，若P ，Q 分别为边AC ，BC 上的动点，当BP ＋PQ 取得最小值时，请用无刻度．．．的直尺，在如图所示的网格中，画出点P ，Q ，并简要说明点P ，Q 的位置是如何找到的(不要求证明)_________________________________________.4.如图，在每个小正方形的边长为1的网格中，A、E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点．第4题图(Ⅰ)AE的长等于________；(Ⅱ)若点P在线段AC上，点Q在线段BC上，且满足AP＝PQ＝QB，请在如图所示的网格中，用无刻度．．．的直尺，画出线段PQ，并简要说明点P、Q的位置是如何找到的(不要求证明)________________________________________________________________________.5.如图，在每个小正方形的边长为1的网格中，AB为以点C为圆心的半圆的直径，点A，B，C，P都在格点上，PC交半圆于点D.第5题图(Ⅰ)PD的长等于________；(Ⅱ)点F是半圆上一点(点F不与点A，B重合)，PF与半圆相切于点F，点Q为半圆外一点，QD与半圆相切于点D，且QD＝16．．．的直尺在网格中画出符合条件的点F，Q.5，请用无刻度并简要说明点F，Q的位置是如何找到的(不要求证明)__________________________.6.如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B在格点上，C是小正方形边的中点．第6题图(Ⅰ)AB的长等于________；(Ⅱ)M是线段BC与网格线的交点，P是△ABC外接圆上的动点，点N在线段PB上，且满足PN＝2BN.当MN取得最大值时，请在如图所示的网格中，用无刻度．．．的直尺，画出点P，并简要说明点P的位置是如何找到的(不要求证明)________________________________. 7.如图，在每个小正方形的边长为1的网格中，△OAB的顶点A，B，O均落在格点上，以点O为圆心，OA长为半径的圆交OB于点C.第7题图(Ⅰ)线段BC的长等于________；(Ⅱ)若BD切⊙O于点D，P为OA上的动点，当BP＋DP取得最小值时，请用无刻度．．．的直尺，在如图所示的网格中，画出点D，P，并简要说明点D，P的位置是如何找到的(不要求证明)________________________________________________________________________. 8.如图①，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．(Ⅰ)线段AB的长为________；(Ⅱ)点P是线段AC上的动点．当AP＋5PB最短时，请你在图②所示的网格中，用无刻度．．．的直尺画出点P的位置(保留画图痕迹)，并简要说明画图的方法(不要求证明)________________________________________________________________________.第8题图类型三角度问题典例精讲例3如图，在每个小正方形的边长为1的网格中，△ABC的顶点A在格点上，B是小正方形边的中点，∠ABC＝50°，∠BAC＝30°，经过点A，B的圆的圆心在边AC上．例3题图(Ⅰ)线段AB的长等于________；(Ⅱ)请用无刻度．．．的直尺，在如图所示的网格中，画出一个点P，使其满足∠PAC＝∠PBC＝∠PCB，并简要说明点P的位置是如何找到的(不要求证明)____________________________.【思维教练】(Ⅱ)要确定点P的位置，根据已知∠PAC＝∠PBC＝∠PCB，且点A，B在⊙O 上，从而根据圆的对称性，只需在⊙O上确定点Q，使得点Q与点A关于BO对称，点Q 与点B关于AO对称，再根据∠ABC及∠A的度数确定∠PBC的度数，从而得到点P的位置．针对演练1.如图，是由边长为1的小正方形组成的7×6的网格，△ABC的顶点都在格点上，请仅用无刻度的直尺作图．第1题图(Ⅰ)线段AB的长等于________；(Ⅱ)请在如图所示的网格中，用无刻度．．．的直尺，画出一个格点P ，使∠ABP ＝45°并简要说明画图方法(不要求证明)_________________________________________________________.2.如图，在每个小正方形的边长为1的网格中，点A ，P 分别为正方形边的中点，B 在格点上．第2题图(Ⅰ)线段AB 的长等于________；(Ⅱ)请用无刻度．．．的直尺，在线段AB 上画出一个点Q ，使得点Q 满足∠PQA ＝3∠PQB ，并简要说明点Q 的位置是如何找到的(不要求证明)_______________________________________.3.“三等分任意角”是数学史上一个著名问题．已知一个角∠MAN ，设∠α＝13∠MAN .第3题图(Ⅰ)当∠MAN ＝69°时，∠α的大小为________(度)；(Ⅱ)如图，将∠MAN 放置在每个小正方形的边长为1cm 的网格中，角的一边AM 与水平方向的网格线平行，另一边AN 经过格点B ，且AB ＝2.5cm.现要求只能使用带刻度．．．的直尺，请你在图中作出∠α，并简要说明作法(不要求证明)_________________________________.4.如图，在每个小正方形的边长为1的网格中，△ABC 的顶点B ，C 均落在格点上，点A在网格线上，且AC ＝52.(Ⅰ)线段AB 的长等于________；(Ⅱ)以AB 为直径的半圆与边BC 相交于点D ，在圆上有一点P ，使得BP 平分∠ABC ，请用无刻度．．．的直尺在如图所示的网格中画出点P ，并简要说明点P 的位置是如何找到的(不要求证明)_______________________________________________________.第4题图拓展类型其他问题针对演练1.如图所示，在每个边长都为1的小正方形组成的网格中，点A，B，C均为格点．第1题图(Ⅰ)线段AB的长度等于________；(Ⅱ)点P是△ABC内切圆与AB的切点，请你借助给定的网格，用无刻度．．．的直尺画出点P，并简要说明你是怎么找到点P的(不要求证明)________________________________.2.(2021河东区一模)如图，在由边长都为1的小正方形组成的网格中，点A，B均为格点，C为网格线的三等分点，过点B，C的⊙O与线段AB交于点D.第2题图(Ⅰ)线段AC的长等于________；(Ⅱ)请借助无刻度．．．直尺在给定的网格中画出圆心O，并简要说明你是怎么画出点O的(不要求证明)______________________________________________________________________. 3.如图，在由边长都为1的小正方形组成的网格中，△ABC的顶点A，B，C均落在格点上.第3题图(Ⅰ)线段AB的长为________；(Ⅱ)在AB上找E点使CE⊥AB，请用无刻度．．．的直尺，在如图所示的网格中，画出点E，并简要说明点E的位置是如何找到的(不要求证明)____________________________________.4.如图，在每个小正方形的边长为1的网格中，△ABC的顶点A、B、C均落在格点上．第4题图(Ⅰ)△ABC的面积为________；(Ⅱ)请在如图所示的网格中，用无刻度．．．的直尺在AC上作一点M，使以M为圆心，MC为半径的⊙M与AB相切，并简要说明点M的位置是如何找到的(不要求证明)___________________.参考答案类型一面积问题典例精讲例1(Ⅰ)17；【解析】由勾股定理得AB ＝42＋12＝17.(Ⅱ)如解图，AC 与网格线相交，得点D ，E ；取格点F ，连接FB 并延长，与网格线相交，得点M ，N ，连接DN ，EM 交于点P ，连接PA ，PB ，PC ，则点P 即为所求．例1题解图【解析】∵S △P AB ∶S △PBC ∶S △PCA ＝1∶2∶3，∴S △P AB ＝16S △ABC ，S △PBC ＝13S △ABC ，S △PCA ＝12S △ABC ，作NF ∥AC ，DN ∥BC ,EM ∥AB ，且AE ＝16AC ，CD ＝13AC ，∴S △EAB ＝S △P AB ＝16S △ABC ，S △DBC ＝S △PBC ＝13S △ABC ，∴S △PCA ＝S △ABC －13S △ABC －16S △ABC ＝12S △ABC .针对演练1.(Ⅰ)6；【解析】S △ABC ＝12×4×3＝6.(Ⅱ)如解图，将点B 绕点C 顺时针旋转90°得到点P ，连接PC ，过点A 作PC 的平行线，与BC 交于点Q ，连接PQ 与AC 相交于点D ；过点D 作CB 的平行线，与AB 相交于点E ，分别过点D 、E 作PC 的平行线，与CB 相交于点G 、F .则四边形DEFG 即为所求．第1题解图【解析】找到格点P 的位置，点P 可以看成点B 绕点C 顺时针旋转90°所得，且PC ＝BC ；连接PC ，过点A 作PC 的平行线交BC 于点Q ，连接PQ 交AC 于点D ，此时以D 为顶点很容易作出一个矩形DEFG ，∵∠DQG ＝∠PQC ，∠DGQ ＝∠PCQ ＝90°，∴△DGQ ∽△PCQ ，∴DG ∶PC ＝DQ ∶PQ ，∵四边形DEFG 为矩形，∴DE ∥BC ，∴△ADE ∽△ACB ，∴DE ∶BC ＝AD ∶AC ，而AD ∶AC ＝DQ ∶PQ ，∴DG ∶PC ＝DE ∶BC ，∵PC ＝BC ，则DG ＝DE ，可得矩形DEFG 即为所求的面积最大的正方形．2.解：(Ⅰ)35；【解析】∵AC ＝3，BC ＝4，∠ACB ＝90°，∴AB ＝5，∴sin ∠ABC ＝AC AB ＝35.(Ⅱ)如解图①，取格点M ，N ，连接MN 交网格线于点O ，取格点L ，连接OL 交AC 于点F ，取格点K ，连接KC 交AB 于点D ，则点D ，F 即为所求．图①图②第2题解图【解析】画草图如解图②，∵点A ，E 关于DF 对称，∴DA ＝DE ，∠ADF ＝∠EDF ，∵DE ∥AC ，∴∠EDF ＝∠AFD ，∴∠ADF ＝∠AFD ，∴AD ＝AF ，设AD ＝AF ＝x ，则DE ＝x ，BD ＝5－x ，DH ＝BD ·sin ∠CBD ＝35(5－x )，∴HE ＝DE －DH ＝85x －3，∵∠E ＝∠A ，∴HG ＝HE ·tan E ＝43×(85x －3)，∴S △HEG ＝12HE ·GH ＝23×(85x －3)2，∵S △ADF ＝12AF ·AD ·sin A ＝12x ·45x ＝25x 2，∴25x 2＝15×23(85x －3)2，解得x ＝157或53，∵HE ＝85x －3＞0，∴x ＝157，即AD ＝157，BD ＝207.∴BD ∶AD ＝4∶3，在如解图①中，∵BK AC ＝BD AD ＝43，∴点D 的位置即为所求．∵OF LF ＝123＝16，∴AF ＝2＋17＝157，∴点F 的位置即为所求．3.(Ⅰ)5；【解析】AB ＝42＋32＝5.(Ⅱ)如解图①，取格点F ，G ，H ，I ，分别连接FG ，HI ，与网格线分别交于点J ，K ，作直线JK 分别与小圆、大圆交于点D ，E ，则点D ，E 即为所求．第3题解图①【解析】如解图②，连接CD 、CE 、PE 、PD ，∵△ABC 旋转后点A 、B 的对应点为点D 、E ，∴AB ＝DE ＝5，设点P 到直线DE 的距离为h ，则S △PDE ＝12h ·DE ＝52h ，∴当h 取最小值时△PDE 的面积最小，当DE ⊥CP 时h 最小，即S △PDE 的值最小，则点D ，E 即为所求．第3题解图②4.(Ⅰ)11；【解析】AC ＝12＋12＝2，BC ＝3，∴AC 2＋BC 2＝(2)2＋32＝11.(Ⅱ)如解图，取格点D ，E ，连接AD ，DE ，BE ，取格点H ，I ，连接HI ，交网格线于点J ，取格点K ，连接JK ，交AD 于点M ，取格点O ，P ，连接OP ，交网格线于点Q ，取格点R ，连接QR ，交BE 于点N ，连接MN ，则四边形AMNB 即为所求．第4题解图【解析】如解图，取格点D ，E ，连接AD ，DE ，BE ，构造正方形ADEB ，∵AB ＝12＋42＝17，∴正方形ADEB 的面积为17，且AD ＝BE ＝17，要使以AB 为一边的矩形的面积为11，则矩形的另一边长为111717，则在AD ，BE 上分别截取AM ＝BN ＝111717，则AM DM ＝BN NE＝116＝5.53，取格点H ，I ，连接HI ，交网格线于点J ，取格点K ，连接JK ，交AD 于点M ，则AM DM ＝AJ KD ＝5.53，取格点O ，P ，连接OP ，交网格线于点Q ，取格点R ，连接QR ，交BE 于点N ，则BN NE ＝BQ RE ＝5.53，连接MN ，则四边形AMNB 即为所求．5.(Ⅰ)26；【解析】AB ＝12＋52＝26.(Ⅱ)如解图，取格点C ，E ，F ，连接AC ，EF ，AC 与EF 相交于点M ，取格点D ，S ，T ，连接BD ，ST ，BD 与ST 相交于点N ，连接MN ，取格点L ，P ，连接LP 交MN 于点Q ，连接AQ ，BQ ，则△ABQ 即为所求．第5题解图【解析】如解图，AC ＝BD ＝26，可证CA ⊥AB ，DB ⊥AB ，∴AC ∥BD .∵EC ∥AF ，∴△EMC ∽△FMA ，∴CM AM ＝EC FA ＝85，∴AM ＝513AC ＝52613∵SD ∥BT ，∴△SND ∽△TNB ，∴ND NB ＝SD TB ＝85，∴BN ＝513BD ＝52613.∴AM ＝BN ，∴四边形AMNB 为矩形，易得LP 与AB 互相垂直平分，∴点Q 是MN 的中点，且QA ＝QB ，∴S △ABQ ＝12S 矩形AMNB ＝12AB ·AM ＝5.∴△ABQ 即为所求．类型二线段问题典例精讲例2(Ⅰ)5；【解析】AC ＝12＋22＝5；(Ⅱ)如解图，设BC 与网格线相交于点D ，连接OD 并延长交半圆O 于点E ，连接AE 交BC 于点G ，延长BE ，AC 交于点F ，连接FG 并延长交AB 于点P ，则点P 即为所求．例2题解图【解析】如解图，由BC与网格线相交于点D，得CD＝BD.∵AO＝BO，∴OD为△ABC的中位线，∴OD∥AC，∴∠AEO＝∠CAE.∵AO＝EO，∴∠OAE＝∠AEO.∴∠CAE＝∠OAE，∴AE平分∠FAB.∵AB为半圆O的直径，∴∠AEB＝90°，∴AE⊥BF.∵AE平分∠FAB，∴直线AE垂直平分BF，∴∠FGE＝∠BGE，∴∠PGA＝∠CGA，∵AE平分∠FAB，AG＝AG，∴△APG≌△ACG，∴AP＝AC.针对演练1.(Ⅰ)90；【解析】∵PT是⊙O的切线，∴∠PTO＝90°.(Ⅱ)如解图①，取格点C，连接PC即为切线，切点是T，线段PT即为所求作．第1题解图①【解析】如解图②，取格点H，连接OC，OT，可知PC＝PO＝5，∴△PCO是等腰三角形，∵等腰三角形两个腰上的高相等，∴OT＝CH＝OA＝3，∴PT⊥TO，∴PC是⊙O的切线．第1题解图②2.(Ⅰ)90；【解析】∵AC2＝32＋32＝18，BC2＝42＋42＝32，AB2＝72＋12＝50，∴AB2＝AC2＋BC2，∴△ABC是直角三角形，∴∠ACB＝90°.(Ⅱ)如解图，取格点D，E，连接DE交AB于点T；取格点M，N，连接MN交BC延长线于点G；取格点F，连接FG交TC的延长线于点P′，则点P′即为所求．第2题解图【解析】∵FC ＝22，AC ＝32，∴AF ＝AC ＋CF ＝52，∴AF ＝AB ，∴以点A 为中心，∠BAC 为旋转角，将△ABC 逆时针旋转后点F 即为点B 的对应点．∵点G 为MN 的中点，∴CG ＝322，又∵BC ＝42，AC ＝32，∴FC BC ＝CG AC ＝12，又∵∠ACB ＝∠GCF ＝90°，∴△FCG ∽△BCA ，∴∠F ＝∠B ，∠CGP ′＝∠A ，∴线段FG 即为边BC 旋转后对应边的一部分，∴点P 旋转后的对应点P ′在直线FG 上，∵点T 为AB 的中点，AB 为Rt △ACB 的斜边，∴TC ＝TB ，∴∠TCB ＝∠B ，又∵∠GCP ′＝∠TCB ，∴∠B ＝∠GCP ′，∴∠GCP ′＋∠CGP ′＝∠A ＋∠B ＝90°，∴∠GP ′C ＝90°，即CP ′⊥GF .根据垂线段最短的性质，CP ′即为所求．3.(Ⅰ)13；【解析】AC ＝22＋32＝13.(Ⅱ)如解图①，取格点M ，N ，连接MN ，连接BD 并延长，与MN 相交于点B ′，连接B ′C ，与半圆相交于点E ，连接BE ，与AC 相交于点P ，连接B ′P 并延长，与BC 相交于点Q ，则点P ，Q 即为所求．第3题解图①【解析】如解图②，延长NM 交网格线于点G ，取格点I ，设MN 与直线CI 交于点K ，易知KI ＝23，∴CK ＝1＋23＝53，∵AC ∥MN ，AG ∥CK ，∴四边形CKGA 为平行四边形，∴AG ＝CK ＝53，∵AB ＝53，∴AB ＝AG ，∴BD ＝B ′D ，∵BC 为直径，∴∠BDC ＝90°，∠BEC ＝90°，∴CD 垂直平分BB ′，BE ⊥CE ，∴BP ＝B ′P ，点P 为△BB ′C 的垂心，∴BP ＋PQ ＝B ′P ＋PQ ，B ′Q ⊥BC ，∴BP ＋PQ 的最小值为B ′Q 的长，即点P ，Q 即为所要求的点．第3题解图②4.(Ⅰ)5；【解析】AE ＝22＋12＝ 5.(Ⅱ)如解图，AC 与网格线相交于点P ；取格点M ，连接AM 并延长与BC 相交于点Q .连接PQ ，则线段PQ 即为所求．第4题解图【解析】若以A 为原点建立平面直角坐标系，则A (0，0)，B (6，32)，E (1，2)，F (5，72)，∴直线AE 的解析式为y AE ＝2x ，直线BF 的解析式为y BF ＝－2x ＋272，设P (m ，2m )，Q (n ，－2n ＋272)(0＜m ＜n ＜6)，∴AP 2＝m 2＋(2m )2＝5m 2，PQ 2＝(m －n )2＋(2m ＋2n －272)2，BQ 2＝(n －6)2＋(－2n ＋12)2＝5(n －6)2，∵AP ＝PQ ＝BQ ，∴5m 2＝5(n －6)2，5m 2＝(m －n )2＋(2m ＋2n －272)2，由5m 2＝5(n －6)2得m ＝6－n ，m ＝n －6(舍去)，把m ＝6－n 代入5m 2＝(m －n )2＋(2m ＋2n －272)2，得n ＝92或n ＝632(舍去)，∴P (32，3)，Q (92，92)．5.(Ⅰ)2；【解析】PC ＝32＋42＝5，又∵CD ＝3，∴PD ＝PC －CD ＝2.(Ⅱ)如解图，取格点E ，S ，H ，T ，G ，连接BE 交半圆点F ，连接TD ，SH 并延长交于点Q ，则点F ，Q 为所求点．第5题解图【解析】如解图，连接PE ，CF ，设BE 与CP 交于点R ，∵EG BG ＝86＝43，PB CB ＝43，∴EG BG ＝PB CB.∵∠EGB ＝∠PBC ＝90°，∴△EGB ∽△PBC ，∴∠EBG ＝∠PCB .∵∠EBG ＋∠CBE ＝90°，∴∠PCB ＋∠CBE ＝90°，∴∠CRB ＝90°.∵CF ＝CB ，∴∠PCF ＝∠PCB .∵PC ＝PC ，∴△PFC ≌△PBC ，∴∠PFC ＝∠PBC ＝90°，∴PF 与半圆相切于点F .∵CD ＝CB ，∠PCB ＝∠TCD ，CP ＝CT ，∴△PCB ≌△TCD ，∴∠CDT ＝∠CBP ＝90°，∴QD 与半圆相切于点D .∵HP ∥SC ，HP ＝SC ，∴四边形HPCS 为平行四边形，∴SH ∥CP ，∴TC SC ＝TD QD ，∴54＝4QD.解得QD ＝165.6.(Ⅰ)5；【解析】AB ＝12＋22＝ 5.(Ⅱ)如解图①，取格点T ，连接BT 交△ABC 的外接圆于点P ，则点P 即为所求．第6题解图①【解析】如解图②，连接PC ，由题意知，PN BN ＝CM BM ＝2，∴MN ∥PC ，MN ＝13PC ，∴当PC 取最大值时，MN 取得最大值，∴当PC 是直径时，MN 的值最大，由作图知BP ⊥BC ，∴PC 是圆的直径，则点P 即为所求．第6题解图②7.(Ⅰ)13－3；【解析】BC＝BO－OC＝22＋32－3＝13－3.(Ⅱ)如解图①，取格点E，连接AE与⊙O的交点即为点D，取格点F，连接DF，与OA的交点即为点P.第7题解图①【解析】如解图②，连接BD，OD，设AE与OB交于点M，∵OD＝OA＝3，OM＝OM，又∵OB⊥AE，∴∠DMO＝∠AMO＝90°，∴△DMO≌△AMO(HL)，∴∠DOM＝∠AOM.∵OB ＝OB，∴△DOB≌△AOB(SAS)．∵AB⊥OA，∴BD⊥OD，∵OD为⊙O半径，∴BD为⊙O 的切线；∵点F是点B关于OA的对称点，点P在OA上，∴BP＋DP＝DP＋PF，当点D、P、F三点共线即DP＋PF＝DF时有最小值，此时BP＋DP取得最小值，则点D，P即为所求．第7题解图②8.(Ⅰ)17；【解析】AB＝12＋42＝17.(Ⅱ)如解图①，取格点D并连接AD交网格线于点E，连接BE交AC于点P，则点P即为所求．第8题解图①【解析】如解图②，取格点M ，连接CM ，CM 与网格线交于点J ，可知J 为CM 的中点，连接AJ 与BE 交于点I ，可知BE ⊥AJ ，∵J 为MC 的中点，∴CJ ＝MJ ＝12CM ，∵MC ⊥AC ，AC ＝MC ，∴sin ∠JAC ＝JC AJ ＝55，∴PI AP ＝55，∴PI ＝55AP ，∵AP ＋5BP ＝5(55＋PB )＝5(PI ＋PB )≥5BI ，∴点P 即为所求作．第8题解图②类型三角度问题典例精讲例3(Ⅰ)172；【解析】AB ＝22＋（12）2＝172.(Ⅱ)如解图①，取圆与网格线的交点E ，F ，连接EF 与AC 相交，得圆心O ，设AB 与网格线相交于点D ，连接DO 并延长，交⊙O 于点Q ，连接QC 并延长，与点B ，O 的连线BO 相交于点P ，连接AP ，则点P 满足∠PAC ＝∠PBC ＝∠PCB .例3题解图①【解析】如解图②，取圆与网格线的交点E 、F ，连接EF 交AC 于点O ，∵∠EAF ＝90°，∴EF 为圆的直径，由题意知过点A 、B 的圆的圆心在边AC 上，∴点O 为该圆的圆心，连接DO并延长交⊙O于点Q，连接AQ，BQ，QC，OB，QC的延长线交OB于点P，交AB 于点M，∵点D为AB的中点，∴OD⊥AB，∵∠OAB＝30°，∴∠AOD＝∠BOD＝60°，∴∠AOB ＝120°，∴∠AQB＝60°，∵OD为AB的垂直平分线，∴AQ＝QB，∴△AQB为等边三角形，∴∠QAB＝60°，∵∠CAB＝30°，∴∠QAC＝∠BAC，∴点O为△AQB三个角的平分线的交点，∴∠OBQ＝∠OBA＝30°，∠QOC＝∠BOC＝60°，易得△QOC≌△BOC，∴∠OQC＝∠OBC，∵∠CBA＝50°，∴∠PBC＝∠CBA－∠OBA＝50°－30°＝20°，∴∠OQC＝20°，∴∠PQB＝30°－20°＝10°，∵∠QDM＝90°，∴∠QMD＝90°－20°＝70°，∵∠QMD＝∠ABC ＋∠PCB，∴∠PCB＝70°－50°＝20°，∴∠PCB＝∠PBC，∵∠OBQ＝∠OBA，易得△PBA≌△PBQ，∴∠PAB＝∠PQB＝10°，∴∠PAC＝30°－10°＝20°，∴∠PAC＝∠PBC＝∠PCB＝20°，则点P即为所求．例3题解图②针对演练1.(Ⅰ)5；【解析】AB＝32＋42＝5.(Ⅱ)如解图，取格点P，点P即为所求．第1题解图【解析】如解图，连接PA，PB，由格点P的位置知，PA⊥AB，PA＝AB，则△PAB是等腰直角三角形，则∠ABP＝45°，则点P即为所求．2.(Ⅰ)532；【解析】AB＝12＋（72）2＝532.(Ⅱ)如解图，取格点M，N，连接MN交网格线于点T，连接PT交线段AB于点Q，则点Q 为所求点.第2题解图【解析】如解图，取格点C ，D ，E ，F ，CE ，DF 交于点S ，连接PS ，则PS ⊥AB ，且PS ＝AB ，连接TS ，则TS ⊥PS ，TS ＝PS ，连接PT ，则△PST 为等腰直角三角形，∴∠PTS ＝45°.∵PS ⊥AB ，TS ⊥PS ，∴AB ∥TS ，∴∠PQB ＝∠PTS ＝45°，∴∠PQA ＝135°，∴∠PQA ＝3∠PQB .3.(Ⅰ)23；【解析】∠α＝13∠MAN ＝13×69°＝23°.(Ⅱ)如解图①，让直尺有刻度的一边过点A ，设该边与过点B 的竖直方向的网格线交于点C ，与过点B 的水平方向的网格线交于点D ，保持直尺有刻度的一边过点A ，调整点C 、D 的位置，使CD ＝5cm ，画射线AD ，此时∠MAD 即为所求的∠α.第3题解图①【解析】如解图②，取CD 的中点E ，连接BE ，∵△CBD 是直角三角形，CD ＝5cm ，∴AB ＝BE ＝DE ＝2.5cm ，∴∠BAE ＝∠BEA ＝2∠BDE ，∵BD ∥AM ，∴∠BDE ＝∠DAM ，∴∠DAM ＝13∠NAM .第3题解图②4.(Ⅰ)652；【解析】如解图①，在Rt △AEB 中，AE ＝12，BE ＝4，由勾股定理得AB ＝BE 2＋AE 2＝652.第4题解图①(Ⅱ)如解图①，取AB与格线交点为N，取格点M，G，连接MG与格点交于点H，连接HN 与半圆交于点P，则点P即为所求．【解析】如解图②，连接PB，HC，取格点Q，L，∵AC＝52，∴点A为格线的中点．∵N为AB的中点，AB为半圆的直径，∴点N为半圆的圆心，NL＝12AE.∵点H为MG的四等分点，∴HQ＝NL＝12AE，∴HC∥NB，HC＝NB，∴四边形HCBN是平行四边形，∴HN∥CB，∴∠NPB＝∠PBD，∵PN＝BN，∴∠NPB＝∠NBP，∴∠DBP＝∠NBP，∴BP平分∠ABC，则点P即为所求．第4题解图②拓展类型其他问题针对演练1.(Ⅰ)52；【解析】AB＝12＋72＝5 2.(Ⅱ)如解图，取格点D，E，连接DE交AB于点P，则点P即为所求．第1题解图【解析】由勾股定理得：AC ＝32，BC ＝42，∵AC 2＋BC 2＝18＋32＝50＝AB 2,∴△ABC是直角三角形，且∠ACB ＝90°，设△ABC 内切圆的半径为r ，则有12(AC ＋BC ＋AB )r ＝12AC ·BC ，∴r ＝2，设△ABC 内切圆与AC 的切点为G ，则CG ＝2，根据切线长定理，得AG ＝AP ，∵AG ＝AC －CG ＝22∴AP ＝22，∴BP ＝AB －AP ＝32，∴AP ∶BP ＝2∶3，∴取点A 正下方两格的格点D ，取B 点正上方三格的格点E ，连接DE 交AB 于点P ，则点P 即为所求．2.(Ⅰ)1453；【解析】AC ＝32＋（83）2＝1453；(Ⅱ)如解图，取圆与格线的交点M ，N ，K ，连接MN ，DK ，MN 与DK 的交点O 即为所求作．第2题解图【解析】∵格点D ，K 分别是⊙O 与格线的交点，∠DBK ＝90°，∴DK 是⊙O 的直径，同理知∠MHN ＝90°，∴MN 也是⊙O 的直径，∴MN 与DK 的交点O 即为所求的圆心O .3.(Ⅰ)13；【解析】AB ＝32＋22＝13.(Ⅱ)如解图①，取格点D ，连接DC 并延长与AB 交于点E ，则点E 即为所求．第3题解图①【解析】如解图②，取格点H ，连接BH ，可知AB ⊥BH ，由作图可得DE ∥BH ，∴DE ⊥AB .则点E 即为所求．第3题解图②4.(Ⅰ)6；＝【解析】由题图可判断△ABC为直角三角形，直角边为AC，BC分别长为3,4，则S△ABC1×3×4＝6.2(Ⅱ)如解图，取格点D，连接BD交AC于点M，则点M即为所求．第4题解图【解析】如解图，取格点E，可知A，D，E三点共线，可知AD＝DE，∵AB＝BE＝5，∴BD 是∠ABC的角平分线，∴点M到直线AB的距离等于点M到直线BC的距离即CM，即以M 为圆心，MC为半径的⊙M与AB相切，则点M即为所求．。
中考数学网格作图题的命题立意及解答策略
中考网格作图题的命题立意及解答策略本文对2019年全国各地中考网格作图问题进行梳理, 提炼其命题意图, 并归纳网格作图问题的解题策略, 以期与同行交流探讨。
一、技能立意, 计算作答在格点画图中, 以画图技能立意的试题通常都比较基础, 考查的知识点比较单一, 以格点画图为主要考查目标.例1 (2019年哈尔滨中考题)图1.2是两张形状和大小完全相同的方格纸, 方格纸中每个小正方形的边长均为1, 线段的两个端点均在小正方形的顶点上.(1)在图1中画出以为底边的等腰, 点在小正方形顶点上;(2)在图2中画出以为腰的等腰, 点在小正方形的顶点上, 且的面积为8.分析第(1)问, 要确定格点的位置, 从“形”的角度出发, 点是的垂直平分线和以为直径的圆的交点.从“数”的角度出发, 先由勾股定理, 可以算出, 以为底的等腰直角三角形的腰长, 从而可以确定点的位置(如图3).第(2)问, “画出为腰的等腰”, 既要考虑的情况, 又要考虑的情况, 再根据条件“的面积为8”确定点的位置(如图4).例2 (2019年长春中考题)图5.图6.图7均是的正方形网格, 每个小正方形的顶点称为格点, 小正方形的边长为1, 点均在格点上。
在图5.图6.图7中, 只用无刻度的直尺, 在给定的网格中按要求画图, 所画图形的顶点均在格点上, 不要求写出画法.(1)在图5中以线段为边画一个, 使其面积为6;(2)在图6中以线段为边画一个, 使其面积为6;(3)在图7中以线段为边画一个四边形, 使其面积为9, 且.格点, 如图8(答案不唯一).当底为4时, 面积就为6, 如图9(答案不唯一).第(3)问, 我们知道边长为3的正方形的面积为9, 但不是网格上的边, 我们可用割补法来得到我们想要的图形, 如图10所示, , 则.解题策略在网格中作图, 最基本、最常规的问题就是利用正方形网格的边长为1, 运用勾股定理计算格点线段的长度, 或是利用网格线平行或垂直的基本特征画平行线和垂线.本类型常见的问题跟图形的周长、面积联系比较多, 遇到这类问题的时候, 要先算出周长、面积, 然后利用割补, 平移、旋转等手段来解决.二、思维立意, 分析推理很多格点作图问题, 考查的结果是画图, 实际上是以格点为依托, 把考查逻辑推理能力和分析问题、解决问题的能力融合在一起二例3 (2019年嘉兴中考题)在的方格纸中, 点都在格点上, 按要求画.(1)在图11中找一个格点, 使以点为顶点的四边形是平行四边形;(2)在图12中仅用无刻度的直尺, 把线段三等分(保留画图痕迹, 不写画法).分析第(1)问, 当考虑以为对角线构造平行四边形时, 根据“两组对边分别平行的四边形是平行四边形”, 找到的平行线, 的平行线, 交点即为点.或者根据“两组对边分别相等的四边形是平行四边形”, 找到格点.(如图13, 答案不唯一)第(2)问, 显然在上不能直接找到三等分点.但我们可以另外找到一条三个单位长度的格点线段, 点为的三等分格点.根据“平行线分线段成比例”, 只要过点分别作出的平行线, 就能把线段三等分了。
网格作图题
中考网格作图题专项训练一．填空题（共1小题）1．（2006•烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等_________ ．二．解答题（共17小题）2．作图题，在网格中作图：①过C点作线段CD，使CD∥AB．②过C点作线段CE，使CE⊥AB．3．作图题，在如图所示的网格图中，画出一个与图中三角形相似的三角形．4．作图题：如图，是一个边长为1的正方形网格，请在网格中画出一个边长为2，和3的三角形．（要求三角形的顶点在小格的顶点处）．5．在如图的网格中作图：（1）过点C作直线AB的垂线；（2）过点C作直线AB的平行线．6．基本作图（保留作图痕迹不写作法．）在网格中求作一个三角形A′B′C′，使它与已知△ABC相似，且相似比为1：2；并分别求出两个三角形的周长．7．在如图所示的正方形网格中，已知线段AB，A、B均为格点．（1）请在网格中画出一个以AB为底边的等腰三角形ABC，且点C也为格点；（2）作出△ABC的外接圆（尺规作图，保留作图痕迹，不写作法与证明）．8．正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC，请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并求出这个直角三角形的面积．（要求：三个网格中的直角三角形互不全等）9．（2010•丰台区二模）在正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形，小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，使三个网格中的直角三角形互不全等，并分别求出这三个直角三角形的斜边长．10．△ABC在网格中如图，请根据下列要求作图：（1）过点C作AB的平行线．（2）将△ABC平移，使顶点B平移到点A，画出平移后的三角形．11．作图题：正方形网格中有△OAB，请你以O为位似中心放大，使新图形与原图形的对应线段比是2：1（不写作法）12．如图所示，在8×8的网格中，我们把△ABC在图1中作轴对称变换，在图2中作旋转变换，已知网格中的线段ED、线段MN分别是边AB经两种不同变换后所得的像，请在两图中分别画出△ABC经各自变换后的像，并标出对称轴和旋转中心（要求：不写作法，作图工具不限，但要保留作图痕迹）．13．按下列要求作图：（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上；（2）连接三个格点，使之构成直角三角形（如图1），请在右边网格在作出三个直角三角形，使四个直角三角形互不全等．14．作图：（1）在图1中画出△ABC关于点O的中心对称图形．（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图2正方形网格（每个小正方形边长为1）中画出格点△DEF，使DE=DF=5，EF=．15．如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：（1）画出△ABC中BC边上的高（需写出结论）；（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF；（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积．16．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1．利用网格完成下面的作图：（1）画出点B关于直线AC的对称点D；（2）画出一个格点△A1B1C1，并使它的三边长分别是3、、．17．作图题：（不要求写作法）如图，在边长为单位1的正方形网格中，有一个格点△ABC（各个顶点都是正方形网格的格点）（1）画出△ABC关于直线1对称的格点△A1B1C1；（2）画出以O点为位似中心，把△ABC放大到2倍的△A2B2C2．18．如图，图（1）、图（2）是边长为1的正方形网格，按下列要求作图并回答问题．（1）画出△ABC，点C在格点上且△ABC是等腰三角形，其腰长是_________ ；（2）画出正方形ABCD，且C、D在格点上，其周长是_________ ．2014年5月294464107的初中数学组卷参考答案与试题解析一．填空题（共1小题）1．（2006•烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等如图．考点：作图—复杂作图．专题：压轴题；网格型．分析：本题中得出直角三角形的方法如图：如果设AE=x，BE=4﹣x，如果∠FEG=90°，△AFE∽△GBE。
试论网格作图题的通性通法
试论⽹格作图题的通性通法很多⼈知道天津中考数学有⼀道“奇葩”题——⽹格作图题，此题要求⽤⽆刻度直尺作图，并且还不需要说明作图原理。
很多外省市教师都不能理解此题的意图，包括天津本市也有很多⽼师觉得此题⽆从⼊⼿。
本⼈曾经在天津呆了⼀段时间，⼀直在思考，也⼀直在学习如何突破这道题。
现在将我的思考总结如下，敬请指正。
本⽂分为四部分：第⼀部分：通过⼀个基本问题阐释⽹格作图题的突破点：基本作图。
第⼆部分：通过基本问题的变化感受⽹格作图题的⼀般破解⽅法。
第三部分：通过中考真题的解法对⽐提炼中考题的通性通法。
第四部分：附录该题型命题⼈的⽂章和其他著名教师的解法。
本⽂后半部分需要付费，请谅解，算是给本⼈打字的⾟苦钱，谢谢您。
其实核⼼的内容都在前⾯了。
不感兴趣的读者不⽤看后⾯。
饮酒陶渊明结庐在⼈境，⽽⽆车马喧。
问君何能尔，⼼远地⾃偏。
采菊东篱下，悠然见南⼭。
⼭⽓⽇⼣佳，飞鸟相与还。
此中有真意，欲辨已忘⾔。
基本问题如图，在边长为1的⽹格中⽤⽆刻度的直尺完成以下作图：（1）作出长度为的线段。
（2）过点C作AB的平⾏线。
（3）点点C作AB的垂线。
（4）在AB线段上取⼀点D，使AD:BD=4:3.解题障碍:有点⽆从⼊⼿的感觉，知道尺规作图，但是不知道这种⽆刻度直尺作图。
不理解⽆刻度直尺的含义，不⽤圆规怎么可以画出⽆理线段，看到答案也不明⽩答案为什么成⽴，更不明⽩笔者是怎么想到答案的。
这都是⽹格题的痛点所在。
解题之道：“乾坤⼤挪移”，将⽹格问题转化为常规平⾯⼏何问题解题之术：基本解题顺序是⼀估⼆推三作图。
利⽤4个基本作图破解作图难题，剩下的就是模型分析和推理了。
注重逆向思维的使⽤。
执果索因解题之本：⽹格就相当于是⼀个坐标，直尺上的刻度转化到⽹格上了。
后⾯作图原理是勾股，平⾏，垂直，相似性质得到，其实都是教科书上的基本原理。
这⾥特意提到以下基本概念：格点，⽹格线（格线），格点线段，⾮格点线段，悬空点，悬空线段，补格格点：⽹格线的交点格点线段：图中两端点都是格点的线段⾮格点线段：⾄少有⼀个端点不是格点的线段。
(完整版)网格中的作图题(8年级下)
1． (2015 ·安徽 ) 如图，在边长为 1 个单位长度的小正方(1) ①画出△ ABC向左平移 5 个单位长度后获得的△A1B1C1；形格中，给出了△ABC(极点是格线的交点) ．②画出△ ABC绕着原点O 顺时针旋转90°后获得的△A2B2C2.(1) 请画出△ ABC对于直线l 对(2) 请写出直线B1C1与直线 B2C2的交点坐标．称的△ A1B1C1；(2) 将线段AC 向左平移 3 个单位，再向下平移 5 个单位，画5． (2015 ·昆明盘龙区二模) 如图，△ ABC 三个极点的坐出平移获得的线段A2C2，并以它标分别为A(1 ，1) ， B(4 ， 2) ， C(3， 4) ．为一边作一个格点△A2B2C2，使A2B2＝ C2B2.(1) 请画出将△ ABC先向左，再向下都平移 5 个单位长度后得到的△ A1B1C1；(2) 请画出将△ ABC绕 O按逆时2． (2015 ·昆明二模 ) 在如下图的方格纸中，每个小正针方向旋转90°后获得的△方形的边长都是1，△ ABC和△ A1B1C1成中心对称．A2B2C2；(3) 在 x 轴上求作一点P，使△(1) 请在图中画出对称中PAB周长最小，请画出△PAB并直接写出点P 的坐标．心 O；(2)在图中画出将△A1B1C1沿直线 DE平移 5 格获得的△ A2B2 C2；(3)要使△ A2B2C2与△6． (2013 ·海南 ) 如图，在正方形网格中，△ABC 各极点CC1C2重合，需将△ A2B2C2绕点 C2顺时针旋转，则起码要旋都在格点上，点A、C的坐标分别为( － 5，1) 、( － 1，4) ，转 ________度．联合所给的平面直角坐标系，解答以下问题：3．(2015 ·昆明西山区一模)如图，在平面直角坐标系中，已知△ ABC 的三个极点的坐标分别为A( － 4，3) ，B( －3，1) ， C(－ 1， 3) ． (1) 请按下列要求绘图；①将△ ABC 先向右平移 4 个单位长度，再向上平移 2 个单位长度，获得△ A1B1C1，画出△ A1B1C1；②△ A2B2 C2与△ ABC对于原点O中心对称，画出△A2B2C2.在 (1) 中所得的△ A1B1C1和△ A2B2C2对于点 M 成中心对称，请直接写出对称中心 M点的坐标 ________．4．(2015 ·贵港 ) 如图，已知△ ABC三个极点的(1)画出△ ABC对于 y 轴对称的△A1B1C1；(2)画出△ ABC对于原点 O对称的△A2B2C2；(3)画出△ ABC绕着 O逆时针旋转 90 度得△A3B3C3，则旋转过程中点 C到点C3所经过的路径长 ________( 保存π ) ．7．(2015 ·南宁 ) 如图，在平面直角坐标系中，已知△ ABC 的三个极点的坐标分别为 A( － 1，1) ，B( － 3，1) ，C( －1，4)．(1)画出△ ABC对于 y 轴对称的△ A1B1C1；(2)将△ABC绕着点B 顺时针旋转90°后获得△A2BC2，请在图中画出△ A2BC2，并求出线段 BC旋转过程中所扫过的面积( 结果保存π ) ．参照答案1． (1) 如图：△ A1B1C1即为所求．(2)如图：△ A2B2C2即为所求．5.(1) 如图：△ ABC即为所求． A(－ 3，1) ，B(0 ，2) ，C(－1，4) ．(2) 连结 1 1 1OA， OA， AA 即得△ AOA，图略． S△2.(1) 如图：点 O 即为所求．(2) 如图：△ A2B2C2即为所 1求．(3)90 AOA1＝2×4× 1＝ 2.3．(1) ①如图：△ A1 B1C1即为所求．②如图：△A2 B2 C2即为所求．6． (1) 如图：△ A1B1C1即为所求．(2) 如图：△ A2B2C2即为所求．(3) 如图：△ PAB即为所求， P(2 ， 0) ．(2)(2 ， 1)7.(1) 如图：△ A1B1C1即为所求．(2) 如图：△ A2B2C2即为4.(1) ①如图：△ A1B1C1，即为所求；②如图：△A2B2C2如所求．(3)(1 ， 4) (1 ，－ 4) 17π图所示．(2)( －1，－ 4) ．8.(1) 如图：△ A1 B1C1即为所求．(2) 如图：△ A2BC2即为所求． S＝13π . 4。
网格内的旋转作图
网格中的作图练习
1.如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD 的四个顶点都在格点上，O 为AD 边的中点，若把四边形ABCD 绕着点O 顺时针90º，试解决下列问题： （1）画出四边形ABCD 旋转后的图形；（2）求点C 旋转过程事所经过的路径长；
2. 如图所示，在边长为1的网格中作出 △ABC 绕点A 按逆时针方向旋转90º．
第1题图 第2题图 3. 如图，在边长为1的小正方形组成的网格中， △ABC 的顶点均在格点上：
（1）以直线BC 为对称轴作△ABC 的轴对称 图形，得到△A 1BC ，再将△A 1BC 绕着点B 逆时针 旋转90°得到△A 2BC 1，请依此画出△A 1BC 、△A 2BC 1； （2）求线段BC 旋转到BC 1过程中所扫过
的面积（计算结果用π表示）.
5.画△ABC 绕O 点顺时针方向旋转90°后得到△'
'
'C B A
6．把四边形ABCD 绕O 点逆时针方向旋转90°后得四边形''''D C B A
A
B
C
1.画出四边形ABCD 关于点O 的对称图形.
2. 在网格中作出 △ABC 关于点A 的对称图形
第1题图 第2题图.
3.画出△ABC 关于点O 的对称图形△'
'
'C B A
4．画出四边形ABCD 关于点O 的对称图形四边形''''D C B A。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中考网格作图题专项训练一．填空题（共1 小题）1．（2006?烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：① 在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；② 连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC ．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．二．解答题（共17 小题）2．作图题，在网格中作图：① 过C 点作线段CD，使CD∥AB ．② 过C 点作线段CE，使CE⊥AB ．3．作图题，在如图所示的网格图中，画出一个与图中三角形相似的三角形．4．作图题：如图，是一个边长为1 的正方形网格，请在网格中画出一个边长为2 ，和3 的三角形．（要求三角形的顶点在小格的顶点处）．5．在如图的网格中作图：（1）过点C 作直线AB 的垂线；（2）过点C 作直线AB 的平行线．6．基本作图（保留作图痕迹不写作法．）在网格中求作一个三角形A′B′C′，使它与已知△ABC 相似，且相似比为1：7．在如图所示的正方形网格中，已知线段AB，A、B 均为格点．（1）请在网格中画出一个以AB 为底边的等腰三角形ABC ，且点C 也为格点；8．正方形网格中，小格的顶点叫做格点，小华按下列要求作图：① 在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；② 连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC ，请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三9．（ 2010?丰台区二模）在正方形网格中，小格的顶点叫做格点．小华按下列要求作图：① 在正方形网格的三条不 同实线上各取一个格点， 使其中任意两点不在同一条实线上； ② 连接三个格点， 使之构成直角三角形， 小华在左边 的正方形网格中作出了 Rt △ABC ．请你按照同样的要求， 在右边的两个正方形网格中各画出一个直角三角形， 使三10． △ ABC 在网格中如图，请根据下列要求作图：（ 1）过点 C 作 AB 的平行线．（2）将△ABC 平移，使顶点 B 平移到点 A ，画出平移后的三角形．11．作图题：正方形网格中有 △OAB ，请你以 O 为位似中心放大，使新图形与原图形的对应线段比是 2： 1（不写12．如图所示，在 8×8 的网格中，我们把 △ABC 在图 1 中作轴对称变换，在图 2 中作旋转变换，已知网格中的线段 ED 、线段 MN 分别是边 AB 经两种不同变换后所得的像，请在两图中分别画出 △ABC 经各自变换后的像，并标出13．按下列要求作图：（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上；个网格中的直角三角形互不全等，并分别求出这三个直角三角形的斜边长． 作法）（2）连接三个格点，使之构成直角三角形（如图1），请在右边网格在作出三个直角三角形，使四个直角三角形互不全等．14．作图：（1）在图1 中画出△ABC 关于点O 的中心对称图形．2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图16．如图，在边长为1 个单位长度的小正方形组成的网格中，给出了格点△ ABC（顶点是网格线的交点）和点A 1．利用网格完成下面的作图：（1）画出点B 关于直线AC 的对称点D ；（2）画出一个格点△A 1B1C1，并使它的三边长分别是3、、．2 正方形网格1）中画出格点△DEF ，使DE=DF=5 ，EF= ．每个小正方形边长为15．如图：在正方形网格中有一个△ABC ，按要求进行下列作图（只能借助于网格）（1）画出△ ABC 中BC 边上的高（需写出结论）；17．作图题：（不要求写作法）如图，在边长为单位 1 的正方形网格中，有一个格点△ABC （各个顶点都是正方形网格的格点）2014年5月294464107的初中数学组卷参考答案与试题解析一．填空题（共1 小题）1．（2006?烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：① 在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；② 连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC ．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等如图．考点：作图—复杂作图．专题：压轴题；网格型．分析：本题中得出直角三角形的方法如图：如果设AE=x ，BE=4 ﹣x ，如果∠FEG=90 °，△AFE ∽△ GB EAF ?BG=AE ?BE =x（4﹣x）当x=1 时，AF ?BG=3 ，AF=1 ，BG=3 或AF=3 ，BG=1 当x=2 时，AF ?BG=4 ，AF=1 ，BG=4 或AF=2 ，BG=2 或AF=4 ，BG=1 当x=3 时，AF ?BG=3 ，AF=1 ，BG=3 或AF=3 ，BG=1（同x=1 时）由此可画出另两种图形．解答：解：如图所示：点评：本题中借助了勾股定理，相似三角形的判定和性质等知识来得出有可能的直角三角形的情况，要学会对已学知识点的运用．二．解答题（共17 小题）2．作图题，在网格中作图：① 过C 点作线段CD，使CD∥AB ．② 过C 点作线段CE，使CE⊥AB ．考点：作图—基本作图．分析：① 由于AB 是一个长为3，宽为2 的矩形的对角线，所以过C 点作线段CD ，使CD 也是一个长为3，宽为2 的矩形的对角线；② 过C 点作线 段 CE ，使 CE 是一个长为 6， 宽为 4 的矩形的 对角线．解答： 解： ①② 如下图所示：点评： 本题考查了平 行线的作法， 垂 线的作法， 掌握 网格结构的特 点并熟练应用 是解题的关键．作图 —相似变 换；相似三角形 的性质． 网格型． 利用相似三角 形的性质， 对应 边的相似比相 等，对应角相 等，可以让各边 长都放大一倍， 得到新三角形． 解：作图题（符 合题目意思即可）．专题 ：分析：解答：3．作图题，在如图所示的网格图中，画出一个与图中三角形相似的三角形．考点：的画法，注意做这类题时的关键是对应边相似比相等，对应角相等．4．作图题：如图，是一个边长为1 的正方形网格，请在网格中画出一个边长为2 ，和3 的三角形．小格的顶点处）．勾股定理．关键是找出2 ，的长度，可利用勾股定理求出这些长度，从而画出三角形．解：2 看作是2、2 为直角边的直角三角形的斜边．可看作是以2和1 为直角边的直角三角形点评：本题主要考查了相似三角形的斜边，从而可画出三角形．AC= ，BC=3 ．要求三角形的顶点在考点：分析：解答：△ ABC 符合要求．点评：本题考查勾股定理的应用，关键是用勾股定理求出斜边长，从而画出符合要求的三角形．5．在如图的网格中作图：（1）过点C 作直线AB 的垂线；（2）过点C 作直线AB 的平行线．考点：作图—基本作图．分析：根据网格结构的特点，利用直线与网格的夹角的关系找出过C 与AB 垂直的格点以及平行的格点作出即可．解答：解：如图所示：l ⊥ AB ，m∥ AB ．点评：本题考查了平行线的作法，垂线的作法，掌握网格结构的特点并熟练应用是解题的关键．6．基本作图（保留作图痕迹不写作法．）在网格中求作一个三角形A′B′C′，使它与已知△ABC 相似，且相似比为1：2；并分别求出两个三角形的周长．考点：作图—相似变换．专题：作图题．分析：利用勾股定理分别求出AB ，AC 及BC 的长，截取A′B′=2AB，B′C′=2BC，连接A′C′即可得到三角形A ′B′C′，求出两三角形周长即可．解答：解：做出△A ′B′C′，如图所示，利用勾股定理得：AB= =，AC= =3 ，BC=2 ，∴A ′B′=2AB=2 ，A′C′=2AC=6 ，B′C′=4，则△ ABC 周长为+3 +2 ，△A ′B′C′的周长为2 +6 +4 ．此题考查了作 图﹣相似变换， 以及勾股定理， 做出相应的图 形是解本题的 关键．考点： 作图 —复杂作图．分析： （ 1）利用网格作出 AB 的垂直 平分线， 再作等腰三角形即可； （ 2）以 AB 的 垂直平分线与 AB 的交点 M 为 圆心，以 AM 为 圆心画圆即可．解答： 解：如图所示：7．在如图所示的正方形网格中，已知线段 AB ，A 、B 均为格点．（1）请在网格中画出一个以 AB 为底边的等腰三角形 ABC ，且点 C 也为格点；点评：了复杂作图， 关键是掌握线段 垂直平分线上 的点到线段两 点的距离相等．8．正方形网格中，小格的顶点叫做格点，小华按下列要求作图：① 在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；② 连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了 Rt △ABC ，请你按照同样的要求， 在右边的两个正方形网格中各画出 角形，并求出这个直角三角形的面积． （要求：三个网格中的直角三角形互不全等）考点： 作图 —代数计 算作图．专题 ： 网格型．分析： 画的直角三角 形的三边应符 合两直角边的 平方和等于斜 边的平方． 第一 个图形和第二 个图形的面积 可让两条直角 边的积 ÷2 即可．解答： 解：画二个图供参考：点评：个直角三（每个图画对（3 分），面积计算正确得（1 分），两种情况共8 分）易得图1 三边长为、、，符合两边和的平方等于第三边的平方，面积为：× × =5；图2 中三边长分别为、符合两边和的平方等于第三边的平方，面积为：× × =3．点评：本题主要考查直角三角形的格点画法需满足的条件；直角三角形的三边应符合两直角边的平方和等于斜边的平方．9．（2010?丰台区二模）在正方形网格中，小格的顶点叫做格点．小华按下列要求作图：① 在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；② 连接三个格点，使之构成直角三角形，小华在左边的正方形网格中作出了Rt△ABC ．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，个网格中的直角使三三角形互不全等，并分别求出这三个直角三角形的斜边长．考点：作图—应用与设计作图．分析：可以利用三角板，移动位置，即可作出图形，然后利用勾股定理即可求得斜边解答：解：下面给出三种参考画法：（画图正确每个（1 分），斜边计算正确每个（1分），共5 分）斜边AC=5 ，斜边AB=4 ，斜边DE= ，斜边MN= ．点评：本题主要考查了作图，正确利用三角板是解题的关键．10．△ ABC 在网格中如图，请根据下列要求作图：（1）过点C 作AB 的平行线．（2）将△ABC 平移，使顶点B 平移到点A，画出平移后的三角形．考点：作图-平移变换；作图—基本作图．分析：（1）作出AB 的平行线即可；（2）根据网格结构找出点A 、B、C 平移后的对应点，然后顺次连接即可．解答：解：（1）（2）所作图形如下所示：本题考查了平 移作图的知识， 解答本题的关 键是掌握平移 变换的特点， 准 确找出平移后 各点的位置．11．作图题：正方形网格中有 △OAB ，请你以 O 为位似中心放大，使新图形与原图形的对应线段比是 考点： 作图 -位似变换．分析： 画△ OCD ，根据题意位似中心 已知为 O ，则延 长AO ，BO ，根 据相似比， 确定 所作的位似图 形的关键点 C 、 D ，再顺次连接 所作各点， 即可 得到放大一倍 的图形△ CDO ；解答：解：如图：分别延长 AO ，BO 到点 C ， D 使OC=2AO ，OD=2BO ， 顺次连接即得 △OCD 点评： 2：1（不写作法）点评： 此题考查了画位似图形的画 法．画位似图形 的一般步骤为：① 确定位似中 心，② 分别连接 并延长位似中心和能代表原 图的关键点； ③ 根据相似比， 确 定能代表所作的位似图形的 关键点； 顺次连 接上述各点， 得 到放大或缩小 的图形．12．如图所示，在 8×8 的网格中，我们把 △ABC 在图 1 中作轴对称变换，在图 ED 、线段 MN 分别是边 AB 经两种不同变换后所得的像，请在两图中分别画出 对称轴和旋转中心（要求：不写作．考点： 作图 -轴对称变换；作图 -旋转变换． 专题 ：作图题． 分析： （1）连接 BD 和AE ，后连接GH ，则 GH 即为轴对称变换 的对称轴， 作点 C关于 GH 的对称点， 然后顺次 连接各点即可； （2）先根据线 段 AB 经旋转变 换后得到 MN ， 找出旋转中心 和旋转方向， 然 后根据旋转规 律找出旋转后 的各点， 顺次连 接各点即可．解答： 解：所画图形如 下所示：2 中作旋转变换，已知网格中的线段 △ABC 经各自变换后的像，并标出其中GH 为轴对称变换的对称轴，△DEF 与△ BAC 关于直线GH 对称；点O为旋转变换的旋转中心，△ MNP 由△ ABC 以点O 为旋转中心，顺时针旋转90°得到．点评：本题考查轴对称变换和旋转变换的知识，难度适中，解题关键是对这两种变换的熟练掌握以便灵活运用．13．按下列要求作图：（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上；（2）连接三个格点，使之构成直角三角形（如图1），请在右边网格在作出三个直角三角形，使四个直角三角形互不全等．考点：作图—复杂作图．专题：网格型．分析：本题主要利用直角三角形的性质来画，可利用勾股定理也可利用网格来画．解答：解：三角形边长只能是其中能组成直角三角形有：（1）；（2）；（3）；（4）；（5）；（已作）（6）；（7）；（8）；（9）点评：本题主经考查了勾股定理和网格的综合运用能力．14．作图：（1）在图1 中画出△ABC 关于点O 的中心对称图形．2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图考点：作图-旋转变换；勾股定理．专题：作图题．分析：（1）画出A 、C 三点关于O 的对称点，连接各对称点所得图形即为△ ABC 关于点O 的中心对称图形．（2）找到直角边位1 和3 的直角三角形，其斜边为，易作出DE=DF=5 ．解答：解：（1）如图（1）：（2）如图（2）：EF= =；DF= =5 2 正方形网格1）中画出格点△DEF ，使DE=DF=5 ，EF= ．每个小正方形边长为本题考查了作 图﹣﹣旋转变 换和勾股定理， 充分利用格点 是解题的关键 一步．15．如图：在正方形网格中有一个 △ABC ，按要求进行下列作图（只能借助于网格）1）画出 △ ABC 中 BC 边上的高（需写出结论） ；2）画出先将 △ABC 向右平移 6格，再向上平移 3格后的 △DEF ；3）画一个锐角 △MNP （要求各顶点在格点上） ，使其面积等于 △ABC 的面积．换．专题 ： 网格型．分析： （ 1）过点 A 作AG ⊥BC ，交 CB 的延长线于点 G ， AG 就是所 求的 △ ABC 中 BC 边上的高；（ 2）把 △ABC 的三个顶点向 右平移 6 格，再 向上平移 3 格即 可得到所求的 △DEF ；（3）画一个面 积为 3 的锐角三 角形即可．点评：解答：解：就是所求的△ ABC 中BC 边上的高．用到的知识点为：一边上的高为这边所对的顶点向这边所引的垂线段；图形的平移要归结为各顶点的平移；各个角都是锐角的三角形叫做锐角三角形．点评：16．如图，在边长为1 个单位长度的小正方形组成的网格中，给出了格点△ ABC（顶点是网格线的交点）和点A 1．利用网格完成下面的作图：（1）画出点B 关于直线AC 的对称点D ；（2）画出一个格点△A 1B1C1，并使它的三边长分别是3、、．考点：作图-轴对称变换；勾股定理．分析：（1）过点B 作BE ⊥AC 于点E，延长ED，在直线BE 上取点D，使DE=BE ，则点D 即为所求点；（2）根据勾股定理画出格点△A 1B1C1，并使它的三边长分别是3、、即可．解：（1）、（2）如图所示．本题考查的是作图﹣轴对称变换，熟知轴对称图形的作法及勾股定理是解答此题的关键．17．作图题：（不要求写作法）如图，在边长为单位 1 的正方形网格中，有一个格点△ABC （各个顶点都是正方形网格的格点）（1）画出△ABC 关于直线1 对称的格点△A1B1C1；（2）画出以O 点为位似中心，把△ABC 放大到2 倍的△A2B2C2．考点：作图-位似变换；解答：点评：作图-轴对称变换．专题：作图题；压轴题．分析：（1）分别找到直线l 的距离与点A，B，C 各点到直线l 的距离相等的各对应点，顺次连接即可；（2）延长AO 到A 2，使A20=2OA ，得到A的A2，同法得到其余点的对应点，顺次连接即为所求图形．解答：解：如图（画正确一个得（3 分），共6 分）点评：两图形关于某条直线对称，对应点的连线被这条直线垂直平分；位似变换的关键是根据位似中心和位似比确定对应点的位置．18．如图，图（1）、图（2）是边长为1 的正方形网格，按下列要求作图并回答问题．（1）画出△ABC ，点C 在格点上且△ABC 是等腰三角形，其腰长是；（2）画出正方形ABCD ，且C、D 在格点上，其周长是 4 ．考点：作图—应用与设计作图；勾股定理．分析：（1）首先根据题意画出图形，再利用勾股定理计算出腰长即可；（2）首先根据题意画出图形，再根据勾股定理求出正方形的边长，进而得到周长．解答：解：（1）如图（1）所示：AB= =，故答案为：；（2）如图（2）所示；AB= =，周长为4× =4 ．故答案为：4．点评：此题主要考查了应用作图，以及勾股定理，关键是正确根据题目要求画出图形．。