(完整版)和差问题(一)教案
和差问题教案
和差问题教案教案内容：和差问题一、教学目标：1. 了解和差问题的概念及解题思路；2. 能够熟练运用和差问题的解法，解决相关问题。
二、教学重难点：1. 和差问题的解题思路；2. 运用所学知识解决和差问题。
三、教学准备：教师准备问题较为简单的和差问题，白板、黑板或投影仪等教学工具。
四、教学过程：步骤一：引入新知识1. 引导学生回顾一下加减法的概念及运算方法。
2. 提问：在数学中，什么是和差问题？3. 学生回答后，教师给出解释：和差问题是指在计算过程中，我们需要计算两个数的和或差。
解决和差问题可以通过多种解法，下面我们来学习一种常用的方法。
步骤二：学习和差问题的解题方法1. 教师精心准备一些简单的和差问题，例如：35 + 20 = ?；58 - 23 = ?；2. 教师解读问题，指导学生分别使用加法和减法来计算并解答问题。
3. 提示学生观察和分析计算过程，总结出解决和差问题时的解题方法。
4. 教师给出合理的解题思路和步骤：对于加法问题，我们可以先将两个数的个位数相加，然后再将十位数相加；对于减法问题，我们可以先计算个位数的差，再计算十位数的差。
5. 展示更复杂一些的和差问题，并指导学生按照解题思路依次计算并解答。
步骤三：巩固和拓展1. 教师出示几道带有和差问题的练习题，请学生独立完成。
2. 学生完成后，教师进行答案讲解，指导学生解题思路和方法。
3. 提醒学生要注意计算过程的准确性和逻辑性。
五、课堂小结：1. 学生回顾和差问题的概念及解题方法；2. 教师强调解决和差问题的思维逻辑和解题步骤；3. 学生通过练习巩固所学知识，并提出问题或困惑。
六、作业布置：1. 布置适量的和差问题练习题作为课后作业，要求学生用正确的解题方法解答问题。
2. 鼓励学生多思考、多实践，提高解决和差问题的能力。
七、板书设计：和差问题解题思路：加法问题先个位相加，再十位相加；减法问题先个位相减，再十位相减。
四年级数学-和差问题 第一课时-1教案
第八单元第3课时：和差问题第一课时一、教学背景简述本节课的重难点是：运用画图的策略，理解和差问题的特点和解题思路，掌握和差问题的解题方法。
对于学生来说，只知道两个量的和与差，要想知道两个量分别是多少？光靠想还是有一定困难的。
三年级时，学生学习了归一问题、连乘问题、逆推问题等各种类型的两步实际问题，积累了画图分析、解决问题的策略。
这些画图的策略对学生来说是非常重要的，能够帮助学生很好地解决和差问题。
不过，对于解决问题背后的转化思想可能有的学生还认识的不够。
二、学习目标1．经历运用列举、画图策略整理条件和问题，分析数量关系，解决问题的过程。
2．在探究和合作交流活动中，感受列表、画图策略的价值，能解决简单的实际问题。
3．在合作交流中激发自主探究、与他人合作交流的意识。
三、教学过程（一）创设情境，明确问题。
我们听过很多读书的名言，顾炎武说：“读万卷书，行万里路”，高尔基说：“书是人类进步的阶梯”，很多名人都说了读书的好处，现在啊，同学们看的书也越来越多了，我们吸取书中的营养，丰盈我们的大脑！那么，读书的过程中是不是也存在着数学问题呢？接下来，我们就一起来看一看姐姐和妹妹两人的读书情况。
请学生观察，交流知道的信息，并提出问题。
学生发现信息：这半年，姐姐和妹妹一共看书23本，姐姐比妹妹多看7本。
学生提出问题：姐姐和妹妹分别看了多少本？小结：看来，知道两个数量和与差。
就能研究两个数量是多少。
今天我们就解决这样的和差问题。
学生提出困惑：如果有姐姐看的本数，我就能求出妹妹的，如果有妹妹看的本数，我就能求出姐姐的，现在，姐姐和妹妹的本数都没有，怎么办呢？是啊，这怎么办呢？请你开动脑筋，在任务单或练习本上试一试吧。
（二）自主探究汇报交流。
1.学生独立尝试。
2.全班交流展示（1）展示学生列表方法方法一：方法二：小结：通过这样不断地尝试、调整，最终就知道了妹妹看了8本，姐姐看了15本。
用列表的方法很好地解决了问题。
（2）展示学生画图列式计算方法：方法一：方法二：3.回顾与反思。
和差问题 教案
和差问题教案教案标题：和差问题教案教案目标：1. 学生能够理解和差问题的概念，并能够运用适当的方法解决这类问题。
2. 学生能够灵活运用和差问题解决实际生活中的情境。
教学目标：1. 知识目标：学生能够掌握和差问题的定义和基本解法。
2. 技能目标：学生能够运用和差问题解决实际问题。
3. 情感目标：培养学生的逻辑思维能力和解决问题的兴趣。
教学重点：1. 理解和差问题的概念。
2. 掌握和差问题的基本解法。
教学难点：1. 运用和差问题解决实际问题。
教学准备：1. 教师准备：教师需要准备和差问题的相关题目和解答，以及教学课件。
2. 学生准备：学生需要准备纸和笔。
教学过程：Step 1: 引入（5分钟）1. 教师可以通过提问的方式引入和差问题，例如：“小明有5个苹果，小红有3个苹果，他们一共有多少个苹果？”2. 引导学生思考这个问题，鼓励他们用不同的方法解决。
Step 2: 概念讲解（10分钟）1. 教师向学生介绍和差问题的概念，即两个数的和或差的问题。
2. 通过具体的例子解释概念，例如：“小明有5个苹果，小红给了他3个苹果，那么小明现在有多少个苹果？”3. 引导学生发现和差问题的特点和解决方法。
Step 3: 解题方法（15分钟）1. 教师向学生讲解和差问题的基本解法，包括加法和减法。
2. 通过示例演示解题过程，引导学生理解解题思路。
3. 鼓励学生多思考，多尝试不同的解题方法。
Step 4: 练习与巩固（20分钟）1. 学生进行课堂练习，解决一些基础的和差问题。
2. 教师巡回指导学生，及时纠正他们的错误，鼓励他们互相讨论解题方法。
3. 针对不同的学生，教师可以提供不同难度的练习题，以巩固学生的学习效果。
Step 5: 拓展应用（10分钟）1. 教师设计一些实际生活中的情境问题，让学生运用和差问题解决。
2. 鼓励学生思考问题的多种解决方法，并能够合理解释自己的思路。
Step 6: 总结与反思（5分钟）1. 教师与学生一起总结和差问题的解题方法和思路。
和差问题(一).教师版
1. 会判断什么样的应用题属于和差问题：已知两个数的和以及两个数的差，要分别求这两个数；2. 并掌握和差问题的特性，为以后继续学习和倍、差倍问题做准备；3. 总结归纳出解决和差问题的方法，并解决一些实际问题．和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题。
为了解答这种应用题，首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”。
知道两个数的和，以及它们的差，要求这两个数，解决和差问题需要我们画线段图来分析，方法如下：(两数的和－两数的差)÷2=较小的数 较小的数+两数的差=较大的数(两数的和+两数的差)÷2=较大的数 较大的数－两数的差=较小的数【例 1】 一辆公交车里有30位乘客，到大桥站有17人下车，又上来19人，现在车上和原来比，人多了还是少了，多（或少）几个人？【考点】基本的和差问题 【难度】1星 【题型】解答【解析】 这道题有两种不同的思维方法．方法一：先求出现在车上有多少人，再和原来车上30人进行比较，就知道人多了还是人少了，再用减法计算，就能求出多或少了几个人．列式：现在车上人数：30171932-+=（人），现在车上比原来多几人？32302-=（人）方法二：聪明的学生会想到只要把下车和上车的人数进行比较，就知道答案了，因为下车17人，上车19人，上车的人比下车的多2人．这样原来车上的“30人”就是多余条件了．列式：19172-=（人），现在车上人多了，多2人．【答案】现在车上人多了，多2人【巩固】 在月球表面，白天阳光垂直照射的地方的温度高达127℃，夜晚的温度下降到零下183℃，则月球表面昼夜温差（最高与最低温度的差）是 ℃。
【考点】基本的和差问题 【难度】1星 【题型】填空【关键词】希望杯，4年级，1试【解析】 127+183=310【答案】310【巩固】 最新的科学探测表明：火星表面的最高温度约为5℃，最低温度约为零下15℃，则火星表面的温差（最高与最低温度的差）约为 ℃。
专题一 和差问题个性化教案(1)
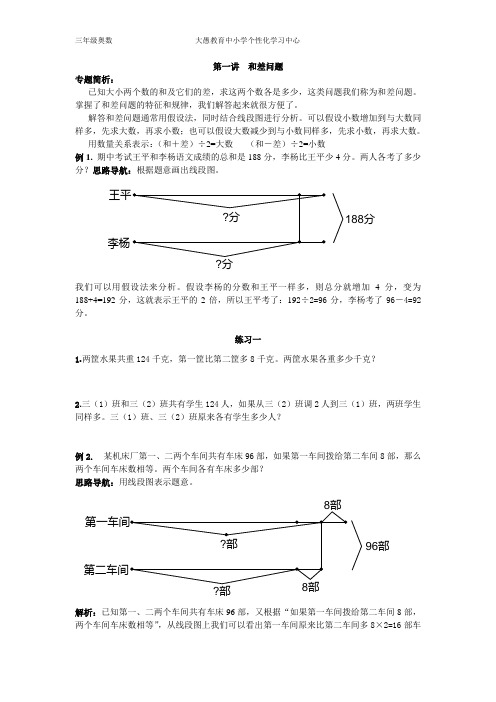
第一讲 和差问题专题简析：已知大小两个数的和及它们的差，求这两个数各是多少，这类问题我们称为和差问题。
掌握了和差问题的特征和规律，我们解答起来就很方便了。
解答和差问题通常用假设法，同时结合线段图进行分析。
可以假设小数增加到与大数同样多，先求大数，再求小数；也可以假设大数减少到与小数同样多，先求小数，再求大数。
用数量关系表示：（和＋差）÷2=大数 （和－差）÷2=小数例1. 期中考试王平和李杨语文成绩的总和是188分，李杨比王平少4分。
两人各考了多少分？思路导航：根据题意画出线段图。
188分?分?分李杨王平我们可以用假设法来分析。
假设李杨的分数和王平一样多，则总分就增加4分，变为188+4=192分，这就表示王平的2倍，所以王平考了：192÷2=96分，李杨考了96－4=92分。
练习一1.两筐水果共重124千克，第一筐比第二筐多8千克。
两筐水果各重多少千克？2.三（1）班和三（2）班共有学生124人，如果从三（2）班调2人到三（1）班，两班学生同样多。
三（1）班、三（2）班原来各有学生多少人？例2. 某机床厂第一、二两个车间共有车床96部，如果第一车间拨给第二车间8部，那么两个车间车床数相等。
两个车间各有车床多少部？思路导航：用线段图表示题意。
8部8部96部?部?部第二车间第一车间解析：已知第一、二两个车间共有车床96部，又根据“如果第一车间拨给第二车间8部，两个车间车床数相等”，从线段图上我们可以看出第一车间原来比第二车间多8×2=16部车床。
所以，第一车间原有：（96+8×2）÷2=56部，第二车间原有56－8×2=40部。
练习二1.红星小学一年级新108人，分成甲、乙两个班。
如果从甲班转3个学生到乙班去，两班学生就一样多。
甲、乙两班各有学生多少人？2.有三只船共运木板9800块，第一只船比其余两船共运的少1400块，第二只船比第三只船少运200块。
和差问题( 教案 )
和差问题（教案）教学目标1.能够理解较为简单的和差问题2.能够独立解决小学阶段的和差问题3.能够应用所学知识解决实际问题教学重点1.理解和差问题的概念2.应用和差问题解决实际问题教学难点应用和差问题解决实际问题教学准备黑板，彩笔，教材，练习题教学过程Step1 引入新课教师：同学们，我们上节课学习了有关数学的一些知识，比如说加减乘除，小学数学我们学习了很多知识，你们知道奇数和偶数吗？今天我们学习的是和差问题。
大家知道，俗话说得好，学好数学，走遍天下都不怕。
那么今天我们就来学习和差问题吧！Step2 学习和差问题的概念教师：同学们，你们知道和差问题什么意思吗？今天就让我们来认识一下和差问题。
和差问题是指通过加减或者其他运算方法得出的结果。
我们可以先来看一下这个问题，小明去花园里采摘到了15个苹果，小红采摘到了10个苹果，那么他们两个人采摘到的苹果总数是多少呢？（教师在黑板上画出一个条形思维图：小明采摘到apple=15，小红采摘到apple=10，然后在最下面写上2个大括号，中间写上+，最后根据加法原理，写出答案：25）这就是一个最基本的和问题。
教师：大家知道差问题又是什么吗？那么我们再来看一下这个问题，小明有20个苹果，他送给了小红5个苹果，那么小明现在还有多少个苹果呢？（教师在黑板上画出一个条形思维图：小明有apple=20，送给小红apple=5，中间写上-，然后根据减法原理，得出答案：15），这就是一个最基本的差问题。
Step3 练习和差问题教师：同学们，现在开始我们来做一些和差问题的练习。
请拿起笔和本子，认真思考每一个问题。
（教师给学生发下面的练习题）：练习题：1.小丽有5块钱，她买了一支笔芯，花了1块钱，请问她还剩下多少钱？（差问题）2.小明和小亮一共有12个橘子，小明有比小亮多2个橘子，请问小明有几个橘子？（差问题）3.张三和李四一起做了20道题，张三做了8道题，问李四做了几道题？（差问题）4.小燕同学和小红同学一共剪了20个纸片，小燕同学剪了4个，那么小红同学剪了几个呢？（差问题）5.小华妈妈请了小华7个朋友来家里做客，那么一共有多少人来家里做客呢？（和问题）6.小丽和小美一共篮球比赛投了15个篮球，小丽投了8个，请问小美投了几个？（差问题）7.小明下午从学校到家里走了20分钟的路程，而他上午走的路程是下午的一半，请问小明上午走了多少分钟的路程？（差问题）教师：请大家认真思考，完成所有的问题，如果有不懂的可以随时举手提问。
(完整版)和差问题教案
和差问题教案教学目标1.会判断什么样的应用题属于和差问题．已知两个数的和以及两个数的差，要分别求这两个数就属和差问题，并掌握和差问题的特性，为以后继续学习和倍、差倍问题做准备．2.总结归纳出解决和差问题的方法，并解决一些实际问题．基本概念：已知几个数的和与差，求这几个数的应用题，叫和差问题。
基本思路：通常采用假设的方法，就是假设那个较小的数和较大的数相等或者假设那个较大的数和那个较小的数相等，这样就会引起总数（和）的变化（增加或减少），求出新的和，平均分就可得其中的一个数。
为了解答这种应用题，首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”。
关键问题：求出同一条件下的和与差。
基本公式：①（和-差）÷2=较小数较小数+差=较大数和-较小数=较大数②（和+差）÷2=较大数较大数-差=较小数和-较大数=较小数知识点拨：和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题。
例1：两筐水果共重150千克，第一筐比第二筐少10千克，两筐水果各多少千克？1、读题，找出条件和问题。
2、根据条件和问题画出线段图3、想一想假设两筐的水果一样重好求吗？（总重量÷2）4、假设把第二筐多的10千克减掉，看成两个第一筐的重量来计算，总重量要变成多少？怎么计算？列式：第一筐：15010270（）（千克）-÷=第二筐：701080+=（千克）5、假设把第一筐少的10千克补上，看成两个第二筐的重量来计算，总重量要变成多少？怎么计算？列式：第二筐：15010280（）（千克）+÷=第一筐：801070-=（千克）6、小结：知道两个数的和，以及它们的差，要求这两个数，解决和差问题需要我们画线段图来分析，方法如下：方法一： (和+差)÷2=大数和-大数=小数方法二： (和-差)÷2=小数和-小数=大数巩固练习：（1）甲、乙两人同时以相同的速度打字，2分钟共打了240个字，已知甲每分钟比乙多打10个字．问甲、乙两人每分钟各打多少个？问：题目中知道了什么条件？问：“已知甲每分钟比乙多打10个字”这个条件告诉我们甲、乙两人每分钟打字的什么？问：根据“2分钟共打了240个字”可以求出什么？（甲、乙两人一分钟就打了2402120÷=（个））师：这实际上就知道了甲、乙两人每分钟打字的和，这样就转换成典型和差问题了．方法一：甲：240210265（）(个)÷+÷=乙：651055-=(个)方法二：乙：240210255（）(个)÷-÷=甲：551065+=（个）在研究完这两种方法以后，老师要注意引导学生来总结和差问题的解决方法．解答和差问题的应用题，可以先画出线段图，从线段图上找到大数和小数，并找到解决方法．(两数的和－两数的差)÷2=较小的数较小的数+两数的差=较大的数(两数的和+两数的差)÷2=较大的数较大的数－两数的差=较小的数（2）果园共260棵桃树和梨树，其中桃树的棵数比梨树多20棵．桃树和梨树各有多少棵？方法一：桃树：260202140-=（棵）（）（棵）梨树：14020120+÷=方法二：梨树：260202120（）（棵）桃树：12020140+=（棵）-÷=（3）有一根钢管长12米，要锯成两段，使第一段比第二段短2米．每段各长多少米？第一段：12225-= (米)-÷=（） (米) 第二段：1257（4）陈红和李玲平均身高为130厘米，陈红比李玲高8厘米，陈红和李玲身高各是多少厘米？陈红和李玲平均身高为130厘米，她们身高的和为：1302260⨯= (厘米) 方法一：陈红：2608 2 134-= (厘米)+÷=（） (厘米) 李玲：1348126方法二：李玲：2608 2 126+=（厘米）（） (厘米) 陈红：1268134-÷=明差问题例一：买一支自动铅笔与一支钢笔共用10元，已知铅笔比钢笔便宜6元，那么买铅笔花多少元？钢笔的价钱：元10元自动铅笔的价格：？元 6元解法一：假设铅笔与钢笔价钱相同（假设都是钢笔），买一支钢笔、一支铅笔共花10+6=16（元），这是两支钢笔的钱。
小学数学《和差问题》教案
和差问题一、趣味数学导入，激发兴趣（1）、有一个人带着猫、鸡、米过河，船除需要人划外，至少能载猫、鸡、米三者之一，而当人不在场时猫要吃鸡，鸡要吃米。
试设计一个安全过河方案，并使渡船次数尽量减少。
答案:1 带鸡过去 空手回来2 带猫过去 带鸡回来3 带米过去 空手回来4 带鸡过去（2）、24个人排成6列，要求5个人为一列，你知道应该怎样来排列吗？ 5×6-24=6所以有6个人必须在交叉点上。
排成一个正六边形每条边5个，刚好6个顶点是交叉点。
二、例题讲解例1 甲、乙两班共有学生84人，如果从甲班调6人到乙班，则两班人数相等，原来甲、乙各有多少人？1、理解题意从题目中告诉我们的信息，可以通过画线段图来把题目中的已知信息和需要解决的信息清晰的表示出来。
乙： 甲：2、分析题意从题目中已知的条件可以知道，从甲板调6人，两个班人数相等，可以知道甲班比乙班多6×2=12人，也就知道了甲乙两班的人数之差是12，又因为题目中告诉我们甲乙两个班的学生共有84人，可以知道甲班有（84+12）÷2=48人，乙班的人数是48-12=36人。
3、整理解题思路学生叙述解题过程【思路点拨】如上图所示，根据“如果从甲班调6人到乙班，则两班人数相等”可以推出，甲班比乙班多6×2=12人，即甲、乙两班的人数之差是12，由“甲、乙两班共有学生84人”可以知道甲、乙两班的人数之和是84，根据和差问题的关系式即可以求出两个班原来各有学生多少人。
【解答】甲、乙两班的人数之差：6×2=12（人）甲班的人数：（84+12）÷2=48（人）乙班的人数：48-12=36（人）答：原来的甲班有学生48人，乙班有学生36人。
例2 把一根长100米的绳子剪成3段，要求第二段比第一段多16米，第三段比第一段少18米，三段绳子各应长多少米？1、题意理解根据题意，可以通过用画线段图的方法来题目中的已知条件和未知条件很清晰的反映出来，这种解题思想需要让学生学会，并且运用到平时的解题中。
(完整版)和差问题教案
和差问题教案教学目标1. 会判断什么样的应用题属于和差问题． 已知两个数的和以及两个数的差， 要分别求这 两个数就属和差问题，并掌握和差问题的特性，为以后继续学习和倍、差倍问题做准备．2. 总结归纳出解决和差问题的方法，并解决一些实际问题．基本概念 ：已知几个数的和与差，求这几个数的应用题，叫和差问题。
基本思路 ：通常采用假设的方法， 就是假设那个较小的数和较大的数相等或者假设那个较大 的数和那个较小的数相等，这样就会引起总数（和）的变化（增加或减少） ，求出新的和， 平均分就可得其中的一个数。
为了解答这种应用题， 首先要弄清两个数相差多少的不同叙述 方式 .有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗 藏的差叫“暗差” 。
关键问题 ：求出同一条件下的和与差。
较小数 +差=较大数 和-较小数 =较大数 较大数 -差=较小数 和-较大数 =较小数知识点拨： 和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题。
例 1：两筐水果共重 150 千克，第一筐比第二筐少 10 千克，两筐水果各多少千克？ 1、 读题，找出条件和问题。
2、 根据条件和问题画出线段图3、 想一想假设两筐的水果一样重好求吗？（总重量÷ 2）4、 假设把第二筐多的 10 千克减掉，看成两个第一筐的重量来计算，总重量要变成多 少？怎么计算？列式：第一筐： （150 10） 2 70 （千克）第二筐： 70 10 80（千克）5、 假设把第一筐少的 10 千克补上，看成两个第二筐的重量来计算，总重量要变成多 少？怎么计算？列式：第二筐： （150 10） 2 80 （千克）第一筐： 80 10 70 （千克）6、小结：知道两个数的和，以及它们的差，要求这两个数，解决和差问题需要我们画 线段图来分析，方法如下：方法一： （ 和+差） ÷2=大数和-大数 =小数 方法二： （ 和-差） ÷2=小数 和-小数 =大数基本公式 ：①（和 - 差）÷ 2=较小数②（和 +差）÷ 2=较大数巩固练习：（ 1）甲、乙两人同时以相同的速度打字， 2分钟共打了 240 个字，已知甲每分钟比乙多打 10 个字．问甲、乙两人每分钟各打多少个？ 问：题目中知道了什么条件？ 问：“已知甲每分钟比乙多打 10 个字”这个条件告诉我们甲、 乙两人每分钟打字的什么？ 问：根据“ 2 分钟共打了 240个字”可以求出什么？ （甲、 乙两人一分钟就打了 240 2 120 （个））师：这实际上就知道了甲、 乙两人每分钟打字的和， 这样就转换成典型和差问题了．方法一：甲： （240 2 10） 2 65（ 个）乙： 65 10 55（个）方法二：乙： （240 2 10） 2 55（ 个）甲： 55 10 65 （个）在研究完这两种方法以后， 老师要注意引导学生来总结和差问题的解决方法． 解答明差问题钢笔的价钱：？元 10 元自动铅笔的价格：？元 6 元 解法一：假设铅笔与钢笔价钱相同（假设都是钢笔） ，买一支钢笔、一支铅笔共花 10+6=16 （元），这是两支钢笔的钱。
《和差问题》教学设计
《和差问题》教学设计和差问题教学设计1. 设计目标本教学设计的目标是引导学生理解和应用和差问题的概念与解决方法，通过实际问题的探索，培养学生的逻辑思维、数学思维和解决问题的能力。
2. 教学准备2.1 教学资源- 教科书：包含和差问题相关内容的数学教材- 录像或图片：用于展示实际问题- 白板和黑板笔- 小道具：如计算器、图示材料等2.2 教学环境- 教室：可以容纳学生进行小组活动和讨论2.3 学生准备- 学生预：要求学生在课前阅读与和差问题相关的教材内容，了解基本概念和解题方法3. 教学过程3.1 导入环节学生入座后，教师可以提出一个简单的问题来引起学生的思考，例如：> 小明手里有5个苹果，小红给了他3个苹果，那么小明一共有几个苹果？学生可以就此问题进行讨论和思考，并尝试给出自己的答案。
然后教师可以请学生归纳总结这个问题背后的数学思想。
3.2 概念讲解在导入环节之后，教师可以引出和差问题的概念，解释和差问题是指在某个数值增加或减少的基础上进行计算的一类问题。
教师可以使用教材提供的定义和实例来帮助学生理解。
3.3 实例探索教师可以展示一些实际生活中的和差问题，如购物消费、人口增长等，激发学生的兴趣和思考。
学生可以在小组内讨论解决这些问题的方法，并展示他们的思路和计算过程。
3.4 教学拓展在学生对和差问题的概念有了初步理解后，教师可以引导学生进行更深入的思考和探索。
教师可以给出一些更复杂的和差问题，要求学生根据自己的理解和所学的解决方法，独立解决这些问题。
3.5 总结与评价课堂结束前，教师可以对学生的解决方法进行总结和评价。
教师可以鼓励学生将解题思路和方法分享给其他同学，并提供一些额外的练题，供学生在课后巩固研究。
4. 研究评估为了评估学生对和差问题的掌握程度，教师可以设计一些小测验或练题，要求学生独立完成。
通过评估学生的答题情况，教师可以了解学生的研究进展，并对教学内容进行调整和改进。
5. 参考资源- [教材名称1]- [教材名称2]- [教材名称3]以上为《和差问题》教学设计的基本框架，教师可以根据实际情况进行适当调整和拓展，帮助学生更好地理解和应用和差问题的知识。
(完整版)和差问题(一)教案
和差问题第一讲一、兴趣导入 (Topic-in):兴趣分享麒麟飞到北极变什么啊？答案：冰激凌世界上什么鸡跑的快？答案：肯德鸡块一片大草地（植物）答案：梅花（没花）又一片大草地（植物）答案：野梅花来了一群羊（水果）答案：草莓来了一群狼（水果）答案：杨梅来了一群狮子（体坛名将）答案：郎平什么动物最没有方向感？答案：麋鹿（迷路）二、学前测试 (Testing):问答题（口答）1、鸡兔同笼问题的公式？三、知识解说 (Teaching) ：基础知识说到“和差问题”，小学高年级的同学，人人都会说：“我会！”和差问题的计算太简单了.是的，知道两个数的和与差，求两数，有计算公式：大数 =（和 +差）÷ 2小数 =（和 - 差）÷ 2会算，还要会灵巧运用，要把某些应用题转变为和差问题来算.先看几个简单的例子 .例 1 张明在期末考试时，语文、数学两门功课的均匀得分是 95 分，数学比语文多得 8 分，张明这两门功课的成绩各是多少分？解： 95 乘以 2，就是数学与语文两门得分之和，又知道数学与语文得分之差是8.所以数学得分 =（95×2＋8）÷ 2＝99.语文得分 =(95 × 2-8 ）÷ 2＝ 91.答：张明数学得99 分，语文得 91 分.注：也能够从 95 ×2-99 ＝91 求出语文得分 .例 3、两筐水果共重 150 千克，第一筐比第二筐少10 千克，两筐水果各多少千克？例 2 有 A，B，C 三个数， A加 B 等于 252 ，B加 C 等于 197 ， C 加 A 等于 149 ，求这三个数.解：从 B+C＝197 与 A+C＝149，就知道 B与 A 的差是 197-149 ，题目又告诉我们，B 与 A 之和是 252. 所以B=（ 252＋ 197-149 ）÷ 2 ＝ 150 ，A＝252-150 ＝102，C＝149-102 ＝47.答： A， B， C 三数分别是 102，150，47.注：还有一种更简单的方法（A+B）＋（ B＋ C）＋（ C＋A）＝ 2×（ A＋B＋C）.上边式子说明，三数相加再除以2，就是三数之和 .A＋B＋C＝（ 252＋ 197＋149）÷ 2＝ 299. 所以C＝299-252 ＝47，B＝299-149 ＝150，A＝299-197 ＝102.例 3 甲、乙两筐共装苹果 75 千克，从甲筐取出 5 千克苹果放入乙筐里，甲筐苹果还比乙筐多 7 千克 . 甲、乙两筐原各有苹果多少千克？解：画一张简单的表示图，就能够看出，本来甲筐苹果比乙筐多5＋7＋ 5 ＝ 17 （千克）所以，甲、乙两数之和是75 ，差为 17.甲筐苹果数 =（ 75＋17）÷ 2＝ 46 （千克） .乙筐苹果数 =75-46 ＝29（千克） .答：本来甲筐有苹果46 千克，乙筐有苹果29 千克 .例 3、长方形操场的长与宽相差 80 米，沿操场跑一周是 400 米，求这个操场的长与宽是多少米？【分析】长方形一周的长是指两条长和两条宽的和，由条件可知一条长与一条宽的和为400 2 200 (米)，由此我们就知道了长和宽之和是200 米，又知道长和宽之差是80 米，依据和差问题来解答：方法一：长：（20080） 2140 (米)宽： 1408060（米）方法二：宽：（20080） 260(米)长： 6080140（米）例 4 张强用 270 元买了一件外套，一顶帽子和一双鞋子 . 外套比鞋贵 140 元，买外套和鞋比帽子多花 210 元，张强买这双鞋花多少钱？解：我们先把外套和鞋当作一件东西，它与帽子的价钱和是270 元，差是 210 元 .外套和鞋价之和 =（270＋ 210 ）÷ 2＝ 240 （元） .外套价与鞋价之差是140，所以鞋价 =（ 240-140 ）÷ 2＝50（元） .答：买这双鞋花50 元 .四、加强练习 (Training)：1、甲、乙两人同时以相同的速度打字，2分钟共打了240个字，已知甲每分钟比乙多打 10 个字．问甲、乙两人每分钟各打多少个？2、甲乙两筐水果共 40 千克，假如从甲筐那 6 千克放入乙筐，甲的就比乙的多 2 千克。
四年级数学下册《和差问题》教案、教学设计
-加强与家长的沟通，了解学生的课外学习情况，为学生的数学学习提供全方位的支持。
-组织课后辅导和拓展活动，针对学习困难的学生进行个别辅导，提高整体教学效果。
四、教学内容与过程
（一）导入新课
1.教学活动设计：
-利用多媒体展示小明和小华一起在超市购物的情境，提出问题：“小明和小华一共买了多少钱的东西？小明比小华多花了多少钱？”引导学生关注和差问题。
（二）过程与方法
在本章节的教学过程中，教师应注重以下过程与方法：
1.采用情境教学法，创设生活情境，让学生在实际问题中发现和差问题，激发学生学习兴趣。
2.引导学生通过观察、分析、归纳等思维活动，发现和差问题的规律，培养学生解决问题的能力。
3.教学中注重师生互动，引导学生主动探究，发挥学生的主体作用。
4.设计不同难度的练习题，使学生在分层练习中逐步提高，培养其独立思考和解决问题的能力。
-通过这个生活实例，让学生感受到数学与生活的紧密联系，激发学生学习兴趣。
2.教学过程：
-学生观看多媒体展示，教师引导学生关注和差问题。
-学生回答问题，教师总结和差问题的特点，为新课的学习做好铺垫。
（二）讲授新知
1.教学活动设计：
-教师通过具体例题，讲解和差问题的解题思路和方法。
-引导学生从实际问题中抽象出和差问题，学会用数学语言描述问题，列出相应的算式。
-针对共性问题，教师进行讲解，帮助学生理解和掌握。
（五）总结归纳
1.教学活动设计：
-教师引导学生回顾本节课所学内容，总结和差问题的解题方法和技巧。
-学生分享学习心得，交流在学习过程中遇到的困难和解决方法。
和差教学设计
和差教学设计第1篇：和差问题的教学设计《和差问题》的教学设计【设计理念】数学课程标准指出：学生的数学学习内容应当是现实的、有意义的、富有挑战性的；学生的学习方式应以动手操作、自主探索、合作交流为主；数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础上。
本节课创设储蓄罐的教学情境，吸引学生参与。
在教学过程中，注重培养学生的探究意识、小组合作意识。
让学生通过动手操作亲身经历知识形成过程，促进学生主动学习。
【教学内容】和差问题【教学目的】a、通过直观演示的教学，让学生理解和差问题的特点及其解题思路，学会解决身边的数学问题。
b、了解数学在现实生活中的作用，体会学习数学的重要性.c、通过合作探究，让学生知道用不同的方法解决同一个问题，进而提高解决问题的能力；培养学生全面解决问题的习惯和灵活解决问题的能力，培养学生与他人相互交流，合作的意识。
【教学重点】让学生通过直观演示，合作探究，掌握和差问题的特点及其解题思路。
【教学难点】理解和差问题的解题思路【教具准备】两根长短不同的纸条、小黑板【教学过程】一、创设情境，导入新课同学们：看看老师今天给大家带来了什么（储蓄罐）看到它你们想说什么你家有吗它有什么用途你能告诉老师你存了多少钱吗你攒的这些钱用来做什么呢学情预设：学生可能会提出：1：我用这些钱买学习用品。
2：我用这些钱给妈妈买生日礼物。
3：我把这些钱捐给灾区上不起学的学生。
师：同学们都是好样的﹗能自己攒钱做有意义的事情，老师为你们而骄傲。
设计意图：创设储蓄罐的教学情境，使学生感受数学与生活的联系，同时渗透从小要有节约的意识，要有爱心的思想品德教育。
老师也带来了两位小朋友储蓄的钱：小花18元，小明20元。
师：看到这两个信息，你们想说什么学情预设：学生可能会提出：1、他们一共存了多少钱2、小花比小明少存了多少钱3、小花再存多少钱就和小明一样多了4、小明给小花多少钱两人就同样多了师：你们说得真好！这些问题怎样解决呢各求的是什么量呢怎么求呢谁能帮他们解决学情预设：学生可能会提出：和是38，差是2。
2023-2024学年四年级下学期数学8.2和差问题(教案)
20232024学年四年级下学期数学8.2和差问题（教案）作为一名经验丰富的教师，我将以我的口吻来写这份教案，确保内容丰富且具有实践性。
一、教学内容本节课的教学内容选自四年级下学期数学教材第八章，主要讲述和差问题。
具体内容包括理解并掌握和差问题的概念，学会用加减法解决和差问题，并能够应用到实际情境中。
二、教学目标通过本节课的学习，我希望学生能够：1. 理解并掌握和差问题的解法；2. 能够应用和差问题解决实际问题；3. 培养学生的逻辑思维能力和解决问题的能力。
三、教学难点与重点本节课的重点是让学生掌握和差问题的解法，并能应用到实际情境中。
难点是理解和掌握和差问题的概念。
四、教具与学具准备为了更好地进行课堂教学，我准备了PPT、黑板、粉笔、练习题等教具和学具。
五、教学过程1. 实践情景引入：我将以一个生活中的实际问题引入本节课，例如：“小明有5个苹果，小红的苹果比小明多3个，小华比小红少2个，请问小华有几个苹果？”让学生思考并解答。
2. 讲解和差问题的概念：在学生解答完实际问题后，我会引导学生思考和差问题的定义，即两个数的和与差的关系。
3. 例题讲解：我会选取一些典型的和差问题进行讲解，让学生通过观察和操作，理解并掌握和差问题的解法。
4. 随堂练习：在讲解完例题后，我会设计一些随堂练习题，让学生即时巩固所学知识。
5. 应用拓展：我会设计一些实际问题，让学生运用和差问题的解法进行解决，培养学生的应用能力。
六、板书设计板书设计将简洁明了，突出和差问题的解法步骤，包括：1. 理解题意；2. 列出算式；3. 计算结果；4. 检验答案。
七、作业设计作业设计将包括一些和差问题的练习题，让学生在课后巩固所学知识。
具体的作业题目和答案如下：1. 小明有8个苹果，小红的苹果比小明多6个，小华比小红少4个，请问小华有几个苹果？答案：小华有10个苹果。
2. 小刚有7个橘子，小丽的橘子比小刚少5个，小芳比小丽多3个，请问小芳有几个橘子？答案：小芳有5个橘子。
四年级《和差问题》奥数教案
米德和欧拉在超市一共买了246元的零食，欧拉比米德少买12元。两人各买了多少钱的零食？
【课件出示例题一。】
师：同学们，请先认真地读一读这道题，然后再找一找这道题中已经给出的已知信息。
生1：米德和欧拉一共买了246元的零食。
师：也就是说，题中给我们的一个已知信息是两人所买零食的总价是246元对吧。很好，请坐。还有其他已知信息吗？
生：258元。
师：很好。那么，总价钱算出来之后，现在我们能求出其中一个人所花的钱数吗？
生：可以，可以求出米德所花的钱。
师：怎么求？
生：用258除以2。
师：为什么这么求？
生：因为总钱数变了之后，是米德钱数的两倍。
师：没错，你发现了一个特别重要的信息。不知道其他同学发现没有？
生：发现了。
师：恩，真厉害。直接看图，我们可以发现这两条线段的长度相等，而这线段的长度所表示的是米德所花的钱数。所以，我们就可以用总价钱除以2，就可以求得米德所花的钱数了。那么，我们既然可以求出米德所花的钱数，欧拉的也就很容易求的出来了，对吧？
生：可以。
师：很好。那么，根据这个，你们有什么办法可以求出两人分别花了多少钱吗？
师：来，我对这个示意图再做个小变动，你们就可以容易想的到了。请看，说说发现了什么。
生：增加虚线之后，两个线段一样长了。
师：说得真棒，那你知道，这条虚线表示多少钱吗？
生：表示12元钱。
师：为什么？
生：因为欧拉花的钱比米德花的要少12元，只有再加上12元，才会跟米德的钱一样多。
师：那现在，我们知道了两数差是10，还知道了两数和是90。那我们就可以利用和差问题来解决这道题了。
师：那又该怎么解答呢？
生：用90减去10再除以2。
和差问题(教学设计)北师大版三年级上册数学
和差问题教学设计（北师大版三年级上册数学）一、教学目标1.知识与技能目标1.掌握两个数的和及差的概念。
2.掌握进行加法和减法运算的基本方法。
3.能够利用两个数的和及差解决实际问题。
2.过程与方法目标1.培养学生的数学思维能力及运算能力。
2.能够理解数学知识在解决实际问题中的应用。
二、教学重点1.掌握两个数的和的概念。
2.掌握进行加法运算的基本方法。
3.掌握应用两个数的和解决实际问题。
三、教学难点1.理解两个数之间相互转换的概念。
2.掌握两个数的差的概念。
3.理解减法运算的原理和方法。
四、教学步骤1.前置知识概括回顾1.回顾加法运算的基本方法。
2.提问：两个数之间有哪些关系？答：两个数之间有几个不同的关系，包括大小顺序、相等、和、差等关系。
2.引入新知识1.板书：“两个数的和是指将两个数相加所得到的一个新数。
”2.板书：“两个数的差是指两个数之间的距离。
”3.板书示例：“3 + 4 = 7 , 7 - 4 = 3 , 7 - 3 = 4”3.教学重点讲解1.掌握两个数的和的概念。
2.掌握进行加法运算的基本方法。
4.教学目标实现1.练习加法运算，掌握其基本方法。
2.通过实例演示加法运算，引导学生掌握两个数的和的概念。
5.教学难点解决1.体验两个数之间转换的过程，理解两个数之间相互转换的概念。
2.理解减法运算的原理和方法。
五、教学评价在教学中，应注意以下的评价措施：1.评估学生的加法及减法运算能力。
2.评估学生应用两个数的和及差解决实际问题的能力。
3.评估学生掌握两个数之间相互转换的能力。
六、教学反思在这次教学中，我认为我做得比较好的地方是：1.通过实例演示，引导学生掌握加法运算。
2.培养学生数学思维能力。
需要改进的地方：1.应加强学生对两个数之间相互转换的理解和掌握。
2.应加强学生在实际问题中应用数学知识的能力。
和差问题1学案
和差问题1学案第一篇：和差问题1学案教育是一项良心工程！学案例1：两筐水果共重150千克，第一筐比第二筐多8千克，两筐水果各多少千克？▲观察题目，联系前两次所学内容，请说说题目中已知条件及所求问题。
☆尝试概括：我们今天要学习的内容是什么？分析与解答：我们可以这样想：假设第二筐和第一筐重量相等时，两筐共重150＋8＝158（千克）；假设第一筐重量和第二筐相等时，两筐共重150-8＝142（千克）.解法1：①第二筐重多少千克？（150-8）÷2=71（千克）②第一筐重多少千克？71＋8=79（千克）或 150-71=79（千克）解法2：①第一筐重多少千克？（150+8）÷2＝79（千克）②第二筐重多少千克？79-8=71（千克）或150-79=71（千克）答：第一筐重79千克，第二筐重71千克。
1-1学校有排球、篮球共62个，排球比篮球多12个，排球、篮球各是多少个？1-2甲、乙两人的年龄和是35岁，甲比乙小5岁，甲、乙各多少岁？例2：今年小强7岁，爸爸35岁，当两人年龄和是58岁时，两人年龄各多少岁？分析与解答：题中没有给出小强和爸爸年龄之差，但是已知两人今年的年龄，那么今年两人的年龄差是35-7=28（岁）.不论过多少年，两人的年龄差是保持不变的.所以，当两人年龄和为58岁时他们年龄差仍是28岁.根据和差问题的解题思路就能解此题。
欣赏您的孩子，其实天才就在你身边！教育是一项良心工程！2-1今年小刚和小强两人年龄和为22岁，一年前，小刚比小强大四岁，今年小刚和小强各是多少岁？例3 ：小明期末考试时语文和数学的平均分数是94分，数学比语文多8分，问语文和数学各得了几分？分析与解答：解和差问题的关键就是求得和与差，这道题中数学与语文成绩之差是8分，但是数学和语文成绩之和没有直接告诉我们.可是，条件中给出了两科的平均成绩是94分，这就可以求得这两科的总成绩.答：小明期末考试语文得分，数学得分.3-1小敏与妈妈今年的平均年龄为20岁，三年后，妈妈比小敏大28岁，今年妈妈和小敏各是多少岁？★知识点拨：和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的应用题。
和差问题教案-
和差问题教案教学目标1.教学生会判断什么样的问题属于和差问题．已知两个数的和以及两个数的差，要分别求这两个数就属和差问题，利用线段图理解并掌握和差问题的特性，为以后继续学习和倍、差倍问题做准备．2.通过线段图总结归纳出解决和差问题的方法，并解决一些实际问题．基本概念：已知几个数的和与差，求这几个数的问题，叫和差问题。
基本思路：通常采用假设的方法，就是假设那个较小的数和较大的数相等或者假设那个较大的数和那个较小的数相等，这样就会引起总数（和）的变化（增加或减少），求出新的和，平均分就可得其中的一个数。
为了解答这种问题，首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差，而有些问题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”。
关键问题：求出同一条件下的和与差。
基本公式：①（和-差）÷2=较小数较小数+差=较大数和-较小数=较大数②（和+差）÷2=较大数较大数-差=较小数和-较大数=较小数知识点拨：和差问题是已知大小两个数的和与这两个数的差，求大小两个数各是多少的问题。
教学过程：一、知识铺垫，激趣导入1、出示课件图，同学们好，老师今天给你们带来了一件神秘的礼物，听着这个音乐，猜猜会是什么呢？（放音乐，展示圣诞树）你真聪明！是一棵美丽圣诞树，同学们，圣诞树还带来了一件能让你变得更聪明的智慧礼物，想得到吗？可是，要先回答它的两个问题哦！你们有信心吗？听，圣诞树说，小朋友，你们能找到我身上的数学信息吗？学生们能过观察很快找到（有4颗黄色星星，少；有7颗红色星星，多；一共有11颗）2、说得太好了！再回答一个问题就能知道智慧礼物是什么了。
你有办法让两种星星的数量变得一样多吗？想好了吗，谁来说说你办法？（这时候，学生会想到两种方法）方法一：去多。
把红色星星减少3颗，变成4颗，和黄色星星一样多了。
而它们的总和呢？（减少了3颗，变成了2个4，也就是8颗）方法二：补少。
给黄色星星增加3颗，变成7颗，就和红色星星一样多了。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
和差问题第一讲一、兴趣导入(Topic-in):趣味分享麒麟飞到北极变什么啊？答案：冰激凌世界上什么鸡跑的快？答案：肯德鸡块一片大草地（植物）答案：梅花（没花）又一片大草地（植物）答案：野梅花来了一群羊（水果）答案：草莓来了一群狼（水果）答案：杨梅来了一群狮子（体坛名将）答案：郎平什么动物最没有方向感？答案：麋鹿（迷路）二、学前测试(Testing):问答题（口答）1、鸡兔同笼问题的公式？三、知识讲解(Teaching)：基础知识说到“和差问题”，小学高年级的同学，人人都会说：“我会！”和差问题的计算太简单了.是的，知道两个数的和与差，求两数，有计算公式：大数=（和+差）÷2小数=（和-差）÷2会算，还要会灵活运用，要把某些应用题转化成和差问题来算.先看几个简单的例子.例1 张明在期末考试时，语文、数学两门功课的平均得分是95分，数学比语文多得8分，张明这两门功课的成绩各是多少分？解：95乘以2，就是数学与语文两门得分之和，又知道数学与语文得分之差是8.因此数学得分=（95×2＋8）÷2＝99.语文得分=(95×2-8）÷2＝ 91.答：张明数学得99分，语文得91分.注：也可以从 95×2-99＝91求出语文得分.例3、两筐水果共重150千克，第一筐比第二筐少10千克，两筐水果各多少千克？例2 有 A，B，C三个数，A加 B等于 252，B加 C等于 197， C加 A等于 149，求这三个数.解：从B+C＝197与A+C＝149，就知道B与A的差是197-149，题目又告诉我们，B与A之和是252.因此B=（252＋ 197-149）÷ 2＝ 150，A＝252-150＝102，C＝149-102＝47.答：A，B，C三数分别是102，150，47.注：还有一种更简单的方法（A+B）＋（B＋C）＋（C＋A）＝2×（A＋B＋C）.上面式子说明，三数相加再除以2，就是三数之和.A＋B＋C＝（252＋197＋149）÷2＝299.因此C＝299-252＝47，B＝299-149＝150，A＝299-197＝102.例3甲、乙两筐共装苹果75千克，从甲筐取出5千克苹果放入乙筐里，甲筐苹果还比乙筐多7千克.甲、乙两筐原各有苹果多少千克？解：画一张简单的示意图，就可以看出，原来甲筐苹果比乙筐多5＋7＋ 5＝ 17（千克）因此，甲、乙两数之和是 75，差为17.甲筐苹果数=（75＋17）÷2＝ 46（千克）.乙筐苹果数=75-46＝29（千克）.答：原来甲筐有苹果46千克，乙筐有苹果29千克.例3、长方形操场的长与宽相差80米，沿操场跑一周是400米，求这个操场的长与宽是多少米？【解析】长方形一周的长是指两条长和两条宽的和，由条件可知一条长与一条宽的和为÷= (米)，由此我们就知道了长和宽之和是200米，又知道长和宽之差是400220080米，根据和差问题来解答：方法一：长：200802140-=（米）+÷=（） (米) 宽：1408060方法二：宽：20080260-÷=+=（米）（） (米) 长：6080140例4张强用270元买了一件外衣，一顶帽子和一双鞋子.外衣比鞋贵140元，买外衣和鞋比帽子多花210元，张强买这双鞋花多少钱？解：我们先把外衣和鞋看成一件东西，它与帽子的价格和是 270元，差是 210元.外衣和鞋价之和=（270＋ 210）÷2＝ 240（元）.外衣价与鞋价之差是140，因此鞋价=（240-140）÷2＝50（元）.答：买这双鞋花50元.四、强化练习(Training)：1、甲、乙两人同时以相同的速度打字，2分钟共打了240个字，已知甲每分钟比乙多打10个字．问甲、乙两人每分钟各打多少个？2、甲乙两筐水果共40千克，如果从甲筐那6千克放入乙筐，甲的就比乙的多2千克。
两筐原来有多少水果？五、训练辅导(Tutor):1、图书馆的书架上、下两层共存书220本，如果从上层拿出10本放入下层，则两层书架上书数相等．求原来上、下层各存书多少本？方法一：下层：220202100（） (本) 上层：220100120-= (本)-÷=方法二：上层：220202120-=（本）+÷=（）（本）下层：2201201002、商店里每天卖出电脑10台，卖出的彩电比电脑多5台，一个星期商店卖出电脑和彩电一共多少台？【解析】方法一：每天卖出电脑和彩电多少台？1051025++=（台）一个星期商店卖出电脑和彩电一共多少台？257175⨯=（台）方法二：电脑一个星期共卖出多少台？10770⨯=（台）彩电一个星期共卖出多少台？1057105（）（台）+⨯=一个星期商店卖出电脑和彩电一共多少台？70105175+=（台）答：一个星期商店卖出电脑和彩电一共175台六、反思总结(Thinking)：课堂训练（总分100分）1、两个连续奇数的和是36，这两个数分别是多少？两个连续奇数的差是2,利用和差公式解答如下．较小数：36-2217-=（）较大数：361719÷=2、小勇家养的白兔和黑兔一共有22只，如果再买4只白兔，白兔和黑兔的只数一样多．小勇家养的白兔和黑兔各多少只？方法一：把黑兔多的4只减掉，看成两个白兔的数量来计算．列式：白兔：22429-= (只) 或9413+= (只)（）（只），黑兔：22913-÷=方法二：把白兔少的4只加上，看成两个黑兔的数量来计算．列式：黑兔：224213-= (只) 或1349-=(只)（） (只) ，白兔：22139+÷=3、学校水果店运来苹果和梨共40千克，苹果比梨多2袋，苹果和梨每袋都重5千克，则水果店运来苹果和梨各多少袋？方法一：题目中知道了苹果比梨多2袋，如果能求出苹果和梨一共的袋数，就可以用和差问题来解决了．而题目中只告诉我们苹果和梨共40千克，不过还告诉我们苹果和梨每袋都重5千克，那么就可以求出苹果和梨一共有4058÷=（袋），现在就可以求出梨有8223（）（袋）．-÷=+÷=（）（袋），苹果有82254、周明和王刚两人数学成绩的和是182分．周明如果多考5分，就比王刚多3分．周明和王刚的数学各考了多少分？【解析】已知周明和王刚两人数学成绩的和是182分，根据条件“周明如果多考5分，就比王刚多3分“可知，王刚的数学成绩比周明多532-=（分）．转换成和差问题解答如下：方法一：王刚：1822292（）（分）周明：92290-=（分）+÷=方法二：周明：1822290+=（分）（）（分）王刚：90292-÷=5、甲、乙两校共有学生1050人，部分学生因搬家需要转学，已知由甲校转入乙校20人，这样甲校比乙校还多10人，求两校原来有学生多少人？【解析】这道题虽然只告诉了我们两个数的和，但是两数的差属于隐藏条件．由甲校转入乙校20人，这样甲校比乙校还多10人，实际上甲校比乙校多2021050⨯+= (人)，找到了隐藏的差，就转变成了典型的和差问题．列式：乙：1050502500-= (人（） (人) 甲：1050500550-÷=家庭作业（总分100分）1、果园共260棵桃树和梨树，其中桃树的棵数比梨树多20棵．桃树和梨树各有多少棵？【解析】方法一：桃树：260202140（）（棵）梨树：14020120-=（棵）+÷=方法二：梨树：260202120+=（棵）（）（棵）桃树：12020140-÷=答：桃树有140棵，梨树有120棵．2、有一根钢管长12米，要锯成两段，使第一段比第二段短2米．每段各长多少米？【解析】第一段：12225-÷=-= (米)（） (米) 第二段：1257答：第一段长5米，第二段长7米．3、丁丁在期中考试时，语文、数学两科平均分是91分，数学比语文多2分，那么丁丁语文和数学各得了多少分？【解析】在这道题中，我们已知丁丁数学成绩比语文成绩多2分，也就是知道了数学成绩和语文成绩之差，如果找到数学成绩和语文成绩之和，就转换成和差问题来解答了．又因为知道了语文和数学的平均分是91分，那么两科成绩之和就是912182⨯=（分）．方法一：数学：1822292-=（分）（）（分）语文：92290+÷=方法二：语文：1822290-÷=+=（分）（）（分）语文：902924、小华和小敏共有铅笔25枝，如果小华用去4枝，小敏用去3枝，那么小华还比小敏多2枝，小华和小敏原来各有多少枝铅笔？【解析】如果小华用去4枝，小敏用去3枝，那么小华还比小敏多2枝，这就说明原来小华的铅笔比小敏的铅笔多3枝．找到了这个暗差，这道题就简单了．方法一：小华：253214-=（枝）（）（枝）小敏：14311+÷=方法二：小敏：253211+=（枝）（）（枝）小华：11314-÷=5、有大、小两个油桶，一共装油24千克，两个油桶都倒出同样多的油后分别还剩9千克和5千克．问：原来大、小两个油桶各装油多少千克？【解析】两个油桶都倒出同样多的油后分别还剩9千克和5千克，那么也就是说大桶比小桶多4千克的油，知道这两桶油的和，又找到了这两桶油的差，这道题就变成了典型的和差问题的应用题了．方法一：大桶：244214-=（千克）（）（千克）小桶：14410+÷=方法二：小桶：244210+=（千克）（）（千克）大桶：10414-÷=。