七年级数学应用与创新竞赛试题及答案201321
七年级数学竞赛试题及答案

七年级数学竞赛试题一、选择题(每小题4分,共40分)1、如果m 是大于1的偶数,那么m 一定小于它的……………………( )A 、相反数B 、倒数C 、绝对值D 、平方2、当x=-2时, 37ax bx +-的值为9,则当x=2时,37ax bx +-的值是 ( )A 、-23B 、-17C 、23D 、173、255,344,533,622这四个数中最小的数是………………………( )A. 255B. 344C. 533D. 6224、把14个棱长为1的正方体,在地面上堆叠成如图1所示的立体,然后将露出的表面部分染成红色.那么红色部分的面积为 …………………………….. ( ).A 、21B 、24C 、33D 、37 5、有理数的大小关系如图2所示,则下列式子中一定成立的是……( ) A 、c b a ++>0 B 、c b a <+ C 、c a c a +=- D 、a c c b ->-6、某商场国庆期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100元(100元可以是现金,也可以是购物券,或二者合计)就送20元购物券,满200元就送40元购物券,依次类推,现有一位顾客第一次就用了16000元购物,并用所得购物券继续购物,那么他购回的商品大约相当于打 ( )A 、9折B 、8.5折C 、8折D 、7.5折7、如果有2005名学生排成一列,按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数,那么第2005名学生所报的数是……………………………………………………………… ( )A 、1B 、2C 、3D 、48、方程 |x|=ax+1有一负根而无正根, 则a 的取值范围…………( )A. a>-1B. a>1C. a ≥-1D. a ≥19、122-+-++x x x 的最小值是…………………………………( )A. 5B.4C.3D. 210、某动物园有老虎和狮子,老虎的数量是狮子的2倍。
七年级数学应用与创新竞赛试题及答案

第1页 共6页七年级数学应用与创新竞赛试题(时间:120分钟,满分:100分)一、填空题(每小题5分,共40分)1.已知a =1999x +2000,b =1999x +2001,c =1999x +2002,则多项式a 2+b 2+c 2-ab -bc -ca 的值为 2.关于x,y 的方程xy=x+y 的整数解有_____组.3.用[]x 表示不大于x 的最大整数,如果[]3x =-,那么x 的取值范围是 4.正五边形广场ABCDE 的周长为2000米.甲、乙两人分别从A 、C 两点同时出发,沿A →B →C →D →E →A →…方向绕广场行走,甲的速度为50米/分,乙的速度为46米/分.那么出发后经过 分钟,甲、乙两人第一次行走在同一条边上...... 5.一质点在一直线上从A 点开始以每分钟2米的速度进行运动,其运动方式是:前进1米后退2米,前进3米后退4米,……,如此反复,当它第一次到达离A 点10米的B 点时要经过 分钟。
6. 10个人围成一个圆圈做游戏,游戏的规则是:每个人心 里都想好一个数,并把自己想好的数如实告诉两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报3的人心里想的数是 ;7.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸,•结果比平时早20分钟到家,则小林步行________分钟遇到来接他的爸爸. 8.如图,在Rt ΔABC 中,∠ACB=90°,∠ABC=62°,将ΔABC 绕顶点C 旋转到ΔA ´B ´C 的位置,使顶点B 恰好落在斜边A ´B ´上,设A ´C 与AB 相交于点D ,则∠BDC 的度数是二、选择题(每小题4分,共24分)45678910123第8题图第2页 共6页(1)(2)(3)9.如图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )(A )25 (B )66 (C )91 (D )12010.已知z y x ,,满足x z z y x +=-=532,则zy yx 25+-的值为( ) (A )1. (B )31. (C )31-. (D )21. 11.一只船有一个漏洞,水以均匀速度进入船内。
初中七年级上数学应用与创新竞赛试卷及答案
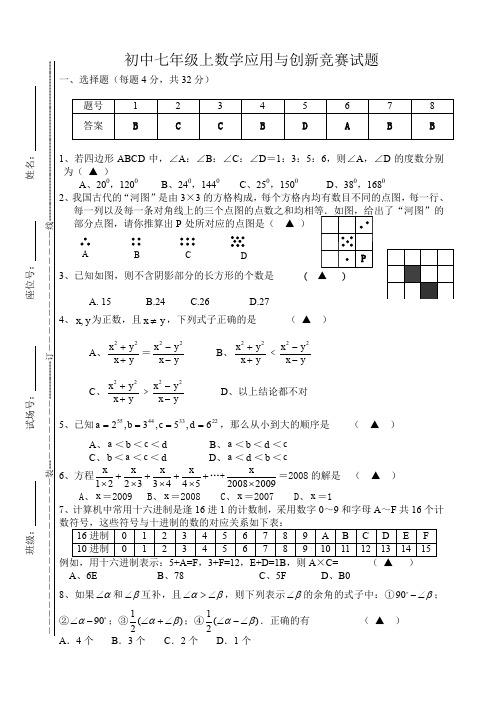
班级: 试场号: 座位号: 姓名:――――-―――――――――――――装---―――――――-------------订――――――――――――――线-------------------------------------------------------初中七年级上数学应用与创新竞赛试题一、选择题(每题4分,共32分)1、若四边形ABCD 中,∠A :∠B :∠C :∠D =1:3:5:6,则∠A ,∠D 的度数分别为( ▲ )A 、200,1200B 、240,1440C 、250,1500D 、380,1680 2、我国古代的“河图”是由3×3的方格构成,每个方格内均有数目不同的点图,每一行、部分点图,请你推算出P 处所对应的点图是( ▲ )3、已知如图,则不含阴影部分的长方形的个数是 ( ▲ )A. 15B.24C.26D.27 4、y x ,为正数,且y x ≠,下列式子正确的是 ( ▲ )A 、y x y x ++22=y x y x --22B 、y x y x ++22﹤y x y x --22C 、y x y x ++22﹥yx y x --22 D 、以上结论都不对5、已知223344556,5,3,2====d c b a ,那么从小到大的顺序是 ( ▲ )A 、a <b <c <dB 、a <b <d <cC 、b <a <c <dD 、a <d <b <c 6、方程+⨯+⨯+⨯+⨯54433221x x x x …+20092008⨯x=2008的解是 ( ▲ ) A 、x =2009 B 、x =2008 C 、x =2007 D 、x =17、计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共16个计A 、6E B 、78 C 、5F D 、B0 8、如果α∠和β∠互补,且αβ∠>∠,则下列表示β∠的余角的式子中:①90β-∠;②90α∠-;③1()2αβ∠+∠;④1()2αβ∠-∠.正确的有 ( ▲ )A B C D20cm30cm12cm 二、填空题(每题4分,共32分)1、已知3=a ,2=b ,且a b b a -=-,则b a += -1或 -52、012=-+m m ,则2009223++m m = 20103、老王想估计一下自己池塘里鱼的数量,第一天他捕上50条鱼做好标记,重新放回池塘,过了几天带标记的鱼完全混合于鱼群中,他又去捕捞了168条,发现做标记的鱼有8条,你帮老王估算一下池塘里的鱼为 1050 条。
初一数学创新试题及答案

初一数学创新试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于16,这个数可能是:A. 4B. -4C. 4和-4D. 以上都不是答案:C3. 一个长方形的长是宽的两倍,如果宽是a,那么面积是:A. 2a²B. 3a²C. 4a²D. 5a²答案:A4. 一个数的绝对值是它本身,这个数可能是:A. 正数B. 0C. 负数D. 正数或0答案:D5. 下列哪个选项是不等式3x - 5 > 10的解?A. x > 4B. x < 4C. x > 3D. x < 3答案:A二、填空题(每题2分,共10分)6. 圆的周长公式是________。
答案:C = 2πr7. 如果一个数的平方根是4,那么这个数是________。
答案:168. 一个数的倒数是1/5,这个数是________。
答案:59. 一个数的立方是27,这个数是________。
答案:310. 如果一个三角形的内角和为180°,那么一个直角三角形的两个锐角的和是________。
答案:90°三、解答题(共30分)11. 某班有40名学生,其中男生人数是女生人数的2倍。
求男生和女生各有多少人?答案:设女生人数为x,则男生人数为2x。
根据题意,x + 2x = 40,解得x = 40/3,但人数必须是整数,所以题目有误,无法求解。
12. 一个长方形的长是15厘米,宽是10厘米,求这个长方形的面积和周长。
答案:面积 = 长× 宽= 15 × 10 = 150平方厘米。
周长 = 2 × (长 + 宽) = 2 × (15 + 10) = 50厘米。
13. 一个数的3倍加上5等于这个数的5倍减去7,求这个数。
答案:设这个数为x,根据题意,3x + 5 = 5x - 7,解得2x = 12,所以x = 6。
衢江区2013年七年级数学应用与创新竞赛试题(含答案)

衢江区2013年七年级数学应用与创新竞赛试题(满分100分,考试时间:2013.2.23下午14∶00—16∶00)一、选择题(本题共有10小题,每小题4分,共40分,请选出一个正确的选项,将其代号填入题后的括号内,不选、多选、错选均不给分)1. 如果xy <0,且x >y ,则x +y 的值是( A )A. 正数B. 负数C. 非正数D. 零2. 若1528162m m ⨯⨯=,则m 的值为( B )A. 1B. 2C. 3D. 43. 若621x -表示一个整数,则整数x 可取的值共有( B ) A. 8个 B. 4个 C. 3个 D. 2个4. 已知2(1)()3x x a x bx -+=+-,则a +b 的值是( C )A. 1B. -1C. 5D. -55. 衢州市对迎宾大道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等. 如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完. 设原有树苗x 棵,则根据题意列出方程正确的是( A )A.5(211)6(1)x x +-=-B.5(21)6(1)x x +=-C. 5(211)6x x +-=D. 5(21)6x x +=6. 若2214a b -=,12a b -=,则b a 的值为( C ) A. 12- B. 12C. 1D. 0 7. 记248256(12)(12)(12)(12)(12)x =+++++ ,则x +1是( C )A.一个奇数B. 一个质数C. 一个整数的平方D. 一个整数的立方8. 从11111124681012+++++中删去两上加数后使余下的四个加数之和恰好等于1,那么删去的两个加数是( D ) A.14,16 B. 14,112 C. 16,110 D. 18,110 9. 如图,点A 、B 对应的数是a 、b ,点A 在-3,-2对应的两点(包括这两点)之间移动,B A b a 0-1-2-3(第9题图)16151413121110987654321…… (第1个正方形) (第2个正方形) (第3个正方形) (第4个正方形)754(第15题图)点B 在-1,0对应的两点(包括这两点)之间移动,则以下四个代数式的值,可能比2013大的是( D )A.b a -B. 1b a- C. 2()a b - D. 11a b - 10.观察下列正方形的四个顶点所标的数字规律,那么2013这个数标在( D )A. 第503个正方形的左下角B. 第503个正方形的右下角C. 第504个正方形的左下角D. 第504个正方形的右下角二、填空题(本题共有6小题,每小题5分,共30分. 请将答案填在题中横线上)11.定义:(,)(,)f a b b a =,(,)(,)g m n m n =--. 例如(2,3)(3,2)f =,(1,4)(1,4)g --=,则((5,6))g f -= (-6,5) .12.设32a =,b 是2a 的小数部分,则3(1)b +的值为 4 .13.设321025x y z x y z ++=⎧⎨++=⎩,则27x y z ++= 10 .14.如图,三角形ABC 的底边BC 长4厘米,BC 边上的高是2厘米,将三角形以每秒2厘米的速度沿高的方向向上移动3秒,这时,三角形扫过的面积是 28 平方厘米.15.如图,一个正方体的六个面上标着连续的整数,若相对面上所标数之和相等,则这六个数之和是 39 .16.如果α∠和β∠互补,且α∠>β∠,则下列表示β∠的余角的式子中:①90β-∠ ;C B A (第14题图)②90α∠- ;③1()2αβ∠+∠;④1()2αβ∠-∠. 其中正确的式子有 ①,②,④ (填写所有正确式子的序号).三、简答题(本题共有3小题,每小题10分,共30分. 务必写出详细解答过程)17.已知222450a b a b +--+=, 求1111(1)(2)(3)(4)(5)(2012)(2013)a b a b a b a b +++++++++++ 的值. 解:将222450a b a b +--+=变形,得22(1)(2)0a b -+-=.∵ 2(1)0a -≥,2(2)0b -≥, ∴ 10a -=,20b -=, 解得a =1,b =2.∴ 1111(1)(2)(3)(4)(5)(2012)(2013)a b a b a b a b +++++++++++ 111113355720132015=++++⨯⨯⨯⨯ 11111111123355720132015⎛⎫=-+-+-++- ⎪⎝⎭11120141007122015220152015⎛⎫=-=⨯= ⎪⎝⎭.18.星期天,妈妈带着小丁去买了2斤苹果和6斤橘子,共用去12元,妈妈说:“上星期天也是买了2斤苹果和6斤橘子,也是花了12元,可是今天的苹果价格下调了,橘子价格上涨了,并且上涨和下调的幅度..相同”. 试求上星期天苹果和橘子每斤的价格. 解:设上星期天苹果每斤x 元,橘子每斤y 元,价格调整的幅度为m . 根据题意,得26122(1)6(1)12x y x m y m +=⎧⎨-++=⎩ ①-②,得 2(3)0m x y -=∵ m ≠0, ∴ 30x y -=, 即 3x y =.把3x y =代入①,得23612y y ⨯+=, 解得 y =1.把y =1代入3x y =,得313x =⨯=.答:上星期天苹果每斤3元,橘子每斤1元.①②19.有依次排列的3个数:3,5,9,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,2,5,4,9,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,-1,2,3,5,-1,4,5,9,继续依次操作下去. 问:(1)从数串3,5,9开始操作,第100次操作以后所产生的那个新数串的所有数之和是多少?(2)如果从数串2,10,7开始操作,第n 次操作以后所产生的那个新数串的所有数之和是5n +19 (直接写出答案).解:(1)设给出的数串为a ,b ,c ,则第1操作后得到的新数串为:a ,b a -,b ,c b -,c ,其和为:()()()()()()a b a b c b c a b c b a c b a b c c a +-++-+=+++-+-=+++- 第二次操作后得到的新数串为:a ,2b a -,b a -,a ,b ,2c b -,c b -,b ,c , 其和为:(2)()(2)()a b a b a a b c b c b b c +-+-+++-+-++[]()(2)()(2)()a b c b a b a a c b c b b =+++-+-++-+-+()(22)a b c c a =+++-()2()a b c c a =+++-……………………依此规律,从数串a ,b ,c 开始,经第n 次操作以后所产生的那个新数串的所有数之和为()()a b c n c a +++-.∴ 从数串3,5,9开始操作,第100次操作以后所产生的那个新数串的所有数之和为: (3+5+9)+100×(9-3)=17+600=617.答:从数串3,5,9开始操作,第100次操作后所产生的那个新数串的所有数之和是617.。
数学竞赛试卷七年级【含答案】

数学竞赛试卷七年级【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 如果一个数的平方根是9,那么这个数是:A. 81B. 9C. 3D. -92. 下列哪个数是有理数?A. √2B. √3C. √5D. √93. 下列哪个数是整数?A. 3.14B. 2.5C. 5.0D. -3.54. 下列哪个数是负数?A. -1B. 0C. 1D. 25. 下列哪个数是偶数?A. 21B. 23C. 25D. 27二、判断题(每题1分,共5分)1. 两个负数相乘的结果是正数。
()2. 两个正数相乘的结果是负数。
()3. 两个负数相除的结果是正数。
()4. 两个正数相除的结果是负数。
()5. 0乘以任何数都等于0。
()三、填空题(每题1分,共5分)1. 如果一个数的平方是16,那么这个数是______。
2. 如果一个数的平方根是4,那么这个数是______。
3. 两个负数相乘的结果是______。
4. 两个正数相乘的结果是______。
5. 0乘以任何数都等于______。
四、简答题(每题2分,共10分)1. 请解释有理数的概念。
2. 请解释整数的概念。
3. 请解释负数的概念。
4. 请解释偶数的概念。
5. 请解释奇数的概念。
五、应用题(每题2分,共10分)1. 计算下列各式的值:a) -3 + 7b) 5 (-2)c) -4 × 6d) -9 ÷ 3e) 14 ÷ (-2)2. 判断下列各式的符号:a) -(-5)b) -(+8)c) -(-12)d) -(+15)e) -(-20)3. 计算下列各式的值:a) √16c) √36d) √49e) √644. 判断下列各数是否为整数,并解释原因:a) 3.14b) 2.5c) 5.0d) -3.5e) 8.95. 判断下列各数是否为负数,并解释原因:a) -1b) 0c) 1d) 2e) -3六、分析题(每题5分,共10分)1. 请分析并解释为什么两个负数相乘的结果是正数。
七年级数学“应用与创新”竞赛选拔比赛二

七年级数学“应用与创新”竞赛选拔比赛二 一﹨选择题[每题4分,共24分]1.已知02=--++y y x y x ,在数轴上给出关于x ﹨y 七年级数学“应用与创新”竞赛选拔比赛二有( )A .1种B .2种C .3种D .4种 2.如图,有一条公路修到湖边时,需拐弯而过,如果第一次拐弯处∠A =120,第二次拐弯处∠B =150,第三次拐弯后道路恰好与第一次拐弯前的道路平行,则第三次拐弯处的∠C =[ ]A .150B .130C .140D . 1203.一个四位数能被9整除,去掉末位数字后所得的三位数恰好是4的倍数 ,这样的四位数中最大的一个的末位数字是[ ]A ﹨ 6B ﹨ 4C ﹨ 2D ﹨34.一个商店以每3盘16元的价值购进一批录音带,又从另外一处以每4盘21元的价格购进比前一批数量加倍的录音带,如果两种录音带合在一起以每3盘K 元的价格全部出售,可得到所投资的20%的收益,则K 的值等于[ ]A.17B.18C.19D.205.如图,一个边长为3的等边三角形被分成9个边长为1的小等边三角形,把数字1,2,3,4,…,9填入这9个小等边三角形中,使得图中每个边长为2的等边三角形内的4个数字的和相等,则这个和的最大值和最小值分别是[ ]x y x y xy O xyA .24,16B .23,17C .22,17D .23,166.在某班的新年晚会上,每个同学都写若干字条祝福他人,已知在任意四个人中,每一位都祝福其他三个人中的至少一位,那么该班中没有得到其他同学祝福的字条的同学最多有[ ]位。
A.1B.2C.3D.4二﹨填空题[每题5分,共50分]7.已知实数,,a b c 满足()()()0a b b c c a +++=且0abc <,则代数式a b c a b c++的值是8.研究15, 12, 10这三个数的倒数发现121101151121-=-,我们称15, 12, 10这三个数为一组调和数,现有一组数调和数x, 5, 3 (x>5),则x 的值是9.甲﹨乙﹨丙﹨丁四种商品的单价分别为 2 元,3 元,5 元和 7 元,现从中选购了 6 件共花 费了 36 元。
2013年七年级数学竞赛试题及参考答案-------

2013年初中七年级数学竞赛试题一.选择题(每小题4分,共32分) 1.x 是任意有理数,则2|x |+x 的值( ).A .大于零B . 不大于零C .小于零D .不小于零2.在-0.1428中用数字3替换其中的一个非0数码后,使所得的数最大,则被替换的数字是( ) A .1 B .4 C .2 D .83.如图,在数轴上1的对应点A 、B , A 是线段BC 的中点,则点C 所表示的数是( )A.2 B2 C1 D.14.桌上放着4张扑克牌,全部正面朝下,其中恰有1张是老K 。
两人做游戏,游戏规则是:随机取2张牌并把它们翻开,若2张牌中没有老K ,则红方胜,否则蓝方胜。
则赢的机会大的一方是( )A .红方B .蓝方C .两方机会一样D .不知道 5.如果在正八边形硬纸板上剪下一个三角形(如图①中的阴影部分),那么图②,图③,图④中的阴影部分,均可由这个三角形通过一次平移、对称或旋转而得到.要得到图②,图③,图④中的阴影部分,依次进行的变换不可..行.的是( )A.平移、对称、旋转 B.平移、旋转、对称 C.平移、旋转、旋转 D.旋转、对称、旋转6.计算:22221111(1)(1)(1)(1)2342007---⋅⋅⋅-等于( ) A .10042007 B .10032007 C .20082007D .200620077.如图,三个天平的托盘中相同的物体质量相等。
图⑴、⑵所示的两个天平处于平衡状态要使第三个天平也保持平衡,则需在它的右盘中放置( )(3)(2)(1)A. 3个球B. 4个球C. 5个球D. 6个球8.用火柴棒搭三角形时,大家都知道,3根火柴棒只能搭成1种三角形,不妨记作它的边长分别为1,1,1;4根火柴棒不能搭成三角形;5根火柴棒只能搭成一种三角形,其边长分别为2,2,1;6根火柴棒只能搭成一种三角形,其边长分别为2,2,2;7根火柴棒只能搭成2种三角形,其边长分别为3,3,1和3,2,2;…;那么30根火柴棒能搭成三角形个数是( )A .15B .16C .18D .19 二.填空题(每题4分,共28分)9.定义a*b=ab+a+b,若3*x=31,则x 的值是_____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.13个小朋友围成一圈做游戏,规则是从某一个小朋友开始按顺时针方向数数,数到第13,该小朋友离开;这样继续下去.,直到最后剩下一个小朋友. 小明是1号,要使最后剩下的是小明自己,他应该建议从( )小朋友开始数起?
A、7号 B、8号 C、13号 D、2号
13.设 是大于1909的正整数,使得 为完全平方数的 的个数是()
A.3. B. 4. C. 5. D. 6.
14.100人共有2000元人民币,其中,任意10个人的钱数的和不超过380元。那么一个人最多能有()元
A.216B.218C.238D.236
三、解答题(共36分)
15.甲、乙两人先后去同一家商场买了一种每块0.50元的小手帕,商场规定凡购买了不少于10块小手帕的可优惠20%,结果甲比乙多花了4元钱,又知甲所花的钱不超过8元,在充分享受(如果能)优惠的条件下,甲、乙各买了多少块小手帕?(本题10分)
8.849.C10.B11.A 12.A
12.A(如果从1号数起,离圈的小朋友依次为13,1,3,6,10,5,2,4,9,11,12,7,最后留下8号,因此从逆时针方向退8名(即7号)开始数起,最后留下1号).13.B 分子与分母的和为100,在 中,
有 共4个
14.B将100中任意9人为一组,共11组余1人,每组9人和多余的那一人钱数的和不超过380元,(380×11-2000)÷10=218(元)
(A)25(B)66(C)91(D)120
10.已知 满足 ,则 的值为( )
(A)1. (B) . (C) . (D) .
11.一只船有一个漏洞,水以均匀速度进入船内。发现漏洞时船内已经进入了一些水,如果以12个人淘水,3小时可以淘完,如果以5个人淘水,10小时才能淘完。现在要想在2小时内淘完,需要( )人。
8.如图,在RtΔABC中,∠ACB=90°,∠ABC=62°,将ΔABC绕顶点C 旋转到ΔA´B´C的位置,使顶点B恰好落在斜边A´B´上,设A´C与AB相交于点D,则∠BDC的度数是
二、选择题(每小题4分,共24分)
9.如图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是()
15.9与1,15与4,20与10
16.解析设丈夫买了x件商品,妻子买了y件商品,则得不定方程x2-y2=63.
即(x+y)(x-y)=63=63×1=21×3=9×7.
可得方程组
解得
根据条件“孙先生所买的商品比赵女士多23件”,可确定x1为孙先生买的商品数,y2为赵女士买的商品件数;再根据条件“金先生所买的商品比李女士多11件”,可确定x2为金先生所买的商品件数,y3为李女士买的商品件数.
(本题10分)
17.(本题满分16分)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,写出作法并证明。(5分)
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。直接写出FE和FD之间的数量关系;(3分)
16.有三对夫妻一同上商店买东西.男的分别姓孙、姓陈、姓金,女的分别姓李、姓赵、姓尹。他们每人只买一种商品,并且每人所买商品的件数正好等于那种商品的单价(元数).现在知道每一个丈夫都比他的妻子多花63元,并且孙先生所买的商品比赵女士多23件,金先生所买的商品比李女士多11件,问孙先生、陈先生、金先生的爱人各是谁?
由此可判断出孙先生和尹女士为夫妻,金先生和赵女士是夫妻,陈先生和李女士是夫妻.
17.作轴对称的全等三角形(1分)写出画法(2分);证明过程(2分)
七年级数学应用与创新竞赛试题
(时间:共40分)
1.已知a=1999x+2000,b=1999x+2001,c=1999x+2002,则多项式a2+b2+c2-ab-bc-ca的值为
2.关于x,y的方程xy=x+y的整数解有_____组.
3.用 表示不大于 的最大整数,如果 ,那么 的取值范围是
4.正五边形广场ABCDE的周长为2000米.甲、乙两人分别从A、C两点同时出发,沿A→B→C→D→E→A→…方向绕广场行走,甲的速度为50米/分,乙的速度为46米/分.那么出发后经过分钟,甲、乙两人第一次行走在同一条边上.
5.一质点在一直线上从A点开始以每分钟2米的速度进行运动,其运动方式是:前进1米后退2米,前进3米后退4米,……,如此反复,当它第一次到达离A点10米的B点时要经过分钟。
6.10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实告诉两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报3的人心里想的数是;
7.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸, 结果比平时早20分钟到家,则小林步行________分钟遇到来接他的爸爸.
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中结论是否仍然成立?若成立,请证明;若不成立,请说明理由。(8分)
参考答案
1.32.23. 4.1045.956.-27.50
如图,小林学校在A,家在B,下午4点他步行从A出发,与按时从B来接他的车相遇于C,结果汽车由C返回B比往常提前了20分钟,表明汽车由C-A-C共需20分钟, 因此汽车由C到A需10分钟,则汽车在4:50与小林相遇,即小林步行50分钟遇到来接他的爸爸.
