四个热力学基本关系式和Maxwell公式的理解与记忆
物理化学maxwell关系式推导

物理化学maxwell关系式推导物理化学的maxwell关系式是一种非常重要的方程式,它描述了热力学系统中各种物理量之间的关系。
其中最为著名的就是关于熵(S)、温度(T)、压强(P)和体积(V)之间的四个关系式,可以用来计算和预测系统中的热力学性质。
下面我们将对这四个关系式进行详细的推导和解释。
首先,我们来看熵和温度之间的关系式,即:(1) (S/V)T = (P/T)V这个关系式描述了熵的体积导数与温度的关系,也就是说,在恒定温度下,系统中的熵随着体积的变化而变化,其变化率与温度有关。
这个关系式的推导涉及到热力学第一定律和热力学第二定律,具体推导过程可以参考相关教材和论文。
接下来是熵和压强之间的关系式,即:(2) (S/P)T = -(V/T)P这个关系式描述了熵的压强导数与温度的关系,也就是说,在恒定温度下,系统中的熵随着压强的变化而变化,其变化率与温度有关。
这个关系式的推导同样也涉及到热力学第一定律和热力学第二定律。
然后是体积和温度之间的关系式,即:(3) (V/T)P = (S/P)T / (S/V)T这个关系式描述了体积的温度导数与熵的压强和体积导数的比例关系,也就是说,在恒定压强下,系统中的体积随着温度的变化而变化,其变化率与熵的压强和体积导数的比例有关。
最后是体积和压强之间的关系式,即:(4) (V/P)T = -(S/P)T / (S/V)T这个关系式描述了体积的压强导数与熵的压强和体积导数的比例关系,也就是说,在恒定温度下,系统中的体积随着压强的变化而变化,其变化率与熵的压强和体积导数的比例有关。
以上就是maxwell关系式的四个基本方程式的推导过程和含义。
这些关系式为我们研究和理解热力学系统提供了有力的工具和方法,也为我们预测和设计新的热力学系统提供了重要的指导。
maxwell关系式推导

maxwell关系式推导Maxwell关系式是材料学和热力学中使用的一系列重要的关系式。
这些关系式用来描述物质的性质如何随着温度、压力和其他物理量的变化而变化。
在本文中,我们将讨论如何推导Maxwell方程式以及它们的应用。
Maxwell方程式的推导可以从熵的定义开始。
根据热力学的第二定律,熵被定义为系统内分子的无序性。
当一个物理系统处于平衡状态时,其熵最大。
因此,我们可以得到dS = dQ/T其中,dS代表系统熵的变化,dQ代表热量的变化,而T代表温度。
这个方程式成为热力学第一原理的推论,因为它说明了热量传递过程中的微观机制。
接下来,我们可以将熵的全微分表示为dS = (∂S/∂T)_p,dT + (∂S/∂p)_T,dp其中,p代表压力。
我们可以将这个式子中的温度T 和压力p进行变换,得出(∂T/∂p)_S = (∂V/∂S)_p(∂p/∂T)_V = (∂S/∂V)_T这些方程式被称为Maxwell关系式,其中第一个表达式被称为比热容关系式,第二个表达式被称为体积膨胀系数关系式。
这些方程式的应用非常广泛。
例如,在热力学中,我们通常需要估算物质的热容,可以使用比热容关系式。
对于液体和固体,我们通常采用Dulong-Petit定律,即比热容与摩尔质量无关。
而对于气体,则使用理想气体定律计算比热容。
体积膨胀系数关系式可以用来计算物质的可压缩性,这对于理解热力学的各种现象非常重要。
另一个应用Maxwell关系式的领域是相变热力学。
在这个过程中,物质的温度、压力和体积会发生改变,因此在理解相变过程中必须考虑这三个物理量的关系。
我们可以使用Maxwell方程式来推导物质在相变点附近的热力学性质,例如熔沸的温度和热容的跳跃等。
此外,Maxwell方程式还用于建立材料的热力学模型。
例如,在计算复杂材料的物性时,需要对材料进行建模,将其分解为若干个单元,然后使用熵和Maxwell方程式来描述单元之间的相互作用,从而推导出整个材料的物性。
热力学公式总结

热力学公式总结热力学是研究物质的能量转化和传递规律的科学。
在热力学的研究中,有一些重要的公式被广泛应用于不同领域,从工程到物理学。
下面将对一些常用的热力学公式进行总结,以便更好地理解和应用这些公式。
1. 热力学第一定律:能量守恒定律热力学第一定律是热力学的基本定律之一,它表明能量在系统中的转移和转化都是根据能量守恒定律进行的。
它可以表达为:系统的内能的增量等于系统所吸收的热量与所做的功的和。
这个公式的意义在于说明了能量是不会消失的,只会发生转化。
2. 热力学第二定律:熵增原理热力学第二定律是热力学的另一个重要定律,它描述了自然界中热量传递的方向性。
它可以表达为:孤立系统的熵不会减少,只会增加或保持不变。
这个公式的意义在于说明了自然界的趋势是向着熵增的方向发展,即系统的无序度会增加。
3. 热力学第三定律:绝对零度不可达性热力学第三定律是热力学中的一个重要定律,它表明在温度接近绝对零度时,系统的熵趋向于一个极小值,即趋向于零。
这个公式的意义在于说明了绝对零度是无法达到的,因为系统的熵无法减少到零。
4. 理想气体状态方程理想气体状态方程是描述理想气体行为的方程,它可以表达为PV=nRT,其中P表示气体的压强,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的温度。
这个公式的意义在于描述了理想气体的状态与其它参数之间的关系。
总结:热力学公式是描述能量转化和传递规律的工具,它们在热力学的研究和应用中发挥着重要作用。
通过理解和应用这些公式,我们可以更好地理解和解释自然界中的现象,同时也能够指导工程和科学研究的实践。
热力学公式的研究是热力学的基础,也是探索能量转化和传递规律的重要途径之一。
通过不断深入研究和应用,我们可以进一步推动热力学的发展,并为人类社会的进步做出更大的贡献。
热力学函数间的关系

计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
3.7 热力学基本方程及Maxwell关系式

恒T、p、W= 0: G 0
自发 平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明: 1. 等式右边只有四个物理量T,S, p,V
2. 十字交叉法:
对U来说,S,V分别表示dS和dV; dS对角线 对应T,dV对角线对应p;箭头方向表示正负,指向 为负,则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明:
1. 关系式中只有四个物理量T, S, p,V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量,而T和p为强 度量。同种性质的状态函数 的分式,不取负号。
分析:利用克拉佩龙方程 dT T βαVm
dp 解:由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分,得 lnT2
T1
3-7 热力学第二定律-麦克斯韦方程的应用

----d d d d d d d d d d d d V S p S V T p p U U U S V S V H H H S p S p A U A T VT V G G G T pT p ∂∂⎧⎛⎫⎛⎫=+ ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎪⎪⎛⎫∂∂⎛⎫=+ ⎪⎪ ⎪∂∂⎝⎭⎝⎭⎪⎨∂∂⎛⎫⎛⎫⎪=+ ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎪⎛⎫∂∂⎛⎫⎪=+ ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎩V Sp SV Tp TU U TpS V H H T VS p A A SpT V G G S V T p ∂∂⎧⎛⎫⎛⎫==- ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎪⎪⎛⎫∂∂⎛⎫== ⎪⎪ ⎪∂∂⎝⎭⎝⎭⎪⎨∂∂⎛⎫⎛⎫⎪=-=- ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎪⎛⎫∂∂⎛⎫⎪=-= ⎪ ⎪⎪∂∂⎝⎭⎝⎭⎩,,,,V p S T U d d d -=(1)p V S T H d d d +=(2)Vp T S A d d d --=(3)p V T S G d d d +-=(4)1、热力学四个基本公式Vp S T U d d d -=(1)pV S T H d d d +=(2)V p T S A d d d --=(3)p V T S G d d d +-=(4)()()V p U H S T S ∂∂==∂∂从公式(1),(2)导出()()S T p U A V V ∂∂=-=-∂∂从公式(1),(3)导出()()S T H G p V p ∂∂==∂∂从公式(2),(4)导出()()V pS A GT T ∂∂=-=-∂∂从公式(3),(4)导出2、Maxwell 关系式(1)求U 随V 的变化关系已知基本公式Vp S T U d d d -=等温对V 求偏微分()()T T UST pV V ∂∂=-∂∂()()T VSpV T ∂∂=∂∂V p T S A d d d --=3、Maxwell 关系式应用()()T VS pV T ∂∂=∂∂不易测定,根据Maxwell 关系式()T SV ∂∂所以()()T V UpT pV T ∂∂=-∂∂只要知道气体的状态方程,就可得到值,即等温时热力学能随体积的变化值。
热力学基本方程及Maxwell关系识记图

S
p (" ")
p
注意:只当偏微分中分子、分母同时出现V、T时才取“”号。
5
热力学基本方程及Maxwell关系 识记图
Mnemonic diagram (识记图一)
(-)
p
dU TdS pdV dH TdS Vdp dF SdT pdV dG SdT Vdp
dZ MdX NdY M N Y X X Y e.g
U
("" arrow pointedtoward)
S H p
Example:
V
T
T V S p p S S V p T p T
(" ") S
p T
S V
p (" ") T (" ")
注意:只有T 和V作变量时 才取“”号, p和S作变量时 肯定取“+”号。
(-)
S
T
Z Z ( X , Y ), Z U , H , F , G
U
H
F
G
Potentials(势)
S V p T p T
Mnemonic diagram(识记图三)
S
H p G
U
V F
① 太阳(Sun)照在树梢(Tree) 上,河流从山峰(peak)流向 河谷(Valley); ② U、G和H、F 两对朋友各坐 在1、3象限和2、4象限(方桌 前)打牌。
e.g U 有 S 、 V 两个帮手(特征变量) T dU=( ? )dS + ( ? )dV 箭头向外取“+”号; p T 箭头向内取“”号。 dU=( T )dS + ( p )dV
热力学基本关系式
衡态) (不可逆) 例3:单纯pVT变化(仅研究均匀系统←→平衡系统)
纯pg,混合气体 由T1,p1→→T2,p2可用基本方程
dU Tds pdV -----最基本 dG sdT VdP ----最常用
3.由热力学基本方程计算纯物质pVT 变化过程的ΔA ,ΔG
①恒温过程dT= 0 dAT pdV
a. pg: PV=nRT
dGT Vdp
AT
V2 pdV
V1
nRT ln V2 V1
GT
p2Vdp nRT ln p2
p1
p1
b.凝聚相(S,l):等温压缩率很小,→体积可认为不变
AT
p
T
H p
S
V
dA SdT pdV
A S T V
A p V T
dG SdT Vdp
G S T p
G p
T
V
T U H
S V S p
U A p
V S V T
V
H p
S
G p
T
A G S
T V T p
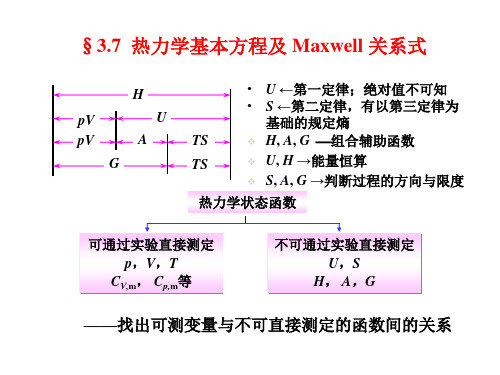
§3.7 热力学基本方程及 Maxwell 关系式
H
pV
U
pV
A
G
• U ←第一定律;绝对值不可知 • S ←第二定律,有以第三定律为
基础的规定熵
TS
❖ H, A, G 组合辅助函数
TS
❖ U, H →能量恒算
❖ S, A, G →判断过程的方向与限度
热力学状态函数
可通过实验直接测定 p,V,T
CV,m, Cp,m等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四个热力学基本关系式和Maxwell公式的理解与记忆摘要:准确理解并掌握热力学的四个基本关系式和Maxwell公式是学好热力学的一个重要前提。
在分析和讨论热力学四个基本关系式和Maxwell公式的导出的基础上,分析和讨论其使用条件,并结合这些关系式的特点,补充和完善了前人提出的热力学基本关系式的记忆方法;将Maxwell公式中的P、V、S和T四个变量共可给合出的24种偏导函数分为Maxwell公式原形偏导函数、等价函数和非Maxwell 公式偏导函数三类,分析了其结构特点,提出了一种新的逻辑清晰、简单易记的Maxwell公式的记忆方法。
关键词:热力学;关系式;Maxwell式;记忆方法
在学习化工热力学的过程中,学生经常感到一些关系式难以记忆。
虽然这些关系有些已经在物理化学中学过,但学生经常反映还是容易混淆。
准确理解这些关系式中所涉及各种函数的基本概念及其推导过程是学好化工热力学的根本,但学会一些巧妙的记忆方法还是会起到事半功倍的效果。
文献中也曾有过关于这些关系式的报道[1-4],但记忆起来仍然不是很方便。
这里仅就自己多年来讲授化工热力学课程所总结出来的一点记忆技巧和体会与大家分享。
一封闭体系的四个热力学基本关系
封闭体系的四个热力学基本关系是:
dU=TdS-pdV.[JY](1)
dH=TdS+Vdp.[JY](2)
dA=-SdT-pdV.[JY](3)
dG=-SdT+Vdp.[JY](4)
(一)推导与准确理解
这四个热力学基本关系式实质上是热力学第一定律和热力学第二定律在均相封闭中实用的一种数学表达。
对于封闭体系,体系与环境没有物质交换,只有能量交换。
不论是否为均相体系,体系内能的增加只是从环境得到的功和热之和,故由热力学第一定律总有dU=δQ+δW(此处规定了体系得到功或热为正,失去为负).[JY](5)
根据热力学第二定律,体系与环境交换的功和热必须满足
dS≥δQT即δQ≤TdS(仅对可逆过程取等号).[JY](6)
当系统与环境只有体积功交换时,
δW≤-pdV(仅对可逆过程取等号).[JY](7)
将式(6)和式(7)代入式(5),得到式
dU≤TdS-pdV.[JY](8)
再根据热焓H、Gibbs自由能G和Helmholtz自由能A的定义式H≡U+pV;
A≡U-TS;
G≡H-TS;
并分别取其全微分得到
dH=dU+pdV+Vdp;
dA=dU-TdS-SdT;
dG=H-TdS-SdT;
将式(8)代入上3式得出
dH≤TdS+Vdp.[JY](9)
dA≤-SdT-pdV.[JY](10)
dG≤-SdT+Vdp.[JY](11)
由推导过程中的假设知,式(8)式(11)的适应条件为只有体积功的封闭体系。
式中所有的物理量均为状态函数,当体系达到完全平衡状态时,其值已确定,此时状态函数的变化值与过程无关。
故不论变化过程是
否可逆,式(8)式(11)均取等号,得到式(1)式(4)。
所谓完全平衡即达到热平衡、力平衡、化学势平衡。
换句话说,即体系中各处不仅达到了温度和压力不再随时间发生变化,而且体系的组成也不再随时间发生变化。
在教科书中通常会看到式(1)式(4)的适用条件为:只有体积功且无化学反应的均相封闭体系。
那么这里为什么要加上一个无化学反应的限制条件呢?其实有没有这个化学反应条件的限制取决于我们如何来理解均相封闭体系的平衡状态。
如果我们把均相封闭体系理解为达到了完全的平衡状态,则无需要求无化学反应这个限定条件;如果把均相封闭体系理解为只是达到了热平衡、力平衡和宏观上的化学组成平衡状态,则还会因化学反应的存在,导致体系组成发生改变,即相当于反应物从系统中移出,而生成物从环境移入到体系。
这样,体系就等价于是一个开放体系了。
同样,对于非均相的封闭体系,只要已经达到了相平衡状态,式(1)式(4)是同样成立的。
有时我们之所以特意强调其适用条件为均相封闭体系是为避免一些特殊情况。
例如,定组分汽液两相封闭体系。
当未达到汽液平衡时,宏观上看其温度、压力和组成并不再随时间发生变化,但体系可能会因吸热或放热发生气液两相量和组成的调整,从而引起导致状态函数发生变化。
(二)记忆方法
夏亿谦[5]、何展荣[6]、林金朝[7]曾分别提出热力学基本关系式的多种不同的四边形记忆法;王树国[8]和宋小利[4]提出
过坐标象限法,李德光[2]提出了双四边形法等。
其中,笔者认为陈金友提出的记忆方法比较直观易记[9]。
热力学四个基本关系式共涉及8个物理量,其中U,H,A和G为四个能量量纲函数;P,V,S和T为非能量量纲函数。
如果把这8个物理量摆成图1所示的图形,则构成4条连接线。
