热力学函数基本关系式
合集下载
热力学第一定律总结

298 K时,H2(g)的∆cHmө = -285.83 kJ·mol-1, H2S(g)和 SO2(g)的∆fHmө分别为-20.63 kJ·mol-1和-296.83 kJ·mol-1。 求下列反应在498 K时的∆rUmө。已知水在373 K时的摩 尔蒸发焓∆vapHm (H2O, 373 K) = 40.668 kJ·mol-1. 2H2S (g) + 3O2 (g) = 2SO2 (g) + 2H2O(g)
其中,T2的值由理想气体绝热方程式(pVγ=C)求得。
3、Q的计算 、 的计算
• Q = ∆U – W • 如恒容,Q = ∆U • 如恒压,Q = ∆H
1. 绝热密闭体系里,以下过程的ΔU不等于零的是: A) 非理想气体混合 B) 白磷自燃 C) 乙醚挥发 D) 以上均为0 2.“爆竹声中一岁除,春风送暖入屠苏”。我国 春节有放鞭炮的习俗。在爆竹爆炸的过程中,以 下热力学量的符号表示正确的是(忽略点火时火柴 传递给引线的少量热量) ( ) A) Q<0,W<0,ΔU<0 B) Q<0,W=0,ΔU<0 C) Q=0,W<0,ΔU<0 D) Q=0,W=0,ΔU=0
nN2CV, m(N2)(T-T1) + nCuCV,误二: ∆U =∆UN2 + ∆UCu = 0
nN2CV, m(N2)*(T-T1) + nCuCV, m(Cu)*(T-T2) = 0
正确解法:
∆U =∆UN2 + ∆UCu = ∆UN2 + ∆HCu = 0 nN2CV, m(N2)*(T-T1) + nCuCp, m(Cu)*(T-T2) = 0
• 求火焰最高温度: Qp = 0, ΔH = 0 求火焰最高温度: • 求爆炸最高温度、最高压力:QV = 0, W = 0 求爆炸最高温度、最高压力: =0
热力学函数的基本关系式

dU = TdS- pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = -SdT- pdV
(1-110)
dG = -SdT + Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
常用的是式(1-120)及式(1-121),这两等式右边的变化率是可以由 实验直接测定的,而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU=TdS-pdV
定温下, dUT=TdST-pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为:
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
(эG/эP)T,n=V
(э△G/эP)T,n=△V 此即G---V关系式
只要知道△V--p关系式,在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得: (△G)2/ T2- (△G)1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而: △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
热力学函数的基本关系式

dG = -SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 :表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法:
T p
S
V S
p
① 对角乘积永远是pV,TS;
② 等式两边分母与外角标互换;
S p
T
V T
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习:由热力学基本方程出发证明,
H p
T
T
V T
p
V
证明:
dH=TdS+Vdp
定温下,等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程
物理化学(机材类第四版,ppt课件)2.9 热力学基本关系式

适用条件:组成不变,W′= 0 的封闭系统或 封闭系统,W′= 0,可逆过程。
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
(c) A=U-TS 微分,并用上式代入得到
dA = -SdT- pdV
(d) G = H – T S微分,并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
(一定量、一定组成的单相系统)
➢理想气体 U、H 只是T 的函数,与p、V 无关;S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 ()
A T
V
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
(c) A=U-TS 微分,并用上式代入得到
dA = -SdT- pdV
(d) G = H – T S微分,并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
(一定量、一定组成的单相系统)
➢理想气体 U、H 只是T 的函数,与p、V 无关;S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 ()
A T
V
热力学函数间的关系

则T = 1000 K, rG1000 = 61900 Jmol-1>0
计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
6.热力学基本关系式
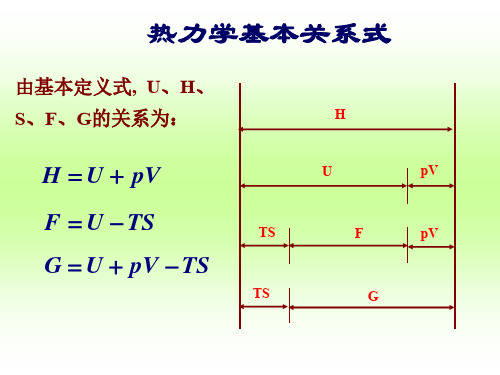
G U pV TS
dG S dT V d p
U、H、F、G这些热力学函数之间的关系实质是勒让德变换 勒让德变换实际上是在我们得到了一个不变量后,要得到它的对偶自变量下的 不变量的一个重要的变换。
热力学四个基本关系式(Gibbs关系式)如下:
d U T d S p dV
S p V T T V
(1)
U p V T T p T V
得证
几个重要的偏导关系式
1.与S有关的
S p V T T V
S V T p p T
d H T d S V d p
(1)
(2) (3)
d F S d T p dV dG S dT V d p
(4)
条件: 简单封闭系统,只作体积功。
• 基本关系式实质上是 U 、 H 、 F 和 G 的数学全 微分展开式。 • 简单的封闭系统, 状态只需两个独立变量即可 决定, 这两个变量可以任意选取. • 从四个关系式的微分变量可知, 对不同的状态 函数, 在作全微分展开时, 选取的独立变量是 不一样的:
例: 试证明:
U p V T T p T V
解:有基本热力学关系式
d U T d S p dV
在等温条件下,求内能对体积的偏微商:
U S V T V p T T
由麦克斯韦关系式: 代入(1)式得:
Wf 0
Qr T d S
将上式代入内能的全微分:
W p dV
d U T d S p dV
(1)
3.7 热力学基本方程及Maxwell关系式

恒T、p、W= 0: G 0
自发 平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明: 1. 等式右边只有四个物理量T,S, p,V
2. 十字交叉法:
对U来说,S,V分别表示dS和dV; dS对角线 对应T,dV对角线对应p;箭头方向表示正负,指向 为负,则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明:
1. 关系式中只有四个物理量T, S, p,V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量,而T和p为强 度量。同种性质的状态函数 的分式,不取负号。
分析:利用克拉佩龙方程 dT T βαVm
dp 解:由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分,得 lnT2
T1
热力学函数间的关系

T2 G2 G1 H = ∫ 2 dT T1 T2 T1 T rGm 2 rGm1 1 1 = rHm( ) T2 T1 T2 T1
r Gm ,2
1.400 × 105 1 1 5 ) = 1.966 × 10 ( 873 298 873 298
r Gm ,2 = 30820J mol -1
吉布斯- 吉布斯-亥姆赫兹方程式
G T = H T2 T P
(微分形式)
应用:在等压下若已知反应在 应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T 时的 应在 2时的rGm(T2)。 积分形式
∫
T2
T1
T2 G H ( ) = ∫ 2 dT T1 T T
( V V ) p dT = ( )T dp T p
1mol理想气体, PV = RT 理想气体, 理想气体 p T ( )p = , R V V V ( )T = , p p R p ( )V = V T 则 ( T ) p ( V )T ( p )V = 1
V p T
可写成
T V p ( )p( )T ( )V = 1 V p T
2010-8-2
三、Maxwell 关系式
证明: 例3证明:(
T V p )p( )T ( )V = 1 并以理想气体验证上式的正确。 并以理想气体验证上式的正确。 V p T
定量纯气体, 证: 定量纯气体, V = f (p,T)
dV = ( V V ) p dT + ( )T dp T p
当V恒定,dV = 0,则 恒定, , 恒定
dU = Td S pdV
U S 等温对V求偏微分 等温对 求偏微分 ( )T = T ( )T p V V
S p S 不易测定,根据Maxwell关系式 ( )T = ( ) V 关系式 ( )T 不易测定,根据 V T V
r Gm ,2
1.400 × 105 1 1 5 ) = 1.966 × 10 ( 873 298 873 298
r Gm ,2 = 30820J mol -1
吉布斯- 吉布斯-亥姆赫兹方程式
G T = H T2 T P
(微分形式)
应用:在等压下若已知反应在 应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T 时的 应在 2时的rGm(T2)。 积分形式
∫
T2
T1
T2 G H ( ) = ∫ 2 dT T1 T T
( V V ) p dT = ( )T dp T p
1mol理想气体, PV = RT 理想气体, 理想气体 p T ( )p = , R V V V ( )T = , p p R p ( )V = V T 则 ( T ) p ( V )T ( p )V = 1
V p T
可写成
T V p ( )p( )T ( )V = 1 V p T
2010-8-2
三、Maxwell 关系式
证明: 例3证明:(
T V p )p( )T ( )V = 1 并以理想气体验证上式的正确。 并以理想气体验证上式的正确。 V p T
定量纯气体, 证: 定量纯气体, V = f (p,T)
dV = ( V V ) p dT + ( )T dp T p
当V恒定,dV = 0,则 恒定, , 恒定
dU = Td S pdV
U S 等温对V求偏微分 等温对 求偏微分 ( )T = T ( )T p V V
S p S 不易测定,根据Maxwell关系式 ( )T = ( ) V 关系式 ( )T 不易测定,根据 V T V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V S ( ) p d p T
S V d p
p
从状态方程求得 ,V 与 p 的关系,就可求 ( S )T 或 S 。
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
物化课件
例如,对理想气体
pV nRT,
( S p )T
常用的特征变量为:
G(T , p)
U (S,V )
上一内容
下一内容
A(T ,V ) H (S, p)
回主目录
S(H, p)
返回
2018/11/23
特性函数
物化课件
例如,从特性函数G及其特征变量T,p,求H,U, A,S等函数的表达式。 G(T , p) dG SdT Vdp G 导出: V ( G ) T S ( ) p p T
V =C p dT [V T ( ) p ]dp T
V H C p dT [V T ( ) p ]dp T
知道气体状态方程,求出( V ) p 值,就可计算 H值。
T
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
等温对p求偏微分 ( H )T T ( S )T V
( S )T 不易测定,据Maxwell关系式 p
(
所以
H V ( )T V T ( ) p p T
只要知道气体的状态方程,就可求得 ( H )T p 值,即等温时焓随压力的变化值。
上一内容
下一内容 回主目录 返回
dA SdT pdV
(
(4) dG SdT Vdp
利用该关系式可将实验可测偏微商来代替那些不易直 接测定的偏微商。
上一内容
下一内容 回主目录 返回
2018/11/23
S p ( )T ( )V V T S V ( )T ( ) p p T
T V )S ( ) p p S
2018/11/23
Maxwell 关系式的应用
利用 (
物化课件
例2 态变化时的 U 值。设某气体从P1,V1,T1至P2,V2,T2, 求U ? U U (T ,V ) 解: U U dU ( )V dT ( ) T dV T V p =CV dT [T ( )V p ]dV T p U CV dT [T ( )V p ]dV T
物化课件
(3)Gibbs 自由能定义式。在等温、等压、可逆条件 下,它的降低值等于体系所作最大非膨胀功。
G H TS
或
G A pV
G Wf ,max (dT 0,dp 0, 可逆)
上一内容
下一内容
回主目录
返回
2018/11/23
函数间关系的图示式
物化课件
上一内容
下一内容
回主目录
返回
2018/11/23
四个基本公式
(1)
dU TdS pdV
物化课件
因为
dU Q pdV Q dS 代入上式即得。 T
这是热力学第一与第二定律的联合公式,适用 于组成恒定、不作非膨胀功的封闭体系。 虽然用到了Q TdS 的公式,但适用于任何可逆或 不可逆过程,因为式中的物理量皆是状态函数,其变 化值仅决定于始、终态。但只有在可逆过程中 TdS 才代 pdV 才代表 We 。 表 QR , 公式(1)是四个基本公式中最基本的一个。
物化课件
S p ( )T ( ) V V T
所以
U p ( )T T ( ) V p V T
只要知道气体的状态方程,就可得到 ( U )T 值,即 V 等温时热力学能随体积的变化值。
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
H U pV
H Q p
(dp 0,Wf 0)
(2)Helmholz 自由能定义式。在等温、可逆条件下, 它的降低值等于体系所作的最大功。
A U TS
A Wmax
上一内容
下一内容 回主目录
(dT 0, 可逆)
返回
2018/11/23
几个函数的定义式
Maxwell 关系式的应用
(1)求U随V的变化关系 已知基本公式 dU TdS pdV 等温对V求偏微分
物化课件
U S ( )T T ( )T p V V
上一内容
下一内容
回主目录
返回
2018/11/23
Maxwell 关系式的应用
S ( )T 不易测定,根据Maxwell关系式 V
例1
物化课件
证明理想气体的热力学能只是温度的函数。
解:对理想气体, pV nRT
p nRT /V
p nR ( )V T V
p U ( )T T ( )V p V T T nR p 0 V
所以,理想气体的热力学能只是温度的函数。
上一内容
下一内容 回主目录 返回
2.7 热力学函数基本关系式
• • • • • 几个函数的定义式 函数间关系的图示式 四个基本公式 从基本公式导出的关系式 特性函数
物化课件
• Maxwell 关系式 •
上一内容
Gibbs-Helmholtz方程
下一内容 回主目录 返回
2018/11/23
几个函数的定义式
物化课件
定义式适用于任何热力学平衡态体系,只是在特 定的条件下才有明确的物理意义。 (1)焓的定义式。在等压、 H Qp。 Wf 0 的条件下,
下一内容 回主目录 返回
2018/11/23
T
Maxwell 关系式的应用
(3)求 S 随 P 或V 的变化关系
物化课件
S V 根据Maxwell关系式: ( )T ( ) p V p T
等压热膨胀系数(isobaric thermal expansirity)定义: V 1 V ( ) p V 则 ( )p T V T
上一内容
下一内容 回主目录 返回
2018/11/23
四个基本公式
物化课件
(2) 因为
dH TdS Vdp
H U pV
dH dU pdV Vdp
dU TdS pdV
所以
dH TdS Vdp
上一内容
下一内容
回主目录
返回
2018/11/23
四个基本公式
T
U )T 的关系式,可以求出气体在状 V
知道气体的状态方程,求出 ( p )V 的值,就可计算U 值。
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
(2)求H 随 p 的变化关系
物化课件
已知基本公式
dH TdS Vdp
p p
S V )T ( ) p p T
H G TS
U H pV
G G G T ( ) p p( )T T p
G G T( )p T
A G pV
上一内容
下一内容 回主目录
G G p ( )T p
返回
2018/11/23
Maxwell 关系式
全微分的性质
物化课件
设函数 z 的独立变量为x,y, z具有全微分性质
物化课件
<3>
根据应用(1) (
U p )T T ( )V p V T
代入<3>式得
<4>
p V C p CV T ( )V ( ) p T T
只要知道气体的状态方程,代入可得 Cp CV 的 值。若是理想气体,则 Cp CV nR
从公式(3),(4)导出
上一内容
下一内容 回主目录
U H T ( )V ( )p S S U A p ( ) S ( )T V V H G V ( ) S ( )T p p
(3) (4)
dA SdT pdV dG SdT Vdp
dH TdS Vdp
所以
dG SdT Vdp
上一内容
下一内容
回主目录
返回
2018/11/23
物化课件 从基本公式导出的关系式对应系数关系式
(1) (2)
dU TdS pdV dH TdS Vdp
从公式(1),(2)导出 从公式(1),(3)导出
从公式(2),(4)导出
z z ( x, y )
z z dz ( ) y dx ( ) x dy Mdx Ndy x y M 和N也是 x,y 的函数 M 2 z N 2 z ( )x , ( )y y xy x xy M N 所以 ( )x ( ) y y xLeabharlann p2 p1(V T
) p V
nR p
nR p
S
上一内容
nR p
dp nR ln
p1 p2
nR ln
V2 V1
下一内容
回主目录
返回
2018/11/23
Maxwell 关系式的应用
(4)Cp与CV的关系
物化课件
根据热力学第一定律
C p CV (
H U (U pV ) U )p ( )V =[ ]p ( )V T T T T U V U =( ) p p( )p ( )V T T T U U 设 U U (T ,V ) , 则 dU ( )V dT ( )T dV T V
2018/11/23
