第九章_拉普拉氏变换(二)
合集下载
9.3 拉普拉斯逆变换

§9.3 Laplace 逆变换 第 九 章 拉 普 拉 斯 变 换
轻松一下 ……
18
§9.3 Laplace 逆变换
利用留数计算反演积分的定理证明 第 附: 九 章 证明 如图,作闭曲线 C L C R , 当 R 充分 CR st 大时,可使 的所有奇点包含 F ( s ) e 拉
普 拉 斯 变 换 在 C 围成的区域内。由留数定理有:
e2 t et t et .
12
§9.3 Laplace 逆变换 第 九 章 解 方法一 利用查表法求解 拉 普 拉 斯 变 换
( s 1)2 (1) F ( s ) [( s 1)2 4] ( s 3)
B s C (s 1) 2 C B 1 1 A 2 , 2 , 2 2 s3 (s ) 1 ( s1 )4 2
§9.3 Laplace 逆变换 第 九 章 拉 普 拉 斯 变 换
§9.3 Laplace 逆变换
一、反演积分公式 —— Laplace 逆变换公式 二、求 Laplace 逆变换的方法
1
§9.3 Laplace 逆变换 第 一、反演积分公式 —— Laplace 逆变换公式 九 章 1. 公式推导 推导 (1) 由 Laplace 变换与 Fourier 变换的关系可知, 拉 普 函数 f (t ) 的 Laplace 变换 F ( s ) F ( j ) 拉 斯 就是函数 f ( t ) u( t ) e t 的 Fourier 变换, 变 t j t 换 F ( s ) F ( j ) [ f ( t ) u ( t ) e ] e dt . 即 (2) 根据 Fourier 逆变换,在 f (t ) 的连续点 t 处,有
第九章 拉氏变换.

s sa
例3 求正弦函数f(t)=sinkt(k为实数)的laplace变换
解: L[ f (t )] sinktestdt 0
1 (e jkt e jkt )e st dt 0 2j
1 2j
[ s
1 jk
s
1] jk
s2
k
k2
例4 求余弦函数f(t)=coskt(k为实数)的laplace变换
I
0
f (t)
est d s
s
d
t
0
f
(t )
1 est t
s
dt
f (t) es t
dt
L[
f (t) ]
0t
t
推论:
L
1 tn
f
t
s
dss
ds
s
F
sds
n次
例11 求函数 f(t) = sint / t 的拉氏变换
解:
由于 L(sint)
1 s2 1
则由象函数积分性质有
第九章 拉普拉斯变换
§9.1 拉普拉斯变换的概念
§9.2 拉氏变换的性质 §9.3 拉氏逆变换 §9.4 拉氏变换的应用
引言
Fourier变换的限制:
绝对可积
指数衰减函数et (>0)
在整个数轴上有定义
单位阶跃函数u(t)
演变为拉氏变换
L[ f (t)] F[ f (t) e t u(t)] f (t) e( jw)tdt 0
sint 1
L[ f (t)] L[
t
] s
s2
ds 1
=
arccots
即 sint estdt arc cot s 令s = 0得
例3 求正弦函数f(t)=sinkt(k为实数)的laplace变换
解: L[ f (t )] sinktestdt 0
1 (e jkt e jkt )e st dt 0 2j
1 2j
[ s
1 jk
s
1] jk
s2
k
k2
例4 求余弦函数f(t)=coskt(k为实数)的laplace变换
I
0
f (t)
est d s
s
d
t
0
f
(t )
1 est t
s
dt
f (t) es t
dt
L[
f (t) ]
0t
t
推论:
L
1 tn
f
t
s
dss
ds
s
F
sds
n次
例11 求函数 f(t) = sint / t 的拉氏变换
解:
由于 L(sint)
1 s2 1
则由象函数积分性质有
第九章 拉普拉斯变换
§9.1 拉普拉斯变换的概念
§9.2 拉氏变换的性质 §9.3 拉氏逆变换 §9.4 拉氏变换的应用
引言
Fourier变换的限制:
绝对可积
指数衰减函数et (>0)
在整个数轴上有定义
单位阶跃函数u(t)
演变为拉氏变换
L[ f (t)] F[ f (t) e t u(t)] f (t) e( jw)tdt 0
sint 1
L[ f (t)] L[
t
] s
s2
ds 1
=
arccots
即 sint estdt arc cot s 令s = 0得
电路原理-拉普拉斯变换PPT课件
收敛域为s平面的右半平面
[ (t)] 1
s
7
例2 求单位冲激函数 (t)的拉普拉斯象函数。
解:
[ (t)] (t)estdt 0
0
(t
)e
st
dt
(t)estdt
0
0
est t0 1
收敛域包括整个s平面。
[ (t)] 1
[sint (t)] s2 2
10
2. 微分定理 (differentiation theorem)
d dt
f (t)
s
f (t) f (0 )
*证明:
d
dt
f (t)
e st d f (t )dt
0
dt
e stdf (t )
f (t)
0
f ()
f (0 )
lim sF(s)
s0
f
(0 )
lim f (t) limsF(s)
t
s0
利用初值定理和终值定理,根据已知的象函数
F(s)可直接在复频域中确定其对应原函数f(t)的初值
和终值。
21
例8 设 f (t) (1 et ) (t) 验证初值定理和终值定理。
2!
t (t)
1 s3
t (n
n1
1)!
(
t
)
1 sn
1
1 sn
t n1 (n 1)!
(t )
16
4. 时域位移定理 (time-shift theorem)
拉普拉氏变换

1
f1 ( t ) A 2 f 2 ( t ) A1 f1 ( t ) A2 f 2 ( t )
[ f 2 ( t )] F2 ( S )
A1 F1 ( S ) A 2 F2 ( S )
0 A1 f1 ( t ) A 2 f 2 ( t )e st dt 证: A1 f1 ( t ) A 2 f 2 ( t )
s0
例2:
R
(t)
校验:
+
u
uc (0 ) 0 du RC u (t ) dt
1 SRCU ( S ) U ( S ) S 1 U(S) S (1 SRC )
- C
1 1 u(0 ) lim S lim 0 s S (1 SRC ) s (1 SRC ) 1 u( ) lim 1 s 0 (1 SRC )
简写 F (s)
s为复频率
f ( t )
s j
应用拉氏变换进行电路分析称为电路的复频域分析 法,又称运算法。
2. 拉氏变换的定义
t < 0 , f(t)=0
正变换
F (s) f (t )e st dt 0 1 c j st f (t ) c j F (s)e ds 2j
设:
注
[ f ( t )] F ( s )
则:
[ f ( t t0 )] e st F ( s )
0
f ( t t0 ) 0 当 t t0
证:
令t t0
f(t - t )
0
t f ( t t0 )e
0
0
f ( t t0 )e st dt
f1 ( t ) A 2 f 2 ( t ) A1 f1 ( t ) A2 f 2 ( t )
[ f 2 ( t )] F2 ( S )
A1 F1 ( S ) A 2 F2 ( S )
0 A1 f1 ( t ) A 2 f 2 ( t )e st dt 证: A1 f1 ( t ) A 2 f 2 ( t )
s0
例2:
R
(t)
校验:
+
u
uc (0 ) 0 du RC u (t ) dt
1 SRCU ( S ) U ( S ) S 1 U(S) S (1 SRC )
- C
1 1 u(0 ) lim S lim 0 s S (1 SRC ) s (1 SRC ) 1 u( ) lim 1 s 0 (1 SRC )
简写 F (s)
s为复频率
f ( t )
s j
应用拉氏变换进行电路分析称为电路的复频域分析 法,又称运算法。
2. 拉氏变换的定义
t < 0 , f(t)=0
正变换
F (s) f (t )e st dt 0 1 c j st f (t ) c j F (s)e ds 2j
设:
注
[ f ( t )] F ( s )
则:
[ f ( t t0 )] e st F ( s )
0
f ( t t0 ) 0 当 t t0
证:
令t t0
f(t - t )
0
t f ( t t0 )e
0
0
f ( t t0 )e st dt
拉氏变换

3、积分定理
f(t)先积分再取拉氏变换,由积分定理有:
F ( s ) f ( 1 ) ( 0 ) L [ f ( t )dt ] s s
1 f 式中, 0 f t dt在0时刻的初始值。
( 1 ) ( 2 ) F ( s ) f ( 0 ) f (0 ) 2 L [ f ( t )( dt ) ] 2 2 s s s
X ( s)
0 例1、求指数函数 f ( t ) at e
(t 0 ) (t 0 )
的拉氏变换 F( s ) 。
变量置换法
解:由拉氏变换的定义式有:
F ( s ) f ( t )e
0
st
dt e e
0
at st
dt e
0
( a s )t
L [ ( t )] 1
常用函数的Laplace变换见附表-1。
三、拉氏变换的基本定理
1、性线定理
(1)比例性
L[ af ( t )] aF( s )
(2)叠加性
L[ f1 ( t ) f 2 ( t )] F1 ( s ) F2 ( s )
2、微分定理
原函数的导数的拉氏变换为: 一阶导:
例(1)f(t)的拉氏变换为 F ( s ) ,应用终值定理求f(t)的 s( s 5 ) 终值。 1 (2)已知F ( s ) ( s 1 ) ,应用初值定理求 f ( 0 )和f ( 0 ) 的值。
2
5
解:(1)由终值定理有:
lim f (t ) lim s F ( s) lim s
于是:
st st st 0 ( te )dt 0 e dt 0 ste dt
拉普拉斯变换的性质
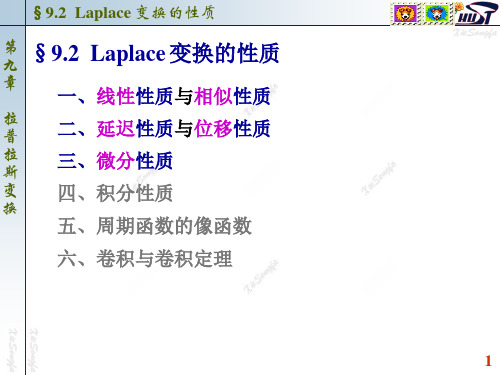
f (t ) 拉 s F ( s) d s [ t ]. 普 拉 斯 一般地,有 变 ds ds s F ( s) d s 换 s s
[
f (t ) ]. n t
n次
20
§9.2 Laplace 变换的性质 第 九 章 拉 普 拉 斯 变 换
9
§9.2 Laplace 变换的性质 第 二、延迟性质与位移性质 九 章 2. 位移性质
[e f ( t )] F ( s a ) . ( a 为复常数 ) 拉 普 拉 s 1 t 斯 [ e cos t ] . 例如 2 变 ( s 1) 1 换 1 [ e t sin t ] . 2 ( s 1) 1
2( s 6 24s 2 32) . 3 2 3 s ( s 4)
16
§9.2 Laplace 变换的性质 第 九 章 解 已知 拉 普 拉 斯 变 换2 [ sin 2 t ] 2 , 2 s 2 3t
根据位移性质有
[e
2 sin 2t ] , 2 ( s 3) 4
令 x t
0
f ( x ) e s x e s d x
e s F ( s ) .
6
§9.2 Laplace 变换的性质 第 二、延迟性质与位移性质 九 章 1. 延迟性质
( 为非负实数 )
[ f (t )] e s F ( s ) . f (t ) 0 , 则: 拉 性质 设 当 t < 0 时 普 拉 f ( t ) 0 这一约定。 斯 注意 性质中强调了当 t < 0 时 变 因此,本性质也可直接表述为: 换 [ f (t ) u(t ) ] e s F ( s ) .
[
f (t ) ]. n t
n次
20
§9.2 Laplace 变换的性质 第 九 章 拉 普 拉 斯 变 换
9
§9.2 Laplace 变换的性质 第 二、延迟性质与位移性质 九 章 2. 位移性质
[e f ( t )] F ( s a ) . ( a 为复常数 ) 拉 普 拉 s 1 t 斯 [ e cos t ] . 例如 2 变 ( s 1) 1 换 1 [ e t sin t ] . 2 ( s 1) 1
2( s 6 24s 2 32) . 3 2 3 s ( s 4)
16
§9.2 Laplace 变换的性质 第 九 章 解 已知 拉 普 拉 斯 变 换2 [ sin 2 t ] 2 , 2 s 2 3t
根据位移性质有
[e
2 sin 2t ] , 2 ( s 3) 4
令 x t
0
f ( x ) e s x e s d x
e s F ( s ) .
6
§9.2 Laplace 变换的性质 第 二、延迟性质与位移性质 九 章 1. 延迟性质
( 为非负实数 )
[ f (t )] e s F ( s ) . f (t ) 0 , 则: 拉 性质 设 当 t < 0 时 普 拉 f ( t ) 0 这一约定。 斯 注意 性质中强调了当 t < 0 时 变 因此,本性质也可直接表述为: 换 [ f (t ) u(t ) ] e s F ( s ) .
拉氏变换

0
(t
)e
st
dt
=e-s(0)
=1
0
(2)指数函数 f(t) =eat
a为实数
F(s) L[ f (t)] eatestdt 0
1
e(sa)t
sa
0
1 sa
§13. 2 拉普拉斯变换的基本性质
一、线性性质
设f1(t)和f2(t)是两个任意的时间函数,它们的 象函数分别为F1(s) 和F2(s) ,A1和A2是两个任意实 常数,
1 (s a)2
常用函数的拉氏变换表见教材P294。
第三节:传递函数
常用函数拉普拉斯变换对照表
原函数f (t) 象函数F (S)
(t)
1
1
1(t )
s
t
1 t2
1 s2
1
2
s3
e at
1 sa
一、单位阶跃函数 (Unit step function)
(t)
1. 定义
(t)
0 1
(t 0- ) (t 0 )
二、拉普拉斯变换及反变换
1、拉普拉斯变换(拉氏变换) 一个定义在[0,∞)区间的函数f(t),它的拉普
拉斯变换式F(s)定义为
F(s) f (t)estdt 0
式中 s =δ+jω为复数,F(s)称为f(t)的象函数,f(t) 称为F(s)的原函数。
est 称为收敛因子。
积分的结果不再是 t 的函数,而是复变量 s的函数。 所以拉氏变换是把一个时间域的函数f(t)变换到 s 域内的 复变函数F(s)。
O
t
2. 延迟单位阶跃函数
0
(t
t 0
)
1
(t t ) 0-
拉普拉氏变换与反变换

理:
L[e x(t )] X (s a)
5、延时定理:
at
L[ x(t a) 1(t a)] eas X (s)
6、初值定理:
t 0
lim x(t ) lim sX ( s )
s
7、终值定理:
lim x(t ) lim sX ( s )
分解因式,根据不同情况,利用待定系数法求反拉 氏变换
拉氏变换的运用
求解微分方程
X (s) L[ x(t )] x(t )est dt ˆ
0
式中:s为复变量;x(t)为原函数;X(s)为象函数
二、简单拉氏变换: 1、单位阶跃函数1(t) 2、指数函数 e at 3、正弦函数sinωt和余弦函数cosωt 利用欧拉公式 e j cos j sin
e j cos j sin e j e j sin 2j e j e j cos 2j
4、幂函数tn 利用Γ(gama)函数的性质:
(a ) x a 1e x dx ˆ
0
(n 1) n(n) n! u st u t s 1 dt du s L[t ] t e dt
拉普拉氏变换与反变换
一、定义: 对于函数 x(t ),如果满足下列条件: x (1)当t<0时, (t ) =0; 当t>0时,x(t)在每个有限区间上是分段连续的。 (2) x(t )et dt ,其中σ为正实数,即x(t)为指数级的; 0 则可定义x(t)的拉氏变换X(s):
n n st
s n 1
1
n! u e du n 1 s
n u
L[e x(t )] X (s a)
5、延时定理:
at
L[ x(t a) 1(t a)] eas X (s)
6、初值定理:
t 0
lim x(t ) lim sX ( s )
s
7、终值定理:
lim x(t ) lim sX ( s )
分解因式,根据不同情况,利用待定系数法求反拉 氏变换
拉氏变换的运用
求解微分方程
X (s) L[ x(t )] x(t )est dt ˆ
0
式中:s为复变量;x(t)为原函数;X(s)为象函数
二、简单拉氏变换: 1、单位阶跃函数1(t) 2、指数函数 e at 3、正弦函数sinωt和余弦函数cosωt 利用欧拉公式 e j cos j sin
e j cos j sin e j e j sin 2j e j e j cos 2j
4、幂函数tn 利用Γ(gama)函数的性质:
(a ) x a 1e x dx ˆ
0
(n 1) n(n) n! u st u t s 1 dt du s L[t ] t e dt
拉普拉氏变换与反变换
一、定义: 对于函数 x(t ),如果满足下列条件: x (1)当t<0时, (t ) =0; 当t>0时,x(t)在每个有限区间上是分段连续的。 (2) x(t )et dt ,其中σ为正实数,即x(t)为指数级的; 0 则可定义x(t)的拉氏变换X(s):
n n st
s n 1
1
n! u e du n 1 s
n u
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f1 ( ) f2 (t ) d
称为函数 f1(t)与 f2(t)的卷积, 记为 f1(t)*f2(t).
即
f1(t ) f2 (t ) f1( ) f2 (t )d .
(1)
返回
结 束
第九章 拉普拉氏变换
7 June 2020 第10页
若当自变量为负时,函数值为0,则上式可 表示为:
解:根据卷积的定义,得
t
f1(t ) f2 (t )
sin(t )d
0
cos(t ) |0t
2.2 结合律
f1(t ) [ f2 (t ) f3 (t )] [ f1(t ) f2 (t )] f3 (t ).
2.3 分配律
f1(t ) [ f2 (t ) f3 (t )] f1(t ) f2 (t ) f1(t ) f3 (t ).
返回
结 束
第九章 拉普拉氏变换
7 June 2020 第12页
f (t )d t,
则
h'(t) f (t), h(0) 0.
于是 L[h'(t )] sL[h(t )] h(0) sL[h(t )],
即
t
1
1
L[ f (t)dt] L[ f (t)] F (s).
0
s
s
重复应用上式,可以得到
t
t
t
1
L[ d t d t
0
0
0 f (t )dt] sn F (s).
f (t )estdt f (t )estdt
0
f (t )estdt. 因t 时 f (t ) 0
返回
结 束
第九章 拉普拉氏变换
6、相似性质
若L[ f (t)] F(s), a 0,则
L[
f
(at )]
1
F(
s ).
aa
7 June 2020 第7页
证明:由拉氏变换的定义知
7 June 2020 第6页
5、延迟性质
若L[ f (t )] F (s), 又 t 0时 f (t) 0,则对于
任一非负实数,有
L[ f (t )] e s F (s).
或者 L1[e s F (s)] f (t ).
证明:根据定义,得
L[ f (t )] f (t )estdt 0
返回
结 束
第九章 拉普拉氏变换
7 June 2020 第3页
另外,关于像函数的积分,有如下公式:
若L[ f (t)] F (s),则
f (t)
L[ t ] s F (s)ds. (*)
f (t)
L[ tn ]
ds dsL
s
s
F (s)ds.
s
特别地,在*式中令s=0,则
f (t ) e0tdt
证明: 根据定义,得
L[es0t f (t )] e s0t f (t )e std t f (t )e(ss0 )td t
0
0
F (s s0 ), Re(s s0 ) c.
这个性质表明了一个像原函数乘以e s0t 的
拉氏变换等于其像函数作位移s0 .
返回
结 束
第九章 拉普拉氏变换
L[ f (at )] f (at)estdt 0
at u
f
su
(u)e a du
1
F(
s ).
0
aa
返回
结 束
第九章 拉普拉氏变换
7 June 2020
练习题 求下列函数的拉氏变换:
第8页
(1) f (t ) te2t cos 3t;
(2) f (t ) t t e3t sin 2t d t. 0
本讲内容小结:
主要介绍了拉氏变换的几个性质. 重点掌握 微分性质;积分性质;位移性质.
返回
结 束
第九章 拉普拉氏变换
§3 卷 积
7 June 2020 第9页
卷积是积分变换中的一个重要概念,这一运算
在实际问题如线性系统分析中有着重要应用.
下面着重介绍卷积的概念与卷积定理. 1、卷积
定义 设函数 f1(t), f2(t)在整个数轴上有定义, 则
t
0 1 f2(t )d
t 0
t 1 e (t )d
0
e t t e d 1 e t (t 0). 0
第13页
f1(t ) f2 (t ) 0 (t 0).
练习:请计算 f2 (t ) f1(t ).
返回
结 束
第九章 拉普拉氏变换Fra bibliotek7 June 2020 第14页
例2 求函数 f1(t ) t, f2 (t ) sin t 的拉氏卷积.
t
f1(t ) f2 (t ) 0 f1( ) f2 (t )d . (2)
-------拉氏变换下的卷积的定义.
注:不同变换下的卷积定义不同.
返回
结 束
第九章 拉普拉氏变换
2、卷积的性质
7 June 2020 第11页
2.1 交换律 f1(t ) f2 (t ) f2 (t ) f1(t ).
0t
0
1 s2
1
ds
arctan
|0
2
.
思考题:
sin t et dt ? 0t
返回
结 束
第九章 拉普拉氏变换
4、位移性质
7 June 2020 第5页
若L[ f (t)] F (s), 则
或者
L[es0t f (t)] F (s s0 ), Re(s s0 ) c. L1[F (s s0 )] es0t L1[F (s)] e s0t f (t ).
浙江科技学院
Zhejiang University of Science and Technology
第九章 拉普拉氏变换
返回
结 束
第九章 拉普拉氏变换
7 June 2020 第2页
3、积分性质
若L[ f (t)] F (s), 则
t
1
L[0 f (t )dt] s F (s).
证明:设
t
h(t ) 0
例1
设
f1(t)
0, 1,
t 0, t 0;
求 f1(t)*f2(t).
f1()
1
Oo
0, t 0, f2 (t ) et , t 0.
f2(t)
1
O
t
返回
结 束
第九章 拉普拉氏变换
解:代入定义,计算积分即可.
7 June 2020
t
f1(t ) f2(t ) 0 f1( ) f2 (t )d
f (t ) dt
F (s)ds.
0t
0t
0
返回
结 束
第九章 拉普拉氏变换
7 June 2020 第4页
例8 求 f (t ) sin t 的拉氏变换.
t
解:因为
L[sin t]
1 s2 1 ,
所以
L[sin t ]
t
s
1 s2
1
ds
arctan
s
|s
2
arctan
s.
于是
sin t dt
