相似三角形常见题型
相似三角形判定经典题型
相似三角形判定经典题型题型一、相似三角形判定的灵活运用例、如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③；④AC2=AD·AB。
其中单独能够判定△ABC∽△ACD的个数为[ ] A.1 B.2 C.3 D.4题型二、相似三角形判定的开放性问题例、如图，已知△ABC和△DEF，∠A=∠D=90°，且△ABC与△DEF不相似，问是否存在某种直线分割，使△ABC所分割成的两个三角形与△DEF所分割成的两个三角形分别对应相似？（1）如果存在，请你设计出分割方案，并给出证明；如果不存在，请简要说明理由；（2）这样的分割是唯一的吗？若还有，请再设计出一种．321点拨：本题主要考察对全等三角形和相似三角形的理解与应用，根据条件注意到的一个条件式，进而得到y与x的一）小题中，则要从果溯源，要使△BEH∽△BAE题型四、相似三角形的判定与性质综合运用例、如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE 。
（1）试说明BE·AD=CD·AE（2）根据图形特点，猜想可能等于哪两条线段的比?并证明你的猜想（只须写出有线段的一组即可）。
题型五、相似在实际中的应用例、如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3 米到达E处时，测得影子EF的长为2米，已知王华的身高是1.5米．（1）求路灯A的高度；（2）当王华再向前走2米，到达F处时，他的影长是多少？例2、已知零件的外径为25cm，要求它的厚度x，需先求出它的内孔直径AB，现用一个交叉卡钳(AC和BD的长相等)去量(如图)，若OA：OC=OB：OD=3，CD=7cm．求此零件的厚度x．题型六、相似方案的设计如图，已知Rt△ABC与△DEF不相似，其中∠C、∠F为直角，能否分别将这两个三角形各分割成两个三角形，使△ABC所分成的每个三角形与△DEF所分成的每个三角形分别对应相似？如果能，请设计出一种分割方案，并说明理由。
完整版)相似三角形题型归纳
完整版)相似三角形题型归纳1、在平行四边形ABCD中，点E为对角线AC上的一点，且AE∶EC=1∶3.将BE延长至与CD的延长线交于点G，与AD交于点F。
证明BF∶FG=1∶2.2、在直角三角形ABC中，∠BAC=90°，AB=AC，D为BC的中点，E为AC上的一点。
点G在BE上，连接DG并延长至交AE于点F，且∠FGE=45°。
证明：（1）BD·BC=BG·BE；（2）AG⊥BE；（3）若E为AC的中点，则EF∶FD=1∶2.3、在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上的一点，连接BO交AD于点F，OE⊥OB交BC边于点E。
证明：（1）△ABF∽△COE；（2）当O为AC的中点时，求△ABC的面积；（3）当O为AC边中点时，求△ABC的面积。
4、在平行四边形ABCD和平行四边形ACED中，点R为DE的中点，BR分别交AC、CD于点P、Q。
写出各对相似三角形（相似比为1除外），并求出BP∶PQ∶QR的值。
5、在△ABC中，AD平分∠BAC，EM为AD的中垂线，交BC延长线于点E。
证明DE=BE·CE。
6、过△ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和E。
证明AE∶ED=2AF∶FB。
7、在Rt△ABC中，CD为斜边AB上的高，点M在CD 上，DH⊥BM且与AC的延长线交于点E。
证明：（1）△AED∽△CBM；（2）DE=DM。
8、在△ABC中，BD、CE分别是两边上的高，过D作DG⊥BC于点G，分别交CE及BA的延长线于点F、H。
证明：（1）DG＝BG·CG；（2）BG·CG＝GF·GH。
9、在平行四边形ABCD中，点P为对角线AC上的一点。
过P的直线与AD、BC、CD的延长线、AB的延长线分别相交于点E、F、G、H。
证明：AG∶GB=CP∶PD。
1、求证：如图，已知平行四边形ABCD中，点P在AC上，点Q在BC上，且AP=CQ。
相似三角形经典题型
相似三角形经典题型一、相似三角形的判定定理相关题型1. 题目已知在△ABC和△A'B'C'中，∠A = 50°，AB = 3cm，AC = 4cm，∠A'= 50°，A'B'= 6cm，A'C' = 8cm。
判断这两个三角形是否相似。
解析根据相似三角形的判定定理：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。
在△ABC和△A'B'C'中，(AB)/(A'B')=(3)/(6)=(1)/(2)，(AC)/(A'C')=(4)/(8)=(1)/(2)，且∠A = ∠A' = 50°。
所以△ABC∽△A'B'C'。
2. 题目如图，在四边形ABCD中，∠B = ∠ACD，AB = 6，BC = 4，AC = 5，CD=(7)/(2)，求AD的长。
解析因为∠B = ∠ACD，且(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，(AC)/(AD)未知。
又因为(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，不满足三边对应成比例。
但是由∠B = ∠ACD，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，可以尝试证明△ABC和△ACD相似。
因为∠B = ∠ACD，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，这里我们重新计算(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)是错误的，应该是(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(BC)/(CD)所以△ABC∽△DCA。
相似三角形常考题型
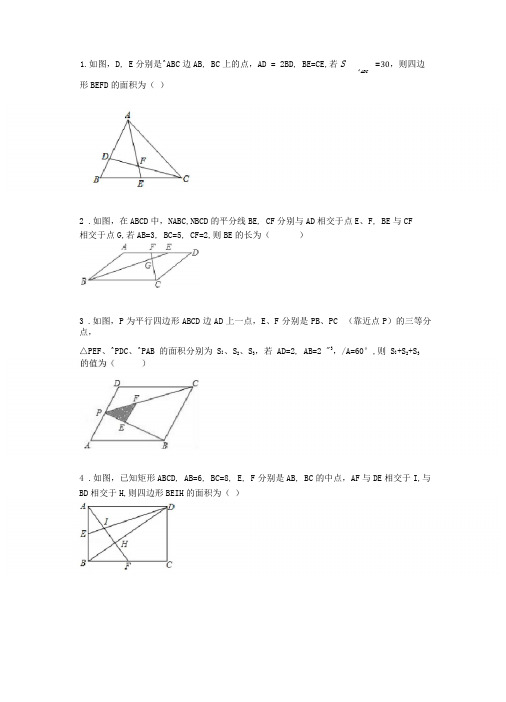
2 .如图，在ABCD 中，NABC,NBCD 的平分线BE, CF 分别与AD 相交于点E 、F, BE 与CF 相交于点G,若AB=3, BC=5, CF=2,则BE 的长为（ ）3 .如图，P 为平行四边形ABCD 边AD 上一点，E 、F 分别是PB 、PC （靠近点P ）的三等分点，△PEF、^PDC 、^PAB 的面积分别为 S ]、S 2、S 3，若 AD=2, AB=2 "3，/A=60°,则 S ]+S 2+S 34 .如图，已知矩形ABCD, AB=6, BC=8, E, F 分别是AB, BC 的中点，AF 与DE 相交于I,与 BD 相交于H,则四边形BEIH 的面积为（ ）1.如图，D, E 分别是^ABC 边AB, BC 上的点，AD = 2BD, BE=CE,若S ^ABC =30，则四边形BEFD 的面积为（ ）5.如图，DE是AABC的中位线，M是DE的中点，CM的延长线交AB于点N,则S^^： S四边形从顺等于( )6.如图，在4ABC中，AB=AC=1, BC=上，在AC边上截取AD=BC,连接BD.2(1)通过计算，判断AD 2与AC-CD的大小关系;(2)求NABD的度数.7.如图4, 4ABC与ADEF均为等边三角形，O为BC、EF的中点，则UAD： BE的值为()8.如图，已知4ABC是面积为,：M的等边三角形，4ABC S A ADE, AB=2AD,Z BAD=45°, ACAFAC 交于点F,则CF 的值为（）10.如图，矩形ABCD 中，AB=3, BC=4,动点P 从A 点出发，按A-B-C 的方向在AB 和BC 上移动，记PA=x ，点D 到直线PA 的距离为y,则y 关于x 的函数图象大致是（）11 .如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动， 然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个 三角形重叠面积为y,则y 关于x 的函数图象是（ ）与DE 相交于点F ,则dEF 的面积等于 （结果保留根9.如图，4ABC 中，AB=AC, D 为BC 中点，在BA 的延长线上取一点E,使得ED=EC, ED 与A12.如图，菱形ABCD中，AB=AC,点E、F分别为边AB、BC上的点，且AE=BF,连接CE、AF 交于点H，连接DH交AG于点O.则下列结论①△ABF04CAE,②NAHC=120°,③AH+CH=DH,④AD2=OD-DH中，正确的是______ .13.如图，在矩形ABCD中，AD=6, AELBD,垂足为E, ED=3BE,点P、Q分别在BD, AD上，则AP+PQ的最小值为()B C14.如图，在矩形ABCD中，AC与BD相交于O,NCOD=6O°,点E是BC边上的动点，连结DE,OE．(1)求证：ACOD是等边三角形；(2)如图1,当DE平分NADC时，试证明OC二EC,并求出NDOE的度数;（3）如图2,当DE平分NBDC时，试证明0E2 + OD2 = DE2.15.问题背景已知在4ABC中，AB边上的动点D由A向B运动（与A、B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于点F，点H是线段AF上一点.小王同学发现可以由以下两种思路解决问题： 思路一：过点D 作DG 〃BC,交AC 于点G,先证GH 二AH,再证GF 二CF,从而证得结论成立； 思路二：过点E 作EMLAC,交AC 的延长线于点M,先证CM 二AH,再证HF 二MF,从而证得结论 成立.请你任选一种思路，完整地书写本小题的证明过程(如用两种方法作答，则以第一种方法评 分)；(2)类比探究 _ 如图2,若在4ABC 中，ZABC=90°, ZADH=ZBAC=30°,且点D, E 的运动速度之比是■；工 1,求磐的值；Hi 1(3)延伸拓展 如图3,若在4ABC 中，AB=AC,NADH=NBAC=36°,记H_=m,且点D, E 的运动速度相等，AC试用含m 的代数式表示器(直接写出结果，不必写解答过程).Hi 1且点D, E 的运动速度相等.求证：HF=AH+CF. 如图1,若4ABC 是等边三角形，DHXAC,。
相似三角形题型
相似三角形题型
相似三角形是初中数学中非常重要的一部分，以下是一些常见的相似三角形题型：
1. **利用相似三角形求长度**。
在这种题型中，通常会给出一个或多个相似三角形，并询问某个特定边的长度。
解决此类问题通常需要找出相似三角形的对应边，并利用其比例关系来求解。
2. **利用相似三角形求角度**。
这类问题通常会涉及一个或多个相似三角形的角度。
通过相似三角形的对应角相等这一性质，可以很容易地求解出未知角度。
3. **利用相似三角形求面积**。
根据相似三角形的面积比等于对应边的平方比这一性质，我们可以通过已知的相似三角形面积来求出未知的相似三角形面积。
4. **利用相似三角形设计问题**。
这类问题通常会设计一个实际问题场景，例如建筑设计、机械设计等，然后通过引入相似三角形来解决这个问题。
5. **利用相似三角形解决实际问题**。
例如，在物理学中，可以利用相似三角形来解决一些力学问题；在地理学中，可以利用相似三角形来计算一些地理数据等。
以上只是相似三角形题型的部分例子，实际上，相似三角形的应用非常广泛，可以用来解决很多实际问题。
在解决相似三角形问题时，一定要灵活运用相似三角形的性质和定理，以及相关的数学知识和方法。
三角形相似题型大全
三角形相似题型大全
三角形相似是数学几何中的一个重要概念，涉及到的题型非常多样。
以下是几种常见的三角形相似题型：
1. 平行线型：当两条平行线被第三条线段所截，所形成的三角形是相似的。
这是三角形相似的一个基本题型。
2. 角相等型：当两个三角形中有两个对应的角相等时，这两个三角形是相似的。
这也是一个比较常见的题型。
3. 边长比例型：当两个三角形的对应边长之间存在一定的比例关系时，这两个三角形是相似的。
这种题型在解决实际问题时经常出现。
4. 综合型：结合以上几种情况，可能需要在多个条件下判断三角形是否相似。
这种题型较为复杂，需要综合考虑各种因素。
在解决三角形相似问题时，需要灵活运用三角形相似的判定定理和性质定理，同时结合题目给出的条件进行推理和计算。
此外，对于一些比较复杂的题型，可能需要采用一些特殊的解题方法，如代数法、几何法等。
希望这些题型能够帮助你更好地理解和掌握三角形相似的知识，提高解决实际问题的能力。
三角形相似经典题型归类
盐城中学八年级数学教研组 相似典型题目三角形相似典型题目主备、审核人：盐城市初级中学教研组1、如图，AC ∥DB ，AB 、CD 相交于点O 。
过点O 的直线交AC 于点E ，交DB 于点F 。
写出图中所有相似三角形及其对应边所组成的比例式，并说明理由。
2、如图，AB ∥A ’B ’，BC ∥B ’C ’。
△AOC 与△A ’OC ’相似吗？为什么？3、如图O 是△ABC 内任意一点，A ’、B ’、C ’分别是OA 、OB 、OC 的中点。
△A ’B ’C ’与△ABC 相似吗？为什么？4、如图，点B 、D 、F 、E 在一条直线上， = = 。
（1）△ABC 与△ADE 是否相似？为什么？ （2）若∠BAD=18°,求∠FBC 的度数。
5、如图，在平行四边形ABCD 中，点F 在BA 的延长线上，CF 、AD 相交于点E 。
（1）△CDE 与△FAE 相似吗？为什么？（2）当E 是AD 的中点，且BC=2CD ，∠F 与∠BCF 有怎样的数量关系？为什么？A EF B D O CC B B ’ C ’ O AA ’ A O A ’’ C ’C B ’ B AD AB DE BC AC AEC F E DBA B FE D C A共4页第-1-页6、暑假小明和家人一起去海南岛玩，小明发现沙滩上有许多椰子树。
于是小明想利用椰子树树荫测树高，他在某一时刻测得的直立的标杆高1m 时，影长0.8m ，同时测树影时，因树靠近建筑物，影子的一部分落在墙面上（如图），若此时树在地面上的影长为5.2m,在墙上的影高1.5m ，求树高。
7、如图小军想出了一个测量建筑物高度的方法:在地面上C 处平放一面镜子,并在镜子上做一个标记,然后向后退去,直至看到建筑物的顶端A 在镜子中的象与镜子上 的标记重合.如果小军的眼睛距地面1.65m,BC 、CD 的长分别为60m 、3m,求这座建筑物的高度为多少？8、如图，零件的外径为16cm ，要求它的壁厚x ，需要先求出内经AB ，先用一个交叉钳（AD 与BC 相等）去量，若测得OA ：OD=OB ：OC=3：1，CD=5cm ，你能求零件的壁厚x 吗？9、如图已知：AB=4、BC=2 (1)求当AD=？时△ACD ∽△ABC (2)求当CE=？时△AED ∽△ABC共4页第-2-页DBCA EBAαα CDE∅16A BC DOBACE10、如图在□ABCD 中E 为BC 中点F 为CD 四等分点(1)说明AE ⊥EF 。
相似三角形性质完整的题型+答案
相似三角形性质知识精要一、相似三角形的性质1、(定义):相似三角形的对应角相等，对应边成比例。
2、性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
3、性质定理2:相似三角形的周长比等于相似比。
4、性质定理3:相似三角形的面积比等于相似比的平方。
二、相似三角形的应用例题讲解:例题:地图比例尺为1:2000，一块多边形地区在地图上周长为50cm，面积为100cm2，实际周长为1000 m，实际面积为40000m2。
变式:东海大桥全长32.5千米，如果东海大桥在某张地图上的长为6.5厘米，那么该地图上距离与实际距离的比为( )。
A.1:5000000B.1:500000C.1:50000D.1:5000答案：B例题:(1)两个相似三角形的面积之比为9:16，它们的对应高之比为3:4 。
(2)两个相似三角形的相似比为1:3，则它们的周长比为1:3 ，面积比为1:9 。
变式:(1)两个相似三角形面积之比是1:3，则他们对应边上的高之比为( )。
(A).1:3 (B) 3:1 (C) 1:3(D) 1:9(2)两个相似三角形的相似比是2:3，面积相差30厘米2，则它们的面积之和是( )。
(A)150厘米2(B) 65厘米2(C) 45厘米2(D) 78厘米2答案：(1) C (2)D。
例题:如图，已知DE//BC ，AD:DB=2:3，那么S △ADE :S △ECB = 4:15 。
变式:如图，在ABCD 中，AC 与DE 交于点F ，AE:EB=1:2，S △AEF =6cm 2，则S △CDF 的值为( )。
A.12cm 2B.15cm 2C.24cm 2D.54cm 2答案：D 。
例题:如图，已知梯形ABCD 中，AD//BC ，AD:BC=3:5， 求: (1)S △AOD :S △BOC 的值；(2)S △AOB :S △AOD 的值. 答案:(1)9:25 (2)5:3。
相似三角形的判定十大题型
在△BPG 中，∵∠B＝45°，
∴∠AGB＝∠CPF，
∴∠BPG+∠BGP＝135°，
∵∠B＝∠C，
∴∠BGP＝∠CPF，
∴△PBG∽△FCP．
∵∠B＝∠C，
∴△PBG∽△FCP；
【题型4 利用相似三角形的判定探究线段之间的关系】
【例 4】四边形 ABCD 中，点 E 在边 AB 上，连接 DE，CE． （1）若∠A＝∠B＝∠DEC＝50°，找出图中的相似三角形，并说明理由； （2）若四边形 ABCD 为矩形，AB＝5，BC＝2，且图中的三个三角形都相似，求 AE 的 长． （3）若∠A＝∠B＝90°，AD＜BC，图中的三个三角形都相似，请判断 AE 和 BE 的数 量关系并说明理由．
解：（1）∵D、E 分别是 AC、BC 的中点， ∴DE∥AB，DE= 12AB＝5， ∵DE∥AB， ∴∠DEC＝∠B，而∠F＝∠B， ∴∠DEC＝∠F， ∴DF＝DE＝5； （2）∵AC＝BC， ∴∠A＝∠B， ∵∠CDE＝∠A，∠CED＝∠B， ∴∠CDE＝∠B， ∵∠B＝∠F， ∴∠CDE＝∠F， ∵∠CED＝∠DEF， ∴△CDE∽△DFE．
出发，问在运动 5 秒钟内，以点 D，A，E 为顶点的三角形何时与△OCD 相似？（只考
虑以点 A、O 为对应顶点的情况）
解：（1）C（3，4），D（9，4）；
（2）易知：OB＝AB＝10；
∵C 点坐标为（3，4），
∴点 C 到 x 轴的距离为 4
①当点 D 在线段 OA 上，即 0＜t≤6 时，OD＝2t；
则：S=
12OD×4=
1 2
×2t×4＝4t；
②当 D 在线段 AB 上，即 6≤t＜11 时，BD＝OA+AB﹣2t＝22﹣2t；
相似三角形的判定与性质(六大类型)(题型专练)(原卷版)
专题02 相似三角形的判定与性质（六大类型）【题型1 相似三角形的概念】【题型2 三边对应成比例，两三角形相似】【题型3两边对应成比例且夹角相等，两三角形相似】【题型4 两角对应相等，两三角形相似】【题型5 相似三角形的性质】【题型6相似三角形的性质与判定综合应用】【题型1 相似三角形的概念】1．（2023春•阳信县月考）下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则在网格图中的三角形与△ABC相似的是（）A．B．C．D．2．（2022秋•道外区期末）下列三角形一定相似的是（）A．两个等腰三角形B．两个等边三角形C．两个直角三角形D．有一角为70°的两个等腰三角形3．（2022秋•武城县期末）下列两个图形：①两个等腰三角形；②两个直角三角形；③两个正方形；④两个矩形；⑤两个菱形；⑥两个正五边形．其中一定相似的有（）A．2组B．3组C．4组D．5组4．（2022秋•承德县期末）如图所示，网格中相似的两个三角形是（）A．①与②B．①与③C．③与④D．②与③5．（2022秋•襄都区校级期末）下列判断中，不正确的有（）A．三边对应成比例的两个三角形相似B．两边对应成比例，且有一个角相等的两个三角形相似C．斜边与一条直角边对应成比例的两个直角三角形相似D．有一个角是100°的两个等腰三角形相似【题型2 三边对应成比例，两三角形相似】6．（2022秋•常州期末）如图，△ABC∽△DEF，则DF的长是（）A．B．C．2D．3 7．（2023•陇南模拟）两个相似三角形的相似比是4：9，则其面积之比是（）A．2：3B．4：9C．9：4D．16：81 8．（2023•沙坪坝区校级模拟）如图，△ABO∽△CDO，若BO＝6，DO＝3，AB＝4，则CD的长是（）A．1B．2C．3D．49．（2022秋•鼓楼区期末）已知△ABC∽△DEF，若△ABC的三边分别长为6，8，10，△DEF的面积为96，则△DEF的周长为．10．（2023•惠城区校级一模）若△ABC∽△DEF，△ABC的面积为81cm2，△DEF的面积为36cm2，且AB＝12cm，则DE＝cm．11．（2022秋•于洪区期末）两个相似三角形的周长比是3：4，其中较小三角形的面积为18cm2，则较大三角形的面积为cm2．12．（2022秋•鸡西期末）如果两个相似三角形的周长比为1：6，那么这两个三角形的面积比为．13．（2023•长宁区一模）如果两个相似三角形的面积比是1：9，那么它们的周长比是．14．（2022秋•内乡县期末）如图，已知△ABC∽△ADE，AD＝6，BD＝3，DE ＝4，则BC＝．15．（2022秋•零陵区期末）若△ABC∽△A′B′C′，且，△ABC 的面积为12cm2，则△A′B′C′的面积为cm2．【题型3两边对应成比例且夹角相等，两三角形相似】16．（2022秋•仓山区校级月考）如图，D、E分别是△ABC的边AB、AC上的点，AB＝8，BD＝5，AC＝6，CE＝2，求证：△ADE∽△ACB．17．（2021秋•武陵区期末）如图，已知∠BAE＝∠CAD，AB＝18，AC＝48，AE＝15，AD＝40．求证：△ABC∽△AED．18．（2022秋•丰泽区校级期中）如图，E是△ABC的边BC上的点，已知∠BAE ＝∠CAD，，AB＝18，AE＝15．求证：△ABC∽△AED．19．（2022春•丰城市校级期末）如图，已知∠B＝∠E＝90°，AB＝6，BF＝3，CF＝5，DE＝15，DF＝25．求证：△ABC∽△DEF．【题型4 两角对应相等，两三角形相似】20．（2022秋•蚌山区月考）已知：如图D、E分别是△ABC的边AB、AC上的点，∠A＝40°，∠C＝80°，∠AED＝60°，求证：△ADE∽△ACB．21．（2022秋•龙胜县期中）如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的高．求证：△ABC∽△CBD．22．（2022•江夏区模拟）如图，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD．求证：△ABC∽△DEC．23．（2021秋•晋江市校级期末）如图，在△ABC中，点D在BC边上，点E在AC边上，且AD＝AB，∠DEC＝∠B．求证：△AED∽△ADC．24．（2022•南昌模拟）如图，在△ABC中，∠A＝36°，AB＝AC，BD是∠ABC 的平分线．求证：△ABC∽△BDC．【题型5 相似三角形的性质】25．（2020秋•思南县校级月考）判断图中的两个三角形是否相似，并说明理由．26．（大观区校级期中）如图，在边长为1的小正方形组成的网格中，△ABC 和△DEF的顶点都在格点上，请判断△ABC和△DEF是否相似，并说明理由．【题型6相似三角形的性质与判定综合应用】27．（2022秋•历城区校级月考）如图，AB∥CD，AC与BD交于点E，且AB＝4，AE＝2，AC＝8．（1）求CD的长；（2）求证：△ABE∽△ACB．28．（2023•殷都区一模）如图，O是直线MN上一点，∠AOB＝90°，过点A 作AC⊥MN于点C，过点B作BD⊥MN于点D．（1）求证：△AOC∽△OBD；（2）若OA＝5，OC＝OD＝3，求BD的长．29．（2023•西湖区校级二模）如图，在菱形ABCD中，点M为对角线BD上一点，连接AM并延长交BC于点E，连接CM．（1）求证：CM＝AM．（2）若∠ABC＝60°，∠EMC＝30°，求的值．30．（2023•港南区四模）如图，在△ABC中，D在AC上，DE∥BC，DF∥AB．（1）求证：△DFC∽△AED；（2）若CD＝AC，求的值．31．（2023春•鼓楼区校级期末）如图，点C是△ABD边AD上一点，且满足∠CBD＝∠A．（1）证明：△BCD∽△ABD；（2）若BC：AB＝3：5，AC＝16，求BD的长．32．（2022秋•顺平县期末）矩形ABCD中，E为DC上的一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F．（1）求证：△ABF∽△FCE；（2）若AB＝4，AD＝8，求CE的长．33．（2022秋•南京期末）如图，在矩形ABCD中，点E，F分别在边BC，CD 上，AE，BF交于点G．（1）若＝，求证AE⊥BF；（2）若E，F分别是BC，CD的中点，则的值为．34．（2023•桐乡市校级开学）如图，已知△ABC和△AED，边AB，DE交于点F，AD平分∠BAC，AF平分∠EAD，．（1）求证：△AED∽△ABC；（2）若BD＝3，BF＝2，求AB的长．35．（2022秋•海陵区校级期末）如图，矩形DEFG的四个顶点分别在等腰三角形ABC的边上．已知△ABC的AB＝AC＝10，BC＝16，记矩形DEFG的面积为S，线段BE为x．（1）求S关于x的函数表达式；（2）当S＝24时，求x的值．36．（2022秋•平城区校级期末）如图，已知在△ABC中，边BC＝6，高AD＝3，正方形EFGH的顶点F，G在边BC上，顶点E，H分别在边AB和AC上，求这个正方形的边长．。
初三数学相似三角形经典题型
初三数学相似三角形经典题型
以下是关于初三数学相似三角形的经典题型：
1. 题目：在△ABC中，∠BAC=60°，AB=2，AC=1，D是BC上一点，向量AD=x倍的向量AB加上y倍的向量AC，且x+y=1，则AD的长度的最小值为 _______．
2. 题目：在△ABC中，AB = 3，AC = 4，∠BAC = 60°，若 P 是 BC 边上的一个动点，且ΔABP 与∆ABC 相似，则 AP 的最小值为 _______．
3. 题目：在△ABC中，AB = AC，D是BC上一点，∠BAC = 120°，则
AD/AB 的值为 _______．
4. 题目：已知：$A,H,B,C,D,E,F$七点中的每三个点都不在一条直线上，从这七点中选三个点连成三角形．一共可以画出$42$个三角形(当这七点排成一条直线时，可以构成$3$个三角形)，其中有几条与线段BC构成等腰三角形？
5. 题目：在△ABC中，∠BAC = 60°，AB = 2，AC = 1，D是BC上一点，向量AD = x倍的向量AB + y倍的向量AC (x + y = 1)，则向量AD模的最小值为 _______．
以上题目均考察了相似三角形的性质和判定方法。
解决这类问题时，需要灵活运用相似三角形的性质和判定定理。
相似三角形的性质定理(3种题型)-2023年新九年级数学核心知识点与常见题型(沪教版)(解析版)
相似三角形的性质定理（3种题型）【知识梳理】一、相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比． 二、相似三角形性质定理2相似三角形周长的比等于相似比． 三、相似三角形性质定理3相似三角形的面积的比等于相似比的平方．【考点剖析】题型一：相似三角形性质定理1例1.已知ABC ∆∽111A B C ∆，顶点A 、B 、C 分别与A 1、B 1、C 1对应，1132AB A B =，BE 、B 1E 1分别是它们的对应中线，且6BE =．求B 1E 1的长． 【答案】4．【解析】解：111ABC A B C ∆∆∽，BE 、11B E 分别是对应中线，1111AB BEA B E B ∴=即11362E B =，114E B =【总结】本题考查相似三角形对应中线的比等于相似比．例2.已知ABC ∆∽111A B C ∆，顶点A 、B 、C 分别与A 1、B 1、C 1对应，12AC =，119A C =,1A ∠的平分线A 1D 1的长为6，求A ∠的平分线的长． 【答案】8．【解析】解：111ABC A B C ∆∆∽，AD 、11A D 分别是A ∠、1A ∠的平分线，1111AC AD A C A D ∴=即1296AD =，8AD ∴=即A ∠的平分线的长为8．【总结】本题考查相似三角形对应角平分线的比等于相似比． 例3.求证：相似三角形对应高的比等于相似比．【解析】已知：如图，111ABC A B C ∆∆∽，且相似比为k ，AD 、11A D 分别是BC 、11B C 的高．求证：11ADkA D =．证明：111ABC A B C ∆∆∽，1B B ∴∠=∠，11ABkA B =；又AD 、11A D 分别是BC 、11B C 的高，11190BDA B D A ∴∠=∠=，111ABD A B D ∴∆∆∽，1111AB ADk A B A D ∴==．【总结】本题考查相似三角形的判定和性质． 例4.求证：相似三角形对应中线的比等于相似比．【解析】已知：如图，111ABC A B C ∆∆∽，且相似比为k ，AD 、11A D 分别是边BC 、11B C 的 中线．求证： 11ADk A D =．证明：111ABC A B C ∆∆∽，1B B ∴∠=∠，1111AB CBkA B C B ==；又AD 、11A D 分别是边BC 、11B C 的中线，12BD BC ∴=，111112B D B C =，∴11DB k D B =，1111AB BD A B B D ∴=，111ABD A B D ∴∆∆∽，1111AB ADkA B A D ∴==．【总结】本题考查相似三角形的判定和性质的运用．例5.求证：相似三角形对应角平分线的比等于相似比．【解析】已知：如图，111ABC A B C ∆∆∽，且相似比为k ，AD 、11A D 分别是BAC ∠、111B A C ∠ 的角平分线．求证：11ADk A D =．证明：111ABC A B C ∆∆∽，1B B ∴∠=∠，111BAC B A C ∠=∠，11ABkA B =；又AD 、11A D 分别是BAC ∠、111B A C ∠的角平分线，11111111,22BAD BAC B A D B A C ∴∠=∠∠=∠，111BAD B A D ∴∠=∠，111ABD A B D ∴∆∆∽，1111AB ADk A B A D ∴==．【总结】本题考查相似三角形的判定和性质．例 6.如图，ABC ∆和111A B C ∆中，AD 和BE 是ABC ∆的高，11A D 和11B E 是111A B C ∆的高，且1C C ∠=∠，1111AD ABA D AB =． 求证：1111AD BEA DB E =【解析】AB C D EA 1E 1D 1 C 1B 1证明：1111AB ADA B A D =，又111ADB A D B ∠=∠，111ABD A B D ∴∆∆∽，111ABD A B D ∴∠=∠，又1C C ∠=∠，111ABC A B C ∴∆∆∽，又BE 、11B E 分别是ABC ∆、111A B C ∆的高，1111BE AB E B A B ∴=，1111BE ADE B A D ∴=．【总结】本题考查相似三角形的判定和性质的综合运用．例7.如图，D 是ABC ∆的边BC 上的点，BAD C ∠=∠，BE 是ABC ∆的角平分线，交AD 于点F ，1BD =，3CD =，求BF ：BE ．【解析】解：BE 是ABC ∆的角平分线，∴ABF EBC ∠=∠，又BAD C ∠=∠，ABF CBE ∴∆∆∽，AB BFCB BE ∴=，又BAD C ∠=∠，ABD ABC ∠=∠BAD BCA ∴∆∆∽，AB BD BC BA ∴=，14AB AB ∴=，2AB ∴=，12AB BC ∴=，1:2BF BE ∴=．【总结】本题考查相似三角形的判定和性质的综合运用．例8.如图，在ABC ∆中，矩形DEFG 的一边DE 在BC 边上，顶点G 、F 分别在AB 、AC 边上，AH 是BC 边上的高，AH 与GF 交于点K ．若32AH cm =，48BC cm =，矩形DEFG 的周长为76cm ，求矩形DEFG 的面积．【答案】2360cm ．AB C DEFABC D EFGH K【解析】解：设DG xcm =，()38FG x cm=−矩形DEFG ，//90GF BC GDB ∴∠=，，GF AGBC AB ∴=,又AH 是高，90AHB ∴∠=，GDB AHB ∴∠=∠//DG AH ∴,DG BG AH AB ∴=，1DG GFAH BC ∴+=,3813248x x −∴+=，20x ∴=，∴20DG cm =，18FG cm =，2360DEFG S cm ∴=矩形． 【总结】本题考查三角形一边的平行线定理，矩形的周长面积等知识．例9.如图，正方形DEFG 的边EF 在ABC ∆的边BC 上，顶点D 、G 分别在边AB 、AC 上，AH 是ABC ∆的高，BC = 60厘米，AH = 40厘米，求正方形DEFG 的边长．【答案】24．【解析】设正方形EFGD 的边长为x ，//DG BC ，DG AD APBC AB AH ∴==．406040x x −∴=，24x ∴=，∴正方形EFGD 的边长为24．【总结】本题考查三角形内接正方形的相关知识，主要还是通过比例相等来列式建立关系． 例10.在锐角∆ABC 中，矩形DEFG 的顶点D 在AB 边上，顶点E 、F 在BC 边上，顶点G 在AC 边上，如果矩形DEFG 的长为6，宽为4，设底边BC 上的高为x ，∆ABC 的面积为y ，求y 与x 的函数关系式．ABCDEF GH P【答案】23(4)4x y x x =>−．【解析】解：如图， 矩形DEFG ，//90GD BC DEC ∴∠=，，GD AD BC AB ∴=．又 AH 是高，90AHC ∴∠=． DEC AHC ∴∠=∠， //DE AH ∴，DE BDAH AB ∴=， 1DG DEBC AH ∴+=， 641BC x ∴+=，64xBC x ∴=−，又12ABC S y BC AH ∆==，∴()2344x y x x =>−．【总结】本题考查三角形一边的平行线定理，矩形的面积等知识．题型二：相似三角形性质定理2例11.若ABC ∆∽DEF ∆，ABC ∆与DEF ∆的相似比为1:2，则ABC ∆与DEF ∆的周长比为( )（A ）1:4 （B ）1:2 （C ）2:1 （D ）1:2【答案】B【总结】相似三角形的周长比等于相似比．例12.已知ABC ∆∽111A B C ∆，顶点A 、B 、C 分别与A 1、B 1、C 1对应，它们的周长分别为48和60，且12AB =，1125B C =，求BC 和A 1B 1的长．【答案】112015BC A B ==，．【解析】解：111ABC A B C ∆∆∽，1111111ABC A B C C AB CBC A B C B ∆∆∴==；又111484605ABC A B C C C ∆∆==，∴1120,15BC A B ==．【总结】本题考查相似三角形的性质．例13.如果两个相似三角形的最长边分别为35厘米和14厘米，它们的周长相差60厘米，那么大三角形的周长是．【答案】100cm ．【解析】两三角形的相似比为5:2，则周长比为5:2，设大三角形周长为5acm ，小三 角形周长为2acm ，则5260a a −=，所以20a =，所以大三角形的周长为100cm ． 【总结】相似三角形的周长比等于相似比．例14.如图，在ABC ∆中，12AB =，10AC =，9BC =，AD 是BC 边上的高．将ABC ∆沿EF 折叠，使点A 与点D 重合，则DEF ∆的周长为．【答案】312．【解析】由折叠得EF 垂直平分AD ，AD 是BC 上的高，ABCD EF//EF BC ∴，AEF ABC ∴∆∆∽，12AEF ABC C C ∆∆∴=，9101231ABC C ∆=++=，312AEF C ∆∴=．【总结】本题考查相似三角形的性质和判定．例15.如图，梯形ABCD 的周长为16厘米，上底3CD =厘米，下底7AB =厘米，分别延长AD 和BC 交于点P ，求PCD ∆的周长．【答案】152cm ．【解析】解：梯形ABCD ，//CD AB ∴，AEF ABC ∴∆∆∽，37PDC PAB C CD C AB ∆∆∴==，即327PDC PDC ABCD C C C CD ∆∆=+−梯形， 31667PDC PDC C C ∆∆∴=+−，152PDC C cm ∆∴=．【总结】本题考查相似三角形的性质和判定．例16.如图，在ABC ∆中，=90C ∠︒，5AB =，3BC =，点P 在AC 上（与点A 、C 不重合），点Q 在BC 上，PQ //AB ．当PQC ∆的周长与四边形P ABQ 的周长相等时，求CP 的长．【答案】247．【解析】解：CPQ PABQC C ∆=四边形，ABCD PABCPQCP CQ PQ BQ PQ AP AB ∴++=+++， CP CQ BC CQ AC CP AB ∴+=−+−+， 5AB =，3BC =，90C ∠=，4AC ∴=，345CP CQ CQ CP ∴+=−+−+，6CP CQ ∴+=，//PQ AB ，CP CQCA CB ∴=，∴643CP CP −=，247CP =． 【总结】本题考查了三角形一边的平行线性质，主要考查了学生的推理能力．题型三：相似三角形性质定理3例17.（1）如果把一个三角形的三边的长扩大为原来的100倍，那么这个三角形的面积扩大为原来的倍；（2）如果一个三角形保持形状不变但面积扩大为原来的100倍，那么这个三角形的边长扩大为原来的倍．【答案】（1）10000；（2）10．【总结】相似三角形的面积比等于相似比的平方．例16.两个相似三角形的面积分别为5cm 2和16cm 2，则它们的对应角的平分线的比为（ ）（A ）25:256（B ）5:16（C ）5:4（D ）以上都不对．【答案】C【解析】相似三角形对应角平分线的比等于相似比，对应面积的比等于相似比的平方． 【总结】本题考查相似三角形的性质．例18.如图，点D 、E 分别在ABC ∆的边AB 和AC 上，DE //BC ，6DE =，9BC =，16ADE S ∆=．求ABC S ∆的值．【答案】36．ABCD E【解析】解：//DE BC ，ADE ABC ∴∆∆∽，226499ADE ABC S DE S BC ∆∆⎛⎫⎛⎫∴=== ⎪ ⎪⎝⎭⎝⎭，36ADE S ∆∴=． 【总结】本题考查相似三角形的判定及性质．例19.如图，在ABC ∆中，D 是AB 上一点，若B ACD ∠=∠，4AD cm =，6AC cm =，28ACD S cm ∆=，求ABC ∆的面积．【答案】218cm ．【解析】解：B ACD ∠=∠，A A ∠=∠，ACD ABC ∴∆∆∽，222439ACD ABC S AD S AC ∆∆⎛⎫⎛⎫∴=== ⎪ ⎪⎝⎭⎝⎭， 又28ACD S cm ∆=，218ABC S cm ∆∴=．【总结】本题考查相似三角形的判定及性质．例20.如图，在ABC ∆中，点D 、E 在AB 、AC 上，DE //BC ，ADE ∆和四边形BCED 的面积相等，求AD :BD 的值．【答案】21+．ABCDABCD E【解析】解：//DE BC ，ADE ABC ∴∆∆∽，2ADE ABC S AD S AB ∆∆⎛⎫∴= ⎪⎝⎭，ADE BCEDS S ∆=四边形，12ADE ABC S S ∆∆∴=，12AD AB ∴=，12121AD DB ∴==+−．【总结】本题考查相似三角形的判定及性质．例21.如图，在ABC ∆中，AD BC ⊥，BE AC ⊥，D 、E 分别为垂足．若60C ∠=︒，1CDE S ∆=，求四边形DEAB 的面积．【答案】3． 【解析】解：AD BC BE AC ⊥⊥，，90CDA BEC ∴∠=∠=．90CDA BEC ∴∠=∠=，CBE CAD ∴∆∆∽，CD CACE CB ∴=．90CDA BEC ∴∠=∠=，CBE CAD ∴∆∆∽，CD CACE CB ∴=，DCE ACB ∴∆∆∽，2DCE ACB S CD S CA ∆∆⎛⎫∴= ⎪⎝⎭，又60C ∠=， 30CBE CAD ∴∠=∠=，12CD CA =，14DCE ACB S S ∆∆∴=，13DCE BDEA S S ∆∴=四边形，1CDE S ∆=，3DEAB S ∴=四边形．【总结】本题考查相似三角形的性质及判定，直角三角形的性质等知识．例22.如图，Rt ABC ∆中，点D 是BC 延长线上一点，直线EF //BD 交AB 于点E ， 交AC 于点G ，交AD 于点F ，若13AEG EBCG S S ∆=四边形，求CFAD的值．A B CDEF【答案】21．【解析】解：//EF BD ，AEG AEC ∴∆∆∽，AE AFAB AD ∴=，2AEG ABC S AE S AB ∆∆⎛⎫∴= ⎪⎝⎭，13AEG EBCGS S ∆=四边形，14AEG ABC S S ∆∆∴=，12AE AF AB AD ∴==，Rt ABC ∆，90ACD ACB ∴∠=∠=，CF ∴是中线，12CF AD ∴=,12CF AD ∴=．【总结】本题考查相似三角形的性质，直角三角形的性质，三角形一边的平行线等知识．【过关检测】一、单选题1．（2022秋·上海浦东新·九年级校考期中）两个相似三角形的对应角平分线的比为1:4，则它们的周长比为（ ） A ．1:4 B ．1:2C ．1:16D ．以上答案都不对【答案】A【分析】两个相似三角形的对应边的比，对应角平分线的比，对应中线的比，对应高线的比，周长的比都等于相似比．【详解】两个相似三角形的对应角平分线的比为1:4，∴两个相似三角形的相似比为1:4， ∴周长的比为1:4．ABCDEFG故选A ．【点睛】本题考查相似三角形的性质，解题的关键是熟记相似三角形的性质并灵活运用．在ABC 的边，ABC 的面积是A ．4B ．8【答案】A【分析】过点A 作AH BC ⊥于H ，交GF 于M ，如图，先利用三角形面积公式计算出8AH =，设正方形DEFG 的边长为x ，则,,8GF x MH x AM x ===−，再证明AGF ABC ∽，则根据相似三角形的性质得方程，然后解关于x 的方程即可．【详解】解：如图，过点A 作AH BC ⊥于H ，交GF 于M ，∵ABC 的面积是32，8BC =， ∴2132BC AH ⋅=，∴8AH =，设正方形DEFG 的边长为x ，则,,8GF x MH x AM x ===−， ∵GF BC ∥，∴AGF ABC ∽， ∴GF AMBC AH = ， 888x x −∴= ，解得∶4x =，即这个正方形的边长是4． 故选：A ．【点睛】本题考查了相似三角形的判定与性质及正方形的性质，添加合适的辅助线是解题的关键． 3．（2022秋·上海嘉定·九年级校考期中）已知两个相似三角形的相似比为49：，那么它们的面积比为（ ） A ．23： B ．818：C ．49：D ．1681：【答案】D【分析】根据相似三角形的面积比等于相似比的平方，即可得到答案．【详解】解：两个相似三角形的相似比为49：， ∴它们的面积比1618：故选D ．【点睛】本题考查了相似三角形的性质，熟练掌握相似三角形的面积比等于相似比的平方是解题关键． 九年级统考期中）已知ABC 的三边长分别为，DEF 的一边长，如果这两个三角形相似，那么DEF 的另两边长可能是（【答案】B【分析】根据三边对应成比例的三角形相似，即可求得．注意DEF 中为5cm 边长的对应边可能是6cm 或7.5cm 或9cm ，所以有三种情况．【详解】解：设DEF 的另两边为cm,cm x y ， 若DEF 中为5cm 边长的对应边为6cm ， 则：567.59x y==，解得：254x =，152y =； 若DEF 中为5cm 边长的对应边为7.5cm ，则：57.569x y ==，解得：4x =，6y =；若DEF 中为5cm 边长的对应边为9cm ， 则：5967.5x y ==，解得：103x =，256y =； 结合选项可得B 选项可选． 故选：B ．【点睛】此题考查了相似三角形的判定：三边对应成比例的三角形相似．解此题的关键要注意DEF 中为5cm 边长的对应边不确定，答案不唯一，要仔细分析，小心别漏解．九年级上海市华东模范中学校考期中）如图，在ABC 中，:ADEABCSS为（A ．3:5 【答案】C【分析】根据DE BC ∥可知ADEABC ，由:3:2AD DB =可知:3:5AD AB =,即相似比为3:5,再利用面积比是相似比的平方，即可判断求解． 【详解】解：∵DE BC ∥， ∴ADEABC ，∵:3:2AD DB =， ∴:3:5AD AB =，2239525ADE ABCSAD SAB ⎛⎫⎛⎫∴=== ⎪ ⎪⎝⎭⎝⎭， 故选：C ．【点睛】本题考查了相似三角形的判定与性质．用到的知识为：平行于三角形一边的直线与其他两边所截的三角形与原三角形相似，相似三角形对应边的比相等，都等于相似比，相似三角形面积的比等于相似比的平方．DEF 的最短边长为，那么DEF 的周长等于（126【答案】D【分析】由相似三角形的性质：周长的比等于相似比，求出相似比即可求得结果． 【详解】ABC DEF ∽，∴相似比为3193k ==，13ABC DEFC C∴=，33(356)42DEFABCCC ∴==⨯++=；故选：D ．【点睛】本题考查了相似三角形的性质，掌握相似三角形周长的比等于相似比是关键．是ABC 的重心，四边形与ABC 面积的比值是（【答案】B【分析】连接DE ，根据三角形中位线定理以及中线的性质可得1,2DE BC DE BC =∥，12ABDABCS S =，12BDEABDSS =，从而得到ADE ACB △△∽，进而得到221112,34AED ABCSD E E D S B G C G BD CE ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭==，继而得到13DEGBDESS =，14ADEABCSS =，可得1116212DEGABCABCSS S =⨯=，再由ADEDEGAEGD S SS=+四边形，即可．【详解】解：如图，连接DE ，∵点G 是ABC 的重心，∴点D ，E 分别为,AC AB 的中点，∴1,2DE BC DE BC =∥，12ABDABCS S =，12BDEABDSS =，∴ADE ACB △△∽， ∴12DG EG DE BG CG BC ===， ∴221112,34AED ABCSD E E D S B G C G BD CE ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭==， ∴13DEGBDES S =，14ADE ABCSS =，∴111326DEGABDABDS S S =⨯=， ∴1116212DEG ABCABCSS S =⨯=，∴1114123ADEDEGABCABCABCAEGD S SS S S S =+=+=四边形，即四边形AEGD 与ABC 面积的比值是13．故选：B【点睛】本题主要考查了三角形的重心，相似三角形的判定和性质，三角形中位线定理，熟练掌握三角形的重心，相似三角形的判定和性质，三角形中位线定理是解题的关键． 二、填空题8．（2022秋·上海长宁·九年级校考期中）已知ABC 与DEF 相似，且ABC 与DEF 的面积比为1:4，若DEF 的周长为16，那么ABC 的周长等于________．【答案】8【分析】根据相似三角形的面积的比等于相似比的平方先求出ABC 与DEF 的相似比，然后根据相似三角形的周长的比等于相似比解答即可．【详解】解：∵相似三角形ABC 与DEF 面积的比为1:4， ∴它们的相似比为1:2，∴ABC 与DEF 的周长比为1:2， ∵DEF 的周长为16， ∴ABC 的周长等于8， 故答案为：8．【点睛】本题主要考查了相似三角形面积的比等于相似比的平方，周长的比等于相似比的性质，熟记性质是解题的关键．9．（2022秋·上海奉贤·九年级校联考期中）已知ABC ∽111A B C △，顶点A 、B 、C 分别与1A 、1B 、1C 对应，AB ：113A B =：4，BE 、11B E 分别是它们的对应角平分线，则BE ：11B E =______． 【答案】3：4【分析】根据相似三角形对应角平分线的比都等于相似比解答即可． 【详解】解：ABC ∽111A B C △，BE ∴：11B E AB =：113A B =：4，故答案为：3：4．【点睛】本题考查的是相似三角形的性质，掌握相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比是解题的关键．10．（2022秋·上海浦东新·九年级校考期中）如图，DE BC ∥，:2:3AE EC =，则:OE OB =________．【答案】2:5【分析】根据:2:3AE EC =可求出:2:5AE AC =，再根据三角形相似的性质即可求解． 【详解】解：∵:2:3AE EC =，∴25AE AC =，∵DE BC ∥，∴25DE AE BC AC ==，且DEO CBO △∽△， ∴25OE DE OB CB ==， 故答案为：2:5．【点睛】本题主要考查比例的性质，相似三角形的性质，理解平行线的性质，相似三角形的性质是解题的关键．11．（2022秋·上海松江·九年级校考期中）已知ABC 和DEF 相似，对应边AB 与DE 之比为3:4，如果DEF 的周长为24，那么ABC 的周长是___________．【答案】18【分析】根据相似三角形的周长之比等于相似比得:3:4ABCDEFCC=，又因为DEF 的周长是24，再建立方程即可．【详解】解：∵ABC 和DEF 相似，对应边AB 与DE 之比为3:4， ∴:3:4ABCDEFCC=，∵DEF 的周长是24， ∴:243:4ABCC=∴ABC 的周长是18， 故答案为：18．【点睛】本题考查了相似三角形的性质，解题的关键是掌握相似三角形的周长之比等于相似比． 12．（2023·上海长宁·统考一模）如图，在ABC 中，90C ∠=︒，正方形EFGH 的边FG 在ABC 的边AB 上，顶点E 、H 分别在边AC 、BC 上，如果其面积为24，那么AF BG ⋅的值为______．【答案】24【分析】通过证明Rt Rt AFE HGB ∽，则AF BG EF HG ⨯=⨯，即可得到答案． 【详解】90C ∠=︒，正方形EFGH 的四个顶点在三角形的边上， 90A B ∴∠+∠=， 90B BHG ∠+∠=，Rt Rt AFE HGB ∴∽， =24AF BG EF HG ∴⨯=⨯．故答案为24．【点睛】本题主要涉及三角形相似的判定和相似三角形的性质应用，掌握相似三角形的判定和性质是解题的关键．，如果ABC 三边长分别是DEF 的两边长为【分析】根据相似三角形的性质列出比例式，代入数据即可求解．【详解】解：∵ABC DEF △△∽，∵ABC ，2，2，DEF 的两边长为1x∴21x ==，解得：x所以DEF ．．【点睛】本题考查了相似三角形的性质，求出相似比是解题关键．14．（2022秋·上海宝山·九年级统考期中）已知111ABC A B C :△△，顶点A 、B 、C 分别与1A 、1B 、1C 对应，11:3:5AB A B =，E 、1E 分别是边AC 、11AC 的中点，如果1BE =，那么11B E 的长为________． 【答案】53/213【分析】根据相似三角形对应中线的比等于相似比列比例式求解即可．【详解】解答：解：∵11111:35ABC A B C AB A B =∽，:，∴对应中线BE 、11B E 的比值为35:，∴11135B E =::， ∴1153B E =． 故答案为：53．【点睛】本题考查了相似三角形的性质，相似三角形对应中线的比等于相似比． 15．（2022秋·上海杨浦·九年级统考期中）如果两个相似三角形的面积比为3:4，那么它们对应高之比为__________．2 【分析】根据相似三角形的性质，两个相似三角形的面积比等于相似比的平方，因为两个相似三角形的面积比为3:42；再结合两个相似三角形对应高的比等于相似比即可得到答案． 【详解】解：两个相似三角形的面积比为3:4，∴2，∴2，2．【点睛】本题考查相似三角形的性质应用，熟练掌握形式三角形面积比等于相似比的平方，相似三角形对应高的比等于相似比是解决问题的关键． 16．（2023·上海·一模）如果ABC ∽DEF ，且ABC 的三边长分别为3、4、5， DEF 的最短边长为6，那么DEF 的周长等于________．【答案】24【分析】先设DEF 的周长等于c ，再根据相似三角形周长的比等于相似比即可求出c 的值．【详解】解；设DEF 的周长等于l ，∵ABC ∽DEF ，ABC 的三边长分别为3、4、5，DEF 的最短边长为6， ∴33546c ++=，解得24c = ．故答案为：24．【点睛】本题考查的是相似三角形的性质，即相似三角形周长的比等于相似比． 17．（2023·上海黄浦·统考一模）已知ABC 的三边长分别为2、3、4，DEF 与ABC 相似，且DEF 周长为54，那么DEF 的最短边的长是______．【答案】12 【分析】先计算出ABC 的周长，进而得出相似比为16∶，进而得出答案． 【详解】解：∵ABC 的三边长分别为2、3、4，∴ABC 的周长为：9∵DEF 与ABC 相似，且DEF 周长为54，∴ABC 与DEF 的周长比为95416=∶∶， ∴ABC 与DEF 的相似比为16∶， 设DEF 的最短边的长是x ，则：216x =∶∶，解得∶12x =．故答案为∶12．【点睛】本题主要考查相似三角形的性质，掌握相似三角形的周长比等于相似比是解题的关键．18．（2023·上海宝山·一模）已知一个三角形的三边之比为2:3:4，与它相似的另一个三角形ABC 的最小边长为4厘米，那么三角形ABC 的周长为 _____厘米．【答案】18【分析】相似三角形的对应边的比相等，因而与已知三角形相似的三角形的三边的比也是2:3:4，即可求得三角形的三边，从而求得周长．【详解】解：所求三角形的三边的比是2:3:4，设最短边是2x 厘米，则24=x ，解得2x =，因而另外两边的长是36x =厘米，48x =厘米．则三角形的周长是68418++=（厘米）．故答案为：18．【点睛】本题考查了相似三角形的性质，相似三角形对应边的比相等，由此得到所求三角形的三边的比也是2:3:4，是解题关键． 19．（2022·上海·九年级专题练习）两个相似三角形的面积之比是 9:25， 其中较大的三角形一边上的高是 5 厘米， 那 么另一个三角形对应边上的高为_________厘米．【答案】3【分析】把面积之比转换成相似比，在通过比例求出高 【详解】∵两个三角形面积比为9:25∴两个三角形相似比为3:5设：另一三角形对应边上的高为x∴355x =，解得x=3 故答案为：3【点睛】本题考查相似比和面积比的应用，掌握他们的区别是本题关键． 20．（2023·上海徐汇·统考一模）如图，在Rt ABC △中，90C ∠=︒，2AC =，1BC =，正方形DEFG 内接于ABC ，点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长是______．【答案】【分析】过点C 作C M A B ⊥于点M ，交GF 于点N ，首先由勾股定理得出AB 的长，由面积法即可求出CM 的长，可证得CGF CAB ∽，再根据相似三角形的性质，即可得出答案．【详解】解：如图：过点C 作C M A B ⊥于点M ，交GF 于点N ，Rt ABC △中，90C ∠=︒，2AC =，1BC =，AB ∴，1122ABC S AC BC AB CM =⋅=⋅△，∴AC BC CM AB ⋅∴===， ∵正方形DEFG 内接于ABC ，GF EF MN ∴==，GF AB ∥，CGF CAB ∴△∽△，CN GF CM AB ∴=，EF −=，解得：EF =，故答案为：．【点睛】本题考查的是相似三角形的判定和性质、正方形的性质、勾股定理等知识；正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键． 21．（2023·上海虹口·校联考二模）如图，在ABC 中，点D 、E 分别在边BC AC 、上，ABE C ∠=∠，DE AB ∥，如果6AB =，9AC =，那么:BDE CDE S S △△的值是______．【答案】4:5【分析】根据已知证明ABE ACB ∽，得出4AE =，进而得出5EC =，根据DE AB ∥，根据平行线分线段成比例，得出45AE BD EC DC ==，即可求解． 【详解】解：∵BAE CAB ∠=∠，ABE C ∠=∠，∴ABE ACB ∽，∵6AB =，9AC =，∴AB AE AC AB =∴24AB AE AC ==，∴945EC AC AE =−=−=，∵DE AB ∥，∴45AE BD EC DC == ∴:BDE CDE S S △△=::4:5BD DC AE EC ==，故答案为：4:5．【点睛】本题考查了相似三角形的性质与判定，平行线分线段成比例，熟练掌握相似三角形的性质与判定是解题的关键．22．（2023·上海·一模）如果梯形的一条对角线把梯形分成的两个三角形相似，那么我们称该梯形为“优美梯形”．如果一个直角梯形是“优美梯形”，它的上底等于2，下底等于4，那么它的周长为______．【答案】8+8【分析】根据 “优美梯形”的定义，得到ABD BDC ∽△△，从而得到90CBD BAD ∠=∠=︒，AD AB BD BC BD CD ==，推出2BD AB CD =⋅，算出BD =再根据勾股定理，得到AD 、BC 的长，即可得到该直角梯形的周长．【详解】解：根据题意，作图如下，ABCD 为直角梯形，90BAD ADC ∴∠=∠=︒，90ABD ADB ∴∠+∠=︒，90ADB BDC ∠+∠=︒，ABD BDC ∴∠=∠，直角梯形ABCD 是“优美梯形”，ABD BDC ∴∽，90CBD BAD ∴∠=∠=︒，AD AB BD BC BD CD ==，2BD AB CD ∴=⋅，2AB =，4CD =，BD ∴，在Rt ABD 中，2AD ，在Rt BCD △中，BC =∴该梯形的周长2428AB BC CD DA =+++=++=+故答案为：8+【点睛】本题考查了直角梯形的性质，相似三角形的性质，勾股定理，熟练掌握相似三角形的性质是解题关键． 23．（2022秋·上海奉贤·九年级校联考期中）如图，在梯形ABCD 中，AD BC ∥，AC 与BD 相交于点O ，如果2ABC ACD S S =，那么COD S △：ABC S =______．【答案】1：3/13【分析】首先根据2ABC ACD S S =，可得AD ：1BC =：2；然后根据AOD ∴∽COB ，可得AO ：OC OD =：OB AD =：1BC =：2，进而可得AOD S：1BOC S =：4，AOD S ：1AOB S =：2，AOD S ：1OCD S =△：2，设AOD S k =，分别表达OCD S 和ABC S 进而可得结论．【详解】解：在梯形ABCD 中，//AD BC ，2ABC ACD S S =，AD ∴：1BC =：2；//AD BC ，AOD ∴∽COB ，AO ∴：OC OD =：OB AD =：1BC =：2，AOD S∴：1BOC S =：4，AOD S ：1AOB S =：2，AOD S ：1OCD S =△：2， 设AOD S k=，则4BOC S k =，2AOB OCD S S k ==， 6ABC AOB BOCS S S k ∴=+=， COD S ∴：2ABC S k =：61k =：3．故答案为：1：3．【点睛】此题主要考查了相似三角形的判定与性质的应用，以及梯形的特征和应用，要熟练掌握．三、解答题24．（上海·九年级校考阶段练习）如图，已知梯形ABCD ，AB ∥DC ，△AOB 的面积等于9，△AOD 的面积等于6，AB ＝7，求CD 的长．【答案】143【详解】试题分析：由题意易得△COD ∽△AOB ，由此可得：CD DO AB BO =；由△AOB 的面积等于9，△AOD 的面积等于6，可得：23DO BO =，再结合AB=7即可求得CD 的长.试题解析：∵AB ∥DC ，∴△COD ∽△AOB ， ∴CD DO AB BO =，∵△AOB 的面积等于9，△AOD 的面积等于6， ∴23DO BO =， ∴23CD DO AB BO ==， 又∵AB ＝7， ∴273CD =， ∴CD ＝143.【答案】20平方厘米【分析】根据两个相似三角形的面积比等于对应边的比的平方，结合面积和即可求解．【详解】解：设两个三角形的面积分别为x ，y ，则有22365x y x y ⎧⎛⎫=⎪ ⎪⎨⎝⎭⎪+=⎩，解得2045x y =⎧⎨=⎩；答：较小三角形面积为20平方厘米．【点睛】本题考查的是相似三角形的性质，解题的关键是掌握相似三角形的面积比等于对应边的比的平方．26．（2020秋·上海宝山·九年级统考阶段练习）如图，正方形DEFG 的边EF 在ABC ∆的边上，顶点D 、G 分别在边AB 、AC 上，已知ABC ∆的边15BC =，高10AH =，求：正方形DEFG 的边长和面积．【答案】6，36【分析】由正方形的性质可得DG //BC ，不难证明ADG △∽ABC ，即DG AM BC AH =，设正方形的边长为x ，分别表示出对应边的长度并代入DG AM BC AH =求解，即可得出正方形的边长，即可得出正方形的面积． 【详解】设正方形的边长为x ，正方形DEFH ，AH ⊥BC ，∴DG=GF=MH=x ，DG //BC ，∴ADG=B ∠∠，AM=10－x ，在ADG △与ABC 中，ADG=BAC BAC B ∠=∠⎧⎨∠∠⎩，∴ADG △∽ABC ，∴DG AM BC AH =，∴101510x x −=， 解得：x=6，S=6×6=36．答：正方形的边长为6，面积为36．【点睛】本题主要考查正方形的性质以及相似三角形的判定与性质，设正方形的边长为x ，根据相似比等于高之比列方程求解是解题关键．27．（上海·九年级阶段练习）如图，△ABC是一块锐角三角形的材料，边BC＝120mm，高AD＝80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少mm．【答案】48mm【分析】设正方形EF=EG=ID=x，根据正方形的性质，得到EF∥BC，△AEF∽△ABC，列出比例式EF AIBC AD=，代入计算即可．【详解】∵四边形EFHG是正方形，AD是高，∴ EF∥BC，四边形EGDI是矩形，∴ EG=ID，设正方形EF=EG=ID=x，∴△AEF∽△ABC，∴EF AI BC AD=，∵ BC＝120mm，高AD＝80mm，∴80 12080x x−=，解得x=48，故正方形的边长为48mm．【点睛】本题考查了正方形的性质，三角形相似的判定和性质，熟练掌握三角形相似的性质是解题的关键．。
(完整)相似三角形常见题型解法归纳,推荐文档
A 字形，A’形，8字形，蝴蝶形，双垂直,旋转形双垂直结论:射影定理：角边是这条直角边在斜边上的射影和斜边的比例中项⑴△ACD∽△CDB→AD:CD=CD:BD→CD 2=AD•BD ⑵△ACD∽△ABC→AC:AB=AD:AC →AC 2=AD•AB ⑶△CDB∽△ABC→BC:AC=BD:BC →BC 2=BD•AB结论：⑵÷⑶得AC 2:BC 2=AD:BD结论：面积法得AB•CD=AC•BC→比例式 证明等积式(比例式)策略1、直接法：找同一三角形两条边变化：等号同侧两边同一三角形 三点定形法2、间接法： ⑴3种代换 ①等线段代换； ②等比代换； ③等积代换； ⑵创造条件 ①添加平行线——创造“A”字型、“8”字型 ②先证其它三角形相似——创造边、角条件相似判定条件：两边成比夹角等、两角对应三边比 相似终极策略：遇等积，化比例，同侧三点找相似； 四共线，无等边，射影平行用等比； 四共线，有等边，必有一条可转换； 两共线，上下比，过端平行条件边。
彼相似，我角等，两边成比边代换。
（3）等比代换：若是四条线段，欲证，可先证得（是两条线段）然d c b a ,,,dc b a =fe b a =fe ,后证，这里把叫做中间比。
dc f e =fe ①∠ABC =∠ADE ．求证：AB ·AE =AC ·AD②△ABC 中，AB=AC ，△DEF 是等边三角形,求证：BD•CN=BM•CE ．③等边三角形ABC 中，P 为BC 上任一点，AP 的垂直平分线交AB 、AC 于M 、N 两点。
求证：BP •PC=BM•CN☞有射影，或平行，等比传递我看行斜边上面作高线，比例中项一大片①在Rt△ABC 中，∠BAC=90°，AD⊥BC 于D ，E 为AC 的中点，求证：AB•AF=AC•DF②ABCD③梯形ABCD 中，AD//BC ，作BE//CD,求证：OC 2=OA.OE☞四共线，看条件，其中一条可转换；①Rt △ABC 中四边形DEFG 为正方形。
相似三角形(8大题型)(48道压轴题专练)(原卷版)—2024-2025学年九年级数学上册单元速记巧
相似三角形（8大题型）（48道压轴题专练） 压轴题型一 相似形压轴题型1．（20-21九年级上·重庆渝中·期末）如图，△ABC 三个顶点的坐标分别是A （－2，2），B （－4，1），C （－1，－1）．以点C 为位似中心，在x 轴下方作△ABC 的位似图形△A'B'C ．并把△ABC 的边长放大为原来的2倍，那么点A'的坐标为( )A ．（1，－6）B ．（1，－7）C ．（2，－6）D ．（2，－7）2．（23-24八年级下·山东淄博·(2)ABCD AD AB AD <<纸片，以它的一边为边长剪去一个菱形，在余下的平行四边形中，再以它的一边为边长剪去一个菱形．若剪去两个菱形后余下的平行四边形与原平行四边形ABCD 相似，则平行四边形ABCD 的相邻两边AD 与AB 的比值是 ．3．（2024·湖北武汉·一模）如图是由小正方形组成的网格，四边形ABCD的顶点都在格点上，仅用无刻度的直尺在所给定的网格中按要求完成下列画图，画图过程用虚线表示，画图结果用实线表示．(1)在图1中，先以点A为位似中心，将四边形ABCD缩小为原来的12，画出缩小后的四边形111AB C D，再在AB上画点E，使得DE平分四边形ABCD的周长；(2)在图2中，先在AB上画点F，使得CF BC=，再分别在AD，AB上画点M，N，使得四边形BCMN 是平行四边形．4．（23-24九年级上·江苏南京·阶段练习）形状相同（即长与宽之比相等）的矩形是相似矩形，已知一个矩形长为()1a a³，宽为1．一分为二（1）如图1，将矩形分割为一个正方形（阴影部分）和小矩形，小矩形恰与原矩形相似，则a的值为______．（2）如图2，将矩形分割为两个矩形，使每个小矩形均与原矩形相似，则a的值为______．一分为多（3）有同学说“无论a为何值，该矩形总可以分割为几个小矩形，这几个小矩形都与原矩形相似”，你同意这个说法吗？若同意，在图3中画出一种可行的分割方案；若不同意，举出反例．一分为三（4）将矩形分割为三个矩形，使每个小矩形均与原矩形相似．画出所有可能的分割方案的示意图，并在每个示意图下方直接写出对应的a 的值．5．（20-21八年级下·山东淄博·期末）如图，四边形ABCD ∽四边形A B C D ¢¢¢¢，且62A Ð=°，75B Ð=°，140D Т=°，9AD =，11A B ¢¢=，6A D ¢¢=，8B C ¢¢=．(1)请直接写出：C Ð= 度；(2)求边AB 和BC 的长．6．（23-24九年级上·广西南宁·阶段练习）如图，在平面直角坐标系中，ABC V 的三个顶点坐标分别为()1,1A ，()3,2B ，()2,3C （每个方格的边长均为1个单位长度），请按下列要求画图：(1)111A B C △与ABC V 关于原点O 成中心对称，画出111A B C △并写出点1A 的坐标；(2)以原点O 为位似中心，相似比为2，在第一象限内将ABC V 放大，画出放大后的222A B C △并写出点2B 的坐标；(3)根据信息回答问题：已知ABC V 的面积为32，AB ，请直接写出222A B C △的面积和22A B 边上的高的值．压轴题型二 比例线段压轴题型1．（2020古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底0.618≈，称为黄金分割比例），如图，著名的“断臂维纳斯”便是如此．此外，．若某人满足上述两个黄金分割比例，且腿长为105cm ，头顶至脖子下端的长度为26cm ，则其身高可能是（ ）A ．165cmB ．175cmC ．185cmD ．190cm2．（2024·四川乐山·一模）古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将线段MN 分为两线段MG ，GN ，使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项，即满足MG GN MN MG ==这个数称为“黄金分割”数，把点G 称为线段MN 的“黄金分割”点．如图，在ABC V 中，已知3AB AC ==，4BC =，若D ，E 是边BC 的两个“黄金分割”点，则ADE V 的面积为 ．3．（23-24八年级下·贵州六盘水·期末）已知a ，b ，c ，d ，e ，f 六个数，如果()0a c e k b d f b d f ===++¹，那么a c e k b d f++=++．理由如下：∵()0a c e k b d f b d f===++¹∴a bk =，c dk =，e fk =（第一步）∴()k b d f a c e bk dk fk k b d f b d f b d f++++++===++++++（第二步）(1)解题过程中第一步应用了______的基本性质；在第二步解题过程中，()k b d f k b d f ++=++应用了______的基本性质；(2)应用此解题过程中的思路和方法解决问题：①如果22567a b c ===，则218a b c ++=______；②已知0345x y z ==¹，求23x y z x y z -++-的值．4．（23-24九年级上··的矩形叫黄金矩形．如图①，已知黄金矩形ABCD 的宽1AB =．(1)黄金矩形ABCD 的长BC = ；(2)如图②，将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ，得到新的矩形DCEF ，猜想矩形DCEF 是否为黄金矩形，并证明你的结论；(3)在图②中，连接AE ，求点D 到线段AE 的距离．5．（22-23九年级上·浙江·周测）若实数a b c ，，满足a b c b c a a c b c a b +-+-+-==，求()()()a b b c a c abc+×+×+的值．6．（23-24九年级下·山东淄博·期末）已知a ，b ，c ，d 为四个不为0的数．(1)如果3a b =，求a b b +与a b a b -+的值；(2)如果(),a c a b c d b d =¹¹，求证a c b a d c =--；(3)如果a c a b d b +=+，求证a c b d=．压轴题型三 相似三角形的判定压轴题型1．（21-22九年级上·陕西咸阳·期中）如图，在矩形ABCD 中，E 是AD 边的中点，BE ^F ，连接DF ，分析下列四个结论，①AEF CAB △∽△，②CF 2AF =；③DF DC =；④CD AC =．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个2．（2024·广东深圳·二模）如图，在等腰直角ABC V 中，4AB BC ==，D 为BC 上一点，E 为BC 延长线上一点，且45DAE =°∠，2AE AD =，则BD = ．3．（2024·广东梅州·模拟预测）（1）如图1，在矩形ABCD 中，点C ，D 分别在边DC ，BC 上，AB AB ^，垂足为点G ．求证：ADE DCF ∽V V ．【问题解决】（2）如图2，在正方形ABCD 中，点E ，F 分别在边DC ，BC 上，AE DF =，延长BC 到点H ，使CH DE =，连接DH ．求证：ADF H Ð=Ð．【类比迁移】（3）如图3，在菱形ABCD 中，E F 分别在边DC ，BC 上，10AE DF ==，7DE =，60AED Ð=°，求CF 的长．4．（2024·山西晋中·二模）综合与实践问题情境：数学活动课上，老师要求同学们以正方形为背景探索几何图形运动变化中的数学结论．如图1，正方形ABCD 中，4AB =，点E ，F 分别是边AB ，AD 的中点，连接EF ，点G 是线段EF 上的一个动点，连接AG ，将线段AG 绕点A 逆时针方向旋转90°，得到AH ，连接HD ，GB ．猜想证明：（1）针对老师给出的问题背景，“智慧小组”发现GB HD =，请你证明这一结论；操作探究：（2）“善思小组”提出问题：如图2，当点G 为线段EF 的中点时，连接FH ，试判断四边形AGFH 的形状，并说明理由；深入探究：（3）“创新小组”BG 与直线DH 交于点M ，当AHD V 为直角三角形时，请直接写出四边形AGMH 的面积．5．（2024·安徽蚌埠·一模）如图1，在四边形ABCD 中，120ABC Ð=°，60ADC Ð=°，对角线AC ，BD 相交于点O ，且AC AD =，BD 平分ABC Ð．(1)求证：DB AB CB =+；(2)如图2，过点D 作DE AB ∥，使DE BC =，连接AE ，取AE 中点 F ，连接DF ，求证：22AC DF OD =×．6．（23-24九年级上·湖南常德·期中）（1）如图1，在四边形ABCD 中，90BAD BCD Ð=Ð=°，连接AC BD ，，过点A 作AE AC ^交CB 的延长线于点E ，求证：E ACD Ð=Ð．（2）如图2，在四边形ABCD 中，AB AD =，（1）中的其它条件不变，点M ，N 分别是BD EC ，的中点，连接AN AM ，，MN ．①求证：AE AC =﹔②求证：N ABE AM ∽△△．压轴题型四 相似三角形的性质压轴题型1．（22-23九年级上·上海长宁·期中）已知点D 在ABC V 的边BC 上，联结AD ，如果ABD △与ACD V 相似，那么下列四个说法：①BAD C Ð=Ð；②AD BC ^；③2AD BD CD =×；④22AB BD AC CD =．一定成立的是（ ）．A ．②④B ．①③C ．①②③D ．②③④2．（2024·上海浦东新·三模）如图，在ABC V 中，3AC BC ==，90C Ð=°，点D 在边BC 上（不与点B ，点C 重合），连接AD ，点E 在边AB 上，EDB ADC Ð=Ð．已知点H 在射线AC 上，连接EH 交线段AD 于点G ，当1CH =，且AEH BED Ð=Ð时，则BE AB = ．3．（23-24八年级下·山东威海·期末）如图1，矩形ABCD ，点E ，点F 分别为AD ，BC 上的点，将矩形沿EF 折叠，使点B 的对应点B ¢落在CD 上，连接BB ¢．(1)如图2，当点B ¢与点D 重合时，连接BE ，试判断四边形BEB F ¢的形状，并说明理由；(2)若6AB =，8BC =，求折痕EF 的最大值．4．（23-24八年级下·山东东营·期末）综合与探究(1)如图1，在正方形ABCD 中，点E ，F 分别在边BC CD ，上，且AE BF ^，则线段AE 与BF 的之间的数量关系为_____________；(2)【类比探究】如图2，在矩形ABCD 中，35AB AD ==，，点E ，F 分别在边BC ，CD 上，且AE BF ^，请写出线段AE 与BF 的数量关系，并证明你的结论．(3)【拓展延伸】如图3，在Rt ABC V 中，9046ABC AB BC Ð=°==，，，D 为BC 上一点，且2BD =，连接AD ，过点B 作BE AD ^于点F ，交AC 于点E ，求BE 的长．5．（23-24九年级下·广西南宁·阶段练习）已知等边ABC V ，以AC 为斜边向外作Rt ACD △，定义Rt ACD △为等边ABC V 的“关联直角三角形”，连接BD 交AC 于点E ，下面我们来研究与DE BE的值有关的问题．(1)如图①，当“关联直角三角形”是等腰直角三角形时，DE BE的值为______；(2)如图②，当“关联直角三角形”是含30°的直角三角形时，求DE BE的值；(3)如图③，当“关联直角三角形”是一般的直角三角形时，若16,3DE AB BE ==，求BD 的值．6．（2024·安徽·中考真题）如图1，ABCD Y 的对角线AC 与BD 交于点O ，点M ，N 分别在边AD ，BC 上，且AM CN =．点E ，F 分别是BD 与AN ，CM 的交点．(1)求证：OE OF =；(2)连接BM 交AC 于点H ，连接HE ，HF ．（ⅰ）如图2，若HE AB ∥，求证：HF AD ∥；（ⅱ）如图3，若ABCD Y 为菱形，且2MD AM =，60EHF Ð=°，求AC BD 的值．压轴题型五 相似三角形的应用压轴题型1．（2024·浙江温州·三模）图1是《九章算术》中记载的“测井深”示意图，译文指出：“如图2，今有井直径CD 为5尺，不知其深AD ．立5尺长的木CE 于井上，从木的末梢E 点观察井水水岸A 处，测得“入径CF ”为4寸，问井深AD 是多少？（其中1尺10=寸）”根据译文信息，则井深AD 为（ ）A ．500寸B ．525寸C ．550寸D ．575寸2．（2022·浙江金华·一模）将一本高为17cm （即17cm EF =）的词典放入高（AB ）为16cm 的收纳盒中（如图1）．恰好能盖上盒盖时，测得底部F 离收纳盒最左端B 处8cm ，若此时将词典无滑动向右倒，书角H 的对应点H ¢恰为CD 中点．（1）收纳盒的长BC = ；（2）现将若干本同样的词典放入此有盖的收纳盒中，如图2放置，则最多有本书可与边BC 有公共点．3．（2024·江苏南京·一模）在光学中，由实际光线会聚成的像，称为实像，而光线能会聚的是因为折射．图中，凸透镜EF 的焦距为f ，主光轴l EF ^，A ，B ，C ，D 都在l 上，其中O 是光心，2OB OD f ==，蜡烛PQ l ^（蜡烛可移动，且OQ f >），光线PG l ∥，其折射光线GC 与另一条经过光心的光线PP ¢相交于点P ¢（P Q l ¢¢^）即为蜡烛在光屏上所成的实像．图中所有点都在同一平面内．记物高()PQ 为h ，像高()P Q ¢¢为h ¢，物距()OQ ，像距()OQ ¢为v ．(1)若10cm f =，10cm h =，15cm u =，=v cm ．(2)求证111u v f+=．(3)当f 一定时，画出v 与u 之间的函数图象()u f >，并结合图象描述v 是怎么随着u 的变化而变化的？4．（23-24九年级上·河北邢台·1，小红家的阳台上放置了一个晒衣架，图2是晒衣架的侧面示意图，立杆AB 、CD 相交于点O ，B 、D 两点在地面上，经测量得到136cm AB CD ==，51cm OA OC ==，34cm OE OF ==，现将晒衣架完全稳固张开，扣链EF 成一条线段．发现：连接AC ．则AC 与EF 有何位置关系?并说明理由；探究：若32cm EF =，求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时，连衣裙才不会拖在地面上?5．（22-23九年级上·浙江·单元测试）如图，Rt ABC V 为一块铁板余料，90B Ð=°，6cm BC =，8cm AB =，要把它加工成正方形小铁板，有如图所示的两种加工方案，请你分别计算这两种加工方案的正方形的边长．6．（2022九年级·全国·专题练习）阅读理解：如图1，AD 是△ABC 的高，点E 、F 分别在AB 和AC 边上，且EF //BC ，可以得到以下结论：AH EF AD BC=．拓展应用：(1)如图2，在△ABC 中，BC ＝3，BC 边上的高为4，在△ABC 内放一个正方形EFGM ，使其一边GM 在BC 上，点E 、F 分别在AB 、AC 上，则正方形EFGM 的边长是多少？(2)某葡萄酒庄欲在展厅的一面墙上，布置一个腰长为100cm ，底边长为160cm 的等腰三角形展台．现需将展台用隔板沿平行于底边，每间隔10cm 分隔出一排，再将每一排尽可能多的分隔成若干个无盖正方体格子，要求每个正方体格子内放置一瓶葡萄酒．平面设计图如图3所示，将底边BC 的长度看作是0排隔板的长度．①在分隔的过程中发现，当正方体间的隔板厚度忽略不计时，每排的隔板长度（单位：厘米）随着排数（单位：排）的变化而变化．请完成下表：排数/排0123…隔板长度/厘米160__________________…若用n 表示排数，y 表示每排的隔板长度，试求出y 与n 的关系式；②在①的条件下，请直接写出该展台最多可以摆放多少瓶葡萄酒？压轴题型六 重心的性质压轴题型1．（23-24九年级上·浙江宁波·期末）如图，点G 是ABC V 的重心，过点G 作MN BC ∥分别交AB AC ，于点M ，N ，过点N 作ND AB ∥交BC 于点D ，则四边形BDNM 与ABC V 的面积之比是（ ）A ．1:2B ．2:3C ．4:9D ．7:92．（2023·上海·一模）在Rt ABC △中，9030B BAC BC Ð=°Ð=°=，，1，以AC 为边在ABC V 外作等边ACD V ，设点E 、F 分别是ABC V 和ACD V 的重心，则两重心E 与F 之间的距离是 ．3．（2024·江苏盐城·中考真题）如图1，E 、F 、G 、H 分别是平行四边形ABCD 各边的中点，连接AF CE 、交于点M ，连接AG 、CH 交于点N ，将四边形AMCN 称为平行四边形ABCD 的“中顶点四边形”．(1)求证：中顶点四边形AMCN 为平行四边形；(2)①如图2，连接AC BD 、交于点O ，可得M 、N 两点都在BD 上，当平行四边形ABCD 满足________时，中顶点四边形AMCN 是菱形；②如图3，已知矩形AMCN 为某平行四边形的中顶点四边形，请用无刻度的直尺和圆规作出该平行四边形．（保留作图痕迹，不写作法）4．（23-24七年级下·江苏扬州·阶段练习）作图．(1)直尺作图：如图1，已知D 、E 分别为AB 、AC 中点，过点A 作AF 平分ABC V 面积；(2)直尺作图：如图2，已知AD BC ∥，在四边形ABCD 中作一点O ，使AOB COD S S =△△；(3)尺规作图：如图3，已知D 为AC 中点，点M 在BC ，在AC 上作点N 使MN 平分ABC V 面积．5．（2024·辽宁丹东·二模）阅读与思考：三角形的重心定义：三角形三条中线相交于一点，这个交点叫做三角形的重心．三角形重心的一个重要性质：重心与一边中点的连线的长是对应中线长的13．下面是小明证明性质的过程．如图，在ABC V 中，D 、E 分别是边BC 、AC 的中点，AD 、BE 相交于点G ，求证：13GE GD BE AD ==证明：连接ED ，∵D ，E 是边BC ，AC 的中点，∴DE AB ∥，12DE AB =（依据1）∴ABG DEGV V ∽∴12GE GD DE GB GA AB ===（依据2）∴13GE GD BE AD ==(1)任务一，在小明的证明过程中，依据1和依据2的内容分别是：依据1：______________________依据2：______________________(2)应用①如图，在ABC V 中，点G 是ABC V 中的重心，连接AG 并延长交BC 与点E ，若 3.5GE =，求AG 长．②在ABC V 中，中线AD 、BE 相交于点O ，若ABC V 的面积等于30，求BOD V 的面积．6．（2024·河南周口·三模）（1）古往今来，人们在生产和生活中对三角形的应用层出不穷，三角形也是我们平时研究的重点，如图1，已知ABC V 是等边三角形． P 是ABC V 的重心，连接BP CP ，并延长分别交边AC AB ，于点E ，D ．试判断：①BPD Ð的度数为 ；②线段PB PD PE ，，之间的数量关系：PB PD PE +；（填写“>”“<”或“=”）（2）如图2，若在等边ABC V 中，点E 是射线AC 上一动点（其中点E 不与点A 重合，且12CE AC <），连接BE ，作边BA 关于直线 BE 的对称线段 BD ，直线CD ，BE 相交于点 P ，试探究线段PB PC PD ，，的数量关系，并说明理由．压轴题型七 平面向量的线性运算压轴题型1．（23-24九年级上·上海·期中）下列判断不正确的是（ ）A ．()222a b a b +=+r r r r ；B ．如果向量a r 与b r 均为单位向量，那么a b =r r 或a b =-r r ；C ．如果a b =r r ，那么a b =r r ；D ．对于非零向量b r ，如果()0a k b k =×¹r r ，那么a b r r P ．2．（2024·上海普陀·二模）如图，梯形ABCD 中，AD BC ∥，过点A 作AE DC ∥分别交BD 、BC 于点F 、E ，23BE BC =，设AD a =uuu r r ，AB b =uuu r r ，那么向量FE uuu r 用向量a r 、b r 表示为 ．3．（23-24八年级下·上海崇明·期末）如图，点E 在平行四边形ABCD 的对角线BD 的延长线上．(1)填空：BA AB +uuu r uuu r ＝ ，BA AE ED DC +++uuu r uuu r uuu r uuu r ＝ ；(2)图中与AB uuu r 相等的向量是 ，与AD uuu r 相反的向量是 ；(3)求作：DC DE +uuu r uuu r （不写作法，保留作图痕迹，写出结论）．4．（23-24八年级下·上海·期末）如图，在四边形ABCD 中，AD BC ∥，点O 是对角线AC 的中点，DO 的延长线与BC 相交于点E ，设AB a uuu r r =，AD b =uuu r r ，BE c =uuu r r ．(1)试用向量a r 、b r 、c r 表示向量：ED =uuu r ______；(2)写出图中所有与AD uuu r 互为相反向量的向量：______；(3)求作：AD OC +uuu r uuu r．（画出所求向量，并直接写出结论）5．（23-24八年级下·上海闵行·期末）如图，已知梯形ABCD 中，AB DC P ，点E 在AB 上，ED BC ∥．(1)填空：BE ED DC CB +++=uuu r uuu r uuu r uuu r ，(2)填空：BA AD DC EA ++-=uuu r uuu r uuu r uuu r ；(3)在图中直接作出AE ED AB +-uuu r uuu r uuu r ．（不写作法，写结论）6．（2022八年级下·上海·专题练习）如图，已知点M 是△ABC 边BC 上一点，设AB uuu r ＝a r ，AC uuu r ＝b r ．(1)当BM MC＝2时，AM uuuu r ＝______；（用a r 与b r 表示）(2)当AM uuuu r ＝4377a b +r r 时，BM MC ＝______；(3)在原图上作出AM uuuu r 在AB uuu r 、AC uuu r 上的分向量．压轴题型八 相似三角形的动点问题1．（2020·山西·一模）如图，在ABC V 中，8AB AC ==，6BC =，点P 从点B 出发以1个单位长度/秒的速度向点A 运动，同时点Q 从点C 出发以2个单位长度/秒的速度向点B 运动，其中一点到达另一点即停．当以B ，P ，Q 为顶点的三角形与ABC V 相似时，运动时间为（ ）A ．2411秒B ．95秒C ．2411秒或95秒D ．以上均不对2．（2023八年级上·江苏·专题练习）如图，在ABC V 中，90C Ð=°，3AC =，4BC =，动点P 从点B 出发以每秒1个单位长度的速度沿B A ®匀速运动；同时点Q 从点A 出发同样的速度沿A C B ®®匀速运动．当点P 到达点A 时，P 、Q 同时停止运动，设运动时间为t 秒，当t 为 时，以B 、P 、Q 为顶点的三角形是等腰三角形．3．（2024·吉林长春·三模）如图，在Rt ABC △中，90ABC Ð=°，8AB =，6BC =，点D 为AC 中点，动点P 从点A 出发，沿边AB 以每秒5个单位长度的速度向终点B 运动，连结DP ，将线段DP 绕点D 逆时针旋转90°得线段DE ，连结PE ．设点P 运动的时间为t 秒．(1)用含t 的代数式表示点P 到AC 的距离为________；(2)当点E 落在ABC V 内部（不包括边界）时，求t 的取值范围；(3)当PE 与ABC V 的一边平行时，求线段PE 的长度；(4)当经过点E 与ABC V 的一个顶点的直线平分ABC V 面积时，直接写出t 的值．4．（2024·江苏苏州·二模）如图，矩形ABCD 中，4AB ＝厘米，3BC ＝厘米，点E 从A 出发沿AB BC -匀速运动，速度为1厘米/秒；同时，点F 从C 出发沿对角线CA 向A 匀速运动，速度为1厘米/秒，连接DE DF EF 、、，设运动时间为t 秒．请解答以下问题：(1)当0 2.5t ＜＜时①t 为何值时，EF AD ∥；②设DEF V 的面积为y ，求y 关于t 的函数；5．（2023·吉林松原·模拟预测）已知ABC V 中，90C Ð=°，3cm AC =，4cm CD =，BD AD =．点F 从点A 出发，沿AC CD -运动，速度为1cm/s ，同时点E 从点B 出发，沿BD DA -运动，运动速度为1cm/s ，一个点到达终点，另一点也停止运动．设AEF △ 的面积为S 2cm ，点E ，F 运动时间为t s ．(1)求BD 的长；(2)用含t 的代数式表示DE ；(3)求S 与t 的函数关系式，并写出t 的取值范围．6．（23-24九年级下·河北邯郸·阶段练习）如图1和2，在矩形ABCD 中，6,8AB BC ==，点K 在CD 边上．且73CK =．点M N ，分别在,AB BC 边上，且2AM CN ==．点P 从点M 出发沿折线MB BN -匀速运动，点E 在CD 边上随P 移动，且始终保持^PE AP ；点Q 从点D 出发沿DC 匀速运动，点P Q ，同时出发，点Q 的速度是点P 的一半，点P 到达点N 时停止，点Q 随之停止．设点P 移动的路程为x ．(1)当点Q 与点K 重合时，通过计算确定点P 的位置；(2)若点P 在BN 上，当BP CE =时，如图2，求x 的值；(3)在点P 沿折线MB BN -运动过程中，求点Q ，E 的距离（用含x 的式子表示）；(4)已知点P 从点M 到点B 再到点N 共用时20秒，请直接写出点K 在线段QE 上（包含端点）的总时长．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相似三角形的常见题型
【知识要点】
1.如何选择相似三角行判定定理：
①已知一个角对应相等的，常用（两角型或夹角与一组对应边成比例）
②已知一组对边成比例的，常用（夹角与一组对应边成比例）
③只知道边的关系的，常用（三边对应成比例）
【学堂练习】
1.如图，□中，直线分别交、的延长线于P、S交、、于Q、E、R，
图中相似三角形的对数（不含全等三角形）共有
对。
2.如图，□中，交延长线于E交于F，∶＝3∶ 2，则∶。
A R
S
D
C
Q
E
B
【经典例题】
例1、如图，在△中，∥，∥.
（1）求证：：：
（2）若4，5，求的长.
例2、如图，∠1＝∠2，＝12，＝15，＝20，＝25。
证明：△∽△。
例3
E是边延长线上一点，交于F，交于G，
求证：（1）2·。
（2）
AE
AB
CB
CF。
A
C
D E
题
B
C
D
E
例4、 如图，△中，D 是边上的中点，且＝，⊥，与相交于点E ，
与相交于点F 。
（1）求证：△∽△； （2）若S BC FCD
∆==510，，求的长。
例5．如图, △是等边三角形,点分别在上,且与相交于点F.
(1) △与△相似吗?说说你的理由. (2)2
·吗?请说明理由.
例6．如图，⊥，⊥，、相交于点C，⊥，垂足为F。
（1）求证：111
AD BE CF
+=。
【随堂练习】D
A F B
E
C
1．如图所示，∥，
32=DB AD ，则BC
DE
= 。
2．如图所示，∥，∥，1.8， 1.2，1，则 。
3．如图所示，∥，∥，则下列比例式正确的是（ ）。
A ．
BC
DE
BD AD = B ．
FC
BF
EC AE = C ．
BC
DE
AC DF =
D ．BC
BF AC DF =
4. 如图，在正三角形中，D 、E 分别在、上，且
AD AC =1
3
，＝，则有（ ）
A. △∽△
B. △∽△
C. △∽△
D. △∽△
5、如图，在ABC △中，90C =o ∠，在AB 边上取一点D ，使BD BC =，过D 作DE AB
⊥交AC 于E ，86AC BC ==，．求DE 的长．
A C
D E
第1题图
A
B C E
D
F
第3题图
A
B C E
D
F 第2题图
A
D
C E
第4题图
6、如图，在△中，∠90°，边的垂直平分线交于点E ，交于点F ，⊥，
交于点G ．求证：是与的比例中项．
相似三角形的应用
【知识要点】
1.如何构造相似三角形： (1)利用阳光下的影子:
人的影长
人的高度
旗杆影长旗杆高度
（同一刻时）
(2)利用标杆：
(3)利用镜子反射：
【学堂练习】
1. 小颖测得2m 高的标杆在太阳下的影长为 1.2m,同时又测得一棵树的影长为
3.6m,请你帮助小颖计算出这棵树的高度.
2.如图，有一路灯杆(底部B 不能直接到达)，在灯光下，小明在点D 处测得自己
的影长＝3m ，
B
G
沿方向到达点F处再测得自己得影长＝4m，如果小明得身高为1.6m，求路灯杆的高度。
3. 阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区
到窗口下的墙脚距离8.7m,窗口高1.8m,求窗口底边离地面的高.
【经典例题】
例1、张同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在
某一建筑的墙上，分别测得其长度为9.6米和2米，问学校旗杆的高度
D F
B
C E
G
9.6米
2米
例2、如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且1米，5米，求电视塔的高。
例3、我侦察员在距敌方200米的地方发现敌人的一座建筑物，但不知其高度又不能靠近建筑物测量，机灵的侦察员食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住。
若此时眼睛到食指的距离约为40，食指的长约为8,你能根据上述条件计算出敌方建筑物的高度吗？请说出你的思路。
【随堂练习】
1、如图，一电线杆的影子分别落在了地上和墙上，某一时刻，小明竖起1米高
的直杆，量得其影长为0.5米，此时，他又量得电线杆落在地上的影子长3米，落在墙上的影子的高为2米。
小明用这些数据很快算出了电线杆的高。
请你计算，电线杆的高为（）
（A） 5米（B）6米（C）7米（D）8米
2、如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地
面上形成阴影（圆形）的示意图．已知桌面的直径为1.2米，桌面距离地面1米．若灯泡距离地面3米，则地面上阴影部分的面积为（）．
A．0.36π平方米B．0.81π平方米C．2π平方米D． 3.24π平方米
3、厨房角柜的台面是三角形（如图所示），如果把各边中点连线所围成的三角形
围成黑色大理石（图中阴影部分），其余部分铺成白色大理石，那么黑色大理
石的面积与白色大理石面积的比是（）
A． B． C．
D．
1题
2题
3题
4、小强用这样的方法来测量学校教学楼的高度：如图，在地面上放一面镜子（镜子高
度忽略不计），他刚好能从镜子中看到教学楼的顶端B ，他请同学协助量了镜子与教学楼的距离21米，以及他与镜子的距离2.5米，已知他的眼睛距离地面的高度1.6米，请你帮助小强计算出教学楼的高度。
（根据光的反射定律：反射角等于入射角）
5、如图,甲楼高18米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是
1: 2 ,已知两楼相距20米,那么甲楼的影子落
在乙楼上有多高?
E
D
C A
【课后强化】
1、某学习小组选一名身高为1.6m 的同学直立于旗杆影子的顶端处，其他人分为
两部分，一部分同学测量该同学的影长为1.2m ，另一部分同学测量同一时刻旗杆影长为9m ，那么旗杆的高度是。
2、如图，为了测量水塘边A 、B 两点之间的距离，在可以看
到的A 、B 的点E 处，
取、延长线上的C 、D 两点,使得∥，
若测得＝5m ，＝15m ，3m,
则A 、B 两点间的距离为。
3、如图，是斜靠在墙上的长梯，梯脚B 距墙脚1.6m ，梯上点D 距墙1.4m ，
长0.55m ，求该梯子的长。
A
D C E
4、如图，火焰的光线穿过小孔O ，在竖直的屏幕上形成倒立的像，像的长度为2，60，15，求火焰的长度。
A
C B
D O。