牛顿环测液体折射率实验报告
牛顿环干涉法测量液体折射率的实验研究

牛顿环干涉法测量液体折射率的实验研究
张思慧;辛琨;邹俭英;尹教建;韩立立;周小岩
【期刊名称】《大学物理实验》
【年(卷),期】2016(029)004
【摘要】利用牛顿环干涉法测量了水、乙醇和不同浓度的葡萄糖溶液的折射率,其实验结果与理论值符合的较好。
实验过程中发现选用更大曲率半径的牛顿环能够有效降低干涉条纹的计数难度。
【总页数】3页(P49-51)
【作者】张思慧;辛琨;邹俭英;尹教建;韩立立;周小岩
【作者单位】中国石油大学华东,山东青岛 266580;中国石油大学华东,山东青岛 266580;中国石油大学华东,山东青岛 266580;中国石油大学华东,山东青岛 266580;中国石油大学华东,山东青岛 266580;中国石油大学华东,山东青岛 266580
【正文语种】中文
【中图分类】O4-34
【相关文献】
1.牛顿环干涉实验在液体折射率测量中的应用 [J], 刘敏
2.牛顿环干涉法测定液体折射率装置的设计 [J], 罗龙;李丽荣;毛爱华;刘艳丽
3.用牛顿环干涉测量液体折射率 [J], 李文成;宁亚平;杨津生
4.论牛顿环干涉法测定液体折射率 [J], 关小泉
5.牛顿环法测液体折射率的实验研究 [J], 李晓莉
因版权原因,仅展示原文概要,查看原文内容请购买。
用牛顿环产生的干涉条纹测量液体的折射率

The measurement of liquid refractive index by using interfered stripe of Newton ring
WANG Yu ping
( Department of Physics, Fuling T eachers College, Chong qing, 408003, China)
d 左 / mm d 右 / mm d 左 / mm d 右 / mm d 左 / mm d 右 / mm 40. 242 23. 415 32. 136 17. 508 42. 496 28. 056
r k= ( d 左- d 右) / 2 r 空= 8. 414 r 水= 7. 314 r 酒= 7. 220
Abstract: T he w ays of measuring t he liquid ref ract ive index are discussed t hrough radius of inter f ered st ripe by using ex periment al set of New t on ring Key words: Newt on ring; interference; liquid; refract ive index
第 20 卷第 10 期 2001 年 10 月
大 学 物 理 COL L EGE PHYSICS
Vol. 20 No. 10 Oct. 2001
物理实验
用牛顿环产生的干涉条纹测量液体的折射率
王玉平
( 涪陵师范专科学校 物理系 , 重庆 408003)
摘要 : 提出了用牛顿环实验装置 , 通过测量干涉条纹的半径来测量液体折射率的方法 . 关键词 : 牛顿环 ; 干涉 ; 液体 ; 折射率 中图分类号 : O 436. 1 文献标识码 : A 文章编号 : 1000 0712( 2001) 10 0029 02 牛顿环通常用 来观 察干 涉现 象 , 利用 读数 显微 镜 测量干涉条纹 半径 , 根据 已知 的波长 和干 涉条 纹的 级 数计算透镜的曲率半径 . 其原理装 置如图 3 所 示 . 在 平 板玻 璃 DE 上放 一平凸 透镜 ABC, 在它 们的空 隙中 充 有折射率为 n 的透明 介质 . 平行光 垂直 照射在 平凸 透 镜 ABC 的 A B 面上 , 在介质的上下面形成两 次反射 , 两 次反射之间存 在一定 的光 程差 , 从而 形成 等厚 干涉 条 纹 . 这些干涉条纹是一组以 C 为 圆心的同 心圆 , 如图 4 所示 . 第 k 级干涉条纹的光程差为
干涉法测液体的折射率
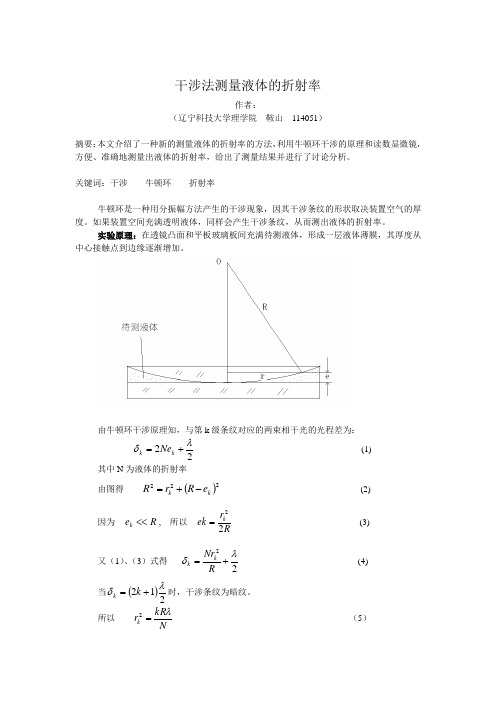
干涉法测量液体的折射率作者:(辽宁科技大学理学院 鞍山 114051)摘要:本文介绍了一种新的测量液体的折射率的方法,利用牛顿环干涉的原理和读数显微镜,方便、准确地测量出液体的折射率,给出了测量结果并进行了讨论分析。
关键词:干涉 牛顿环 折射率牛顿环是一种用分振幅方法产生的干涉现象,因其干涉条纹的形状取决装置空气的厚度。
如果装置空间充满透明液体,同样会产生干涉条纹,从而测出液体的折射率。
实验原理:在透镜凸面和平板玻璃板间充满待测液体,形成一层液体薄膜,其厚度从中心接触点到边缘逐渐增加。
由牛顿环干涉原理知,与第k 级条纹对应的两束相干光的光程差为:22λδ+=k k Ne (1)其中N 为液体的折射率由图得 ()222k k e R r R -+= (2)因为 R e k <<, 所以 Rr ek k 22= (3)又(1)、(3)式得 22λδ+=R Nr k k (4) 当()212λδ+=k k 时,干涉条纹为暗纹。
所以 NkR r k λ=2(5)由于牛顿环中心不是一点,设附加光程差为x ,则()22λδ+±=x Ne k k (6)取m 、n 级暗条纹,直径分别为D m 、D n 。
消去附加光程差x 有 ()224nm D D R n m N --=λ(7) 实验装置:牛顿环装置(mm R 3000=) 读数显微镜(JXD-2型) 钠光灯(nm 3.589=λ) 滴管先把牛顿环装置的凸透镜和平板玻璃拆开,用滴管在平板玻璃上滴一层待测液体,然后压上凸透镜。
由于液体有表面张力,能够充满凸透镜和平板玻璃之间的空间。
(实验只用的液体为水)数据处理:(已知nm 3.589=λ mm R 3000= )222707.52mm D D n m =-()3417.1422=--=nmDD R n m N λ设 22n m D D Z -=()()22148.01662mm ZZU iZ =--=∑令 2.0=-n m U nm U 3.0=λ()%0.2=-++=-nm U U ZU N E nm Z λλ()027.0==N N E U N027.0342.1±=±=N U N N结论:实验中产生误差的主要因素是m 、n 的准确性,求不确定度时令 2.0=-n m U ,这样求出的相对不确定度为 2.0 % ,结果非常准确。
牛顿环测液体的折射率

摘要:由牛顿发现利用用一个曲率半径大的凸透镜和一个平面玻璃相接触,用单色光照射,则出现明暗相间的单色圆环。
这种光学现象被称为“牛顿环”。
利用牛顿环的光学原理测量液体折射率,是一种十分可行的方法,本文中阐述了牛顿环的光学原理和测量蓖麻油折射率的实验原理,并研究出了具体的测量方法,最后对蓖麻油的折射率进行了测量,并得出了较为可靠地数据结果。
English abstract:By Newton found use in a large radius of curvature of the convex lens and a flat glass contact, with monochromatic light illuminate, appear with monochromatic light and shade is ring. This optical phenomenon is known as \"Newton ring\". Using the optical principle of Newton's rings measuring liquid refractive index, is a very feasible method, this article elaborated the Newton ring optical principle and the principle of measuring refractive index of castor oil experiment, and worked out the specific measurement method, finally, the refractive index were measured, castor oil and it is concluded that the more data results in a reliable way.关键词:牛顿环、折射率、逐差法Keywords:Newton's rings, refractive index, by differential method目录摘要 (1)关键词 (1)一、牛顿环 (2)(一)牛顿环简介 (3)(二)牛顿环原理 (3)二、牛顿环测量水的折射率 (5)(一)测量原理 (5)(二)实验测量方法 (5)(三)实验步骤 (5)(四)实验数据及其计算 (6)1、牛顿环测量空气的折射率 (6)2、牛顿环测量水的折射率 (7)3、水的折射率的计算 (8)三、误差分析 (8)四、实验结果及其结论 (9)五、结束语 (10)参考文献 (10)一、牛顿环(一)牛顿环简介17世纪初,物理学家牛顿在考察肥皂泡及其他薄膜干涉现象时,把一个玻璃三棱镜压在一个曲率已知的透镜上,偶然发现干涉圆环,并对此进行了实验观测和研究。
等厚干涉牛顿环实验报告

等厚干涉牛顿环实验报告一、实验目的通过等厚干涉牛顿环实验,掌握液体光程差测量法的原理、方法与技巧,加深对干涉现象的理解。
二、实验原理1、干涉现象:两个波长相等的光波相交时,在相交区域内会出现明暗相间的干涉条纹现象,称为干涉现象。
2、等厚干涉:同一透明介质中,光线经过的路程相等,产生干涉现象。
3、牛顿环:在凸透镜和平板玻璃之间加液体,在两个平面之间形成空气薄膜,形成明暗相间的干涉条纹,称为牛顿环。
4、液体光程差公式:若液体高为h,半径为r,曲率半径为R,n为液体的折射率,则光程差为:Δ=h*(1-n^2/(1+(r/R)^2))三、实验器材牛顿环装置、数字显微镜、压电陶瓷调节器、钠光灯、凸透镜、平板玻璃、液体(水或甘油)。
四、实验步骤1、将牛顿环装置放平,并在顶上固定凸透镜。
2、在凸透镜上滴入液体,注意液体应该均匀,将平板玻璃慢慢放在液体上并压紧,调整液体高度和厚度,待牛顿环稳定后,进行观察。
3、使用数字显微镜,在环的中央测量各环的直径,注意要取多组数据。
4、根据公式计算出各环的半径,计算出液体的折射率。
5、重复以上步骤,取不同液体,比较其折射率。
五、实验注意事项1、注意平板玻璃和凸透镜的清洁,避免出现指纹、灰尘等污染物,影响实验结果。
2、滴液时注意液滴均匀,避免产生空气袋。
3、测量时注意数字显微镜的读数准确。
4、实验过程中要小心,避免出现液体溅出等安全问题。
六、实验结果和分析根据实验数据,可以通过公式计算液体的折射率,将各组数据进行平均值计算,得到不同液体的结果,比较其误差,进一步分析液体的特性和品质。
七、实验总结通过等厚干涉牛顿环实验,掌握了液体光程差测量法的原理、方法与技巧,加深了对干涉现象的理解。
同时,也提高了实验能力和思维能力,为今后科研实践打下了基础。
用牛顿环对比法测液体的折射率_郭小花

( k=0, 1, 2…)
( 1)
式中e为某一暗纹中心所在处的液体膜厚度, k 为干涉级次。
利用图1中的几何关系, 可得e≈ r2 ( r为条纹 2R
半径) , 代入 ( 1) 式, 有
( k=0, 1, 2…)
( 2)
图1 牛顿环实验装置
如图1所示, 我们把一个曲率半径很大的平凸 透 镜AOB放 在 一 块 滴 有 少 许 液 体 的 平 面 玻 璃 板 D 上, 二者之间形成一层厚度不均匀的液体薄层 ( 设 其折射率为n) , 接触点为O, 当光近乎垂直地照射 到薄膜上时, 在整个视场内光线的入射角可视为不 变的常数, 则反射光在相遇点的相位差只决定于产 生该反射的薄膜厚度。薄膜上厚度相同的地方反射 光所产生的光程差相同, 因此等厚干涉条纹的形状 是 薄 膜 上 等 厚 度 点 的 轨 迹 。 [1]在 牛 顿 环 中 , 干 涉 条纹是一组以O为中心的同心圆环。
( 4)
rk2=
kRλ n
( 5)
两式相减, 得平凸透镜的曲率半径
R= (rm2- rk2) n
( 6)
(m- k) λ
观察牛顿环时我们也将会发现, 牛顿环中心由
于形变、灰尘、水等的影响, 中心不是一点, 而是
一 个 不 甚 清 晰 的 暗 或 亮 的 圆 斑 。 [3]因 而 圆 心 不 易
确定, 故常取暗环的直径替换, 进而有
2.2 把平凸透镜压到滴水的光学玻璃上, 则它 和平面玻璃板之间形成了液体膜。将此装置放到显 微镜的载物台上, 调节手轮, 使显微镜由低向高缓 慢移动, 直至在目镜中看到清晰的干涉条纹为止。 由于液体膜压得不会很均匀, 故在视场中的某个地 方会出现一小块空气膜, 其干涉花样如图2所示。
利用牛顿环测液体折射率

利用牛顿环测液体折射率摘要:液体折射率的测量在工农业中十分重要,本文阐述了牛顿环测液体折射率的实验原理,通过比较空气与水中牛顿环半径,求出液体折射率。
本文采用逐差法处理数据,测量过程简单,结果较为准确关键词:牛顿环 液体折射率 逐差法牛顿环是一种典型的等厚薄膜干涉现象,能充分显示光的波动性。
本文通过研究对比空气和水在牛顿环里发生的干涉现象,更新了液体折射率的测试方法,使牛顿环的应用更加丰富,开拓了物理实验的新视野。
一,当牛顿环薄膜为一般介质的讨论如图所示,设距接触点为r处薄膜厚度为d,设薄膜折射率为N.一束单色光垂直投射上去,入射光在薄膜上下表面反射并与上表面发生干涉,两束光光程差为:=22dn λδ+------------------------------------------(1)在反射光中形成一系列以接触点O为中心的明暗相间的同心圆圈(如图b所示)叫牛顿圈。
其中2λ项是膜层下表面光由光疏介质到光密介质交界面反射时所引起的半波损失。
满足明、暗圈的干涉条件分别是: 22dN k λδλ=+=――――――――――――(2)K=1,2,3……2(21)22dN k λλδ=+=+-----------------------------(3)由图a 几何关系可知: 222()R r R d =+-即: 222r Rd d =-其中R 为透镜曲率半径。
由于R>>d,所以上式近似为:22r Rd = ——————————————(4)代入明暗圈公式有:2(21)2k k R r N λ+=(明圈)————————(5)2kR r Nλ=(暗圈)———————————(6) 由上式知,圈半径越大,相应的干涉级别越高。
随着圈半径增大,薄膜上下层两面间夹角增大,条纹变密。
实际观察到的牛顿环中心不是一点, 而是一个亮圆斑或者暗圆斑。
这是因为透镜的凸面与平面玻璃接触时受压而发生的弹性形变, 接触处是一个圆面, 或者是由于透镜与平面玻璃之间有尘埃, 造成两玻璃面未接触上。
牛顿环法测液体折射率的实验研究

牛顿环法测液体折射率的实验研究折射,一种光的自然现象,它的发生依赖于光的波长,以及光折射介质的折射率。
折射率,一种介质的物理量,它决定了光在介质中传播时发生的折射程度,以及光在介质中传播时被改变的波长。
而在本文中,我们将聚焦于探讨牛顿环法在测量液体折射率方面的研究。
牛顿环法是科学家发明的一种用来测量折射率的方法。
牛顿环法包括三个步骤:先用现成的玻璃片做半透镜,然后放在一个有反射环的容器中,最后将容器放置在一个照明设备的照射下。
当照射的光线被半透镜反射到反射环上时,一条光线就会被反射到另一边的反射环上,这条光线被称为真实线。
然后将液体放入容器中,当液体反射的光线穿过液体时,它会发生折射,折射的光线称为反射线。
当真实线和反射线分别出现在反射环上时,从里面测试发现他们会有一定量的角度偏移,这个角度偏移就是液体折射率的测量值。
牛顿环法过程中涉及到的各种因素会对测量结果产生影响,例如物体的表面粗糙程度,物体的折射角等等。
若物体表面存在粗糙程度,那么光辐射就会发生反射,影响对物体表面光折射率的测量。
此外,假如物体表面折射角大于90°,就会发生全反射,因此无法通过牛顿环法测量物体折射率。
为了尽可能准确地测量液体折射率,应该采取一定的措施,确保物体表面粗糙程度尽可能小,而且物体表面的折射角应小于90°,有助于获得准确的测量结果。
折射率的测量精度受多种因素的影响,比如照明设备的光强,以及反射环的折射率。
所以为了确保测量结果的准确性,应该使用较强的光源,而且反射环的折射率应尽量接近样本,这样可以提高测量结果的准确性。
在本文中,我们着重探讨了牛顿环法在测量液体折射率方面的应用。
牛顿环法是一种简便而有效的方法,能够准确测量出液体的折射率,并且特殊器件不多,常见的玻璃片和反射环就可以搭建出一个实验装置。
另外,牛顿环法有一系列特定的条件,必须要满足,才能得到准确的测量结果,例如物体表面的粗糙程度,以及物体的折射角等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用牛顿环测液体的折射率
【摘要】本文结合牛顿环干涉原理测量空气折射率的方法,阐述了测量液体折射率的实验原理,并研究出了具体的测量方法,最后对水的折射率进行了测量,并得出了较为准确的测量结果。
一、实验目的:
牛顿环是一种典型的等厚薄膜干涉现象,能充分显示光的波动性。
本文通过研究对比空气和水在牛顿环里发生的干涉现象,更新了液体折射率的测试方法,使牛顿环的应用更加丰富,开拓了物理实验的新视野。
二、设计原理
当以波长为x 的钠黄光垂直照射到平凸透镜上时,由液体膜上,下表面反射光的光程差以及干涉相消。
即暗纹条件:
式中e 为某一暗纹中心,所在处的液体膜厚度,k 为干涉级次。
利用图中的几何关系,可得:R r e 2/2
= (r 为条纹半径),代入(1)式,有
......)
2,1,0(2/)12(2//2=+=+=n n R nr λλδ (2)
则暗纹半径......)2,1,0(/==n k nR r k
λ (3)
若取暗纹观察,则第m ,k 级对应的暗环半径的平方 n mR r m /2
λ= (4) k nR r n /2λ= (5)
两式相减得平凸透镜的曲率半径)/()(2
2
n m n r r R n m --= (6)
观察牛顿环时我们也将会发现牛顿环中心由于形变,灰尘,水等的影响,中心不是一点,而是一个不甚清晰的暗或亮的圆斑。
目因而圆心不易确定。
故常取暗环的直径替换。
进而有
λ)(4/)(22n m n D D R n m --= (7)
同理对于空气膜。
则有λ)(4/2
'2'n m D D R n m --= (8)
式(7)与式(8)相比,可得:)/()(2
2
2
'2
'n m n m D D D D n --= (9)
由(9)式可知,只要测出同一装置(相同的平凸透镜和平面的玻璃板)下的空气膜和液体膜的条纹直径,即可求出液体的折射率。
三、设计方案 1.调整实验装置
将牛顿环装置放在毛玻璃上。
点燃钠光灯,调节显微镜前面的透光反射镜的角度,与水平面成0
45的角度,这样从目镜中看到明亮的光场旋转目镜旋钮,使分化板上的十字线位于目镜的交线上,即从目镜中看到清晰地十字线。
缓慢转动手轮,使显微镜自下而上缓慢上移,直到从目镜中看到清晰地干涉图样,并使相与交叉丝无视差。
略微移动牛顿环装置,使显微镜十字叉丝位于牛顿环中心。
2.实验操作
将牛顿环装置的凸透镜和平板玻璃拆开,用滴管在平板玻璃上滴一层待测液体,然后压上凸透镜。
由于
液体有表面张力,能够充满凸透镜和平板玻璃之间的空间。
则现在凸透镜和平板玻璃之间形成了液体膜。
将此装置放到显微镜的载物台上,调节手轮,使显微镜由低到高缓慢移动,直至在目镜中看到清晰地干涉条纹为止。
由于液体膜压得不会很均匀。
故在视场中的某个地方会出现一小块空气膜,其干涉花样如上面右图所示。
四、实验结果与分析 4.1数据记录
测量空气薄膜的牛顿环数据
数据表取m-n=25 ,仪器误差:0.005mm 室温9C 0
环数
(mm)
环数
(mm)
)mm (2
m (mm) (mm) n (mm) (mm)
55 30.683 19.558 11.125 30 29.345 20.886 8.459 52.211
52.497
±0.340
890.8
±5.8
50 30.444 19.794 10.650 25 29.024 21.216 7.808 52.458
45 30.187 20.045 10.142 20 28.663 21.558 7.105 52.379 40 29.945 20.308 9.637 15 28.273 21.949 6.342 52.650
35 29.643 20.599 9.044 10 27.815 22.421 5.394 52.699
测量蒸馏水薄膜的牛顿环数据
数据表取m-n=25 ,仪器误差:0.005mm 室温9C 0
环数
(mm)
环数
(mm)
)mm (2
m
(mm) (mm) n (mm) (mm)
55 29.998 20.239 9.759 30 28.828 21.408 7.420 40.182
40.384
±0.390
50 29.789 20.447 9.342 25 28.543 21.694 6.849 40.364
45 29.566 20.670 8.896 20 28.234 22.003 6.232 40.301
40 29.345 20.891 8.454 15 27.899 22.336 5.563 40.523 35 29.085 21.152 7.933 10 27.483 22.752 4.731 40.550
4.2数据处理
在空气薄膜状态下
(1)确定平凸透镜凸面曲率半径的最佳值
令
(3)不确定度计算
A类不确定度:
B类不确定度:
仪器误差:Δ
=0.005mm
仪
注:取值最大值,=D
=11.125mm,
55
故
(4)写出实验结果:
相对不确定度:
百分差:
水膜时牛顿环的曲率半径计算
令
曲率半径最佳值
(3)不确定度计算
A类不确定度:
B类不确定度:
仪器误差:Δ
=0.005mm
仪
=9.759mm,
注:取值最大值,=D
55
故
(4)写出实验结果:
相对不确定度:
百分差:
计算水的折射率: n 的相对误差为 n 的绝对误差为 所以水的折射率为
4.3 误差分析
查蒸馏水折射率表格可得在10C 0
为1.33369 ,对比试验结果以十分接近了。
计算百分差:%6.2%100334
.1334
.1299.1%100n n n =⨯-=⨯-=
标准标准R E 误差很低所以该方法测液体可行。
而引起误差的主要原因是: (1)仪器存在误差
(2)在实验时是9C 0
与查表的10C 0
有点区别
(3)做实验时数实验视样时环数数错了,显微镜叉丝与显微镜移动时的方向不平行等。
从误差分析中我们可以知道在做实验时我们要做到小心谨慎以避免个人误差的产生。
5.结束语
该实验是对牛顿环实验的深入探索,利用牛顿环的干涉进行测量液体的折射率。
通过本次实验让我们对于牛顿环有了更深的了解,也使我知道一个道理做实验时小心谨慎是很重要的。
这个实验也让我们开拓了自己的想象力。
