信号与线性系统分析课后答案_吴大正
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
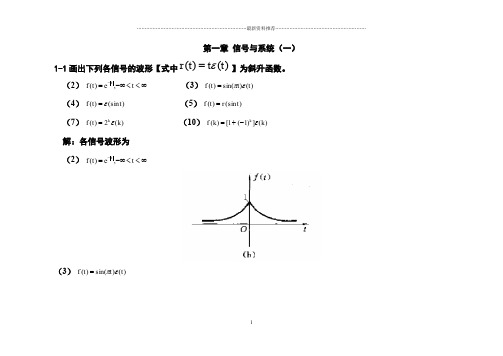
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析(吴大正第四版)习题答案

第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析吴大正习题答案

请浏览后下载,资料供参考,期待您的好评与关注!专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=请浏览后下载,资料供参考,期待您的好评与关注!解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r(t(sin)(7))f kε=t(k2)(请浏览后下载,资料供参考,期待您的好评与关注!请浏览后下载,资料供参考,期待您的好评与关注!(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f请浏览后下载,资料供参考,期待您的好评与关注!(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f请浏览后下载,资料供参考,期待您的好评与关注!(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ请浏览后下载,资料供参考,期待您的好评与关注!(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
信号与线性系统分析-(吴大正-第四版)习题答案

信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线,性系统分析,(吴大正,全8章),习题答案

西安电子科技大学844信号与系统第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析_(吴大正_第四版)习题答案

第四章习题
4.6求下列周期信号的基波角频率Ω和周期T。
(1) (2)
(3) (4)
(5) (6)
4.7用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-15
(3) (4)
(5)
1-25设激励为 ,下列是各系统的零状态响应 。判断各系统是否是线性的、时不变的、因果的、稳定的?
(1) (2) (3)
(4) (5) (6)
(7) (8)
1-28某一阶LTI离散系统,其初始状态为 。已知当激励为 时,其全响应为
若初始状态不变,当激励为 时,其全响应为
若初始状态为 ,当激励为 时,求其全响应。
1-10计算下列各题。
(1) (2)
(5) (8)
1-12如图1-13所示的电路,写出
(1)以 为响应的微分方程。
(2)以 为响应的微分方程。
1-20写出图1-18各系统的微分或差分方程。
1-23设系统的初始状态为 ,激励为 ,各系统的全响应 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1) (2)
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。如果是,确定其周期。
(2) (5)
解:
1-6已知信号 的波形如图1-5所示,画出下列各函数的波形。
(1) (2) (5) (6)
(7) (8)
解:各信号波形为
(1)
(2)
(5)
(6)
(7)
(8)
1-7已知序列 的图形如图1-7所示,画出下列各序列的图形。
信号与线性系统分析_(吴大正_第四版)习题答案
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])1)1[1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与线性系统分析课后答案_吴大正第一章r(t),t,(t)1-1画出下列各信号的波形(式中)为斜升函数。
解:各信号波形为,t (2)f(t),e,,,,t,,(3) f(t),sin(,t),(t)(4) f(t),,(sint)(5) f(t),r(sint)k(7) f(t),2,(k)k(10) f(k),[1,(,1)],(k)r(t),t,(t)1-2 画出下列各信号的波形[为斜升函数]。
f(t),r(t),2r(t,1),r(t,2)f(t),2,(t,1),3,(t,1),,(t,2) (1) (2) f(k),k[,(k),,(k,5)]f(t),r(2t),(2,t) (5) (8),kkf(k),sin()[,(k),,(k,7)]f(k),2[,(3,k),,(,k)](11) (12) 6解:各信号波形为f(t),2,(t,1),3,(t,1),,(t,2) (1)f(t),r(t),2r(t,1),r(t,2) (2)f(t),r(2t),(2,t) (5)f(k),k[,(k),,(k,5)] (8),kf(k),sin()[,(k),,(k,7)](11) 6kf(k),2[,(3,k),,(,k)](12)1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
3,,,,f(t),3cost,2sin(,t)f(k),cos(k,),cos(k,) (2) (5) 524436 解:f(t)1-6 已知信号的波形如图1-5所示,画出下列各函数的波形。
f(0.5t,2)f(1,2t)f(t,1),(t)f(t,1),(t,1) (1) (2) (5) (6) tdf(t)f(x)dx (7) (8) ,,,dt解:各信号波形为f(t,1),(t) (1)f(t,1),(t,1) (2)f(1,2t) (5) f(0.5t,2) (6)df(t)(7) dttf(x)dx (8) ,,,f(k)1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
f(k,2),(k)f(k,2),(k,2) (1) (2)f(,k,2)f(k,2)[,(k),,(k,4)] (3) (4) f(,k,2),(,k,1)f(k),f(k,3) (5) (6) 解:df(t)f(t)1-9 已知信号的波形如图1-11所示,分别画出和的波形。
dtf(3,2t)f(3,t)f(3,t)解:由图1-11知,的波形如图1-12(a)所示(波形是由对的波形展宽为原来f(3,t)f(t,3)f(t,3)的两倍而得)。
将的波形反转而得到的波形,如图1-12(b)所示。
再将的波形右df(t)f(t)移3个单位,就得到了,如图1-12(c)所示。
的波形如图1-12(d)所示。
dt1-10 计算下列各题。
2d,td(1,t)[e,(t)],,,,cost,sin(2t),(t) (1) (2) 2dtdtt,,t2(1,x),'(x)dx[t,sin()],(t,2)dt (5) (8) ,,,,,,41-12 如图1-13所示的电路,写出u(t)(1)以为响应的微分方程。
Ci(t)(2)以为响应的微分方程。
L1-20 写出图1-18各系统的微分或差分方程。
y(,)f(,)x(0)1-23 设系统的初始状态为,激励为,各系统的全响应与激励和初始状态的关系如下,试分析各系统是否是线性的。
tt,ty(t),f(t)x(0),f(x)dxy(t),ex(0),sinxf(x)dx (1) (2) ,,00tky(k),(0.5)x(0),f(k)f(k,2)y(t),sin[x(0)t],f(x)dx (3) (4) ,0ky(k),kx(0),f(j), (5),0jy(,)f(,)1-25 设激励为,下列是各系统的零状态响应。
判断各系统是否是线性的、时不变的、因果的、zs稳定的,dft()y(t),f(t)y(t),f(t)cos(2,t)yt(), (1) (2) (3) zszszsdty(t),f(,t)y(k),f(k)f(k,1)y(k),(k,2)f(k) (4) (5) (6) zszszsky(k),f(j)y(k),f(1,k)(7) (8) ,zszs,0j1-28 某一阶LTI离散系统,其初始状态为。
已知当激励为时,其全响应为y(k),,(k)x(0)1k若初始状态不变,当激励为时,其全响应为 y(k),[2(0.5),1],(k),f(k)2若初始状态为,当激励为时,求其全响应。
2x(0)4f(k)第二章2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1) y''(t),5y'(t),6y(t),f(t),y(0),1,y'(0),,1,(4) y''(t),y(t),f(t),y(0),2,y'(0),0,y(0)y'(0)02-2 已知描述系统的微分方程和初始状态如下,试求其值和。
,,,(2) y''(t),6y'(t),8y(t),f''(t),y(0),1,y'(0),1,f(t),,(t),,2t (4) y''(t),4y'(t),5y(t),f'(t),y(0),1,y'(0),2,f(t),e,(t),,解:2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
,ty''(t),4y'(t),4y(t),f'(t),3f(t),y(0),1,y'(0),2,f(t),e,(t) (2) ,, 解:i(t)u(t)2-8 如图2-4所示的电路,若以为输入,为输出,试列出其微分方程,并求出冲激响应和阶跃响SR应。
u(t)2-12 如图2-6所示的电路,以电容电压为响应,试求其冲激响应和阶跃响应。
C2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
f(t)*f(t)f(t)*f(t)f(t)*f(t) (1) (2) (3) 131412f(t)*f(t)*f(t)f(t)*[2f(t),f(t,3) (4) (5) 143122波形图如图2-9(a)所示。
波形图如图2-9(b)所示。
波形图如图2-9(c)所示。
波形图如图2-9(d)所示。
波形图如图2-9(e)所示。
f(t),t,(t)y(t),f(t)*f(t,1)*,'(t,2)f(t),,(t),,(t,2)2-20 已知,,求1122,2(tx),,y(t),ef(x,2)dxy(t)f(t)2-22 某LTI系统,其输入与输出的关系为 ,t1,h(t)求该系统的冲激响应。
f(t),,(t)2-28 如图2-19所示的系统,试求输入时,系统的零状态响应。
2-29 如图2-20所示的系统,它由几个子系统组合而成,各子系统的冲激响应分别为h(t),,(t),,(t,3)h(t),,(t,1) ba求复合系统的冲激响应。
第三章习题0,,k,k1f(i)3.1、试求序列的差分、和。
f(k)=,,,f(k),f(k),,,,i=-,,2,,,3.6、求下列差分方程所描述的LTI离散系统的零输入相应、零状态响应和全响应。
ykykfkfkky()-2(-1)(),()2(),(-1)-1,,,,1)ykykfkfkkky()2(-1)(),()(34)(),(-1)-1,,,,,,3)5)1kykykykfkfkkyy,,,,,,,()2(-1)(-2)(),()3()(),(-1)3,(-2)-523.8、求下列差分方程所描述的离散系统的单位序列响应。
ykykfk()-(-2)(), 2)ykykykfk()-4(-1)8(-2)(),, 5)3.9、求图所示各系统的单位序列响应。
(a)(c)3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
fkfkfk()-()(),(1)(2)(3)(4) fkfk()(),fkfk()(),fkfk()(),,,2131223343.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
kgkk()0.5,,3.15、若LTI离散系统的阶跃响应,求其单位序列响应。
,,,,kfkk()0.5(),,3.16、如图所示系统,试求当激励分别为(1) (2)时的零状态响应。
fkk()(),,,,k,khkk=,fkkak=--1,,3.18、如图所示的离散系统由两个子系统级联组成,已知,,激励,hk=2cos,,,,,,,,,,,,21a4求该系统的零状态响应。
(提示:利用卷积和的结合律和交换律,可以简化运算。
) ()kyzshkk=,hkk=-5,3.22、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为,,求复合,,,,,,,,12系统的单位序列响应。
第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T。
,j100t (1) (2) cos[(t,3)]e2cos(2t),sin(4t)cos(2,t),cos(3,t),cos(5,t) (3) (4),,,,, (5) (6) cos(t),sin(t)cos(t),cos(t),cos(t)242354.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压如图4-19所示, u(t)(1)求的三角形式傅里叶系数。
u(t)1(2)利用(1)的结果和,求下列无穷级数之和 u(),12111 S,1,,,,......357(3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和111 S,1,,,, (222357)图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换,sin[2(t,2)] (1)f(t),,,,,t,, ,(t,2),2f(t),,,,,t,,22 (2) ,,t2,sin(2t),, f(t),,,,,t,, (3),,,2t,,4.18 求下列信号的傅里叶变换,jt,3(t,1)(1) (2) f(t),e,(t,2)f(t),e,'(t,1)2,2t(3) (4) f(t),sgn(t,9)f(t),e,(t,1)t(5) f(t),,(,1)24.19 试用时域微积分性质,求图4-23示信号的频谱。
