单因素敏感分析案例
单因素敏感性分析

单因素敏感性分析题目:
某投资方案设计年生产能力为10万台,计划总投资为1200万元,期初一次性投入,当年年底便产生收益。
预计产品价格为35元/台,年经营成本为140万元,方案寿命期为10年,到期时预计设备残值收入为80万元,基准收益率为10%。
试以NPV指标就投资额、单位产品价格、经营成本对该投资方案作单因素敏感性分析。
(影响因素分别按±10%、±20%变动,绘制敏感性分析图并计算平均敏感系数进行敏感性因素排序)。
可以这样理解
第一年,年初的时间点为0,年末时间点为 1
第二年,年初的时间点为1,年末时间点为 2
依次类推,N年初的时间点为N-1,N年末的时间点为N.。
单因素敏感性分析方法

单因素敏感性分析方法设投资额为K,年销售收入为S,年经营成本为C,年增值税金为T,期末资产残值为SV,净现值为:NPV=-K+(S-T-C) (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,11)设投资额变动的百分比为X,其变动后的净现值为:NPV=-K(1+X)+(S-T-C) (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,10)设经营成本的变动的百分比为Y,其变动后的净现值为:NPV=-K+[S-T-C(1+Y)] (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,)设产品价格变动的百分比为Z,由于增值税金为销售收入的17%再减去进项税,产品价格的变动不仅引起销售收入的变动,同时还会导致增值税金的变化,由于销售收入与产品价格变动的比例是相同的,所以产品价格变动后的净现值为:NPV=-K+[0.83S(Z+1)-T-C] (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,10)多因素敏感性分析单因素敏感性分析实质上是假设各影响因素之间不相关的前提下针对单个因素进行的,但是,各因素之间往往存在着互相依赖的关系,一个因素的变动会引起其它因素的变动,如国际市场上石油价格的上涨会导致代替石油燃料的电动车的价格上升,另外一个方面,石油价格的上涨也会引起其它生产资料价格的上涨从而导致生产成本的增加。
多因素敏感性分析将克服单因素敏感性分析的局限性,能够反映两个或者两个以上的因素同时变化的结果。
考虑投资额与经营成本同时变动,变动后方案的净现值为:NPV=-K(1+X)+[S-T-C(1+Y)] (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,10)如果考虑投资额、经营成本和产品价格这三个因素的变动,则变动后的净现值为:NPV=-K(1+X)+[0.83S(1+Z)-T-C(1+Y)] (P/A,10%,10) (P/F,10%,1)+SV(P/F,10%,10)倘若荆轲不是刺客,也就更不可能身如飘蓬,居无定所,也许不可能遇见高渐离,所有一切都是冥冥之中的注定吧!“风萧萧兮,易水寒,壮士一去兮,不复还。
灵敏度分析案例范文

灵敏度分析案例范文Sensitivity analysis is a crucial tool in the field of decision-making and risk management. Sensitivity analysis can be applied to various scenarios, such as financial modeling and project management, to evaluate the impact of changes in input variables on the output of a decision model. By conducting sensitivity analysis, decision-makers can gain a better understanding of the uncertainties and risks associated with their decisions, and make more informed choices.敏感度分析是决策和风险管理领域中一个至关重要的工具。
敏感度分析可以应用于各种场景,比如财务建模和项目管理,用于评估输入变量的变化对决策模型输出的影响。
通过进行敏感度分析,决策者可以更好地了解与决策相关的不确定性和风险,并做出更明智的选择。
One perspective to consider is the importance of sensitivity analysis in financial modeling. In financial modeling, sensitivity analysis is used to assess the impact of changes in key inputs, such as interest rates, exchange rates, and commodity prices, on the financial performance of a project or investment. By conducting sensitivity analysis, financial analysts and decision-makers can identify the mostcritical variables that drive the financial outcomes and make adjustments to mitigate risks and uncertainties.有一个角度要考虑的是敏感度分析在财务建模中的重要性。
2020年财务管理案例集:第四章项目投资决策-敏感性分析算例

项目投资决策——敏感性分析敏感性分析就是研究项目的评价结果对影响项目的各种因素变动敏感性的一种分析方法。
例如,当销售量、价格、成本等发生变动时,项目的净现值和内部收益率会发生不同程度的变化。
因素敏感性分析的步骤: ①选取不确定因素一般来说,投资额、产品价格、产品产量、经营成本、项目寿命期、折现率率和原材料价格等因素经常会被作为影响财务评价指标的不确定因素。
②设定不确定性因素的变化程度一般选取不确定因素变化的百分率,通常选择±5%,±10%,±15%,±20%等。
③选取分析指标敏感性分析指标就是确定要考察其不确定性的经济评价指标,一般有净现值、内部收益率和投资回收期等。
④计算敏感性指标第一,敏感度系数。
敏感度系数是反映项目效益对因素敏感程度的指标。
敏感度系数越高,敏感程度越高。
计算公式为:AE F∆=∆ 式中,E 为经济评价指标A 对因素F 的敏感度系数;F ∆为不确定性因素F 的变化率(%);A ∆为不确定性因素F 变化F ∆时,经济评价指标A 的变化率(%)。
第二,临界点。
临界点是指项目允许不确定因素向不利方向变化的极限点。
⑤绘制敏感性分析表和敏感性分析图 ⑥对敏感性分析结果进行分析【例】 G 公司有一投资项目,其基本数据如下表所示。
假定投资额、年收入、折现率为主要的敏感性因素。
试对该投资项目净现值指标进行单因素敏感性分析。
敏感性分析基础数据解:(1)敏感性因素与分析指标已经给定,我们选取±5%,±10%作为不确定因素的变化程度。
(2)计算敏感性指标。
首先计算决策基本方案的NPV ;然后计算不同变化率下的NPV 。
NPV=-100000+(60000-20000)×(P/A,10%,5)+10000×(P/F,10%,5)=57840.68不确定因素变化后的取值不确定因素变化后NPV 的值当投资额的变化率为-10%时,A ∆=67840.68-57840.6857840.68= 17.3%A E F ∆=∆=17.3%-10%= -1.73其余情况计算方法类似。
敏感性分析案例
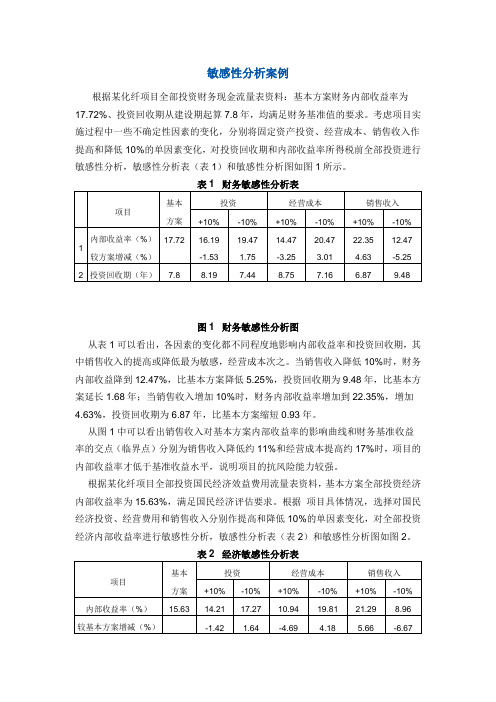
敏感性分析案例根据某化纤项目全部投资财务现金流量表资料:基本方案财务内部收益率为17.72%、投资回收期从建设期起算7.8年,均满足财务基准值的要求。
考虑项目实施过程中一些不确定性因素的变化,分别将固定资产投资、经营成本、销售收入作提高和降低10%的单因素变化,对投资回收期和内部收益率所得税前全部投资进行敏感性分析,敏感性分析表(表1)和敏感性分析图如图1所示。
图1 财务敏感性分析图从表1可以看出,各因素的变化都不同程度地影响内部收益率和投资回收期,其中销售收入的提高或降低最为敏感,经营成本次之。
当销售收入降低10%时,财务内部收益降到12.47%,比基本方案降低5.25%,投资回收期为9.48年,比基本方案延长1.68年;当销售收入增加10%时,财务内部收益率增加到22.35%,增加4.63%,投资回收期为6.87年,比基本方案缩短0.93年。
从图1中可以看出销售收入对基本方案内部收益率的影响曲线和财务基准收益率的交点(临界点)分别为销售收入降低约11%和经营成本提高约17%时,项目的内部收益率才低于基准收益水平,说明项目的抗风险能力较强。
根据某化纤项目全部投资国民经济效益费用流量表资料,基本方案全部投资经济内部收益率为15.63%,满足国民经济评估要求。
根据 项目具体情况,选择对国民经济投资、经营费用和销售收入分别作提高和降低10%的单因素变化,对全部投资经济内部收益率进行敏感性分析,敏感性分析表(表2)和敏感性分析图如图2。
图2 经济敏感性分析图从表2中可以看出,各因素的变化对内部收益率均有一定的影响,其中,销售收入的影响最大,经营费用的影响次之,投资成本的影响较小。
从图2可以看出,内部收益率达到临界点时各因素允许变化的最大幅度分别为:固定资产投资提高的临界点为28.3%,经营费用提高的临界点为7.8%,销售收入降低的临界点为5.6%。
说明该项目能承担一定的风险。
敏感性分析计算范文

敏感性分析计算范文一、单因素敏感性分析单因素敏感性分析是指当改变一个参数或假设时,观察结果的变化。
它通常用于研究一个模型中一些关键参数的影响程度,可以帮助我们确定该参数对结果的敏感性。
1.参数范围法:在单因素敏感性分析中,最常用的方法是确定参数的范围,并在这个范围内改变参数的值,观察结果的变化情况。
这可以通过设置参数的上下限来实现。
例如,假设有一个收益模型,其中一个参数是市场份额,可以设定市场份额的范围为0到100%,然后逐步改变市场份额的值,观察收益的变化情况。
通过这种方法,可以确定市场份额对收益的影响程度。
2.一点敏感性分析:在一点敏感性分析中,我们只改变一个参数的值,其他参数保持不变。
这可以通过增加或减少参数的值来实现。
例如,假设有一个成本模型,其中一个参数是人力成本,可以改变人力成本的值,观察成本的变化情况。
通过这种方法,可以确定人力成本对成本的影响程度。
二、多因素敏感性分析多因素敏感性分析是指当改变多个参数或假设时,观察结果的变化。
它通常用于研究多个因素同时对结果的影响程度,可以帮助我们了解这些因素之间的相互作用。
1.参数组合法:在多因素敏感性分析中,最常用的方法是选取一组关键参数,并在这些参数的可能取值范围内进行组合。
例如,假设有一个销售模型,其中关键参数包括市场规模、市场份额和销售价格,可以选取不同的市场规模、市场份额和销售价格的组合,观察销售额的变化情况。
通过这种方法,可以确定这些参数之间的相对重要性。
2.灵敏度指数法:在灵敏度指数法中,我们可以计算每个参数对结果的影响程度。
这可以通过计算参数的偏导数来实现。
假设有一个利润模型,其中关键参数包括销售额、成本和税率,可以计算销售额、成本和税率对利润的偏导数,然后将它们标准化,得到一个灵敏度指数。
通过这种方法,可以确定哪个参数对利润的影响程度最大。
总结起来,敏感性分析是一种重要的决策工具,可以帮助我们了解模型中不确定因素对结果的影响程度,并为决策提供更全面的信息。
单因素变动敏感性分析

单位变动成本对利润的影响比单价要小,单位变动成本每 上升1%,利润将减少6%。
-10-
单因素变动敏感性分析
分析各参数变化对利润变化的影响程度 固定成本的敏感程度 设固定成本增长2%,则:
固定成本=4000×(1+2%)= 4080万元 按此固定成本计算,利润为:
利润=10 ×(2500-1800)- 4080=2920万元 利润原先是3000元,其变化率为: 利润值变动百分比=(2920-3000) ÷ 3000= -2.6% 敏感系数= -2.6%÷2%= -1.3 固定成本每上升1%,利润将减少1.3%。
• 通过分析公司的历史经营数据,我公司的利润影 响因素敏感系数最高的是价格。在此情况下,经 营者在决策时,提高利润首先要考虑提高销售价 格,或者通过改变产品的品种结构提高高附加值 啤酒的销售
-12-
单因素变动敏感分析表
因素变动 销量 单价
单位变动成本 固定成本
因素变动 销量 单价
单位变动成本 固定成本
-2% 9.8
2,450 1,764 3,920
-2% 2,860 2,500 3,360 3,080
-1% 9.9
2,475 1,782 3,960
-1% 2,930 2,750 3,180 3,040
0% 10
2,500 1,800 4,000
0% 3,000 3,000 3,000 3,000
销售量每上升1%,利润将增加2.3%。敏感系数绝对值大 于1,所以销售量为敏感因素。
单因素不确定性分析例题

1
投资
25.10%
第1年: 2502万元;
第2年: 1251万元
2
销售收入
-9.62%
第3年: 903.85万元 第4年: 1265.39万元 第5-8年: 2149.24万元
9.3
9.3.2单因素敏感性分析
敏感性分析
⑹编制敏感度系数和临界点分析表,并进行结果分析。
敏感度系数和临界点分析表
序号 不确定因素 基本方案 -20% -15% -10% -5% 5% 10% 15% 20% -20% -15% -10% -5% 5% 10% 15% 20% 不确定因素 变化率 净现值 (万元) 664 1383 1203 1023 844 484 304 124 -55 971 890 812 736 594 527 462 399 敏感度 系数 - 50414 -5.412 -5.407 -5.422 -5.422 -5.422 -5.422 -5.414 -2.312 -2.269 -2.229 -2.169 -2.108 -2.063 -2.028 -1.995 临界点 % 临界值
⑶ 以NPV作为经济效益评价指标,计算基本方案的NPV:
NPV 2000( P / F ,10%,1) 1000( P / F ,10%,2) 400( P / F ,10%,3) 600( P / F ,10%,4) 1200( P / A,10%,4)(P / F ,10%,4) 664万元
-5%
0%
5%
10%
15%
20%
1193 -717 1383 971
1060 -372 1203 890
928 -27 1023 812
796 319 844 736
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单因素敏感性分析案例
设有一项目的基本数据如表12—1所示,试对其进行敏感性分析。
解:首先,设定分析的指标为项目财务净现值。
其次,根据有关资料和经验,本项目选销售收入、经营成本和项目总投资三者为不确定因素。
然后,设定不确定因素的变化幅度为%10±,分别计算由此而引致的项目净现值数值及其变化率(分别见表12—2,12—3,12—4),并编制敏感性分析汇总表(见表12—5)
接着,根据上表资料绘制敏感性分析图(见图12—3)
最后,从表和图中均可看出,该项目不确定因素中,销售收入为最敏感性因素。
当销售收入减少%4.12 (即最大极限值)时,项目财务净现值达到零的临界点;经营成本为次敏感性因素;项目总投资的敏感性相对来说较小。
此处的最大极限值可以通过作图法近似地求得,也可通过计算较精确地求得。
设销售收入的极限值为x ,则从上图两三角形相似可得,4.320/8.62/)10(=-x x ,解之即得
%4.12=x 。
多方案比选时,在其它条件相同的情况下,应选择敏感性最小的方案。
表12—3 敏感性分析表:经营成本变化引致项目净现值的变化
表12—5 敏感性分析汇总表 单位:净现值万元,变化率为% 06.810
6
.80==
β。
