例题解答与作业
第三章 PLC例题作业解答
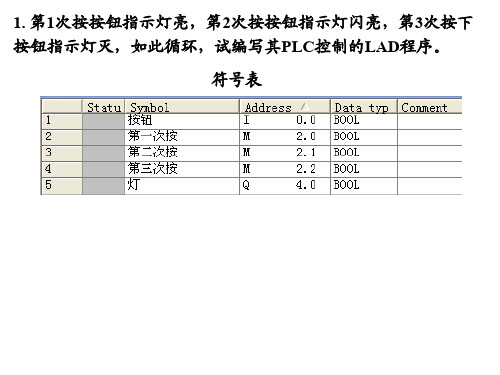
1. 第1次按按钮指示灯亮,第2次按按钮指示灯闪亮,第3次按下 按钮指示灯灭,如此循环,试编写其PLC控制的LAD程序。 符号表
2. 用一个按钮控制2盏灯,第1次按下时第1盏灯亮,第2盏灯灭; 第2次按下时第1盏灯灭,第2盏灯亮;第3次按下时2盏灯都灭。
3. 编写PLC控制程序,使Q4.0输出周期为5s,。鼓风机系统一般有引风机和鼓风 机两级构成。要求: (1).按下起动按钮后首先起动引风机,引风机指示灯亮, 10s后鼓风机自动起动,鼓风机指示灯亮;按下停止按钮后首先 关断鼓风机,鼓风机指示灯灭,经20s后自动关断引风机和引风 机指示灯。 (2).起动按钮接I0.0,停止按钮接I0.1。鼓风机及其指示由 Q4.1和Q4.2驱动,引风机及其指示由Q4.3和Q4.4驱动。
符号表
5. 某设备有3台风机,当设备处于运行状态时,如果有2台或2 台以上风机工作,则指示灯常亮,指示“正常”;如果仅有1台 风机工作,则该指示灯以0.5Hz的频率闪烁,指示“一级报警”; 如果没有风机工作了,则指示灯以2Hz的频率闪烁,指示“严重 警报”。当设备不运转时,指示灯不亮。试用STL及LAD编写符 合要求的控制程序。 提示:本题要点是如何实现“一灯多用”功能。指示灯指示 了4种状态:“正常、一级报警、严重警报、设备停止”。
建筑结构作业解答

1.已知某矩形截面梁b ×h =250 mm ×500mm ,由荷载产生的弯矩设计值M =88.13kN·m,混凝土强度等级为C20,钢筋采用HRB335级, 试求所需纵向受拉钢筋截面面积A s 。
解:查表得:f c =9.6N/mm2,f t =1.1N/mm2,; f y =300N/mm2;ξb =0.55;截面有效高度h 。
=500-40=460mm1.直接公式求解X 根据基本公式可推导出求解X 的公式如下:2.计算受拉钢筋面积 将x 代入下式,受拉钢筋的截面面积为:3.验算条件最小配筋率经过计算比较取ρ min =0.2%A S=704mm2 由以上验算,截面符合适要求。
4.选配钢筋选用2Φ18+1Φ16(A s=710mm2) 一排钢筋所需要的最小宽度为: b min =4×25+2×18+1×16=152mm <250mmmm 25346055.0mm 882506.90.188130000246046020b 2c 1200=⨯=<=⨯⨯⨯--=--=h bf Mh h x ξα2yc 1s mm 704300882506.90.1=⨯⨯⨯==f bxf A α<=⨯⨯=ρ2minmm 250500250002.0bh2.某钢筋混凝土矩形截面简支梁,跨中弯矩设计值M=80kN·m,梁的截面尺寸b×h=200×450mm,采用C25级混凝土,HRB400级钢筋。
试确定跨中截面纵向受力钢筋的数量。
【解】查表得f c=11.9 N/mm2,f t=1.27 N/mm2,f y=360 N/mm2,α1=1.0,ξb=0.5181.确定截面有效高度h0假设纵向受力钢筋为单层,则h0=h-35=450-35=415mm2.计算x,并判断是否为超筋梁==91.0mm<=0.518×415=215.0mm不属超筋梁。
材料科学基础第1-2章例题、作业题及其解答

第2章 例 题(A )1. 在面心立方晶胞中画出[012]和[123]晶向。
2. 在面心立方晶胞中画出(012)和(123)晶面。
3. 右图中所画晶面的晶面指数是多少?4. 设晶面(152)和(034)属六方晶系的正交坐标表述,试给出其四轴坐标的表示。
反之,求(3121)及(2112)的正交坐标的表示。
5. (练习),上题中均改为相应晶向指数,求相互转换后结果。
答案:2. (2110) 4. (1562), (0334) 5. [1322] [1214] (123) (212)[033] [302]第2章 例题答案(A)4. (152) )2615(6)51()(⇒-=+-=+-=v u t(034) )4303(3)30()(⇒-=+-=+-=v u t(1213) ⇒ (123)(2112) ⇒ (212)5. [152] ]2231[22)51(31)(313)152(31)2(311)512(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u [034] ]4121[41)30(31)(312)032(31)2(311)302(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u]3121[]033[33)1(20)1(1⇒⎪⎭⎪⎬⎫===--=-==---=-=w W t v V t u U [2112]]302[20)1(13)1(2⇒⎪⎭⎪⎬⎫===---=-==--=-=w W t v V t u U第2章 例 题(B )1. 已知Cu 的原子直径为2.56A ,求Cu 的晶格常数,并计算1mm 3Cu 的原子数。
2. 已知Al 相对原子质量Ar (Al )=26.97,原子半径γ=0.143nm ,求Al 晶体的密度。
3. bcc 铁的单位晶胞体积,在912℃时是0.02464nm 3;fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。
平移典型例题及练习含答案

平移一、知识点复习知识点1:平移的定义:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
知识点2:平移的要素1.平移的方向:原图上的点指向它的对应点的射线方向;2.平移的距离:连接原图与平移后图形上的一对对应点的线段的长度。
知识点3:平移的性质1.性质(1)平移只改变图形的位置,不改变图形的形状和大小。
(2)平移后的图形与原图形上对应点连成的线段,①数量关系是相等 .②位置关系是平行或在同一条直线上。
2.判断一组图形能不能通过平移得到的方法(1)看对应点连线是否平行或在同一条直线上;(2)看它的形状、大小是否发生变化,位置的变化是否由平移产生。
★★★特别注意:平移是由平移的方向和距离决定的,平移必须指明平移的方向和距离;平移是在平面内,整个图形沿着某一直线平行移动的过程,原图上的每个点都沿同一方向移动相同的距离;平移的距离不能为0;平移的方向是任意的,但就一次平移而言,只能有一个方向,一次平移完成后可以改变方向进行下一次平移。
二、典型例题题型1:生活中平移现象【例题1】(2017春•乌海期末)下列运动属于平移的是()A.荡秋千 B.推开教室的门 C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动【例题2】:(2016春•淮安期中)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是()A.①② B.①③ C.②③ D.③④题型2:平移的性质【例题4】:(2016春•沧州期末)在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC 在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应边中点所连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有()A.①②③④ B.①②③④⑤ C.①②③⑤ D.①③④⑤题型3:与平移有关的计算【例题5】:(2015春•石家庄期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A.2 B.4 C.8 D.16【例题6】:(2017秋•兴化市期末)如图,将△ABE向右平移2cm得到△DCF,AE、DC交于点G.如果△ABE 的周长是16cm,那么△ADG与△CEG的周长之和是 cm。
小学数学 环形跑道问题教案 例题+练习+作业 带答案

环形跑到问题1、知识点总结(1)环形跑道问题同一地点出发,如果是相向而行,则每合走一圈相遇一次(2)环形跑道问题同一地点出发,如果是同向而行,则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题【例题1】一个圆形操场跑道的周长是500米,两个学生同时同地背向而行.黄莺每分钟走66米,麻雀每分钟走59米.经过几分钟才能相遇?黄莺和麻雀每分钟共行66+59=125(千米),那么周长跑道里有几个125米,就需要几分钟,即500÷(66+59)=4(分钟).【巩固】小张和小王各以一定速度,在周长为500米的环形跑道上跑步.小王的速度是200米/分.⑴小张和小王同时从同一地点出发,反向跑步,1分钟后两人第一次相遇,小张的速度是多少米/分?⑵小张和小王同时从同一点出发,同一方向跑步,小张跑多少圈后才能第一次追上小王?⑴两人相遇,也就是合起来跑了一个周长的行程.小张的速度是500÷1-200=300(米/分).⑵在环形的跑道上,小张要追上小王,就是小张比小王多跑一圈(一个周长),因此需要的时间是:500÷(300-200)=5(分).300×5÷500=3(圈).【例题2】上海小学有一长300米长的环形跑道,小亚和小胖同时从起跑线起跑,小亚每秒钟跑6米,小胖每秒钟跑4米,(1)小亚第一次追上小胖时两人各跑了多少米?(2)小亚第二次追上小胖两人各跑了多少圈?第一次追上时,小亚多跑了一圈,所以需要300÷(6-4)=150秒,小亚跑了6×150=900(米)。
小胖跑了4×150=600(米);第一次追上时,小胖跑了2圈,小亚跑了3圈,所以第二次追上时,小胖跑4圈,小亚跑6圈。
【巩固】一条环形跑道长400米,甲骑自行车每分钟骑450米,乙跑步每分钟250米,两人同时从同地同向出发,经过多少分钟两人相遇?400÷(450-250)=2(分钟).【例题3】在300米的环形跑道上,田奇和王强同学同时同地起跑,如果同向而跑2分30秒相遇,如果背向而跑则半分钟相遇,求两人的速度各是多少?同向而跑,这实质是快追慢.起跑后,由于两人速度的差异,造成两人路程上的差异,随着时间的增长,两人间的距离不断拉大,到两人相距环形跑道的半圈时,相距最大.接着,两人的距离又逐渐缩小,直到快的追上慢的,此时快的比慢的多跑了一圈.背向而跑即所谓的相遇问题,数量关系为:路程和÷速度和=相遇时间.同向而行2分30秒相遇,2分30秒=150秒,两个人的速度和为:300÷150=2(米/秒),背向而跑则半分钟即30秒相遇,所以两个人的速度差为:300÷30=10(米/秒).两人的速度分别为:(10-2)÷2=4(米/秒), 10-4=6(米/秒)【巩固】在400米的环形跑道上,甲、乙两人同时同地起跑,如果同向而行3分20秒相遇,如果背向而行40秒相遇,已知甲比乙快,求甲、乙的速度各是多少?甲乙的速度和为:400÷40=10(米/秒),甲乙的速度差为:400÷200=2(米/秒),甲的速度为:(10+2)÷2=6(米/秒),乙的速度为:(10-2)÷2=4(米/秒).【例题4】两人在环形跑道上跑步,两人从同一地点出发,小明每秒跑3米,小雅每秒跑4米,反向而行,45秒后两人相遇。
趋势预测法例题参考及作业

例题1:某公司近五年的销售额数据如下:年份 | 销售额(万元)|2018 | 5002019 | 5502020 | 6002021 | 6502022 | 700解答思路:1. 计算销售额的平均增长率:计算每年的销售额增长量,然后求出这五年销售额增长量的平均值,即为平均增长率。
2. 预测2023年的销售额:根据平均增长率,计算2023年的销售额。
作业1:某学校近五年的学生人数数据如下:年份 | 学生人数|2018 | 10002019 | 10502020 | 11002021 | 11502022 | 1200例题2:某城市近五年的房价数据如下:年份 | 房价(元/平方米)|2018 | 100002019 | 110002020 | 120002021 | 130002022 | 14000解答思路:1. 计算房价的平均增长率:计算每年的房价增长量,然后求出这五年房价增长量的平均值,即为平均增长率。
2. 预测2023年的房价:根据平均增长率,计算2023年的房价。
作业2:某地区的居民收入数据如下:年份 | 居民收入(元/人)|2018 | 200002019 | 210002020 | 220002021 | 230002022 | 24000例题3:某电商平台的月销售额数据如下:月份 | 销售额(万元)|1月 | 3002月 | 3203月 | 3404月 | 3605月 | 380解答思路:1. 计算销售额的平均增长率:计算每个月的销售额增长量,然后求出这五个月销售额增长量的平均值,即为平均增长率。
2. 预测6月的销售额:根据平均增长率,计算6月的销售额。
作业3:某超市的月销售量数据如下:月份 | 销售量(件)|1月 | 10002月 | 11003月 | 12004月 | 13005月 | 1400。
平面直角坐标系典型例题含答案及解析

平面直角坐标系一、知识点复习1.有序数对:有顺序的两个数a 与b 组成的数对,记作),(b a 。
注意a 与b 的先后顺序对位置的影响。
2.平面直角坐标系(1)定义:在同一平面内画两条相互垂直并且原点重合的数轴,组成平面直角坐标系。
这个平面叫做坐标平面。
(2)平面直角坐标系中点的坐标:通常若平面直角坐标系中有一点A ,过点A 作横轴的垂线,垂足在横轴上的坐标为a ,过点A 作纵轴的垂线,垂足在纵轴上的坐标为b ,有序实数对),(b a 叫做点A 的坐标,其中a 叫横坐标,b 叫做纵坐标。
3.各象限内的点与坐标轴上的点的坐标特征:4. 特殊位置点的特殊坐标5.对称点的坐标特征:6.点到坐标轴的距离:点)P到X轴距离为y,到y轴的距离为x。
x,(y7.点的平移坐标变化规律:简单记为“左减右加,上加下减”二、典型例题讲解考点1:点的坐标与象限的关系1.在平面直角坐标系中,点P (-2,3)在第( )象限. A .一 B .二 C .三 D .四2.若点)2,(-a a P 在第四象限,则a 的取值范围是( )A. 02<<-aB.20<<aC.2>aD.0<a 3.在平面直角坐标系中,点P (-2,12+x )所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 考点2:点在坐标轴上的特点1.点)1,3(++m m P 在x 轴上,则P 点坐标为( ) A .)2,0(- B.)0,2( C.)0,4( D.)4,0(-2.已知点)12,(-m m P 在y 轴上,则P 点的坐标是 。
3.若点P (x ,y )的坐标满足xy=0(x ≠y ),则点P 必在( ) A .原点上 B .x 轴上 C .y 轴上 D .x 轴上或y 轴上(除原点) 考点3:对称点的坐标1.平面直角坐标系中,与点)3,2(-关于原点中心对称的点是( ) A.)2,3(- B.)2,3(- C.)3,2(- D.(2,3)2.已知点A 的坐标为(-2,3),点B 与点A 关于x 轴对称,点C 与点B 关于y 轴对称,则点C 关于x 轴对称的点的坐标为( )A .(2,-3)B .(-2,3)C .(2,3)D .(-2,-3) 3.若坐标平面上点P (a ,1)与点Q (-4,b )关于x 轴对称,则( ) A .a=4,b=-1 B .a=-4,b=1 C .a=-4,b=-1 D .a=4,b=1 考点4:点的平移1.已知点A (-2,4),将点A 往上平移2个单位长度,再往左平移3个单位长度得到点A ′,则点A ′的坐标是( )A .(-5,6)B .(1,2)C .(1,6)D .(-5,2)2.已知A (2,3),其关于x 轴的对称点是B ,B 关于y 轴对称点是C ,那么相当于将A 经过( )的平移到了C .A .向左平移4个单位,再向上平移6个单位B .向左平移4个单位,再向下平移6个单位C .向右平移4个单位,再向上平移6个单位D .向下平移6个单位,再向右平移4个单位3.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2 B.3 C.4 D.5考点5:点到坐标轴的距离考点6:平行于x轴或y轴的直线的特点1.如图,AD∥BC∥x轴,下列说法正确的是()A.A与D的横坐标相同 B.C与D的横坐标相同C.B与C的纵坐标相同 D.B与D的纵坐标相同2.已知点A(m+1,-2)和点B(3,m-1),若直线AB∥x轴,则m的值为()A.2 B.-4 C.-1 D.33.已知点M(-2,3),线段MN=3,且MN∥y轴,则点N的坐标是()A.(-2,0) B.(1,3)C.(1,3)或(-5,3) D.(-2,0)或(-2,6)考点7:角平分线的理解1.已知点A(3a+5,a-3)在二、四象限的角平分线上,则a= .考点8:特定条件下点的坐标1.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为()A.(3,2)B.(3,1)C.(2,2)D.(﹣2,2)考点9:面积的求法(割补法)1.(1)在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3);( 2)顺次连接A,B,C,组成△ABC,求△ABC的面积.参考答案:(1)略(2)8.52.如图,在四边形ABCD中,A、B、C、D的四个点的坐标分别为(0,2)(1,0)(6,2)(2,4),求四边形ABCD的面积.3.在图中A(2,-4)、B(4,-3)、C(5,0),求四边形ABCO的面积.考点10:根据坐标或面积的特点求未知点的坐标1.已知A (a ,0)和B 点(0,10)两点,且AB 与坐标轴围成的三角形的面积等于20,则a 的值为( )A .2B .4C .0或4D .4或-4 2.如图,已知:)4,5(-A 、)2,2(--B 、)2,0(C 。
五上数学小数除法应用题训练 例题+课后作业

五年级上学期小数除法应用题题型训练知识点总结:1、进一法:将结果中小数部分舍去,向各位进一2、去尾法:将结果中小数部分舍去3、注意:根据实际情况会用“进一法”或“去尾法”取商的近似数例题讲解:例1、平均数问题(1)张爷爷跑2.5千米用20分钟,他平均跑1千米需要()分钟,平均每分钟跑()千米。
(2)幼儿园把 1.25 千克的糖果平均分给 5 个小朋友,每小朋友分得()千克。
(3)一辆汽车 2.4 小时行驶 60 千米,1 小时行驶()千米,行驶 1 千米需要()小时。
(4)一台拖拉机 0.75 小时耕地 60 公顷,1 小时耕地()公顷,耕 1 公顷地需要()小时。
演练1、练一练(1)5吨菜籽可以榨油 4 吨,榨 1 吨油需要()吨菜籽,每吨菜籽可以榨()吨油。
(2)一群小朋友去游乐场玩,他们玩激流勇进一共花了52.5元,玩碰碰车一共花了79.5元。
激流勇进每人3.5元,碰碰车每人多少钱?例2、货币兑换问题2018年2月27日,中国银行外汇牌价如下图,在这一天里:(1)100元人民币可以兑换多少港币?(保留两位小数)(2)一个书包标价3.9美元,100元人民币可以买几个?演练2、货币兑换问题下面是2018年2月5日的中国银行外汇牌价。
(单位:元)在这一天里:(1)200元人民币可以兑换多少美元?(结果保留两位小数)(2)同一款苹果手机在英国标价510英镑,在香港标价5288港元。
哪儿的标价低?(3)一个文具盒标价3.4美元,用100元人民币可以买几个?例3、分段计费问题王阿姨给在外省读大学的女儿寄衣服,衣服重26kg,需要付多少元快递费?演练3、分段计费问题为了鼓励市民节约用电,某市电力公司规定了以下的电费计算办法。
李阿姨家十一月份缴电费61.6元,她家十一月份用电多少千瓦时?例4、比一比打电话时,国内长途每分钟0.7元,国际长途每小时7.2元,小明打国际长途用了27.36元,小丽打国内长途用了6.86元,算一算,他们谁打电话的时间长一些。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:某电路各级均为共射放大电路,其对数幅频特性如图所示。
求下
限频率、上限频率和电压放大倍数。
解:(1)低频段只有一个拐点,说明影响低频特性的只有一个电容,
故电路的下限频率为10Hz 。
2)高频段只有一个拐点,斜率为-60dB/十倍频程,电路中应有三
个电容,为三级放大电路。
f H ≈0.52f H1=(0.52×2×105)Hz=104KHz
3)电压放大倍数:
作业:
已知某放大电路的幅频特性如图所示,讨论下列问题:
1. 该放大电路为几级放大电路?
2. 耦合方式?
3. 在 f =104Hz 时,增益下降多少?附加相移φ’=?
4. 在 f =105Hz 时,附加相移φ’≈?
5. 画出相频特性曲线; 354)10
21)(101(10⨯++-=∙f j jf A u
6. f H=?Au表达式?。
