(完整版)专题:反比例函数与相似综合
中考反比例函数与几何综合
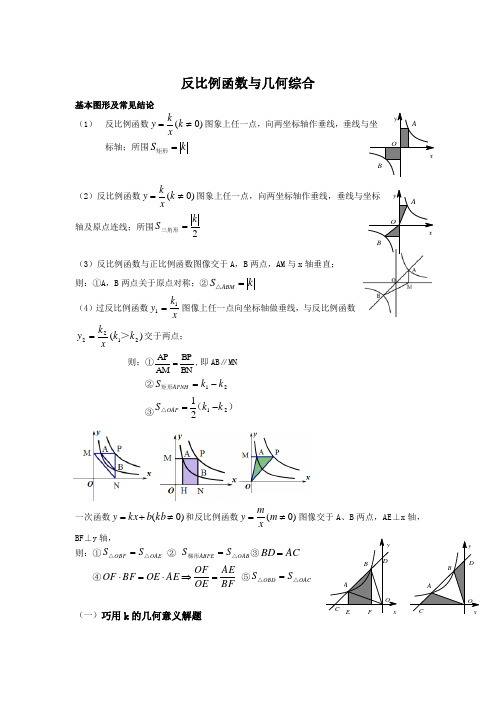
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 (1) 反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴;所围k S =矩形(2)反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴及原点连线;所围2k S =三角形(3)反比例函数与正比例函数图像交于A ,B 两点,AM 与x 轴垂直; 则:①A ,B 两点关于原点对称;②k S ABM =△(4)过反比例函数xk y 11=图像上任一点向坐标轴做垂线,与反比例函数)(2122k k xk y >=交于两点; 则:①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③)(△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点,AE ⊥x 轴,BF ⊥y 轴,则:①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=(一)巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1.函数y=和y=在第一象限内的图象如图,点P 是y=的图象上一动点,PC ⊥x 轴于点C ,交y=的图象于点B .给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=AP .其中所有正确结论的序号是________。
迁移练习1(1).如图,双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ,与AB 交于点C .若△OBC 面积为3,则k =_______迁移练习1(2)..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ,交BC 于点E ; 若梯形OEBA 的面积为9,则k=________。
(完整版)初中数学反比例函数知识点及经典例

04
利用相似三角形求解线段长度或角度大小
通过相似三角形的性质,我们可以建立 比例关系,从而求解未知线段长度或角 度大小。
解方程求解未知量。
具体步骤
根据相似比建立等式关系。
确定相似三角形,找出对应边或对应角 。
经典例题讲解和思路拓展
例题1
解题思路
例题2
解题思路
已知直角三角形ABC中, ∠C=90°,AC=3,BC=4,将 △ABC沿CB方向平移2个单位 得到△DEF,若AG⊥DE于点G ,则AG的长为____反比例函数$y = frac{m}{x}$的图像经过点$A(2,3)$,且与直线$y = -x + b$相 交于点$P(4,n)$,求$m,n,b$的
值。
XXX
PART 03
反比例函数与不等式关系 探讨
REPORTING
一元一次不等式解法回顾
一元一次不等式的定义
01
在材料力学中,胡克定律指出弹簧的 伸长量与作用力成反比。这种关系同 样可以用反比例函数来描述。
牛顿第二定律
在物理学中,牛顿第二定律表明物体 的加速度与作用力成正比,与物体质 量成反比。这种关系也可以用反比例 函数来表示。
经济学和金融学领域应用案例分享
供需关系
在经济学中,供需关系是决定商品价 格的重要因素。当供应量增加时,商 品价格下降;反之,供应量减少时, 商品价格上升。这种供需关系可以用 反比例函数来表示。
XXX
PART 02
反比例函数与直线交点问 题
REPORTING
求解交点坐标方法
方程组法
将反比例函数和直线的方程联立 ,解方程组得到交点坐标。
图像法
在同一坐标系中分别作出反比例 函数和直线的图像,找出交点并 确定其坐标。
反比例函数的图像和性质的综合应用

解析
根据题意,将点 A(-2 ,3)和点 B(3,-2 )分别代入两个函数中 ,得到关于 m、k、b 的方程组,解方程组求 得 m、k、b 的值,即 可得到两个函数的解析
式。
05
反比例函数在几何图形中应用
相似三角形判定定理推广
预备定理
平行于三角形的一边,并且和 其他两边相交的线段,所截得 的三角形的三边与原三角形三 边对应成比例。
反比例函数图像在平面直角坐标系中 ,沿y轴方向平移,函数表达式不变, 图像沿y轴平移。
伸缩变换规律
01
当k>0时,图像分别位于第一、三象限,每一个象限内,从 左往右,y随x的增大而减小;
02
当k<0时,图像分别位于第二、四象限,每一个象限内,从 左往右,y随x的增大而增大。
03
k>0时,函数在x<0上同为减函数、在x>0上同为减函数; k<0时,函数在x<0上为增函数、在x>0上同为增函数。
3
平行四边形面积问题
通过已知相邻两边及其夹角求解面积,或已知面 积和一边长度及夹角求解另一边长度,应用反比 例函数进行求解。
速度、时间、距离关系分析
匀速直线运动问题
通过已知速度和时间求解距离,或已 知距离和时间求解速度,利用反比例 关系建立方程。
变速直线运动问题
曲线运动问题
通过已知速度和方向的变化规律,求 解某时刻的速度或某段时间内的平均 速度及运动轨迹,结合反比例函数进 行综合分析。
解析
根据题意,将点(-2, -1)代入两个函数中, 得到关于 k、m、n 的 方程组,解方程组求得 k、m、n 的值,即可 得到两个函数的解析式 。再将 x = 3 代入两个 函数中,得到关于 k、 m、n 的另一个方程, 与前面的方程组联立求 解,即可得到最终的解
反比例函数复习课完整版课件

通过观察反比例函数和直线图像的相对位置关系,可以直观判断交点的存在性及 个数。例如,当直线与双曲线有两个交点时,说明存在两个解;当直线与双曲线 相切时,说明存在一个解;当直线与双曲线无交点时,说明不存在解。
03 反比例函数在实际问题中 应用
生活中常见问题建模为反比例关系
路程、速度和时间的关系
当路程一定时,速度和时间成反比例关系。例如,从家到学校距离一定,步行速度越快, 所需时间越短。
工作总量、工作效率和工作时间的关系
当工作总量一定时,工作效率和工作时间成反比例关系。例如,完成一项任务所需的总工 作量是固定的,工作效率越高,所需时间越短。
矩形面积、长和宽的关系
当矩形面积一定时,长和宽成反比例关系。例如,一块固定面积的土地,长度越长,宽度 就越短。
我们探讨了反比例函数与直线交点的求解方法,以及交点存在
和不存在的条件。
学生自我评价报告分享
01
02
03
知识掌握情况
学生们表示通过本节课的 复习,对反比例函数的概 念、性质和应用有了更深 刻的理解。
学习方法反思
部分学生提到,在解决反 比例函数与直线交点问题 时,需要更加细心地处理 计算过程,以避免出错。
反比例函数定义
形如 $y = frac{k}{x}$ (其中 $k$ 为常 数,且 $k neq 0$) 的函数称为反比 例函数。
反比例函数表达式
比例系数的意义
$k$ 决定了反比例函数的图像和性质 ,当 $k > 0$ 时,图像位于第一、三 象限;当 $k < 0$ 时,图像位于第二 、四象限。
$y = frac{k}{x}$,其中 $x$ 是自变量 ,$y$ 是因变量,$k$ 是比例系数。
专题九-反比例函数与几何的综合应用

在物理学中,一些物理量之间可能存在反比例关系,如电阻与电流、压力与面积等。通过运用反 比例函数的性质,可以更好地理解和解决这些物理问题。
反比例函数在经济学中的应用
在经济学中,一些经济指标之间可能存在反比例关系,如价格与需求量、成本与产量等。通过运 用反比例函数的性质,可以对这些经济指标进行更准确的预测和分析。
如长度、面积等。
利用反比例函数性质建立关系
02
根据反比例函数的性质,结合几何图形的特点,建立所求最值
与相关量之间的关系。
求解最值
03
通过求解反比例函数的最值,得到所求几何量的最值。
判定存在性问题
根据题意列出方程或不等式
01
根据题目条件,列出与几何图形相关的方程或不等式
。
利用反比例函数性质分析解的情况
反比例关系在圆中的应用
在圆中,当一个圆的半径增加时,其 面积会按平方比例增加,但其周长只 会按线性比例增加。这种关系虽然不 是严格的反比例关系,但也可以用于 解决一些与圆相关的问题。
解题技巧与实例分析
通过利用圆的性质和上述关系, 可以求解一些与圆相关的问题。 例如,已知一个圆的半径和另一 个圆的面积或周长,可以求解未 知圆的半径或面积等。
仔细阅读题目要求,明确题意 ,避免答非所问。
合理安排答题顺序
先做易做的题目,确保会做的 题目不丢分,再攻克难题。
控制答题时间
每道题目分配合理的时间,避 免时间不够用或浪费过多时间
。
检查答案
做完题目后要认真检查答案, 确保没有遗漏或错误。
THANKS FOR WATCHING
感谢您的观看
解题技巧与实例分析
对于其他几何图形中的反比例关系问题,可以通过设定未知数、利用几何图形的性质和反比例关系来求解。 需要注意的是,在解题过程中要仔细分析题目条件和数据特点,选择合适的解题方法和思路。
反比例函数与相似
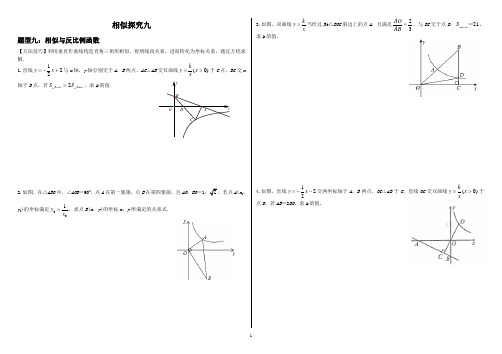
xy DB AOC相似探究九题型九:相似与反比例函数【方法技巧】利用垂直作垂线构造直角三角形相似,得到线段关系,进而转化为坐标关系,通过方程求解. 1.直线122y x =-+与x 轴,y 轴分别交于A ,B 两点,AC ⊥AB 交双曲线(0)ky x x=>于C 点,BC 交x 轴于D 点,若2ACDABD SS=,求k 的值.2.如图,在△ABO 中,∠AOB =900,点A 在第一象限,点B 在第四象限,且AO :BO =12A (x 0,y 0)的坐标满足001y x =,求点B (x ,y )的坐标x ,y 所满足的关系式.3.如图,双曲线k y x =当经过Rt △BOC 斜边上的点A ,且满足23AO AB =,与BC 交于点D ,21BODS =,求k 的值,4.如图,直线122y x =--交两坐标轴于A ,B 两点,OC ⊥AB 于C ,直线OC 交双曲线(0)ky x x=>于点D ,若AB =2DO ,求k 的值.相似探究(十)题型十:相似与反比例函数【方法技巧】利用垂直作垂线构造直角三角形相似,将线段关系转化为坐标关系,通过方程求解. 1.如图,直线y =kx (k >0)分别交双曲线y =2x (x >0)和双曲线y =4x (x >0)于A ,B 两点,求OAOB的值.2.如图,在AOB 中,AOB =90,点A 在双曲线y =()0k x x <上,点B 在双曲线y =1x(x >0)上. (1)若k =-2,求OAOB的值; (2)若∠OAB =30°,求k 的值.3.如图,点A 是双曲线y =2x在第一象限的分支上的一个动点,连接AO 并延长交另一分支于 点B ,以AB 为边作等边ABC ,点C 在第四象限,随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线y =kx(X >0)上运动,求k 的值.。
(完整版)专题:反比例函数与相似综合

中考数学专题复习:反比例函数与相似的综合题【考点分析】近几年的中考数学题中,对于反比例函数与几何图形的结合的考查力度明显加大,主要考查:①平面直角坐标系中,如何把线段转化为坐标,坐标转化为含有字母的代数式, 进而进行代数计算;②反比例函数与相似图形的综合题;③反比例函数与几何图形的平移。
【专题攻略】在平面直角坐标系中,反比例函数与几何图形的综合题,最基本的解决方法是:由点的坐标求相关线段的长度,根据相关线段的长度表示点的坐标。
这类题在解答时要求我们要熟练运用数学基础知识,还要能灵活运用数形结合、转化、待定系数、分类讨论等基本数学思想和方法。
【课前训练】k1、如图,面积为3的矩形OABC勺一个顶点B在反比例函数y 的图象上,另三点在坐x标轴上,则k= .交于点0若厶OBA的面积为6,则k =k4、如图,已知双曲线y -(k>0)经过直角三角形OAB斜边X交于点0若厶OBC勺面积为3,贝y k = ______________3、如图,已知双曲线第3、4题X轴于B点,若S A AOB = 3,则k =ky (k>0)经过直角三角形OAB斜边xOB的中点D,与直角边AB相OB的中点D,与直角边AB相【典型例题】(2010年广州中考第23题)已知反比例函数y= m__ (m为常数)的图象经过点A (- 1, 6).x(1)求m的值;(2)如图9,过点与x轴交于点C,(2014南沙区一模)如图,已知直线y 4 x与反比例函数y m m>0, x > 0的图象x交于A、B两点,与x轴、y轴分别相交于C、D两点.(1)若点A的横坐标为1,求m的值并利用函数图象求关于x的不等式4 x< m的解集;x(2)是否存在以AB为直径的圆经过点P(1,0)?若存在,求出m的值;若不存在,请说明理由.1、( 2013?宁波)如图,等腰直角三角形 / BCA=90 ° AC=BC=2 典,反比例函数与AB , BC 交于点D , E .连结。
初中数学中考复习 备战2020年中考数学一轮专项复习——反比例函数综合问题(含详细解答)

备战2020年中考数学一轮专项复习——反比例函数综合问题一、反比例函数的概念:知识要点:1、一般地,形如 y = x k ( k 是常数, k = 0 ) 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;(2)解析式有三种常见的表达形式:(A )y = xk (k ≠ 0) ; (B )xy = k (k ≠ 0); (C )y=kx -1(k ≠0) 二、反比例函数的图象和性质:知识要点:1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第一、三象限内;(2)当k<0时, 双曲线分别位于第二、四象限内。
3、增减性:(1)当k>0时,y = xk (k ≠ 0)为减函数,y 随x 的增大而减小; (2)当k<0时,y = xk (k ≠ 0)为增函数,y 随x 的增大而增大。
4、变化趋势:双曲线无限接近于x 、y 轴,但永远不会与坐标轴相交5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点成中心对称;(2)对于k 取互为相反数的两个反比例函数(如:y =x 6 和y = x 6 )来说,它们是关于x 轴,y 轴成轴对称。
一、选择题:1.下列函数,①y =2x ,②y =x ,③y =x ﹣1,④y =是反比例函数的个数有( ) A .0个 B .1个 C .2个 D .3个【分析】根据反比例函数的定义,反比例函数的一般式是(k ≠0)判定则可. 【解析】①y =2x 是正比例函数;②y =x 是正比例函数;③y =x ﹣1是反比例函数;④y=不是反比例函数,是反比例关系;所以共有1个.故选:B.2.(2019•济南)函数y=﹣ax+a与y=(a≠0)在同一坐标系中的图象可能是()A.B.C.D.【解析】a>0时,﹣a<0,y=﹣ax+a在一、二、四象限,y=在一、三象限,无选项符合.a<0时,﹣a>0,y=﹣ax+a在一、三、四象限,y=(a≠0)在二、四象限,只有D符合;故选:D.3.如图,过原点的直线l与反比例函数y=﹣的图象交于M,N两点,根据图象猜想线段MN的长的最小值是()A.B.2C.2 D.1【分析】设N的横坐标是a,则纵坐标是﹣,利用a即可表示出ON的长度,然后根据不等式的性质即可求解.【解析】设N的横坐标是a,则纵坐标是﹣.则OM=ON=≥.则MN的最小值是2.故选:B.4.(2019•阜新)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y 轴上,则△ABC的面积为()A.3 B.2 C.D.1【解析】连结OA,如图,∵AB⊥x轴,∴OC∥AB,∴S△OAB=S△CAB,而S△OAB=|k|=,∴S△CAB=,故选:C.5.(2019•遵义)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为()A.2 B.3 C.4 D.6【解析】过点A作x轴的垂线,交CB的延长线于点E,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为4,2,∴A(,4),B(,2),∴AE=2,BE=k﹣k=k,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE==1∴k=1,∴k=4.故选:C.6.如图,在菱形ABOC中,∠ABO=120°,它的一个顶点C在反比例函数y=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则该反比函数的表达式为()A.y=﹣B.y=﹣C.y=﹣D.y=﹣【分析】点C作CD⊥x轴于D,设菱形的边长为a,根据菱形的性质和三角函数分别表示出C,以及点A向下平移2个单位的点,再根据反比例函数图象上点的坐标特征得到方程组求解即可.【解析】过点C作CD⊥x轴于D,设菱形的边长为a,在Rt△CDO中,OD=a•cos60°=a,CD=a•sin60°=a,则C(﹣a,a),点A向下平移2个单位的点为(﹣a﹣a,a﹣2),即(﹣a,a﹣2),则,解得.故反比例函数解析式为y=﹣.故选:B.7.(2019•淄博)如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x 轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数y =(x>0)的图象上.则y1+y2+…+y10的值为()A.2B.6 C.4D.2【解析】过C1、C2、C3…分别作x轴的垂线,垂足分别为D1、D2、D3…其斜边的中点C1在反比例函数y=,∴C(2,2)即y1=2,∴OD1=D1A1=2,设A1D2=a,则C2D2=a此时C2(4+a,a),代入y=得:a(4+a)=4,解得:a=,即:y2=,同理:y3=,y 4=,……∴y1+y2+…+y10=2+++……=,故选:A.8.如图,已知点A,B在双曲线y=(x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P 是AC的中点.若△ABP的面积为4,则k的值为().A.16 B.8 C.4 D.24【分析】由△ABP的面积为4,知BP•AP=8.根据反比例函数y=中k的几何意义,知本题k=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.【解答】解:∵△ABP 的面积为•BP •AP =4,∴BP •AP =8,∵P 是AC 的中点,∴A 点的纵坐标是B 点纵坐标的2倍,又∵点A 、B 都在双曲线y =(x >0)上,∴B 点的横坐标是A 点横坐标的2倍,∴OC =DP =BP ,∴k =OC •AC =BP •2AP =16.故选A.二、填空题:9.(2019山西)如图,在平面直角坐标系中,点O 为坐标原点,菱形ABCD 的顶点B 在x 轴的正半轴上,点A 坐标为(-4,0),点D 的坐标为(-1,4),反比例函数)0(>=x xk y 的图象恰好经过点C ,则k 的值为 .【解析】过点D 作DE ⊥AB 于点E ,则AD=5,∵四边形ABCD 为菱形,∴CD=5∴C (4,4),将C 代入x k y =得:44k =,∴16=k10.(2019遂宁中考 第15题 4分)如图,在平面直角坐标系中,矩形OABC 的顶点O 落在坐标原点,点A 、点C 分别位于x 轴,y 轴的正半轴,G 为线段OA 上一点,将△OCG 沿CG 翻折,O 点恰好落在对角线AC 上的点P 处,反比例函数y =经过点B .二次函数y =ax 2+bx +c (a ≠0)的图象经过C (0,3)、G 、A 三点,则该二次函数的解析式为 .(填一般式)【解析】点C (0,3),反比例函数y =经过点B ,则点B (4,3),则OC =3,OA =4,∴AC =5,设OG =PG =x ,则GA =4﹣x ,PA =AC ﹣CP =AC ﹣OC =5﹣3=2, 由勾股定理得:(4﹣x )2=4+x 2,解得:x =,故点G (,0),将点C 、G 、A 坐标代入二次函数表达式得:,解得:,故答案为:y =x 2﹣x +3. 11.如图,已知点(1,3)在函数y =kx (x >0)的图象上,正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数y =kx(x >0)的图象又经过A ,E 两点,则点E 的横坐标为____.【解析】 把(1,3)代入到y =kx,得k =3, 所以函数解析式为y =3x. 设A (a ,b ),根据图象和题意可知,点E ⎝ ⎛⎭⎪⎫a +b 2,b 2.因为y =3x 的图象经过A ,E ,所以分别把点A 和E 代入到函数解析式中得 ab =3,①b 2⎝ ⎛⎭⎪⎫a +b 2=3,② 由②得ab 2+b 24=3,把①代入得32+b 24=3, 即b 2=6,解得b =±6,因为A 在第一象限,所以b >0,所以b = 6.把b =6代入①求得a =62, 所以点E 的横坐标为a +b 2= 6.故答案为 6. 12.如图,Rt △AOB 中,∠OAB =90°,∠OBA =30°,顶点A 在反比例函数y =图象上,若Rt △AOB 的面积恰好被y 轴平分,则进过点B 的反比例函数的解析式为 .【分析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ),则ab =﹣4.根据两角对应相等的两三角形相似,得出△OAE ∽△ABF ,由相似三角形的对应边成比例,则BD 、OD 都可用含a 、b 的代数式表示,从而求出B 的坐标,进而得出结果.【解析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ).∵顶点A 在反比例函数y =图象上,∴ab=﹣4.∵∠OAB=90°,∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,∴△OAE∽△ABF,∴OA:AB=OE:AF=AE:BF,在Rt△AOB中,∠AOAB=90°,∠OBA=30°,∴OA:AB=1:,∴﹣a:AF=b:BF=1:,∴AF=﹣,BF=b,∵Rt△AOB的面积恰好被y轴平分,∴AC=BC,∴BD=DF=BF=﹣a,OD=AE+AF=b﹣a,∴b=﹣a,∴A(﹣b,b),B(b,b﹣)∴﹣b•b=﹣4,∴b2=,∴k=b(b﹣)=b2﹣ab=10,故答案为:10.13.如图, △OAP ,△ABQ 是等腰直角三角形,点P ,Q 在反比例函数y =4x (x >0)上,直角顶点A ,B 均在x 轴上,则点Q 的坐标为 .【解析】 ∵△OAP 是等腰直角三角形,∴PA =OA .∴设P 点的坐标是(a ,a ),把(a ,a )代入解析式y =4x,解得a =2(a =-2舍去), ∴P 的坐标是(2,2),∴OA =2,∵△ABQ 是等腰直角三角形,∴BQ =AB ,∴可以设Q 的纵坐标是b ,∴横坐标是b +2,把Q 的坐标代入解析式y =4x, 得b =4b +2,∴b =5-1(b =-5-1舍去),∴点Q 的坐标为(5+1,5-1).14.(2019•毕节市)如图,在平面直角坐标中,一次函数y =﹣4x +4的图象与x 轴、y 轴分别交于A 、B 两点.正方形ABCD 的顶点C 、D 在第一象限,顶点D 在反比例函数y =(k ≠0)的图象上.若正方形ABCD 向左平移n 个单位后,顶点C 恰好落在反比例函数的图象上,则n 的值是 .【解析】过点D 作DE ⊥x 轴,过点C 作CF ⊥y 轴,∵AB ⊥AD ,∴∠BAO =∠DAE ,∵AB =AD ,∠BOA =∠DEA ,∴△ABO ≌△DAE (AAS ),∴AE =BO ,DE =OA ,易求A (1,0),B (0,4),∴D (5,1),∵顶点D 在反比例函数y =上,∴k =5,∴y =,易证△CBF ≌△BAO (AAS ),∴CF =4,BF =1,∴C (4,5),∵C 向左移动n 个单位后为(4﹣n ,5),∴5(4﹣n )=5,∴n =3,故答案为3;三、解答题15.如图,一次函数y =kx +2的图象与反比例函数y =m x的图象在第一象限的交点为P .PA 垂直x 轴于点A .PB 垂直y 轴于点B .函数y =kx +2的图象分别交x 轴,y 轴于点C ,D .已知DB =2OD ,△PBD 的面积S △PBD =4.(1)求点D 的坐标;(2)求k ,m 的值;(3)写出当x >0时,使一次函数y =kx +2的值大于反比例函数y =m x的值的x 的取值范围.【解析】(1)在y =kx +2中,令x =0,得y =2,所以点D (0,2).(2)因为OD =2,DB =2OD =4,由S △PBD =4,可得BP =2,而OB =OD +DB =6,所以点P (2,6).将P (2,6)分别代入y =kx +2与y =mx,可得 k =2,m =12.(3) 由图象可知,当x >0时,使一次函数y =kx +2的值大于反比例函数y =mx的值的x 的取值范围是x >2.16.(2019遂宁中考 第23题 10分)如图,一次函数y =x ﹣3的图象与反比例函数y ═(k ≠0)的图象交于点A 与点B (a ,﹣4).(1)求反比例函数的表达式;(2)若动点P 是第一象限内双曲线上的点(不与点A 重合),连接OP ,且过点P 作y 轴的平行线交直线AB于点C,连接OC,若△POC的面积为3,求出点P的坐标.【解析】(1)将B(a,﹣4)代入一次函数y=x﹣3中得:a=﹣1∴B(﹣1,﹣4)将B(﹣1,﹣4)代入反比例函数y═(k≠0)中得:k=4∴反比例函数的表达式为y=;(2)如图:设点P的坐标为(m,)(m>0),则C(m,m﹣3)∴PC=|﹣(m﹣3)|,点O到直线PC的距离为m∴△POC的面积=m×|﹣(m﹣3)|=3解得:m=5或﹣2或1或2∵点P不与点A重合,且A(4,1)∴m≠4又∵m>0∴m=5或1或2∴点P的坐标为(5,)或(1,4)或(2,2).17.(2019•河池)在平面直角坐标系中,矩形ABCD的顶点坐标为A(0,0),B(6,0),C(6,8),D(0,8),AC,BD交于点E.(1)如图(1),双曲线y=过点E,直接写出点E的坐标和双曲线的解析式;(2)如图(2),双曲线y=与BC,CD分别交于点M,N,点C关于MN的对称点C′在y轴上.求证△CMN~△CBD,并求点C′的坐标;(3)如图(3),将矩形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线y=与AD交于点P.当△AEP为等腰三角形时,求m的值.【解析】(1)如图1中,∵四边形ABCD是矩形,∴DE=EB,∵B(6,0),D(0,8),∴E(3,4),∵双曲线y=过点E,∴k1=12.∴反比例函数的解析式为y=.(2)如图2中,∵点M,N在反比例函数的图象上,∴DN•AD=BM•AB,∵BC=AD,AB=CD,∴DN•BC=BM•CD,∴=,∴=,∴=,∵∠MCN=∠BCD,∴△MCN∽△BCD,∴∠CNM=∠CDB,∴MN∥BD,∴△CMN∽△CBD.∵B(6,0),D(0,8),∴直线BD的解析式为y=﹣x+8,∵C,C′关于MN对称,∴CC′⊥MN,∴CC′⊥BD,∵C(6,8),∴直线CC′的解析式为y=x+,∴C′(0,).(3)如图3中,①当AP=AE=5时,∵P(m,5),E(m+3,4),P,E在反比例函数图象上,∴5m=4(m+3),∴m=12.②当EP=AE时,点P与点D重合,∵P(m,8),E(m+3,4),P,E在反比例函数图象上,∴8m=4(m+3),∴m=3.③显然PA≠PE,若相等,则PE∥x轴,显然不可能.综上所述,满足条件的m的值为3或12.18.“六一”儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度)如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任意一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等.比如:A,B,C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI 的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米),OG=GH=HI.(1)求S1和S3的值;(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数解析式;(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?【解析】(1)∵矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等,∴弯道为反比例函数图象的一部分.设反比例函数的解析式为y =k x (k ≠0),OG =GH =HI =a ,则AG =k a ,BH =k 2a ,CI =k 3a .所以S 2=k 2a •a -k 3a•a =6,解得k =36.所以S 1=k a •a -k 2a •a =12k =12×36=18,S 3=k 3a •a =13k =13×36=12;(2)由(1)得,弯道的函数解析式为y =36x .∵T(x ,y)是弯道MN 上的任一点,∴y =36x ;(3)∵MP =2,NQ =3,∴GM =362=18,OQ =363=12.∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),∴当x =2时,y =18,可以种8棵;当x =4时,y =9,可以种4棵;当x =6时,y =6,可以种2棵;当x =8时,y =4.5,可以种2棵;当x =10时,y =3.6,可以种1棵.故一共可以种8+4+2+2+1=17(棵)花木.19、如图,已知反比例函数k y x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+. (1)试确定这两个函数的表达式;(2)求出这两个函数图象的另一个交点B 的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.【解析】(1)∵已知反比例函数k y x =经过点(1,4)A k -+,∴41k k-+=,即4k k -+= ∴2k =∴A(1,2) ∵一次函数y x b =+的图象经过点A(1,2),∴21b =+∴1b =∴反比例函数的表达式为2y x=, 一次函数的表达式为1y x =+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学专题复习:反比例函数与相似的综合题
【考点分析】
近几年的中考数学题中,对于反比例函数与几何图形的结合的考查力度明显加大,主要考查:①平面直角坐标系中,如何把线段转化为坐标,坐标转化为含有字母的代数式, 进而进行代数计算;②反比例函数与相似图形的综合题;③反比例函数与几何图形的平移。
【专题攻略】
在平面直角坐标系中,反比例函数与几何图形的综合题,最基本的解决方法是:由点的坐标求相关线段的长度,根据相关线段的长度表示点的坐标。
这类题在解答时要求我
们要熟练运用数学基础知识,还要能灵活运用数形结合、转化、待定系数、分类讨论等基本数学思想和方法。
【课前训练】
k
1、如图,面积为3的矩形OABC勺一个顶点B在反比例函数y 的图象上,另三点在坐
x
标轴上,则k= .
交于点0若厶OBA的面积为6,则k =
k
4、如图,已知双曲线y -(k>0)经过直角三角形OAB斜边
X
交于点0若厶OBC勺面积为3,贝y k = ______________
3、如图,已知双曲线
第
3、
4题
X轴于B点,若S A AOB = 3,则k =
k
y (k>0)经过直角三角形OAB斜边
x
OB的中点D,与直角边AB相
OB的中点D,与直角边AB相
【典型例题】(2010年广州中考第23题)
已知反比例函数y= m__ (m为常数)的图象经过点A (- 1, 6).
x
(1)求m的值;
(2)如图9,过点
与x轴交于点C,
(2014南沙区一模)如图,已知直线y 4 x与反比例函数y m m>0, x > 0的图象
x
交于A、B两点,与x轴、y轴分别相交于C、D两点.
(1)若点A的横坐标为1,求m的值并利用函数图象求关于x的不等式4 x< m的解集;
x
(2)是否存在以AB为直径的圆经过点P(1,0)?若存在,求出m的值;若不存在,请说明理由.
1、( 2013?宁波)如图,等腰直角三角形 / BCA=90 ° AC=BC=2 典,反比例函数
与AB , BC 交于点D , E .连结。
〔,当厶
BDE
BCA 时,
点E 的坐标为 ________________
k
2、(2013绵阳)如图,已知矩形 OABC 中,OA = 2, AB = 4,双曲线y — (k >0)与矩
x
形两边AB 、BC 分别交于E 、F 。
(1) 若E 是AB 的中点,求F 点的坐标;
(2) 若将△ BEF 沿直线EF 对折,B 点落在x 轴上的D 点,作EG 丄OC ,垂足为G , 证明△ EGDDCF ,并求k 的值。
I
解:(1) OABC 为矩形,AB=OC=4点E
是 AB 的中点,AE=2 OA=2,
k
点E (2, 2)在双曲线y=- 上,
x k=2 X 2=4,点F 在直线BC 及双 4
曲线y=—,设点F 的坐标为(4,
X 所以点F 的坐标为(4, 1).
⑵ ①证明:△ DEF 是由厶BEF 沿EF 对折得到的,
/ EDF W EBF=9(O ,点 D 在直线 OC 上,
/ GDE # CDF=180- / EDF=180-90o=90o ,
/ DGE M FCD=9O ,Z GDE # GED=90,Z CDF 2 GED
f ) ,f= 4 =1,
A 0
ABC 顶点A 在x y=
(x > 0)的图象
△ EGD^ DCF;
k ②设点E的坐标为(a ,2 ),点F的坐标为(4,b),点E、F在双曲线y=- 上,
x k=2a=4b,a=2b,所以有点E (2b,2) , AE=2b,AB=4, ED=EB=4-2b,
EG=OA=CB=2, CF=b, DF=BF=CB-CF=2-b,
DC= D匡CF2 = (2-b) 2-b2 =2 1-b ,
有点 F (4, 3), k = 4 X 4 = 3.
1
3、如图,直线y —x 2分别交轴于A C,点P是该直线与反比例函数在第一象限内的
2
一个交点,PB丄x轴于B,且s ABP 9 .
令x 0,则y 2;
令y 0,则x 4
A ( 4,0),
B (0,2)
OA 4, OC 2
S
AOC
4
△ AOC ABP
S
AOC
OC 2
ABP PB
OA
AB
△EG SA DCFDC= EG 2^/T b
ED,2-b =
2 3 ------- b= _ 4-
2b ,b 4 ,
(1)求证:△ AOC ABP ;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上T,
当厶BRT-与^ AOC相似时,求点R的坐标•
,且点R在直线PB的右侧,作RT丄x轴于
解(1) OC x 轴,PB x 轴
OC // PB
△ AOC ABP
S
AOC
S
ABP
OC 2 OA 2
PB 3,AB 3
PB 3, AB 6
OB 2
P(2,3)
p(2,3)
6
⑶ y —
x
设点R坐标为(n,-)
n
①当△ BRT ACO 时,
OA OC
BT RT
n2 2n 12 0
n, 1 .13, n21
,13(舍去)
②当△ BRTCAO 时,
OA OC
RT BT
刚42
即一
6n 2
n
n2 2n 3 0
n1 3,n21(舍去)
综合①、②所述,n 1 J3或3。
