概率统计离线作业
天津大学应用统计学离线作业及答案课件
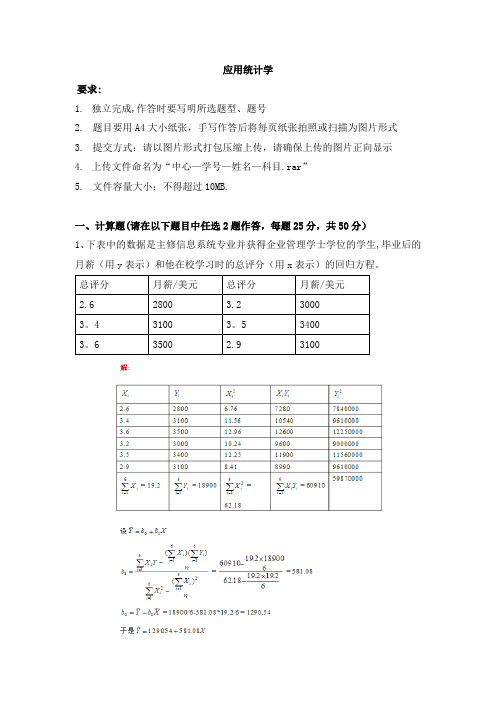
应用统计学要求:1.独立完成,作答时要写明所选题型、题号2.题目要用A4大小纸张,手写作答后将每页纸张拍照或扫描为图片形式3.提交方式:请以图片形式打包压缩上传,请确保上传的图片正向显示4.上传文件命名为“中心—学号—姓名—科目.rar”5.文件容量大小:不得超过10MB.一、计算题(请在以下题目中任选2题作答,每题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
总评分月薪/美元总评分月薪/美元2.6 28003.2 30003。
4 3100 3。
5 34003。
6 3500 2.9 31002、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的.一个随机样本由45项组成,其完成时间的样本均值为2。
39分钟,样本标准差为0。
20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
96.12=αμ3、设总体X 的概率密度函数为2(ln )2,0(,)2x0,0x x f x x μμπ--⎧>=≤⎩其中μ为未知参数,nX X X ,...,,21是来自X 的样本。
(1)试求13)(+=μμg 的极大似然估计量)(g ˆμ; (2)试验证)(gˆμ 是)(μg 的无偏估计量。
4、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?5、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。
Y ijf X 5 10 15 20yf120 0 0 8 10 18 140 3 4 3 0 10f3 4 11 10 28x6、假定某化工原料在处理前和处理后取样得到的含脂率如下表:处理前0.140 0.138 0.143 0.142 0。
2021年天津大学应用统计学离线作业及答案

应用统计学要求:1.独立完成, 作答时要写明所选题型、题号2.题目要用A4大小纸张, 手写作答后将每页纸张拍照或扫描为图片形式3.提交方法: 请以图片形式打包压缩上传, 请确保上传图片正向显示4.上传文件命名为“中心-学号-姓名-科目.rar”5.文件容量大小: 不得超出10MB。
一、计算题(请在以下题目中任选2题作答, 每题25分, 共50分)1、下表中数据是主修信息系统专业并取得企业管理学士学位学生, 毕业后月薪(用y表示)和她在校学习时总评分(用x表示)回归方程。
2、 某一汽车装配操作线完成时间计划均值为2.2分钟。
因为完成时间既受上一道装配操作线影响, 又影响到下一道装配操作线生产, 所以保持 2.2分钟标准是很关键。
一个样本由45项组成, 其完成时间样本均值为2.39分钟, 样本标准差为0.20分钟。
在0.05显著性水平下检验操作线是否达成了2.2分钟标准。
96.12=αμ3、 设总体X 概率密度函数为2(ln )21,0(,)2x0,0x e x f x x μμπ--⎧⎪>=⎨⎪≤⎩其中μ为未知参数, n X X X ,...,,21是来自X 样本。
(1)试求13)(+=μμg 极大似然估量量)(g ˆμ; (2)试验证)(gˆμ 是)(μg 无偏估量量。
4、 某商店为处理居民对某种商品需要, 调查了100户住户, 得出每个月每户平均需要量为10千克, 样本方差为9。
若这个商店供给10000户, 求最少需要准备多少这种商品, 才能以95%概率满足需要?5、依据下表中Y与X两个变量样本数据, 建立Y与X一元线性回归方程。
Y ijf X 5 10 15 20yf120 0 0 8 10 18140 3 4 3 0 10fx3 4 11 10 286、假定某化工原料在处理前和处理后取样得到含脂率以下表:处理前0.140 0.138 0.143 0.142 0.144 0.137处理后0.135 0.140 0.142 0.136 0.138 0.140假定处理前后含脂率都服从正态分布, 问处理后与处理前含脂率均值有没有显著差异。
统计学离线作业(精编文档).doc

【最新整理,下载后即可编辑】第一次作业二、主观题(共4道小题)6.指出下面的数据类型:(1)年龄数值型数据(2)性别分类型数据(3)汽车产量数值型数据(4)员工对企业某项改革措施的态度(赞成、中立、反对)顺序数据(5)购买商品时的支付方式(现金、信用卡、支票)分类数据7.某研究部门准备抽取2000个职工家庭推断该城市所有职工家庭的年人均收入。
要求:(1)描述总体和样本。
总体是“该城市所以的职工家庭”样本是“抽取的2000个职工家庭”(2)指出参数和统计量。
参数是“城市所有职工家庭的年人均收入”统计量是“抽取的2000个职工家庭”计算出的年人均收入8.一家研究机构从IT从业者中随机抽取1 000人作为样本进行调查,其中60%回答他们的月收入在5 000元以上,50%的人回答他们的消费支付方式是用信用卡。
要求:(1)这一研究的总体是什么?总体是所有的IT从业者(2)月收入是分类变量、顺序变量还是数值型变量?顺序变量(3)消费支付方式是分类变量、顺序变量还是数值型变量?分类变量(4)这一研究涉及截面数据还是时间序列数据?截面数据9.一项调查表明,消费者每月在网上购物的平均花费是200元,他们选择在网上购物的主要原因是“价格便宜”。
要求:(1)这一研究的总体是什么?总体是所有网上购物者(2)“消费者在网上购物的原因”是分类变量、顺序变量还是数值型变量?分类变量(3)研究者所关心的参数是什么?所有网上购物者的月平均花费(4)“消费者每月在网上购物的平均花费是200元”是参数还是统计量?统计量(5)研究者所使用的主要是描述统计方法还是推断统计方法?推断统计法第二次作业二、主观题(共1道小题)31.自填式、面访式、电话式各有什么长处和弱点?自填式;优点:1调查组织者管理容易,2成本低,可进行大规模调查,3对被调查者,可选择方便时间答卷,减少回答敏感问题压力。
缺点:1返回率低,2不适合结构复杂的问卷,调查内容有限,3调查周期长,4在数据搜集过程中遇见问题不能及时调整。
2020年春季《概率论与数理统计》离线考核奥鹏东师参考答案

《概率论与数理统计》
2020年春季奥鹏东北师大考核试题标准答案
试读1页答案在最后
满分100分
一、计算题(每题10分,共70分)
1、已知随机事件 的概率 ,事件 的概率 ,条件概率 ,试求事件 的概率 。
解:
因为 , ,所以
。
进而可得 。
2、设随机变量 ,且 ,试求 , 。
解:
因为随机变量 ,所以
5、若随机变量 在区间[0,1]上服从均匀分布,试求它的标准差 。
解:因为随机变量 在区间[0,1]上服从均匀分布,所以它的方差具有形式如下:
;
进而开根号可得它的标准差 ;
6、已知 ,试求 。
解:利用均值的性质可得 ;
又因为 ,所以 ;
代入上式可以求得 。
7、设 , 是取自正态总体 的一个容量为2的样本。试判断下列三个估计量是否为 的无偏估计量: , , 并指出其中哪一个方差较小。
,
由此可得 ,解得 , ;
3、已知连续型随机变量 ,试求它的密度函数 。
解:因为随机变量 服从正态分布,所以它的密度函数具有如下形式:
;
进而,将 代入上述表达式可得所求的密度函数为:
;
4、已知随机变量 的概率密度为 ,试求(1)常数 ;(2) 。
解:(1)由于
即 2A=1,A= ,所总体 的样本,所以 。
又因为 ,
,
,
所以三个估计量都是 的无偏估计;又因为
,
,
,
所以 的方差最小。
二、证明题(共30分)
设二维连续型随机向量 的联合密度函数为
证明: 与 相互独立。
证明:由二维连续型随机向量 的联合密度函数为
可得两个边缘密度函数分别为:
福建师范大学《概率统计》在线作业一003

《概率统计》在线作业一甲、乙、丙3部机床独立工作,由一个工人照管,某段时间内它们不需要工作照管的概率分别为0.9、0.8 及0.85。
则在这段时间内有机床需要工作照管的概率为()。
选项A:0.612选项B:0.388选项C:0.059选项D:0.941正确选项:B若随机变量X与Y不独立,则下面式子一定正确的是()。
选项A:E(XY)=EX*EY选项B:D(X+Y)=DX+DY选项C:Cov(X,Y)=0选项D:E(X+Y)=EX+EY正确选项:D一条自动生产线上产品的一级品率为0.6,现检查了10件,则至少有两件一级品的概率为()。
选项A:0.012选项B:0.494选项C:0.506选项D:0.988正确选项:D一模一样的铁罐里都装有大量的红球和黑球,其中一罐(取名“甲罐”)内的红球数与黑球数之比为2:1,另一罐(取名“乙罐”)内的黑球数与红球数之比为2:1,今任取一罐并从中依次取出50只球,查得其中有30只红球和20只黑球,则该罐为“甲罐”的概率是该罐为“乙罐”的概率的()。
选项A:2倍选项B:254倍选项C:798倍选项D:1024倍正确选项:D设随机事件A与B互不相容,P(A)=0.4,P(B)=0.2,则P(A|B)=()。
选项A:0选项B:0.2选项C:0.4选项D:0.5正确选项:A10个考签中有4个难签,3人参加抽签(不放回),甲先、乙次、丙最后。
则甲、乙、丙都抽到难签的概率为()。
选项A:1/30选项B:29/30选项C:1/15选项D:14/15正确选项:A甲、乙、丙3部机床独立工作,由一个工人照管,某段时间内它们不需要工作照管的概率分别为0.9、0.8 及0.85。
则在这段时间内机床因无人照管而停工的概率为()。
选项A:0.612选项B:0.388选项C:0.059选项D:0.941正确选项:C从1到2000这2000个数字中任取一数,则该数能被6整除的概率为()。
选项A:333/2000选项B:1/8选项C:83/2000选项D:1/4正确选项:A如果随机变量X和Y满足D(X+Y)=D(X-Y),则下列式子正确的是()。
东北师范大学 离线作业 概率论与数理统计

离线作业考核《概率论与数理统计》满分100分一、计算题(每题10分,共70分)1、已知随机事件A 的概率5.0)(=A P ,事件B 的概率6.0)(=B P ,条件概率8.0)|(=A B P ,试求事件B A 的概率)(B A P 。
解:因为P(A)=0.5, P(B 丨A)=0.8, 所以P(AB)= P(A)P(B 丨A)=0.4.进而可得P(AUB)=P(A)+P(B)-P(AB)= 0.7.2、设随机变量),(~p n B ξ,且28.1)(,6.1)(==X D X E ,试求n ,p 。
解:因为随机变量ξ~ B(n,p),所以E(X)=np ,D(X)=np(1-p),由此可得np=1.6, np(1-p)=1.28, 解得n=8,p=0.2;3、已知连续型随机变量)2,3(~-N X ,试求它的密度函数)(x f 。
E(3X-2)=44、已知随机变量X 的概率密度为+∞<<∞-=-x Ae x p x ,)(,试求(1)常数A ;(2){}10<<X P 。
答:(1)44或45 (2) 0.9785、若随机变量X 在区间[0,1]上服从均匀分布,试求它的标准差DX 。
解:因为随机变量X 在区间[0,1]上服从均匀分布,所以它的方差具有形式如下:12112)01(12)()(22=-=-=a b X D ;进而开根号可得它的标准差=DX 63。
又如,当随机变量X 服从区间[1,5]上的均匀分布,则2)(EX DX 的值可以如下计算:因为3)(=X E ,34)(=X D ,所以274)(2=EX DX ; 再如,设随机变量X 与Y 相互独立,且4)(,3)(==Y D X D ,则(4)16D X Y D X D Y -=+=67。
6、已知3)(,1)(=-=X D X E ,试求)]2(3[2-X E 。
解:已知3)(,1)(=-=X D X E ,则)]2(3[2-X E 可如下计算:利用均值的性质可得6)(3)]2(3[22-=-X E X E ; 又因为22))(()()(X E X D X E +=,所以4)1(3)(22=-+=X E ;代入上面式子可以求得6)]2(3[2=-X E 。
概率统计离线作业

《概率统计》作业本课程作业由二部分组成:第一部分为“客观题部分”,由15个选择题组成,每题1分,共15分; 第二部分为“主观题部分”,由4个解答题组成,第1、2题每题2.5分,第3、4题每题5分,共15分。
作业总分30分,将作为平时成绩记入课程总成绩。
客观题部分一、选择题(每题1分,共15分)1. A , B , C 三个事件中至少有两个事件,可表示为( )A 、 ABCB 、ABC ABC ABC ++C 、 _______ABC D 、ABC BC A C B A C AB +++2.设A , B , C 为任意三个事件,则_____________A B C ++=( )A 、ABCB 、ABCC 、ABC ABC ABC ++D 、A B C ++3.设A,B为任意两个事件,则( )A、()()()()P A B P A P B P AB +=+-B、()()()()P A B P A P B P AB -=--C、()()()()P A B P A P B P AB +=++D、()()()()P A B P A P B P AB -=-+4.设随机变量ξ服从参数为5的指数分布,则它的数学期望值为( ) A5 B、15 C、25 D、1255.设,[0,1],()0,[0,1].cx x p x x ∈⎧=⎨∉⎩若p(x)是一随机变量的概率密度函数,则c = ( )A 、0B 、1C 、 2D 、36.设随机变量ξ服从参数为5的指数分布,则它的方差为( ) A、125B、25 C、15 D、5 7.设A, B 为任意两个事件,则________A B +=( )A 、AB B 、ABC 、A BD 、A B +8.设a <b , 则1,()b-a 0,a x b p x ⎧≤≤⎪=⎨⎪⎩其它是( )分布的密度函数。
A 、指数B 、二项C 、均匀D 、泊松9.设总体X的均值μ与方差2σ都存在但均为未知参数,12,,,n X X X 为来自总体X的简单随机样本,记11ni i X X n ==∑,则μ的矩估计为( ) A 、X B 、1max{}i i n X ≤≤ C 、1min{}i i n X ≤≤ D 、2n 11(X )n i i X n =-∑ 10.已知事件A 与B 相互独立,且()P A B a ⋃=(a <1),P (A )=b , 则P (B ) = ( )A 、a-bB 、1-aC 、bb a --1 D 、1-b 11.当ξ服从( )分布时,必有E D ξξ=A、指数 B、泊松 C、正态 D、均匀12.设123,,X X X 为来自正态总体(,1)N μ的容量为3的简单随机样本,则( )是关 于μ得最有效的无偏估计量。
概率论与数理统计第二次在线作业

第二次在线作业1.(2.5分)A、.B、.C、.D、.我的答案:A 2.(2.5分)A、.B、.C、.D、.我的答案:B 3.(2.5分)A、.B、.C、.D、.我的答案:D 4.(2.5分)A、.B、.C、.D、.我的答案:B 5.(2.5分)A、.B、.C、.D、.我的答案:B 6.(2.5分)A、.B、.C、.D、.我的答案:C 7.(2.5分)A、.B、.C、.D、.我的答案:D 8.(2.5分)A、.B、.C、.D、.我的答案:D 9.(2.5分)A、.B、.C、.D、.我的答案:D 10.(2.5分)A、.B、.C、.我的答案:A 11.(2.5分)A、.B、.C、.D、.我的答案:C 12.(2.5分)A、.B、.C、.D、.我的答案:D 13.(2.5分)A、.B、.C、.D、.我的答案:C 14.(2.5分)B、.C、.D、.我的答案:B 15.(2.5分)A、.B、.C、.D、.我的答案:A 16.(2.5分)A、.B、.C、.D、.我的答案:B 17.(2.5分)A、.B、.C、.D、.我的答案:D 18.(2.5分)A、.B、.C、.D、.我的答案:B 19.(2.5分)A、.B、.C、.D、.我的答案:A 20.(2.5分)A、.B、.C、.D、.我的答案:A 21.(2.5分)A、.B、.C、.D、.我的答案:D 22.(2.5分)A、.B、.C、.D、.我的答案:B 23.(2.5分)A、.B、.C、.D、.我的答案:D 24.(2.5分)A、.B、.C、.D、.我的答案:C 25.(2.5分)A、.B、.C、.D、.我的答案:A 26.(2.5分)A、.B、.C、.D、.我的答案:C 27.(2.5分)A、.B、.C、.D、.我的答案:C 28.(2.5分)A、.B、.C、.D、.我的答案:C 29.(2.5分)A、.B、.C、.D、.我的答案:A 30.(2.5分)A、.B、.C、.D、.我的答案:D 31.(2.5分)A、.B、.C、.D、.我的答案:C 32.(2.5分)A、.B、.C、.D、.我的答案:B 33.(2.5分)A、.B、.C、.D、.我的答案:C 34.(2.5分)A、.B、.C、.D、.我的答案:D 35.(2.5分)A、.B、.C、.D、.我的答案:D 36.(2.5分)A、.B、.C、.D、.我的答案:D 37.(2.5分)A、.B、.C、.D、.我的答案:D 38.(2.5分)A、.B、.C、.D、.我的答案:A 39.(2.5分)A、.B、.C、.D、.我的答案:B 40.(2.5分)A、.B、.C、.D、.我的答案:D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《概率统计》作业
本课程作业由二部分组成:第一部分为“客观题部分”,由15个选择题组成,每题1分,共15分; 第二部分为“主观题部分”,由4个解答题组成,第1、2题每题2.5分,第3、4题每题5分,共15分。
作业总分30分,将作为平时成绩记入课程总成绩。
客观题部分
一、选择题(每题1分,共15分)
1. A , B , C 三个事件中至少有两个事件,可表示为( D )
A 、 ABC
B 、AB
C ABC ABC ++
C 、 _______
ABC D 、ABC BC A C B A C AB +++
2.设A , B , C 为任意三个事件,则_____________
A B C ++=( D )
A 、ABC
B 、ABC
C 、ABC ABC ABC ++
D 、A B C ++
3.设A,B为任意两个事件,则( ) A
A、()()()()P A B P A P B P AB +=+-
B、()()()()P A B P A P B P AB -=--
C、()()()()P A B P A P B P AB +=++
D、()()()()P A B P A P B P AB -=-+
4.设随机变量ξ服从参数为5的指数分布,则它的数学期望值为( ) A A5 B、1
5 C、25 D、1
25
5.设,[0,1],
()0,
[0,1].cx x p x x ∈⎧=⎨∉⎩若p(x)是一随机变量的概率密度函数,则c = ( C )
A 、0
B 、1
C 、 2
D 、3
6.设随机变量ξ服从参数为5的指数分布,则它的方差为( ) A A、125
B、25 C、15 D、5 7.设A, B 为任意两个事件,则________
A B +=( B )
A 、A
B B 、AB
C 、A B
D 、A B +
8.设a <b , 则1,()b-a 0,a x b p x ⎧≤≤⎪=⎨⎪⎩其它
是( C )分布的密度函数。
A 、指数
B 、二项
C 、均匀
D 、泊松
9.设总体X的均值μ与方差2σ都存在但均为未知参数,12,,,n X X X 为来自总体X的简单随机样本,记1
1n
i i X X n ==∑,则μ的矩估计为( A ) A 、X B 、1max{}i i n X ≤≤ C 、1min{}i i n X ≤≤ D 、2n 1
1(X )n i i X n =-∑ 10.已知事件A 与B 相互独立,且()P A B a ⋃=(a <1),P (A )=b , 则P (B ) = ( A )
A 、a-b
B 、1-a
C 、b
b a --1 D 、1-b 11.当ξ服从( )分布时,必有E D ξξ= A
A、指数 B、泊松 C、正态 D、均匀
12.设123,,X X X 为来自正态总体(,1)N μ的容量为3的简单随机样本,则( B )是关 于μ得最有效的无偏估计量。
A 、123111X X X 236++
B 、123111X X X 333
++ C 、1230.1X 0.2X 0.7X ++ D 、1230.3X 0.3X 0.4X ++
13.设(,ξη)是二维离散型随机向量,则ξ与η独立的充要条件是( ) C A、()()()E E E ξηξη⋅=⋅ B、()()()D D D ξηξη+=+ C、ξ与η不相关 D、对(,ξη)的任何可能的取值(,i j x y ),都有
}{}{},{j i j i y P x P y x P =⨯====ηξηξ
14.设12,,
,n X X X 为来自总体2(,)N μσ的简单随机样本,2σ未知,则μ的置 信区间是(B )
A
、/2/2(X Z X Z αα-+
B
、/2/2(X Z X Z αα-+ C 、()()
⎪⎪⎭
⎫ ⎝⎛-+----n S n t X n S n t X 1,12121αα D
、/2/2(((X t n X t n αα--+- 15.若12,,,n X X X 为来自总体2(,)N μσ的简单随机样本,则统计量 2211
()n i i X μσ=-∑服从自由度为( )的2χ-分布。
A
A、n B、n-1 C、n-2 D、n-3
主观题部分
二、解答题(第1、2题每题2.5分,第3、4题每题5分,共15分)
1. 简述事件独立与互斥之间的关系。
答: 独立事件指某件事情发生与否对其他事件发生情况没有影响,其对象可以是多人;互斥事件对象只能是两个,若甲事件发生,则乙事件必不能发生,且,甲乙两事件发生的概率和为1。
所以 互斥事件一定是独立事件,独立事件不一定是互斥事件。
答:一般来讲两者之间没有什么必然联系。
两个事件A,B 互斥指的是AB,此时必然有P(A+B)=P(A)+P(B)。
而相互独立指的是
P(AB)=P(A)P(B).由加法公式
P(A+B)=P(A)+P(B)-P(AB),可知除非A ,B 中有一个的概率为零,否则好吃不会独立,独立
不会互斥。
2. 简述连续型随机变量的分布密度和分布函数之间的关系。
设连续型随机变量X有密度函数p(x)和分布函数F(x) 则两者的关系为 F(x)=P(X<=x)=∫(下限是负无穷,上限是x)p(v)dv p(x)=F(x)的导数
答:分布密度刻画了随机变量在单位长度内的大小,分布函数则是小于某点的整个事件的概率,分布密度刻有分布函数求导而得,分布函数刻有分布密度求几分得到。
3. 两台机床加工同样的零件,第一台出现废品的概率为0.04,第二台出现废品的概率为0.03,加工出来的零件放在一起。
并且已知第一台加工的零件比第二台加工的零件多两倍,求任意取出的一个零件是合格品的概率。
1解:设第二台加工的零件为x个,因为第一台加工的比第二台的多两倍,则第一台加工的零件为3x个。
则,混合起来的废品数为0.04*3x+0.03*x=0.15x 易知该事件属于古典概型,所以抽出废品的概率为: 0.15x/4x=3/80
而抽出为合格品与抽出为废品两个事件为互斥事件,所以抽出的为合格品的概率为1-3/80=77/80=0.9625
2解:0.96×
43+0.97×4
1
=0.9625
4.某仪器有3个独立工作的元件,它们损坏的概率均为0.1。
当一个元件损坏时仪器发生故障的概率为0.25;当两个元件损坏时仪器发生故障的概率为0.6;当三个元件损坏时仪器发生故障的概率为0.95,求仪器发生故障的概率。
4种情况仪器故障1个坏:3*0.1*0.252个坏:3*0.1*0.1*0.63个坏:0.1*0.1*0.1*0.95总=0.075+0.018+0.00095=0.09395
4种情况仪器故障1个坏:3*0.1*0.252个坏:3*0.1*0.1*0.63个坏:0.1*0.1*0.1*0.95总=0.075+0.018+0.00095=0.09395。
