梁的弯曲变形1
第6节(弯曲变形)

Mechanics of Materials
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第六章 弯曲变形 第一节 概述
Fx Fl
转角方程
EI(x)1Fx2FlxC
2 挠度方程
E Iv(x)1F x31F lx2C xD 62
EI
d2v dx2
Fx Fl
EI(x)1Fx2FlxC
2
E Iv(x)1F x31F lx2C xD 62
⑶ 确定积分常数
EI(0)1F02Fl0C0
2 E Iv(0 )1F 0 31F l0 2 C 0D 0
EI(x)b2F l x2C1
E I(x)b 2 F l x2F 2(xa)2C 2
挠度方程
EIv(x)b6F l x3C1xD1 E Iw (x ) b 6 F lx 3F 6(x a )3 C 2xD 2
⑶ 确定积分常数
v(0)E 1 I(b 6 F l03C 10D 1)0
v (l) E 1 I[ b 6 F ll3 F 6(l a )3 C 2 l D 2 ] 0
max
(0)
Fl2 3EI
(x) 0
x (3 3)l 3
(33)l F l3
F l3
vm a xv(
) 0 .0 6 4 2
3 93E I
E I
例:简支梁AB如图所示(图中a > b),承受集中载荷F作 用,梁的弯曲刚度为EI。求此梁的挠曲轴方程和转角方程, 并确定挠度的最大值。
第九章梁的弯曲变形
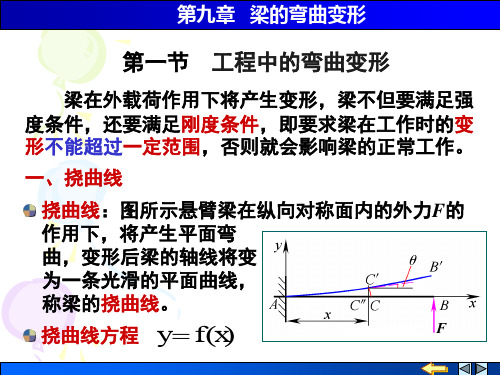
a xl
在 x l / 2处
y 0.5l
Fb
(3l 2 4b 2 ) 48 EI
yqx(l32lx2x3) 2E 4 I
A
B
ql3 24EI
x
l 2
ymax
5ql4 384EI
梁的简图
第九章 梁的弯曲变形
挠曲线方程
y6M EI(xllx)2(lx)
yC1
aB
qa4 2EI
yC2
qa4 8EI
3)叠加 y C y C 1 y C 2 2 q E 4a 8 I q E 4a I 5 8 q E 4( a I)
第九章 梁的弯曲变形
例9-5 悬臂梁跨度为 l =2m,截面为矩形,宽b = 100mm,高h =120mm,材料的弹性模量E=210GPa, 梁上载荷如图所示,求自由端A的挠度。
挠曲线方程 y f (x)
第九章 梁的弯曲变形
二、挠度和转角
挠度:截面形心线位 移的垂直分量称为该 截面的挠度,用 y 表 示,一般用 ymax 表示 全梁的最大挠度。
转角:横截面绕中性轴转动产生了角位移,此角
位移称转角,用 表示。小变形时,转角 很小,
则有以下关系:
tanydy
1
(x)
M(x) EI
曲线 y f(x)的曲率
1
(x)
(1yy2)3/2
二阶小量
y (1y2)3/2
M(x) EI
挠曲轴线 近似微分方程
y M(x) EI
第九章 梁的弯曲变形
挠曲轴线 近似微分方程
y
梁的弯曲变形测定实验

梁的弯曲变形测定实验一、预习要求1、复习材料力学有关弯曲变形内容和关于百分表的内容。
2、预习本节弄懂实验原理和测量方法。
二、实验目的1、测定钢梁在弯曲受力时的挠度f 和转角θ,并与理论计算值进行比较,以验证理论计算方法的正确性。
2、学习挠度和转角的测试方法。
三、实验装置和仪器1、弯曲梁实验装置如图1所示。
2、百分表2只、5N 砝码3块。
3、直尺、扳手等工具。
四、实验原理及方法1、实验原理弯曲梁实验装置简图如图2所示。
可以看出,钢梁AD (标号1)是外伸梁,A 、B 两处用铰链支承,载荷通过砝码2加在C 截面处,在C 、D 截面处沿位移方向安装两个百分表3和4,用以测量C 、D 两点的位移。
根据材料力学理论,钢梁1在△P 作用下,梁C 截面上的挠度f C 和B 截面转角θB 分别为图1 弯曲梁实验装置图2 弯曲梁实验装置简图EIL P f c 48)2(3∆=和 EIL P B 16)2(2∆=θ式中,123ba I =, 为对矩形梁横截面中性轴的惯性矩。
实验时,加载荷增量△P ,用百分表测出D 、C 截面处的位移增量△D 和△C ,则梁C 截面实测挠度和B 截面的实测转角分别为:C f C ∆=' ,1L D B∆='θ2、实验方法①将测量好数据的钢梁按图2所示位置要求安装在相应的卡具中,并记录有关数据,填入表1中;②将百分表3和4安装在指定位置,并检查和调整它们的工作情况。
检查时,用手轻轻下压钢梁,观察百分表上的读数是否稳定,指针走动是否均匀,能否复原;③加砝码进行实验。
载荷共分3级,每加一级后记下砝码重和百分表的读数。
实验数据按表2记录;④实验完后,卸去砝码。
表1 钢梁原始数据表表2 实验数据记录表五、实验结果处理和实验报告1、按表1和2记录实验原始数据。
2、按载荷△P 计算钢梁截面C 和截面B 上的理论挠度f C 和转角θB ,计算实测平均挠度C f '和平均转角Bθ'。
梁的平面弯曲的简介

梁的平面弯曲的简介
在平面弯曲中,荷载与支反力构成一个平面平衡力系。对 于上述三种类型的梁,支反力未知数都只有三个,由静力学可 知,平面一般力系有三个独立的平衡方程,因此这些梁的支反 力可以用静力平衡条件确定,这种梁称为静定梁。
但在实际工作中,有时需要多加支座约束,以改善梁的强 度和刚度,提高承载能力,这时支反力未知数超过三个,单凭 静力平衡条件不能完全确定其支反力,这种梁称为超静定梁或 静不定梁。解超静定梁需要考虑梁的变形、列出补充方程,与 静力平衡条件联立求解, 静定梁的分类
梁在发生平面弯曲时,外力或外力的 合力都作用在通过梁轴线的纵向平面内, 为使梁在此平面内不致发生随意的移动和 转动,必须有足够的支座约束。按支撑的 情况,常见的梁有下述三种类型。
梁的平面弯曲的简介
(1)悬臂梁:梁的一端固定,另一端自由,如图8-4(a)所示。 (2)简支梁:梁的一端为固定铰链,另一端为活动铰链支座,如 图8-4(b)所示。 (3)外伸梁:梁的支撑情况同简支梁,但梁的一端或两端伸出支 座之外,如图8-4(c)所示。
工程力学
梁的平面弯曲的简介
1.1 梁的弯曲变形
工程实际中将以弯曲为主要 变形的构件称为梁。梁的弯曲变 形是工程实际中的一种基本变形, 如桥式起重机的横梁、列车车厢 的轮轴、建筑结构中的横梁、钢 架的横梁和立柱等。本章主要讨 论的是平面弯曲。平面弯曲的受 力特点是:在过轴线的纵向对称 面内,受到垂直于轴线的荷载作 用。如图8-1所示。
工程力学
图8-1
梁的平面弯曲的简介
梁的平面弯曲变形特点 是:杆的轴线在纵向对称面 内由直线变成一光滑连续曲 线。例如图8-2所示的火车 轮轴,其因在轴的两端分别 受到垂直轴线的集中力作用 而发生平面弯曲;
梁的弯曲(工程力学课件)

02 弯曲的内力—弯矩与剪力
3-3截面
M 3 q 2a a 2qa 2
4-4截面
qa 2
5qa 2
2
M 4 FB 2a M C
3qa
2
2
5-5截面
qa 2
M 5 FB 2a
2
02 弯曲的内力—弯矩与剪力
由以上计算结果可以看出:
(1)集中力作用处的两侧临近截面的弯矩相同,剪力不同,说明剪力在
后逐段画出梁的剪力图和弯矩图。
04 弯矩、剪力与载荷集度之间的关系
例8 悬臂梁AB只在自由端受集中力F作用,如图(a)所示,
试作梁的剪力图和弯矩图。
解:
1-1截面: Q1=-F M1=0
2-2截面: Q1=-F M1=-Fl
04 弯矩、剪力与载荷集度之间的关系
例9 简支梁AB在C点处受集中力F作用,如图(a)所示,作此梁的剪力
(2)建立剪力方程和弯矩方程;
(3)应用函数作图法画出剪力Q(x),弯矩M(x)的图线,即为剪力
图和弯矩图
03 弯矩图和剪力图
例9.3 悬臂梁AB在自由端B处受集中载荷F作用,如图(a)所示,试作
其剪力图和弯矩图。
解 :(1)建立剪力方程和弯矩方程
() = ( < < )
() = −( − ) ( ≤ ≤ )
方程和弯矩方程,并作剪力图和弯矩图。
解:(1)求支反力
(2)建立剪力方程和弯矩方程
03 弯矩图和剪力图
(3)绘制剪力图、弯矩图
计算下列5个截面的弯矩值:
03 弯矩图和剪力图
二、用简便方法画剪力图、弯矩图 (从梁的左端做起)
1.无载荷作用的梁段上 剪力图为水平线。 弯矩图为斜直线(两点式画图)。
梁的弯曲变形

第7章-梁的弯曲变形(总32页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第7章 梁的弯曲变形与刚度梁弯曲变形的基本概念7.1.1 挠度在线弹性小变形条件下,梁在横力作用时将产生平面弯曲,则梁轴线由原来的直线变为纵向对称面内的一条平面曲线,很明显,该曲线是连续的光滑的曲线,这条曲线称为梁的挠曲线(图7-2)。
梁轴线上某点在梁变形后沿竖直方向的位移(横向位移)称为该点的挠度。
在小变形情况下,梁轴线上各点在梁变形后沿轴线方向的位移(水平位移)可以证明是横向位移的高阶小量,因而可以忽略不计。
挠曲线的曲线方程:)(x w w = (7-1)称为挠曲线方程或挠度函数。
实际上就是轴线上各点的挠度,一般情况下规定:挠度沿y 轴的正向(向上)为正,沿y 轴的负向(向下)为负(图7-4)。
必须注意,梁的坐标系的选取可以是任意的,即坐标原点可以放在梁轴线的任意地方,另外,由于梁的挠度函数往往在梁中是分段函数,因此,梁的坐标系可采用整体坐标也可采用局部坐标。
7.1.2 转角梁变形后其横截面在纵向对称面内相对于原有位置转动的角度称为转角(图7-3)。
转角随梁轴线变化的函数:)(x θθ= (7-2)称为转角方程或转角函数。
图7-3 梁的转角)(x 图7-2梁的挠曲线由图7-3可以看出,转角实质上就是挠曲线的切线与梁的轴线坐标轴x 的正方向之间的夹角。
所以有:xx w d )(d tan =θ,由于梁的变形是小变形,则梁的挠度和转角都很小,所以θ和θtan 是同阶小量,即:θθtan ≈,于是有:xx w x d )(d )(=θ (7-3) 即转角函数等于挠度函数对x 的一阶导数。
一般情况下规定:转角逆时针转动时为正,而顺时针转动时为负(图7-4)。
需要注意,转角函数和挠度函数必须在相同的坐标系下描述,由式(7-3)可知,如果挠度函数在梁中是分段函数,则转角函数亦是分段数目相同的分段函数。
梁的弯曲(应力、变形)

梁的弯曲类型
01
02
03
自由弯曲
梁在受到外力作用时,其 两端不受约束,可以自由 转动。
简支弯曲
梁在受到外力作用时,其 一端固定,另一端可以自 由转动。
固支弯曲
梁在受到外力作用时,其 两端均固定,不能发生转 动。
梁的弯曲应用场景
桥梁工程
桥梁中的梁常常需要进行弯曲变形以承受车辆和 行人等载荷。
稳定性。
06 梁的弯曲研究展望
CHAPTER
新材料的应用研究
高强度材料
随着材料科学的进步,高强度、轻质的新型 材料不断涌现,如碳纤维复合材料、钛合金 等。这些新材料在梁的弯曲研究中具有广阔 的应用前景,能够显著提高梁的承载能力和 刚度。
功能材料
新型功能材料如形状记忆合金、压电陶瓷等, 具有独特的力学性能和功能特性,为梁的弯 曲研究提供了新的思路和解决方案。
反复的弯曲变形可能导致疲劳裂纹的 产生和扩展,影响结构的疲劳寿命。
对使用功能的影响
弯曲变形可能导致结构使用功能受限 或影响正常使用。
04 梁的弯曲分析方法
CHAPTER
理论分析方法
弹性力学方法
01
基于弹性力学理论,通过数学公式推导梁在弯曲状态下的应力
和变形。
能量平衡法
02
利用能量守恒原理,通过计算梁在不同弯曲状态下的能量变化,
详细描述
常见的截面形状有矩形、工字形、圆形等。应根据梁的用途和受力情况选择合适的截面形状。例如, 对于承受较大弯矩的梁,采用工字形截面可以有效地提高梁的承载能力和稳定性。
支撑结构优化
总结词
支撑结构是影响梁弯曲性能的重要因素,合理的支撑结构可以提高梁的稳定性,减小梁 的变形。
梁的弯曲变形简单计算方法

梁的弯曲变形简单计算方法
梁是传动重要机构之一,其弯曲变形是广泛应用于结构力学设计中的一项重要技术。
它可
以用来分析梁承载的荷载情况,为梁的安全性能设计提供参考。
计算梁的弯曲变形是构造设计中的重要部分,因此有必要掌握有效的简便方法。
梁的弯曲变形一般是有三种计算方法:等强度线法、活荷载平移法、真实三维变形法。
这
三种计算方法的计算时间和计算精度不同,可根据实际情况选择合适的计算方法。
等强度线法是最简单且计算时间最短的方法,利用梁受力后形成的抗压线和抗张线构成图形,并将图形转化为梁形成的弯曲变形。
活荷载平移法则分析了活荷载作用于梁的变形状,将活荷载平移线与梁截面结合起来,表征出梁的弯曲变形。
而真实三维变形则完整量化了
梁的受力状态,找出真实的变形轮廓,从而获得准确的弯曲变形。
总之,梁的弯曲变形计算方法可根据实际应用场合选择合适的方法,以便为梁的设计提供参考。
在工程应用中,其梁的弯曲变形计算通常使用简便方法,如等强度线法和活荷载平
移法,而对于有特殊要求的情况,可以采用真实三维变形法,以保证梁的安全性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因为B处作用有集中力FP,所以需要分为AB和BC两
段建立弯矩方程。
28
小挠度微分方程及其积
分
积分常数的确定约束条件与连续条件-例题
解: 2. 分段建立梁的弯矩方程
于是,AB和BC两段的弯矩方程分别为
AB段 BC段
M1
x
3 4
FP x
0
x
l 4
M2
x
3 4
FP x-FP
16
基本概念
梁的位移分析的工程意义
工程设计中还有另外一类问题,所考虑的不是限制构件 的弹性位移,而是希望在构件不发生强度失效的前提下,尽量 产生较大的弹性位移。例如,各种车辆中用于减振的板簧,都 是采用厚度不大的板条叠合而成,采用这种结构,板簧既可以 承受很大的力而不发生破坏,同时又能承受较大的弹性变形, 吸收车辆受到振动和冲击时产生的动能,受到抗振和抗冲击的 效果。
41
工程中的叠加法
叠加法应用于多个载荷作用的情形
例题8-2
已知:简支梁受力
如图示,q、l、EI
均为已知。
求:C截面的挠度 wC ;B截面的转角 B
42
工程中的叠加法
叠加法应用于多个载荷作用的情形-例题
解:1.将梁上的载荷变 为3种简单的情形。
wC wC1 wC2 wC3
B B1 B2 B3
用。
三种情形下,AB段梁 的曲率(1/)处处对应相
等,因而挠度曲线具有相同 的形状。但是,在三种情形 下,由于约束的不同,梁的 位移则不完全相同。
对于没有约束的梁,因 为其在空间的位置不确定, 故无从确定其位移。
14
基本概念
梁的位移分析的工程意义
15
基本概念
梁的位移分析的工程意义
位移分析中所涉及的梁的变形和位移,都是弹性的。 工程设计中,对于结构或构件的弹性位移都有一定的限制。 弹性位移过大,也会使结构或构件丧失正常功能,即发生 刚度失效。
工程中的叠加法
叠加法应用于多个载荷作用的情形-例题
3. 应用叠加法,将简单载荷作用 时的结果分别叠加
将上述结果按代数值相加,
分别得到梁C截面的挠度和支座B
处的转角:
wC
3
wCi
i 1
11 ql 4 384 EI
,
B
3
Bi
i 1
11 48
ql 3 EI
45
工程中的叠加法
叠加法应用于 间断性分布载荷作用的情形
2
2
dx
21
小挠度微分方程及其积分
小挠度曲线微分方程
小挠度情形下
dw
2
<<
dx 1
d2w
1
dx2
3
1
dw dx
2
2
d2w M dx2 EI
弹性曲线的小挠度微分方程,式中
的正负号与w坐标的取向有关。
22
小挠度微分方程及其积分
小挠度曲线微分方程
d2w 0,M 0
46
工程中的叠加法
叠加法应用于间断性分布载荷作用的情形
对于间断性分布载荷作用的情形,根据受力 与约束等效的要求,可以将间断性分布载荷,变 为梁全长上连续分布载荷,然后在原来没有分布 载荷的梁段上,加上集度相同但方向相反的分布 载荷,最后应用叠加法。
47
工程中的叠加法
叠加法应用于多个载荷作用的情形
17
第8章 梁的弯曲变形
小挠度微分方程及其积分
18
小挠度微分方程及其积分
小挠度曲线微分方程 积分常数的确定 约束条件与连续条件
19
小挠度微分方程及其积分
小挠度曲线微分方程
20
小挠度微分方程及其积分
小挠度曲线微分方程
力学中的曲率公式
1M
ห้องสมุดไป่ตู้I
高等数学中的曲率公式
d2w
1
dx 2
3
1
dw
x
-
3 4
FP x+FP
x- l 4
l 4
x
l
积分后,得
EI1
3 8
FP x 2
C1
EIw1
1 8
FP
x3
C1x
D1
EI
=-3
2
8
FP
x 2+1 2
FP
x- l 4
2
C2
EIw2=-81
FP
x 3+1 6
FP
x- l 4
3
C2
x
D2
其中,C1、D1、C2、D2为积分常数,由支承处的约束条件和 AB段与BC段梁交界处的连续条件确定确定。
第8章 梁的弯曲变形
1
第8章 梁的弯曲变形
在平面弯曲的情形下,梁的轴线将弯曲 成平面曲线,梁的横截面变形后依然保持平面。 由于发生弯曲变形,梁横截面的位置发生改变, 这种改变称为位移。
位移是各部分变形累加的结果。位移与变 形有着密切联系,但又有严格区别。杆件横截面 的位移不仅与变形有关,而且还与杆件所受的约 束有关。
37
工程中的叠加法
在很多的工程计算手册中,已将各种支承 条件下的静定梁,在各种典型载荷作用下的挠度和 转角表达式一一列出,简称为挠度表。
基于杆件变形后其轴线为一光滑连续曲线 和位移是杆件变形累加的结果这两个重要概念,以 及在小变形条件下的力的独立作用原理,采用-叠 加法-由现有的挠度表可以得到在很多复杂情形下 梁的位移。
dx 2
d2w 0,M 0 dx 2
d2w M dx 2 EI
d2w M dx2 EI
23
小挠度微分方程及其积分
小挠度曲线微分方程
采用向下的w坐标系,有
d2w M dx2 EI
对于等截面梁,应用确定弯矩方程的方法,写出弯矩方程
M(x),代入上式后,分别对x作不定积分,得到包含积分常数的
2
第8章 梁的弯曲变形
本章将在分析变形与位移关系的基础上, 建立确定梁位移的小挠度微分方程及其积分的概 念,同时还介绍工程上应用的叠加法以及梁的刚 度设计准则。
3
第8章 梁的弯曲变形
基本概念 小挠度微分方程及其积分 工程中的叠加法 简单的静不定梁 梁的刚度设计 结论与讨论
4
第8章 梁的弯曲变形
2
4
7
l2
128
wx FP 1 x3 7 l 2 x
EI 8 128
wx
FP
1
x3
1 x
l
3
7
l 2 x
EI 8 6 4 128
据此,可以算得加力点B处的挠度和支承处A和C的转角分
别为
wB
3 256
FPl 3 EI
A
7 128
FPl 2 EI
B
- 5 128
FPl 2 EI
38
工程中的叠加法
叠加法应用于多个载荷作用的情形 叠加法应用于间断性分布载荷作用的情形
39
工程中的叠加法
叠加法应用于 多个载荷作用的情形
40
工程中的叠加法
叠加法应用于多个载荷作用的情形
当梁上受有几种不同的载荷作用时,都可以将其 分解为各种载荷单独作用的情形,由挠度表查得这 些情形下的挠度和转角,再将所得结果叠加后,便 得到几种载荷同时作用的结果。
挠度方程与转角方程:
dw M x
dx
l
EI
dx C
w
l
l
M x
EI
dx
dx
Cx
D
其中C、D为积分常数。
24
小挠度微分方程及其积分
积分常数的确定 约束条件与连续条件
25
小挠度微分方程及其积
分
积分常数的确定约束条件与连续条件
积分法中常数由梁的约束条件与连续条件确定。 约束条件是指约束对于挠度和转角的限制:
梁的挠度与转角
8
基本概念
梁的挠度与转角
梁在弯曲变形后,横截面的位置将发生改变,这种 位置的改变称为位移。梁的位移包括三部分:
横截面形心处的铅垂位移,称为挠度,用w表示;
变形后的横截面相对于变形前位置绕中性轴转
过的角度,称为转角用表示;
9
基本概念
梁的挠度与转角
横截面形心沿水平方向的位移,称为轴向位移
在下列关系: dw tan dx
在小变形条件下,挠曲线较为平
坦,即很小,因而上式中tan。
于是有
dw
dx w= w(x),称为挠度方程。
12
基本概念
梁的位移与约束密切相关
13
基本概念
梁的位移与约束密切相关
三种承受弯曲的梁
AB 段 各 横 截 面 都 受 有 相 同 的 弯 矩 ( M = Fa ) 作
43
工程中的叠加法
叠加法应用于多个载荷作用的情形-例题
2.由挠度表查得3种情形下C截 面的挠度;B截面的转角。
wC1
5 384
ql 4 EI
,
wC 2
1 48
ql 4 EI
,
wC 3
1 16
ql 4 EI
B1
1 24
ql 3 EI
,
B2
1 16
ql 3 EI
,
B3
1 3
ql 3 EI
,
44
在支座A、C两处挠度应为零,即 x=0, w1=0; x=l, w2=0
因为,梁弯曲后的轴线应为连续光滑曲线,所以AB段与BC段
梁交界处的挠度和转角必须分别相等:
x=l/4, w1=w2 ; x=l/4,1=2
32
小挠度微分方程及其积
分
积分常数的确定约束条件与连续条件-例题
