2015年7月浙江大学期末考试---高等数学基础
浙江大学《微积分(1)》历年期末考试试题

13、 求 lim(sin 2 x + cos x) x .
2
x→0
2 + cos x x2 14、 求 lim( ) . x→0 3
1
第 2 页 共 10 页
1 − 1 − x2 1 15、 若 lim = , 求: a 的值. x→0 xa 2 1 2 n n 16、 设 un = ( 1 + ( ) 1 + ) L ( 1 + ) ,求: lim un . n →∞ n n n
】
1 ( f (a ) + f (b)) . 2
三、
1、 求 2、 求
不定积分
∫x
2
2x + 1 dx . + 2x + 2 1
2
∫ ( x + 1)( x
1
2
+ 1)
dx
3、 求
∫ x ( x + 1) dx . ∫
3
4、 求
1 dx . x+5x
5、 求
arcsin e x ∫ e x dx . arctan e x ∫ e2 x dx .
x 24、 设 x > 0, 证明 f ( x) = ( x − 4) e 2 − ( x − 2)e + 2 < 0 . 2 2 25、 证明:若 e < a < b < e 2, 则 ln b − ln a > x
4 (b − a ). e2
第 4 页 共 10 页
e x sin x 26、 已知 F ( x ) = x a
5、 设 y = x ln(1 + x ) ,求: y 对 x 的 10 阶导数 y (10) ( x) .
浙江大学2014–2015春夏学期
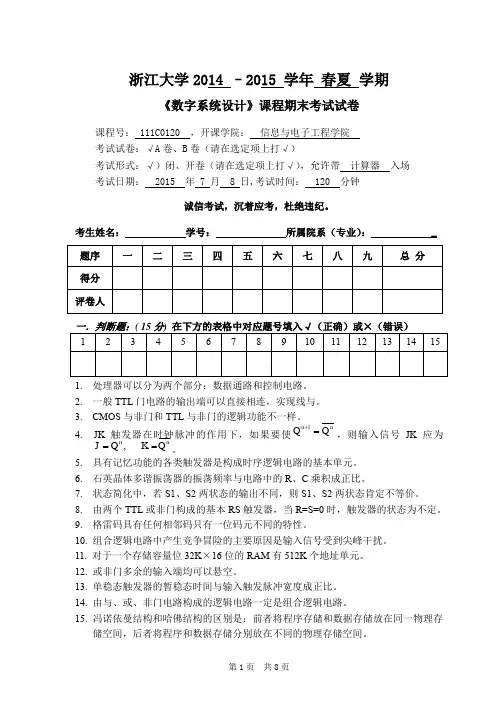
浙江大学2014 –2015 学年 春夏 学期《数字系统设计》课程期末考试试卷课程号: 111C0120 ,开课学院: 信息与电子工程学院 考试试卷:√A 卷、B 卷(请在选定项上打√)考试形式:√)闭、开卷(请在选定项上打√),允许带 计算器 入场 考试日期: 2015 年 7 月 8 日,考试时间: 120 分钟诚信考试,沉着应考,杜绝违纪。
考生姓名: 学号: 所属院系(专业): _1. 处理器可以分为两个部分:数据通路和控制电路。
2. 一般TTL 门电路的输出端可以直接相连,实现线与。
3. CMOS 与非门和TTL 与非门的逻辑功能不一样。
4. JK 触发器在时钟脉冲的作用下,如果要使n n Q Q =+1,则输入信号JK 应为nn Q K Q J ==,。
5. 具有记忆功能的各类触发器是构成时序逻辑电路的基本单元。
6. 石英晶体多谐振荡器的振荡频率与电路中的R 、C 乘积成正比。
7. 状态简化中,若S1、S2两状态的输出不同,则S1、S2两状态肯定不等价。
8. 由两个TTL 或非门构成的基本RS 触发器,当R=S=0时,触发器的状态为不定。
9. 格雷码具有任何相邻码只有一位码元不同的特性。
10. 组合逻辑电路中产生竞争冒险的主要原因是输入信号受到尖峰干扰。
11. 对于一个存储容量位32K ×16位的RAM 有512K 个地址单元。
12. 或非门多余的输入端均可以悬空。
13. 单稳态触发器的暂稳态时间与输入触发脉冲宽度成正比。
14. 由与、或、非门电路构成的逻辑电路一定是组合逻辑电路。
15. 冯诺依曼结构和哈佛结构的区别是:前者将程序存储和数据存储放在同一物理存储空间,后者将程序和数据存储分别放在不同的物理存储空间。
二、(15分)设计一位8421BCD码的判奇电路,当输入的4个码中含奇数个“1”时,输出为1,否则为0。
设输入为A,B,C,D,输出为Y。
要求使用两种方法实现:(1)用最少与非门实现,画出卡诺图,推导用与非门实现电路的最终表达式(电路图可以不画)。
数学(理)浙江大联考(七)

浙江大联考2015届高三第七次联考·数学试卷考生注意:1.本试卷共150分.考试时间120分钟.2.答题前,考生务必将密封线内的项目填写清楚.3.请将各题答案填在试卷后面的答题卷上.4.交卷时,可根据需要在加注“”标志的夹缝处进行裁剪.5.本试卷主要考试内容:高考全部内容.选择题部分(共40分)一、选择题.(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若集合A={x||2x+3|<7},B={x|y=log2(x2-4)},则A∩B等于A.{x|x<-5或x>-2}B.{x|-5<x<-2}C.{x|x≤-3或x≥-1}D.{x|x<-3或x>1}2.已知向量a=(-1,1),a+2b=(-2,k),且a与b垂直,则k的值为A.0B.2C.-1D.13.公比为2的等比数列{a n} 的各项都是正数,且 a4a10=16,则a6等于A.1B.2C.4D.84.已知函数f(x)=-则“f(1)=f(-1)”是“f(2)=4”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要和件5.一个边长为2的正方体截去两个角后所得几何体的三视图如右图所示,则该几何体的体积为A.B.C.6D.6.如图所示,已知椭圆的方程为+=1(a>b>0),A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于A. B.C. D.7.设函数f(x)=x-,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是A.(-∞,-)B.(-,0)C.(-,)D.(0,)8.如图,已知DE是边长为a正△ABC的中位线,现将△AED沿DE折起而得到△A'ED,直到平面A'ED⊥平面ABC,则A.若点M是BA'的中点,则CM∥平面A'DEB.在BC上存在点N,使得平面A'DN⊥平面BCEDC.在翻折过程中,异面直线A'D与BE所成的角先增大后减小D.在翻折过程中,直线A'B与平面A'ED所成的角的正切值可以为非选择题部分(共110分)二、填空题.(本大题共7小题,9-12每小题6分,13-15每小题4分,共36分.把答案填在答题卷中的横线上.)9.已知函数f(x)=sin(ωx-)(ω>0)的最小正周期π,则ω=▲,f()= ▲,要得到函数y=sin ωx的图象,则至少要将函数y=f(x)的图象向左平移▲个单位.10.已知过双曲线-=1的右焦点F且垂直实轴的直线与双曲线的两个交点分别为A、B,如果A、B与双曲线的左焦点构成等边三角形,则该双曲线的渐近线方程的斜率为▲;若b=2,则双曲线的焦距为▲.11.设集合A=[0,),B=[,1],函数f(x)=∈-∈则f[f(log162)]= ▲;若x0∈A,且f[f(x0)]∈A,则x0的取值范围是▲.12.设变量x,y满足约束条件---且约束条件表示的平面区域的面积为,则k=▲,目标函数z=3x-2y的取值范围为▲.13.已知两个等差数列{a n}和{b n}的前n项和分别为A n和B n,且=,则使得为整数的正整数n的个数为▲.14.设0<m<,若+-≥k恒成立,则k的最大值为▲.15.已知△ABC的三边长分别为5,6,7,点O是△ABC三个内角的角平分线的交点.若BC=7,则点集{P|=x+y,0≤x≤1,0≤y≤1}所表示的区域的面积为▲.三、解答题.(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(本小题满分15分)已知函数f(x)=sin 2x+2cos2x+3.(1)当x∈(0,)时,求函数f(x)的值域;(2)若f(x)=,且x∈(,),求sin(4x+)的值.17.(本小题满分15分)已知数列{a n}中,a1=1,前n项和为S n且S n+1=S n+1(n∈N+).(1)求数列{a n}的通项公式;(2)设数列{}的前n项和为T n,求满足不等式T n<的n值.18.(本小题满分15分)如图所示,在四棱锥A—BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.(1)当F是BC的中点时,求证:平面AEF⊥平面ABC;(2)当F在由B向C移动的过程中能否存在一个位置使得二面角F—AD—C的余弦值是.若存在,求出BF的长;若不存在,请说明理由.19.(本小题满分15分)已知抛物线C:y2=4x,定点D(m,0)(m>0).过D作直线l交抛物线C于A,B两点,E是D 点关于坐标原点O的对称点.(1)求证:∠AED=∠BED;(2)是否存在垂直于x轴的直线l'被以AD为直径的圆截得的弦长恒为定值.若存在,求出l'的方程;若不存在,请说明理由.20.(本小题满分14分)已知函数f(x)=2|x-m|和函数g(x)=x|x-m|+2m-8.(1)若m=2,求函数g(x)的单调区间;(2)若方程f(x)=2|m|在x∈[-4,+∞)上恒有唯一解,求实数m的取值范围;(3)若对任意x1∈(-∞,4],均存在x2∈[4,+∞),使得f(x1)=g(x2)成立,求实数m的取值范围.2015届高三第七次联考·数学试卷参考答案1.D 因为A={x||2x+3|<7}={x|-5<x<2},B={x|y=log2(x2-4)}={x|x2-4>0}={x|x>2或x<-2},所以A∩B={x|-5<x<-2}.2.A 由a+2b=(-2,k),a=(-1,1),得2b=(-2,k)-(-1,1)=(-1,k-1),因为a与b垂直,所以a·2b=(-1,1)·(-1,k-1)=0,解得k=0.3.B 根据等比数列的性质知a4a10==16,所以a7=4,所以a6==2.4.C f(-1)=1-(-1)=2,f(1)=a,因f(1)=f(-1),得a=2,则f(2)=22=4;反之也成立.5.B 根据三视图可以还原直观图如右图正方体截去以A,C为顶点的三棱锥余下的多面体,其体积为23-2××(×2×2)×2=.6.C 令椭圆的右端点为M,连接CM,由题意四边形OABC为平行四边形,且∠OAB=45°,B,C在椭圆上,由椭圆的对称性知,B、C关于y轴对称,可得∠COM=∠CMO=∠OAB=45°,则有∠OCM=90°,由图形知|BC|=a,且BC∥OA,故C的横坐标为a,代入椭圆方程得+=1,y=±b,结合图形知C(,b),∵△COM为等腰Rt△,∴a=b,可得c2=a2,所以e2=,e=.7.A 对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,即2mx-+2m(x-)<0在x∈[1,+∞)上恒成立,即-<0在x∈[1,+∞)上恒成立,故m<0,因为8m2x2-(1+4m2)>0在x∈[1,+∞)上恒成立,所以x2>在x∈[1,+∞)上恒成立,所以1>,解得m<-或m> (舍去),故m<-,故选A.8.D 对于A,∵BC∥平面A'DE,若CM∥平面A'DE,则平面BCM∥平面A'DE,即有BM∥平面A'DE,矛盾,故A错;对于B,若A'DN⊥平面BCED,则过点A'作平面BCED的垂线,则垂足在DN上,显然不成立,故B错;对于C,取AE的中点F,连结DF,则DF∥BE,∴∠A'DF为异面直线所成的角,在△A'DF中,A'D=,DF=a,在翻折过程中,A'F逐渐增大且最大值为,所以∠A'DF逐渐增大且小于,故C错;对于D,在翻折过程中,直线A'B与平面A'ED所成的角逐渐增大,且角最大时其正切值为,故D正确.9.2 -ω==2,f()=sin(-)=-cos=-,将函数y=f(x)的图象向左平移个单位可得到函数y=sin 2x的图象.10.±2依题意,当x=c时,y=±,由双曲线定义得-=2a⇒=±,∵b=2,∴a=,则2c=2=2.11.(,) f[f(log162)]=f[f()]=f()=;∵x0∈A,∴f(x0)=x0+∈[,1),则f[f(x0)]=2(1-x0-)=1-2x0,∵f[f(x0)]∈A,∴1-2x0∈[0,),解得<x0≤,又x0∈A,∴<x0<.12.4 (-4,3) 作出不等式对应的可行域如图,知点B(1,),C(-,)和D(1,0),则··(1--)=,解得k=4或k=-6(舍去),易知z的取值范围是(-4,3).13.5 由=,得=--==,要使为整数,则需=7+为整数,所以n=1,2,3,5,11,共有5个.14.0<m<,-=-,设-m=n,得+-=+,n>0,∵m+n=,可得2(m+n)=1,∴+=(+)×2(m+n)=2(++)≥2(+2·)=2(+2)=,当且仅当m=,n=时,+-的最小值为,∵不等式+-≥k恒成立,∴≥k恒成立,可得k的最大值为.15.易知点集{P|=x+y,0≤x≤1,0≤y≤1}所表示的区域为以OB、OC为邻边的平行四边形,其面积为2S△OBC.因为点O是△ABC三个内角的角平分线的交点,故点O到三边的距离相等,设为r,则△ABC的面积S△ABC=×(5+6+7)r=9r,设∠BAC=θ,则由余弦定理得cos θ=-=,所以sinθ=-=,则△ABC的面积S△ABC=×5×6sin θ=6,故r=,因此S△OBC=×7×=,从而所求区域的面积为.16.解:(1)由已知得f(x)=sin 2x+2cos2x+3=sin 2x+cos 2x+4=2sin(2x+)+4.当x∈(0,)时,2x+∈(,),sin(2x+)∈(-,1],故函数f(x)的值域是(3,6]. ............................................................................................................... 7分(2)由f(x)=,得2sin(2x+)+4=,∴sin(2x+)=.∵x∈(,π),∴2x+∈(,π),cos(2x+)<0,∴cos(2x+)=--=-.∴sin(4x+)=2sin(2x+)cos(2x+)=-. ......................................................................................... 15分17.解:(1)由S n+1=S n+1,得当n≥2时S n=S n-1+1,∴S n+1-S n=(S n-S n-1), 即a n+1=a n,∴=,又a1=1,得S2=a1+1=a1+a2,∴a2=,∴=,∴数列{a n}是首项为1,公比为的等比数列,∴a n=()n-1....................................................................... 7分(2)∵数列{a n}是首项为1,公比为的等比数列,∴数列{}是首项为1,公比为的等比数列,∴T n=--=3[1-()n],又∵S n=2·()n-2,∴不等式T n<,即得()n>,∴n=1或n=2. .......................................................... 15分18.解:(1)当F为中点,在△BEF中,BF=1,BE=2,∠EBF=60°,由余弦定理可得EF=,∴BF2+EF2=BE2,∴∠EFB=90°,∴EF⊥BC,又AE⊥BC且AE∩EF=E,∴BC⊥平面AEF,又BC⊂平面ABC,∴平面AEF⊥平面ABC. ....................... 6分(2)取BC的中点M,由(1)知EM⊥ED,建立如图空间直角坐标系,∵四边形EBCD是菱形,∠BED=120°,∴C(,1,0),D(0,2,0),A(0,0,2).设F(,b,0)(其中-1≤b≤1),∴=(,b-2,0),=(,-1,0),=(0,-2,2),设面ACD的法向量是n1=(x,y,z),则··⇒--令y=得x=1,z=,故n1=(1,,).设面DAF的法向量是n2=(x,y,z),∴··⇒--令y=得z=,x=2-b即n2=(2-b,,),设面DAF和面ADC所成二面角为θ,∴|cos θ|=|cos<n1·n2>|=·-=,即·-=解得b=或b=(舍去).即BF=时,使得二面角F—AD—C的余弦值是. .................................................................... 15分19.解:(1)依题意知E点坐标为(-m,0).①当直线l与x轴垂直时,根据抛物线的对称性,有∠AED=∠BED;②当l与x轴不垂直,设直线l的方程为y=k(x-m)(k≠0,m>0),A(x1,y1)B(x2,y2),则A,B两点的坐标满足方程组-消去x并整理得:ky2-4y-4km=0,∴y1+y2=,y1y2=-4m.设直线AE和BE的斜率分别为k1,k2,则k1+k2=+===-=0,∴tan∠AED+tan(180°-∠BED)=0,∴tan∠AED=tan∠BED.∵0<∠AED<,0<∠BED<,∴∠AED=∠BED,综合①②可知∠AED=∠BED. .................................................................................. 8分(2)假设存在满足条件的直线l',其方程为x=a,AD的中点为O',l'与AD为直径的圆相交于点F、G,FG 的中点为H,则O'H⊥FG,O'点的坐标为(,),∵|O'F|=|AD|=-=-,|O'H|=|a-|=|2a-x1-m|,∴|FH|2=|O'F|2-|O'H|2=[(x1-m)2+4x1]-(2a-x1-m)2=(a-m+1)x1+a(m-a),∴|FG|2=(2|FH|)2=4[(a-m+1)x1+a(m-a)].令a-m+1=0,得a=m-1,此时|FG|2=4(m-1).当m-1>0,即m>1时,|FG|=2-(定值),∴当m>1时,满足条件的直线l'存在,其方程为x=m-1;当0<m≤1时,满足条件的直线l'不存在. ........................................................................................ 15分20.解:(1)m=2时,g(x)=----函数g(x)的单调增区间为(-∞,1),(2,+∞),单调减区间为(1,2). ............................................................. 4分(2)由f(x)=2|m|在x∈[-4,+∞)恒有唯一解,得|x-m|=|m|在x∈[-4,+∞)恒有唯一解.当x-m=-m时,得x=0∈[-4,+∞);当x-m=m时,得x=2m,则2m=0或2m<-4,即m<-2或m=0.综上,m的取值范围是m<-2或m=0. ...................................................................................................................................................... 8分(3)f(x)=--则f(x)的值域应是g(x)的值域的子集.①当4≤m≤8时,f(x)在(-∞,4]上单调递减,故f(x)≥f(4)=2m-4,g(x)在[4,m]上单调递减,[m,+∞)上单调递增,故g(x)≥g(m)=2m-8,所以2m-4≥2m-8,解得4≤m≤5或m≥6.即4≤m≤5或6≤m≤8.②当m>8时,f(x)在(-∞,4]上单调递减,故f(x)≥f(4)=2m-4,g(x)在[4,]单调递增,[,m]上单调递减,[m,+∞)上单调递增,g(4)=6m-24>g(m)=2m-8,故g(x)≥g(m)=2m-8,所以2m-4≥2m-8,解得4≤m≤5或m≥6.即m>8.③0<m<4时,f(x)在(-∞,m]上单调递减,[m,4]上单调递增,故f(x)≥f(m)=1.g(x)在[4,+∞)上单调递增,故g(x)≥g(4)=8-2m,所以8-2m≤1,即≤m<4.④m≤0时,f(x)在(-∞,m]上单调递减,[m,4]上单调递增,故f(x)≥f(m)=1.g(x)在[4+∞)上单调递增,故g(x)≥g(4)=8-2m,所以8-2m≤1,即m≥(舍去).综上,m的取值范围是[,5]∪[6,+∞). ............................................................................................... 14分。
2015浙江省专升本高等数学试卷和答案

浙江省 2015年选拔优秀高职高专毕业生进入本科学习统一考试高等数学请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己的姓名、 准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
一、选择题: 本大题共5小题,每小题4分,共 20分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.当x →0x 时,f(x)是g(x)的高阶无穷小,则当x →0x 时,f(x)-g(x)是g(x)的A .等价无穷小B .同阶无穷小C .高阶无穷小D .低阶无穷小2.设f(x)在x=a 处可导,则()xx a f x a f x --+→)(lim 0等于 A. f ’(a) B.2 f ’(a) C.0 D. f ’(2a)3.设可导函数F(x)满足F ’(x)=f(x),且C 为任意常数,则A.⎰+=C x f dxx F )()(' B. ⎰+=C x F dx x f )()( C.⎰+=C x F dx x F )()( D. ⎰+=C x F dx x f )()(' 4.设直线L 1:2-31511+=-=-z y x 与L 2:⎩⎨⎧=+=32z y 1z -x ,则L 1与L 2的夹角是 A.6π B. 4π C.3π D.2π5在下列级数中,发散的是A.)1ln(1)1(11+-∑∞=-n n n B. ∑∞=-113n n n C.n n n 31)1(11∑∞=-- D . ∑∞=-113n n n非选择题部分注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2.在答题纸上作图,可先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
二、 填空题: 本大题共10小题,每小题 4分,共40分。
2015年浙江成人高考专升本高等数学一真题及答案

2015年浙江成人高考专升本高等数学一真题及答案高等数学(一)一、选择题:1~10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内.1. 当,当时,是的( )0≠b 0→x bx sin 2x A. 高阶无穷小量 B. 等价无穷小量C. 同阶但不等价无穷小量 D. 低阶无穷小量2. 设函数可导,且,则( ))(x f 2)1()1(lim=-+→f x f xx =')1(f A. 2 B. 1C.D. 0213. 函数的单调减区间为( )112)(3+-=x x x f A. B. ),(+∞-∞)2,(--∞C. D. )2,2(-),2(+∞4. 设,则( )0)(0='x f 0x x =A. 为的驻点 B. 不为的驻点)(x f )(x f C. 为的极大值点D. 为的极小值点)(x f )(x f 5. 下列函数中为的原函数的是( )xe xf 2)(=A. B.xe x e 221C. D. xe2xe226. ( )⎰=dx x x 2cos A. B. C x +-2sin 2C x +-2sin 21C. D.C x +2sin 2C x +2sin 217.( )⎰=02x t dt te dxdA. B. 2x xe 2x xe -C. D. 2x xe-2x xe--8. 设,则( )yx z ==∂∂xz A. B. 1-y yx x x yln C. D. 1-y xxxy ln 1-9. 设,则( )32y x z +==)1,1(dz A. B. dy dx 23+dy dx 32+C. D. dydx +2dydx 3+10. 级数(为非零常数)( )∑∞=-12)1(n nnkk A. 绝对收敛 B. 条件收敛C. 发散D. 收敛性与的取值有关k 二、填空题:11~20小题,每小题4分,共40分. 把答案填在题中横线上.11. _________.=+→220)1ln(lim xx x 12. 函数的间断点为_________.22)(-+=x x x f =x 13. 设,则_________.xe x y +=2=dy 14. 设,则_________.100)2(x y +=='y 15._________.⎰=-x dx316. _________.⎰-=+1121dx x x17._________.⎰=13dx e x 18. 设,则_________.x y z sin 2==∂∂xz19. 微分方程的通解为_________.x y 2='=y20. 级数的收敛半径_________.∑∞=1n nx=R 三、解答题:21~28小题,共70分. 解答应写出推理、演算步骤.21. (本题满分8分)计算.1)1sin(lim21--→x x x 22. (本题满分8分)设曲线方程为,求以及该曲线在点处的法线方程.x e y x+=0='x y )1,0(23. (本题满分8分)计算.⎰-dx xe x24. (本题满分8分)计算.⎰+edx x x 1ln 125. (本题满分8分)求曲线与直线所围图形(如图中阴影部分所示)3x y =x y =的面积.S 26. (本题满分10分)设二元函数,求的极值.522--+++=y x y xy x z z 27. (本题满分10分)求微分方程的通解.x y xy =+'128. (本题满分10分)计算,其中是由直线,及轴围成的有界区域.⎰⎰Dydxdy x 2D x y =1=x x2015年高等数学(一)试题答案一、选择题:每小题4分,共40分.1. D 2. C 3. C 4. A 5. B 6. D 7. B 8. A 9. B 10. A二、填空题:每小题4分,共40分.11. 112. 213. 14. dx e x x)2(+99)2(100x +15. 16. 0C x +--3ln 17. 18. )1(313-e x y cos 219. 20. 1Cx +2三、解答题:共70分.21. 解:xx x x x x 2)1cos(lim1)1sin(lim121-=--→→.21=22. 解:,.1+='xe y 20='=x y 曲线在点处的法线方程为,)1,0()0(211--=-x y 即.022=-+y x 23. 解:设,则,.t x =2t x =tdt dx 2=⎰⎰⋅=--tdtt e dx xe tx2⎰-=dte t 2Ce t +-=-2.C e x+-=-224. 解:⎰⎰⎰+=+ee e dxx x dx x dx x x 111ln 1ln 1eex x 121)(ln 21ln +=.23=25. 解:由对称性知⎰-=13)(2dxx x S 104241212⎪⎭⎫ ⎝⎛-=x x .21=26. 解:,.12++=∂∂y x xz12-+=∂∂y x y z 由解得⎩⎨⎧=-+=++,,012012y x y x ⎩⎨⎧=-=.11y x ,,,.222=∂∂xz12=∂∂∂y x z 222=∂∂y z ,,.2)1,1(22=∂∂=-xzA 1)1,1(2=∂∂∂=-y x zB 2)1,1(22=∂∂=-yzC ,,032<-=-AC B 0>A 因此点为的极小值点,极小值为.)1,1(-z 6-27. 解:⎪⎪⎭⎫ ⎝⎛+⎰⎰=⎰-C dx xe e y dx x dx x 11()⎰+=C dx x x21.⎪⎭⎫ ⎝⎛+=C x x 331128. 解:⎰⎰⎰⎰=Dxydyx dx ydxdy x1022⎰=10421dx x 15101x =.101=。
浙江大学城市学院2015-2016学年第一学期期末考试试卷高等数学

浙江大学城市学院2015-2016学年第一学期期末考试试卷《高等数学》一、填空或单项选择题(本题共13小题,每格2分,共30分)1、函数y =[)2,2-。
2、0tan3lim 3x x x→=。
3、函数()()3ln 2f x x x =+在1x =处的导数()513f '=。
4、函数arctan y x x =的微分2arctan 1x dy x dx x ⎛⎫=+ ⎪+⎝⎭。
5、函数12y x =+的n 阶导数为()()()11!2n n n x -+-+。
6、2323x C =+。
7、由定积分的几何意义可知,积分⎰的值为4π。
8、220sin xdx π=⎰4π。
9、121x x dx -=⎰12。
11、方程1111011x x x=的解为1x =及2x =-。
12、设1214A ⎛⎫= ⎪-⎝⎭,23B ⎛⎫= ⎪⎝⎭,则AB =810⎛⎫ ⎪⎝⎭。
13、一个口袋中装有5个黑球,3个白球,从中无放回地任取2个球,则取得的2个球恰好颜色不同的概率为1153281528C C C ⎛⎫= ⎪⎝⎭;取得的第二个球为白球的概率是38。
14、某企业有两个报警系统A 和B ,有效的概率分别为0.8和0.85,A 和B 同时有效的概率为0.7,则该企业报警系统有效的概率为 0.95 ;在A 失效的情况下B 也失效的概率为 0.25 。
二、计算下列各题(本大题共3小题,每小题6分,共18分)15、计算(1)22lim 1x x x →+∞⎛⎫- ⎪⎝⎭22lim 1xx x →+∞⎛⎫- ⎪⎝⎭; 解()()()2424422422lim 1lim 122lim 1lim 1x x x x x x x x x x e x x ⎛⎫-⋅- ⎪⎝⎭→+∞→+∞⋅⎛⎫⎛⎫-⋅-- ⎪ ⎪⎝⎭⎝⎭-→+∞→+∞⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭⎡⎤⎛⎫⎛⎫⎢⎥=-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ (直接写出4e -也给3分;能写出e 多少次方的给1分)(2)01lim sin 3xx e x→- 解:0011lim lim sin33cos33x x x x e e x x →→--==-(3分) (错一个符号的扣1分;是用洛必达法则解的,答案不是13或13-的可得1分) 16、讨论函数2xx y e =的单调性和极值。
浙江大学高等数学(上)试题册及参考答案
高数(上)试题库一、判断题1、集合{}0为空集。
( )2、集合{}1,2A =,集合{}1,3,4B =,则{}1,2,3,4A B =。
( )3、函数y x =与函数y =是相同的函数。
( )4、函数()cos f x x x =是奇函数。
( )5、函数arcsin y x =的定义域是(),-∞+∞。
( )6、函数arcsin y u =和22u x =+可以复合成函数2arcsin(2)y x =+。
( )7、函数()sin f x x =是有界函数。
( )8、函数()cos f x x =,()g x = ( ) 9、如果数列n x 发散,则n x 必是无界数列。
( ) 10、如果数列n x 无界,则n x 必是发散数列。
( ) 11、如果)(0x f =6,但00(0)(0)5,f x f x -=+=则)(lim 0x f x x →不存在。
( )12、)(x f 在0x x =处有定义是)(lim 0x f x x →存在的充分条件但非必要条件 。
( )13、0lim ()lim ()x x x x f x f x -+→→=是)(lim 0x f x x →存在的充分必要条件。
( )14、100000x是无穷大。
( )15、零是无穷小。
( ) 16、在自变量的同一变化过程中,两个无穷小的和仍为无穷小。
( )17、1sin lim=∞→xxx 。
( )18、当0x →时,sin ~~tan x x x ,则330tan sin lim lim 0sin x x x x x xx x→∞→--==。
( ) 19、)(x f 在0x 有定义,且0lim x x →)(x f 存在,则)(x f 在0x 连续。
( )20、)(x f 在0x x =无定义,则)(x f 在0x 处不连续。
( ) 21、)(x f 在[a,b]上连续,则在[a,b]上有界。
浙江大学2015年专业课844真题
浙江大学2015年专业课844真题
一、
1、判断所给系统的线性、时不变性、记忆性、因果性和稳定性。
2、一个LTI系统,已知输入x(t+1)时,输出y(t)。
给出了x(t+1)和y(t)的图像,求h(t),
用图像表示h(t)
3、给出y[n],求其Z变换(用Z域微分性质)
二、拉氏变换1求H(s)、零极图2求h(t) 3求输入为sgn(-t)+3u(t)时的零状态响应和零输入响应4画出模拟框图
三、Z变换(和拉式变换类似的问题)
四、Z变换综合,给出X(z)的若干性质,求出X(z)(教材上很多这种类型的题)
五、时域抽样定理考察,x[n]与x(nt)的关系,把教材第五章第二节看懂,很容易
以上是信号部分,貌似比以前的还要简单
六、给出了一个较复杂的逻辑等式
1 证明等式2用卡诺图化简左边3用MUX实现等式右边4写出等式的对偶形式
七、用JK触发器设计1011序列检测电路
八、有限状态机,要求写出状态转换表和状态方程,该状态米利型还是穆尔性
九、555定时器、异步时序电路和EPROM的组合电路,求CP频率,求Q2Q1Q0状态转换,求EPROM中存放的数据。
2015高考试题——数学理(浙江卷)Word版含答案
2015年普通高等学校招生全国统一考试(浙江卷)数学(理科)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中 只有一项是符合题目要求的。
1.已知集合2{20},{12}P x x x Q x x =-≥=<≤,则()R P Q =ð ( )A.[0,1)B. (0,2]C. (1,2)D. [1,2]2.某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A.38cm B. 312cm C.3323cm D. 3403cm3.已知{}n a 是等差数列,公差d 不为零,前n 项和是n S ,若348,,a a a 成等 比数列,则( )A.140,0a d dS >>B. 140,0a d dS <<C. 140,0a d dS ><D. 140,0a d dS <>4.命题“**,()n N f n N ∀∈∈ 且()nf n n ≤的否定形式是( )A. **,()n N f n N ∀∈∉,且()f n n > B. **,()n N f n N ∀∈∉或()f n n > C. **00,()n N f n N ∃∈∉且00()f n n > D. **00,()n N f n N ∃∈∉或00()f n n > 5.如图,设抛物线24y x =的焦点为F ,不经过焦点的直线上有三个不同的点,,A B C ,其中点,A B 在抛物线上,点C 在y 轴上,则BCF ∆与ACF ∆的面积之比是( )A.11BF AF -- B.2211BF AF -- C.11BF AF ++ D.2211BF AF ++6.设,A B 是有限集,定义:(,)()()d A B card A B card A B =-,其中()card A 表示有限集A 中的元素个数,命题①:对任意有限集,A B ,“A B ≠”是“ (,)0d A B >”的充分必要条件; 命题②:对任意有限集,,A B C ,(,)(,)(,)d A C d A B d B C ≤+, A. 命题①和命题②都成立 B. 命题①和命题②都不成立 C. 命题①成立,命题②不成立 D. 命题①不成立,命题②成立 7.存在函数()f x 满足,对于任意x R ∈都有( ) A. (sin 2)sin f x x = B. 2(sin 2)f x x x =+ C. 2(1)1f x x +=+ D. 2(2)1f x x x +=+8.如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CDB '--的平面角为α,则( )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≤D. 'ACB α∠≥二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2015年普通高等学校招生全国统一考试数学理试题精品解析(浙江卷)
2015年高考浙江卷理数试题解析(精编版)(解析版)一.选择题:本大题共8小题,每小题5分,共40分,在每小题的四个选项中,只有一项是符合要求的. 1. 已知集合2{20}P x x x =-≥,{12}Q x x =<≤,则()R P Q =( )A.[0,1)B. (0,2]C. (1,2)D. [1,2]2. 某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A.38cm B. 312cm C.3323cm D. 3403cm【答案】C.3. 已知{}n a 是等差数列,公差d 不为零,前n 项和是n S ,若3a ,4a ,8a 成等比数列,则( ) A.140,0a d dS >> B. 140,0a d dS << C. 140,0a d dS >< D. 140,0a d dS <>4. 命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是( )A. **,()n N f n N ∀∈∈且()f n n > B. **,()n N f n N ∀∈∈或()f n n > C. **00,()n N f n N ∃∈∈且00()f n n > D. **00,()n N f n N ∃∈∈或00()f n n >5. 如图,设抛物线24y x =的焦点为F ,不经过焦点的直线上有三个不同的点A ,B ,C ,其中点A ,B 在抛物线上,点C 在y 轴上,则BCF ∆与ACF ∆的面积之比是( )A.11BF AF -- B.2211BF AF -- C.11BF AF ++ D.2211BF AF ++6. 设A ,B 是有限集,定义(,)()()d A B card A B card A B =-,其中()card A 表示有限集A 中的元素个数,命题①:对任意有限集A ,B ,“A B ≠”是“ (,)0d A B >”的充分必要条件; 命题②:对任意有限集A ,B ,C ,(,)(,)(,)d A C d A B d B C ≤+,( )A. 命题①和命题②都成立B. 命题①和命题②都不成立C. 命题①成立,命题②不成立D. 命题①不成立,命题②成立7. 存在函数()f x 满足,对任意x R ∈都有( )A. (sin 2)sin f x x =B. 2(sin 2)f x x x =+ C. 2(1)1f x x +=+ D. 2(2)1f x x x +=+8. 如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆折成A CD '∆,所成二面角A CD B '--的平面角为α,则( )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≤D. A CB α'∠≤二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9. 双曲线2212xy-=的焦距是,渐近线方程是.10. 已知函数223,1()lg(1),1x x f x xx x ⎧+-≥⎪=⎨⎪+<⎩,则((3))f f -= ,()f x 的最小值是 . 11. 函数2()sin sin cos 1f x x x x =++的最小正周期是 ,单调递减区间是 .12. 若4log 3a =,则22a a-+= .【答案】334. 【解析】13. 如图,三棱锥A BCD -中,3,2AB AC BD CD AD BC ======,点,M N 分别是,AD BC 的中点,则异面直线AN ,CM 所成的角的余弦值是 .13. 若实数,x y 满足221x y +≤,则2263x y x y +-+--的最小值是 .15. 已知12,e e 是空间单位向量,1212e e ⋅=,若空间向量b 满足1252,2b e b e ⋅=⋅=,且对于任意,x y R ∈,12010200()()1(,)b xe ye b x e y e x y R -+≥-+=∈,则0x = ,0y = ,b = .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 16.(本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知4A π=,22b a -=122c . (1)求tan C 的值;(2)若ABC ∆的面积为3,求b 的值.17.(本题满分15分)如图,在三棱柱111ABC A B C --中,90BAC ∠=,2AB AC ==,14A A =,1A 在底面ABC 的射影为BC 的中点,D 为11B C 的中点. (1)证明:1A D ⊥平面1A B C ;(2)求二面角1A -BD-1B 的平面角的余弦值.已知函数2()(,)f x x ax b a b R =++∈,记(,)M a b 是|()|f x 在区间[1,1]-上的最大值. (1)证明:当||2a ≥时,(,)2M a b ≥;(2)当a ,b 满足(,)2M a b ≤,求||||a b +的最大值.已知椭圆2212xy+=上两个不同的点A,B关于直线12y mx=+对称.(1)求实数m的取值范围;(2)求AOB∆面积的最大值(O为坐标原点).20.(本题满分15分)已知数列{}n a满足1a=12且1na+=na-2na(n∈*N)(1)证明:112nnaa+≤≤(n∈*N);(2)设数列{}2n a的前n项和为n S,证明112(2)2(1)nSn n n≤≤++(n∈*N).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学基础试题类型高等数学基础试题类型分为单项选择题、填空题、计算题和应用题。
单项选择题的形式为四选一,即在每题的四个备选答案中选出一个正确答案;填空题只要求直接填写结果,不必写出计算过程和推理过程;计算题或应用题要求写出文字说明、演算步骤或推证过程。
四种题型分数的百分比为:单项选择题20%,填空题20%,计算题44%,应用题16%。
期末考试采用闭卷笔试形式,卷面满分为100分,考试时间为90分钟。
高等数学基础模拟题一、单项选择题1.函数2e e xx y -=-的图形关于(A )对称.(A) 坐标原点 (B) x 轴 (C) y 轴 (D) x y =2.在下列指定的变化过程中,(C )是无穷小量.(A) )(1sin∞→x x x (B) )0(1sin→x x(C) )0()1ln(→+x x (D) )(e1∞→x x3.设)(x f 在0x 可导,则=--→hx f h x f h 2)()2(lim000(C ).(A) )(0x f ' (B) )(20x f ' (C) )(0x f '- (D) )(20x f '- 4.若⎰+=c x F x x f )(d )(,则⎰=x x f xd )(ln 1(B ). (A) )(ln x F (B) c x F +)(ln (C) c x F x +)(ln 1 (D) c xF +)1( 5.下列积分计算正确的是(D ). (A) 0d sin 11=⎰-x x x (B) 1d e 0=⎰∞--x x(C) πd 2sin 0=⎰∞-x x (D) 0d cos 11=⎰-x x x6.设函数)(x f 的定义域为),(+∞-∞,则函数)()(x f x f --的图形关于(A )对称.(A) x y = (B) x 轴 (C) y 轴 (D) 坐标原点7.当0→x 时,变量(C )是无穷小量. (A)x 1 (B) x x sin (C) 1e -x(D) 2xx 8.设xx f e )(=,则=∆-∆+→∆xf x f x )1()1(lim(B ).(A) e 2 (B) e (C)e 41 (D) e 21 9.=⎰x x xf xd )(d d2(A ). (A) )(2x xf (B)x x f d )(21 (C) )(21x f (D) x x xf d )(2 10.下列无穷限积分收敛的是(B ).(A)⎰+∞d e x x (B) ⎰+∞-0d e x x (C) ⎰+∞1d 1x x (D) ⎰+∞1d 1x x二、填空题(每小题3分,共15分) 1.函数24)1ln(xx y -+=的定义域是 )2,1(- .2.若函数⎪⎩⎪⎨⎧≥+<+=00)1()(21x kx x x x f x ,在0=x 处连续,则=k e .3.曲线1)(3+=x x f 在)2,1(处的切线斜率是 3 . 4.函数x y arctan =的单调增加区间是 ),(∞+-∞ .5.若⎰+=c x x x f sin d )(,则=')(x f x sin - .6.函数)1ln(92--=x x y 的定义域是{}|13,2x x x <≤≠.7.函数⎩⎨⎧≤>-=0sin 01x x x x y 的间断点是 0x = .8.曲线1)(+=x x f 在)2,1(处的切线斜率是12. 9.函数1)1(2++=x y 的单调减少区间是 (),1-∞-.10.='⎰x x d )(sinsin x C + .三、计算题(每小题11分,共44分) 1.计算极限1)1sin(lim21-+-→x x x . 解:21)1)(1()1sin(lim 1)1sin(lim 121-=-++=-+-→-→x x x x x x x 2.设xxy 3e cos +=,求y d .解:)3(d )e (cos d )3e (cos d d xxxxy +=+=x xxxln3d 3)e (d e sin +-= x x xxxln3d 3d e sin e +-= x xxxln3)d 3e sin e (+-=3.计算不定积分⎰x x xd e21.解:由换元积分法得 c u x x xuu x x+-=-=-=⎰⎰⎰e d e )1(d e d e 121c x +-=1e4.计算定积分⎰e1d ln x x .解:由分部积分法得⎰⎰-=e 1e1e1)d(ln ln d ln x x x x x x 1d e e1⎰=-=x5.计算极限x x x 5sin 6sin lim 0→.解:00sin 6sin 661666lim lim sin 5sin 551555x x xx x x x x→→=⨯=⨯=.6.设xx y 2sin 2+=,求y '.解:()()()2sin 22sin sin 2ln 2xxy x x x ''''=+=+ 2sin cos 2ln 2x x x =+7.计算不定积分⎰x x x d 3cos .解:sin 3sin 3sin 3cos3d d d 333x x x x x x x x x x x '⎛⎫'==⋅-⋅ ⎪⎝⎭⎰⎰⎰ sin 31sin 3d 33x x x x =⋅-⎰ sin 31cos333x x x C =⋅++ 8.计算定积分⎰+e1d ln 2x xx. 解:()ee 112ln d 2ln d(2ln )xx x x x+=++⎰⎰()()()22212ln 2ln 2ln1|222ex e +++==-52=四、应用题(本题16分)1、某制罐厂要生产一种体积为V 的有盖圆柱形容器,问容器的底半径与高各为多少时用料最省? 解:设容器的底半径为r ,高为h ,则其表面积为rV r rh r S 2π2π2π222+=+= 22π4r V r S -=' 由0='S ,得唯一驻点3π2V r=,由实际问题可知,当3π2V r =时可使用料最省,此时3π4V h =,即当容器的底半径与高分别为3π2V 与3π4V时,用料最省. 2、 圆柱体上底的中心到下底的边沿的距离为l ,问当底半径与高分别为多少时,圆柱体的体积最大? 解:如图所示,圆柱体高h ,与底半径r 满足 222h r l += 圆柱体的体积公式为 2V r h π=将222r l h =-代入得()22V l h h π=-求导得()()()2222223V h lh l h ππ'=-+-=-令0V '=得h =,并由此解得r =,即当底半径为r =,高h =时,圆柱体得体积最大。
典型例题例1 计算极限32)1sin(lim21-+-→x x x x . 解 利用重要极限1sin lim0=→xxx ,及极限的运算法则得)1)(3()1sin(lim 32)1sin(lim121-+-=-+-→→x x x x x x x x )1()1sin()3(1lim 1--⋅+=→x x x x )1()1sin(lim)3(lim 111--⋅+=→→x x x x x 41141=⋅= 例2 计算极限1276lim 223+---→x x x x x .解:利用极限的运算法则得5)4(lim )2(lim )4)(3()2)(3(lim 1276lim 333223-=-+=--+-=+---→→→→x x x x x x x x x x x x x x 例3 设xx x y sin ln 3-=,求y '.解:利用导数的运算法则得xx x x x x x x x x y 2333sin ))(sin ln (sin )ln ()sin ln ('--'-='-='x x x x x x x 233sin cos )ln (sin ])(ln )[(--'-'=xx x x x x x 232sin cos )ln (sin )13(---= 例4 设2sin ln x y =,求y '.解:设2sin x u=,2x v =得u y ln = v usin = 2x v =利用复合函数求导法则,得x v u x v u y x y '⋅'⋅'='=')sin (ln 2 x v u x v u )()(sin )(ln 2'''=x v u2cos 1⋅⋅=222tan 2sin cos 2x x x x x == 例5 设yy x =()是由方程4e ln y y x +=确定的函数,求d y .解:利用导数运算法则和复合函数求导法则,等式两端分别对x 求导得左:y yy y y y x '='⋅'='1)(ln )(ln右:y y y y y x x x x x x'⋅'+='+'='+)(e )()e ()e(444 y y x '⋅+=34e由此得 y y y y x '⋅+='34e 1 整理得441e yy y x -=' 由微分定义得x yy y xd 41e d 4-= 例6 计算⎰x x xd e21.解:利用换元积分法得⎰⎰⎰-=--=)1d(e d e 1d e 11221x x x x x xx xc u u xu u +-=-=⎰e d e 1c x+-=1e例7 计算⎰x x xd ln α.解:利用分部积分法得⎰⎰⎰+-+=+=+++)(ln d 1ln 1)1(d ln d ln 111x x x x x x x x x ααααααα⎰+++-+=x xx x x d 111ln 111αααα ⎰+-+=+x x x x d 11ln 11ααααc x x x ++-+=++)1(ln 111αααα 例8 求曲线x y 22=上的点,使其到点)0,2(A 的距离最短. 解:曲线x y 22=上的点到点)0,2(A 的距离公式为22)2(y x d +-=d 与2d 在同一点取到最小值,为计算方便求2d 的最小值点,将x y 22=代入得x x d 2)2(22+-=令 2)2(2)(2+-='x d令0)(2='d 得1=x .可以验证1=x 是2d 的最小值点,并由此解出2±=y ,即曲线x y 22=上的点)2,1(和点)2,1(-到点)0,2(A 的距离最短.高等数学基础第一次作业(一) 单项选择题⒈下列各函数对中,(C )中的两个函数相等.A. 2)()(x x f =,x x g =)( B.2)(x x f =,x x g =)(C. 3ln )(x x f =,x x g ln 3)(= D. 1)(+=x x f ,11)(2--=x x x g⒉设函数)(x f 的定义域为),(+∞-∞,则函数)()(x f x f -+的图形关于(C )对称. A. 坐标原点 B. x 轴 C. y 轴 D. x y =⒊下列函数中为奇函数是(B ).A. )1ln(2x y += B. x x y cos = C. 2xx a a y -+= D. )1ln(x y +=⒋下列函数中为基本初等函数是(C ). A. 1+=x y B. x y-= C. 2xy = D. ⎩⎨⎧≥<-=0,10,1x x y⒌下列极限存计算不正确的是(D ).A. 12lim 22=+∞→x x xB. 0)1ln(lim 0=+→x xC. 0sin lim =∞→x x xD. 01sin lim =∞→xx x⒍当0→x 时,变量(C )是无穷小量. A.xxsin B. x 1 C. x x 1sin D. 2)ln(+x⒎若函数)(x f 在点0x 满足(A ),则)(x f 在点0x 连续。
