海浪谱公式总结
合集下载
海洋工程环境课件07-1-海浪要素的统计分析,海浪谱2
g 2 S() 8.110 5 exp[0.74( ) ] U
3
g2
式中：U为海面上19.5 m高处的风速。下图为不同风速 下的P-M谱分布。
PM谱的一般特性： ①与Neumann谱相比，两者比 较接近。 ②风速相同，低风速时： Neumann谱的峰值<PM谱的峰 值，高风速时：Neumann谱的 峰值>PM谱的峰值。
频率 无关，只是组成波方向 的函数，如
G ( ) An cos n
一种简单的近似处理方法是假定方向分布函数 G 与
n
2 范围内传播与分布。 2 2
为方向分布参数， ，波浪能量在主波向 ；
2 An ITTC（国际船舶拖曳水池会议）建议取n=2， 8 An ISSC（国际船舶结构会议）建议取n=4， 3 。
《海洋工程环境学》
第四章 海洋波浪
船舶工程学院 马山 副教授
5、海浪谱
前面我们讲解的都是确定性意义上的规则波理论。如线性 艾瑞波、椭圆余弦波、孤立波等。解释自然界波浪运动特征（ 深水、浅水、非线性特征等）
自然界中的海浪随时间和空间随机性地发生变化。随机过 程的海浪远比采用一个确定函数描述的规则波复杂，属于非周 期性的不规则波，各种海浪要素都是随机变量。
t an cos(nt n )
n1
相位。
an 、 n 、 n 分别是第n个余弦组成波的振幅、圆频率和
下图表示某固定点5个简谐波叠加得到的合成海面波 动结果。
5.2 频谱
对任一组成波，其单位面积波能形式为：
En ga
1 2
n
2 n
对其任意圆频率间隔 内的波能求得总 能量后再除以圆频率间隔得到的表达式为：
3
g2
式中：U为海面上19.5 m高处的风速。下图为不同风速 下的P-M谱分布。
PM谱的一般特性： ①与Neumann谱相比，两者比 较接近。 ②风速相同，低风速时： Neumann谱的峰值<PM谱的峰 值，高风速时：Neumann谱的 峰值>PM谱的峰值。
频率 无关，只是组成波方向 的函数，如
G ( ) An cos n
一种简单的近似处理方法是假定方向分布函数 G 与
n
2 范围内传播与分布。 2 2
为方向分布参数， ，波浪能量在主波向 ；
2 An ITTC（国际船舶拖曳水池会议）建议取n=2， 8 An ISSC（国际船舶结构会议）建议取n=4， 3 。
《海洋工程环境学》
第四章 海洋波浪
船舶工程学院 马山 副教授
5、海浪谱
前面我们讲解的都是确定性意义上的规则波理论。如线性 艾瑞波、椭圆余弦波、孤立波等。解释自然界波浪运动特征（ 深水、浅水、非线性特征等）
自然界中的海浪随时间和空间随机性地发生变化。随机过 程的海浪远比采用一个确定函数描述的规则波复杂，属于非周 期性的不规则波，各种海浪要素都是随机变量。
t an cos(nt n )
n1
相位。
an 、 n 、 n 分别是第n个余弦组成波的振幅、圆频率和
下图表示某固定点5个简谐波叠加得到的合成海面波 动结果。
5.2 频谱
对任一组成波，其单位面积波能形式为：
En ga
1 2
n
2 n
对其任意圆频率间隔 内的波能求得总 能量后再除以圆频率间隔得到的表达式为：
海浪谱公式总结
exp
1.03
1 TH1/
3
4
S
400.5
Hs T2
H1/ 3
2
1
5
exp1605
1
T H1/ 3
4
式中：Hs为有效波高，表示波列中波高最大的1/3波浪的平均波高； TH1/3为有效波周期，表示波列中波高最大的1/3波浪周期的平均值。
金品质•高追求 我们让你更放心！
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
m0
S
d
0
0
A
5
exp
B
4
d
A 4B
因 W /3
4
m0
1/ 2
m0
2 W /3 16
所以：B
4A
2 W /3
由于P M谱中A 0.0081g 2
0.78,
B
4A
2 W /3
3.12
2
4
W /3
代入后得ITTC谱：
S
0.78
5
exp
3.12
2
4
W /3
式中：ζw/3为三一平均波高（不是波幅）。 金品质•高追求 我们让你更放心！
典型谱画图
%1.Neumann谱 C=3.05;U=11.5;g=9.8; w=0.3:0.01:4; S1neum=C*pi/4./w.^6.*exp(-2*g^2/U^2./w.^2); plot(w,S1neum,'b-'),hold on
%2.P-M谱 a=0.0081; b=0.74; g=9.8; U=11.5; w=0.3:0.01:4; S2pm=a*g^2./(w.^5).*exp(-b*(g/U./w).^4); plot(w,S2pm,'r-'),hold on
海洋要素计算与预报(海浪7)-文档资料
F F ( , ; x , y ; t )
cg k
--------------- 二维海浪谱 --------------- 群速度
d 1 d --------------- 波向空间的群速度 c dt k d m
有限深水的弥散关系为：
gk tanh( kd )
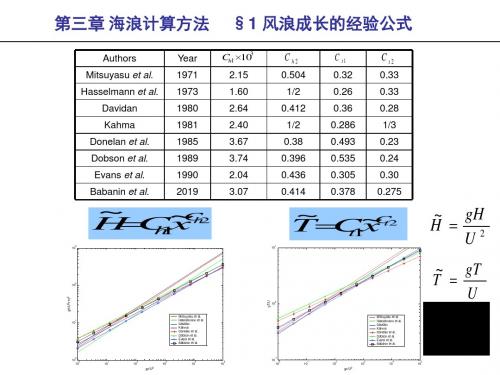
Mitsuyasu et al. Hasselmann et al. Davidan Kahma Donelan et al. Dobson et al. Evans et al. Babanin et al.
gx ~ x 2 U
10
5
10 0 10
0
10
1
10
2
10 gx/U
2
3
10
4
10
5
10
-1
10
0
10
1
10
2
10 gx/U2
3
10
4
§1 风浪成长的经验公式
10
2
10
2
10
1
10
gH/U2102
1
gH/U2102
10
0
10
0
10
-1
10 -1 10
-2
Mitsuyasu et al. Hasselmann et al. Davidan Kahma Donelan et al. Dobson et al. Evans et al. Babanin et al. 10 gT/U
§1 风浪成长的经验公式
Ch1 103
C h2
0.504 1/2 0.412 1/2 0.38 0.396 0.436 0.414
海浪谱公式总结
S f w H1 / 3 T
2
1m p
f
m
m 4 exp Tp f 4
10.Wallops谱
式中：
0.06238 mm1 / 4 m 21.057 w m 5 / 4 1 0.7458 4 m 1 TH 1 / 3 Tp 0.684 1 0.238m 1.5
0 0
A B exp d 4 5 4B A
因 W / 3 4m0 所以：B
1/ 2
m0
2
W /3
16
4A
2
W /3
由于P M谱中A 0.0081 g 2 0.78, B 代入后得ITTC谱：
4A
2
W /3
A
m1 0.30638A / B 3 / 4 T1 2m0 / m1 5.127/ B1 / 4或B 691/ T1 B W / 3 173 W /3 A 4 Bm 0 4 4 T1 代入后得到双参数海浪 谱：
2 2 4
691 173 W /3 S exp 4 4 4 5 T1 T 1
1.Neumann谱
由半经验的方法，假定海浪的某些外观特征反映其内部结构，由 观测到的波高和周期间的关系推导出来。于50年代首先提出。
2 1 2g S C exp 2 2 6 4 U
式中：U为海面上7.5米高处的风速；常数C=3.05m/s2
2.P-M谱
2
H1 / 3
4
4 1 1 5 exp1605 TH1 / 3 2
海浪谱公式总结
m，βw为两个参数，改变m即可改变谱的宽窄形状，βw用于调整
谱面积，使之等于波浪总能量。
形状参数m和JONSWAP谱中的γ一样，其选用依靠工程师的经验 和判断。一般小的无因次风距gX/U2和大的γ或m值相关，而大的无因
次风距值gX/U2导致γ=1或m=5。在浅水，上述谱中采用m=3或4是合
适的。
3.12
2
W /3
4
S
0.78
5
3.12 exp 2 4 W /3
式中：ζw/3为三一平均波高（不是波幅）。
4.双参数海浪谱
1978年第15届ITTC采用了双参数谱，双参数谱改进了ITTC谱，对成 长中的海浪也适用。
基于ITTC谱有： 1 A 3 B exp d 1 4 3/ 4 0 0 5 3B 4 3 式中：为函数， 1 0.91906 ，因此有： 4 m1 S d
11.方向谱
长峰不规则波是假定海浪沿单一方向传播的；实际海浪除了沿 主方向传播外，还向其他方向扩散，称为短峰不规则波；短峰不规则 波可以看成传播方向不同的长峰不规则波叠加而成。描述海浪沿不同 方向组成的波谱，称为方向谱。
S , S D,
式中：S(ω)为长峰不规则波的海浪谱；θ为组成波与主浪向的夹角。
9.六参数谱
奥启和汉伯尔(Ochi，Hubble， 1976)提出了一个六参数谱公式， 它把整个谱分成低频部分和高频部分两个组成部分，每一部分分别用 三个参数—有效波高Hs、谱峰频ωp和形状参数λ表示。
4 j 1 4 mj 4 2 H sj 4 j 1 mj 1 4 S exp 4 j 1 4 j j 4
第四章 海浪观测
H /m 0.6 1.4 1.6 1.1 1.6 2.1 1.1 3.0 2.6 1.7 1.5 3.9 3.0 2.4 3.3 2.0 1.1 2.5 2.1 3.5
T /s 11.4 6.6 6.5 5.3 8.3 6.0 23.0 6.9 6.9 8.8 4.5 7.1 8.1 16.1 6.2 6.4 6.2 5.8 5.3 7.1
波高模比系数
Ki
波高分组
Hi / m
出现次数
ni
区间频率
fi
平均频率
fi / ∆H H
累积次数
累积频率
F /%
∑n
6 2 3 6 11 20 30 39 57 80 94 98
i
1 2.4~2.2 2.2~2.0 2.0~1.8 1.8~1.6 1.6~1.4 1.4~1.2 1.2~1.0 1.0~0.8 0.8~0.6 0.6~0.4 0.4~0.2 0.2~0.0
2 ．波高的经脸概率分布
为了探求波高的分布规律， 为了探求波高的分布规律，必须绘制频率直方图 ,以下 以下 所示的波浪观测序列为例简述其绘制方法。 表1所示的波浪观测序列为例简述其绘制方法。 所示的波浪观测序列为例简述其绘制方法
H /m 2.0 3.0 2.5 3.1
T /s 9.2 6.6 6.6 6.9 8.6 7.1 5.4 7.1 6.6 7.5 8.1 8.1 4.3 5.4 7.5 6.8 6.6 4.5 4.9 6.2
H /m 0.8 2.5 4.1 3.8 1.7 1.0 2.0 1.8 2.0 1.8 1.3 1.3 1.5 1.0 2.0 1.4 0.3 1.3 2.0 2.0
T /s 4.5 6.6 7.3 7.9 6.9 5.3 5.8 5.8 9.4 8.3 9.6 6.8 5.4 4.1 5.8 7.5 3.6 10.5 8.4 8.1
第七章 波浪理论及其计算原理
第七章 波浪理论及其计算原理在自然界中；常可以观察到水面上各式各样的波动，这就是常讲的波浪运动，它造成海洋结构的疲劳破坏，也影响船的航行和停泊的安全。
波浪的动力作用也常引起近岸浅水地带的水底泥沙运动，致使岸滩崩塌，建筑物前水底发生淘刷，港口和航道发生淤积，水深减小，影响船舶的通航和停泊。
为了海洋结构物、驾驶船舶和船舶停靠码头的安全，必须对波浪理论有所了解。
一般讲，平衡水面因受外力干扰而变成不平衡状态，但表面张力、重力等作用力则使不平衡状态又趋于平衡，但由于惯性的作用。
这种平衡始终难以达到，于是，水体的自由表面出现周期性的有规律的起伏波动，而波动部位的水质点则作周期性的往复振荡运动。
这就是波浪现象的特性。
波浪可按所受外界的干扰不同进行分类。
由风力引起的波浪叫风成波。
由太阳、月亮以及其它天体引起的波浪叫潮汐波。
由水底地震引起的波浪叫地震水波由船舶航行引起的波浪叫船行波。
其中对海洋结构安全影响最大的是风成波。
风成波是在水表面上的波动，也称表面波。
风是产生波动的外界因素，而波动的内在因素是重力。
因此，从受力的来看；称为重力波。
视波浪的形式及运动的情况，波浪有各种类型。
它们可高可低，可长司短。
波可是静止的一一驻波（即两个同样波的相向运动所产生的波，也可以是移动的——推进波以一定的速度将波形不变地向一个方向传播的波），可以是单独的波，也可以是一个接一个的一系列波所组成的波群。
§7-1 液体波动理论一、流体力学基础1、速度场 描述海水质点的速度随空间位置和时间的变化规律的一个矢量。
),,,(t z y x V V =它的三个分量为：x 方向的量：),,,(t z y x u u =y 方向的量：),,,(t z y x v v =z 方向的量：),,,(t z y x w w =2、速度势 对于作无旋运动的液体，存在一个函数，它能反映出速度的变化，但仅仅是反映速度大小的变化，这个函数称为速度v的势函数，简称速度势： ),,,(t z y x φφ=3、速度与速度势的关系x u ∂∂=φ， y v ∂∂=φ， zw ∂∂=φ 二、海水运动的基本假设1、海水无粘性，只有重力是唯一的外力；2、液体自由液面上的压力为常数；3、液体波动振幅相对于波长为无限小；4、液体作无旋运动。
海浪谱公式总结.
皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据，于1964
年提出。适用于充分成长的海浪。
4 ag g S 5 exp U 式中：a=0.0081; β=0.74; 2
g为重力加速度； U为离海面19.5m处的风速。
8.斯科特谱
斯科特(Scott，1965)对于充分发展的海浪建议用下列谱公式:
1/ 2 2 2 p S 0.214H s exp 0 . 065 0 . 26 p
式中：-0.26<ω-ωp<1.65, Hs为有效波高；ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
b.由波高和波浪周期表示的谱公式
0.159 Tp 1 2 exp 2 2
1948 S 319 .34 4 5 3.3 4 Tp Tp
2
W /3
式中：Tp为谱峰周期，波谱峰值对应的周期。
0 0
A B exp d 4 5 4B A
因 W / 3 4m0 所以：B
1/ 2
m0
2
W /3
16
4A
2
W /3
由于P M谱中A 0.0081 g 2 0.78, B 代入后得ITTC谱：
4A
2
W /3
P一M谱为经验谱，依据的资料比较充分，分析方法合理，使用也方便。
目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅包 含一个参数U，不足以表征复杂的海浪情况。
3. ITTC谱
年提出。适用于充分成长的海浪。
4 ag g S 5 exp U 式中：a=0.0081; β=0.74; 2
g为重力加速度； U为离海面19.5m处的风速。
8.斯科特谱
斯科特(Scott，1965)对于充分发展的海浪建议用下列谱公式:
1/ 2 2 2 p S 0.214H s exp 0 . 065 0 . 26 p
式中：-0.26<ω-ωp<1.65, Hs为有效波高；ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
b.由波高和波浪周期表示的谱公式
0.159 Tp 1 2 exp 2 2
1948 S 319 .34 4 5 3.3 4 Tp Tp
2
W /3
式中：Tp为谱峰周期，波谱峰值对应的周期。
0 0
A B exp d 4 5 4B A
因 W / 3 4m0 所以：B
1/ 2
m0
2
W /3
16
4A
2
W /3
由于P M谱中A 0.0081 g 2 0.78, B 代入后得ITTC谱：
4A
2
W /3
P一M谱为经验谱，依据的资料比较充分，分析方法合理，使用也方便。
目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅包 含一个参数U，不足以表征复杂的海浪情况。
3. ITTC谱
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D(ω,θ)的一般形式为： D, kncon s (|θ|≤π)
W /3
3 . 12
2
4
W /3
代入后得 ITTC 谱：
S0 .75 8exp3 2W .1 /324
式中：ζw/3为三一平均波高（不是波幅）。
4.双参数海浪谱
1978年第15届ITTC采用了双参数谱，双参数谱改进了ITTC谱，对成 长中的海浪也适用。
基于 ITTC 谱有：
m1
S
d
0
0
9.六参数谱
奥启和汉伯尔(Ochi，Hubble， 1976)提出了一个六参数谱公式， 它把整个谱分成低频部分和高频部分两个组成部分，每一部分分别用 三个参数—有效波高Hs、谱峰频ωp和形状参数λ表示。
S1 4j
44 j1m4jj j
H 4sj2 j1exp44 j1 mj4
式中：j=1、2分别表示低频和高频部分。 六参数谱可表达任何发展阶段的风浪谱。
1.Neumann谱
由半经验的方法，假定海浪的某些外观特征反映其内部结构，由 观测到的波高和周期间的关系推导出来。于50年代首先提出。
SC416expU22g22
式中：U为海面上7.5米高处的风速；常数C=3.05m/s2
2.P-M谱
皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据，于1964 年提出。适用于充分成长的海浪。
6.JONSWAP谱
b.由波高和波浪周期表示的谱公式
S
31 .39 T 4 p2 4W /3 5 1 T p9 4 3 4.3e8x p 0.12 5 T 2p 9 12
式中：Tp为谱峰周期，波谱峰值对应的周期。
7.Bretschneider谱
布氏于1959年由无因次波高和无因次波长的联合分布函数导出二参数 谱，适用于成长阶段或者充分成长的风浪。后经日本光易恒(Mitsuyasu)改进 如下：
10.Wallops谱
1981年，美国Huang等基于理论研究和美国航空航天局wallops飞 行中心风浪流水槽实验资料，提出通用的二参数谱—wallops。他们认 为此谱适用于波浪发展、成熟和衰减各个阶段。合田把它改进成下列 形式，建议用于工程设计(Goda， 1999)
Sf w H 1/32T p1 m f m ex m p 4T pf 4
A 5
exp
B 4
d
1 3
A B 3/4
1
3 4
式中： 为函数，
1
3 4
0 .91906
，因此有：
m1 0 .30638 A / B 3 / 4
T1 2 m 0 / m1 5 .127 / B 1 / 4或 B 691 / T14
A 4Bm0
B 2 W /3 4
173
2
a.由风速和风程表示的谱公式
S
g 5 2ex p 1.2 5p 4 ex p 2 p p 2
式中：α为无因次常数，可取α=0.0076(gx/U2)-0.22; x为风区长度(风程)；U为平均风速； ωp为谱峰频率，可取 ωp=22(g/U)(gx/U2)-0.33 ; γ为谱峰提升因子，平均值为3.3； σ为峰形参数，当ω≤ωp时，可取 σ=0.07；当ω>ωp时，取σ=0.09.
10.Wallops谱
式中：
w40.m 056/42m 3m 8m 11/4 10.745m 821.057
Tp 10.23T8m H1/31.50.684
m，βw为两个参数，改变m即可改变谱的宽窄形状，βw用于调整 谱面积，使之等于波浪总能量。
形状参数m和JONSWAP谱中的γ一样，其选用依靠工程师的经验 和判断。一般小的无因次风距gX/U2和大的γ或m值相关，而大的无因 次风距值gX/U2导致γ=1或m=5。在浅水，上述谱中采用m=3或4是合 适的。
国际拖曳水池会议(ITTC， 1972)对P-M谱进行了修改，得到ITTC谱。
基于 P M 谱有：
m0
S
Байду номын сангаас
d
0
0
A 5
exp
B 4
d
A 4B
因
W /3
4
m0
1/2
m0
2 W /3 16
所以：
B
4A 2
W /3
由于 P M 谱中 A 0.0081 g 2
0.78 , B
4A 2
W /3
T1 4
代入后得到双参数海浪 谱：
S 1T714325W/3 expT614941
5.ISSC谱
国际船舶结构会议ISSC1964推荐下列谱公式，且常 称之为ISSC谱。
2
Sf0.11 T H 0.1 s2
f15exp0.44 T01 .1f4
6.JONSWAP谱
该谱由“北海海浪联合计划”测量分析得到，在60年代末期提 出，适合像北海那样风程被限定是海域，有两种表示形式。
8.斯科特谱
斯科特(Scott，1965)对于充分发展的海浪建议用下列谱公式:
S0.21 H s2 4ex p 0.06 5 p p 20.26 1/2
式中：-0.26<ω-ωp<1.65, Hs为有效波高；ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
式中：a=0.008S1;β=0.74;a5g2expUg4
g为重力加速度； U为离海面19.5m处的风速。 P一M谱为经验谱，依据的资料比较充分，分析方法合理，使用也方便。 目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅包 含一个参数U，不足以表征复杂的海浪情况。
3. ITTC谱
S f
0.257
Hs T2
H1/3
2
1 f5
TH1/3
exp1.03
1 TH1/3
4
S
400.5
Hs T2
H1/3
2
1
5
exp1605TH11/34
式中：Hs为有效波高，表示波列中波高最大的1/3波浪的平均波高； TH1/3为有效波周期，表示波列中波高最大的1/3波浪周期的平均值。
11.方向谱
长峰不规则波是假定海浪沿单一方向传播的；实际海浪除了沿 主方向传播外，还向其他方向扩散，称为短峰不规则波；短峰不规则 波可以看成传播方向不同的长峰不规则波叠加而成。描述海浪沿不同 方向组成的波谱，称为方向谱。
S , S D ,
式中：S(ω)为长峰不规则波的海浪谱；θ为组成波与主浪向的夹角。
W /3
3 . 12
2
4
W /3
代入后得 ITTC 谱：
S0 .75 8exp3 2W .1 /324
式中：ζw/3为三一平均波高（不是波幅）。
4.双参数海浪谱
1978年第15届ITTC采用了双参数谱，双参数谱改进了ITTC谱，对成 长中的海浪也适用。
基于 ITTC 谱有：
m1
S
d
0
0
9.六参数谱
奥启和汉伯尔(Ochi，Hubble， 1976)提出了一个六参数谱公式， 它把整个谱分成低频部分和高频部分两个组成部分，每一部分分别用 三个参数—有效波高Hs、谱峰频ωp和形状参数λ表示。
S1 4j
44 j1m4jj j
H 4sj2 j1exp44 j1 mj4
式中：j=1、2分别表示低频和高频部分。 六参数谱可表达任何发展阶段的风浪谱。
1.Neumann谱
由半经验的方法，假定海浪的某些外观特征反映其内部结构，由 观测到的波高和周期间的关系推导出来。于50年代首先提出。
SC416expU22g22
式中：U为海面上7.5米高处的风速；常数C=3.05m/s2
2.P-M谱
皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据，于1964 年提出。适用于充分成长的海浪。
6.JONSWAP谱
b.由波高和波浪周期表示的谱公式
S
31 .39 T 4 p2 4W /3 5 1 T p9 4 3 4.3e8x p 0.12 5 T 2p 9 12
式中：Tp为谱峰周期，波谱峰值对应的周期。
7.Bretschneider谱
布氏于1959年由无因次波高和无因次波长的联合分布函数导出二参数 谱，适用于成长阶段或者充分成长的风浪。后经日本光易恒(Mitsuyasu)改进 如下：
10.Wallops谱
1981年，美国Huang等基于理论研究和美国航空航天局wallops飞 行中心风浪流水槽实验资料，提出通用的二参数谱—wallops。他们认 为此谱适用于波浪发展、成熟和衰减各个阶段。合田把它改进成下列 形式，建议用于工程设计(Goda， 1999)
Sf w H 1/32T p1 m f m ex m p 4T pf 4
A 5
exp
B 4
d
1 3
A B 3/4
1
3 4
式中： 为函数，
1
3 4
0 .91906
，因此有：
m1 0 .30638 A / B 3 / 4
T1 2 m 0 / m1 5 .127 / B 1 / 4或 B 691 / T14
A 4Bm0
B 2 W /3 4
173
2
a.由风速和风程表示的谱公式
S
g 5 2ex p 1.2 5p 4 ex p 2 p p 2
式中：α为无因次常数，可取α=0.0076(gx/U2)-0.22; x为风区长度(风程)；U为平均风速； ωp为谱峰频率，可取 ωp=22(g/U)(gx/U2)-0.33 ; γ为谱峰提升因子，平均值为3.3； σ为峰形参数，当ω≤ωp时，可取 σ=0.07；当ω>ωp时，取σ=0.09.
10.Wallops谱
式中：
w40.m 056/42m 3m 8m 11/4 10.745m 821.057
Tp 10.23T8m H1/31.50.684
m，βw为两个参数，改变m即可改变谱的宽窄形状，βw用于调整 谱面积，使之等于波浪总能量。
形状参数m和JONSWAP谱中的γ一样，其选用依靠工程师的经验 和判断。一般小的无因次风距gX/U2和大的γ或m值相关，而大的无因 次风距值gX/U2导致γ=1或m=5。在浅水，上述谱中采用m=3或4是合 适的。
国际拖曳水池会议(ITTC， 1972)对P-M谱进行了修改，得到ITTC谱。
基于 P M 谱有：
m0
S
Байду номын сангаас
d
0
0
A 5
exp
B 4
d
A 4B
因
W /3
4
m0
1/2
m0
2 W /3 16
所以：
B
4A 2
W /3
由于 P M 谱中 A 0.0081 g 2
0.78 , B
4A 2
W /3
T1 4
代入后得到双参数海浪 谱：
S 1T714325W/3 expT614941
5.ISSC谱
国际船舶结构会议ISSC1964推荐下列谱公式，且常 称之为ISSC谱。
2
Sf0.11 T H 0.1 s2
f15exp0.44 T01 .1f4
6.JONSWAP谱
该谱由“北海海浪联合计划”测量分析得到，在60年代末期提 出，适合像北海那样风程被限定是海域，有两种表示形式。
8.斯科特谱
斯科特(Scott，1965)对于充分发展的海浪建议用下列谱公式:
S0.21 H s2 4ex p 0.06 5 p p 20.26 1/2
式中：-0.26<ω-ωp<1.65, Hs为有效波高；ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
式中：a=0.008S1;β=0.74;a5g2expUg4
g为重力加速度； U为离海面19.5m处的风速。 P一M谱为经验谱，依据的资料比较充分，分析方法合理，使用也方便。 目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅包 含一个参数U，不足以表征复杂的海浪情况。
3. ITTC谱
S f
0.257
Hs T2
H1/3
2
1 f5
TH1/3
exp1.03
1 TH1/3
4
S
400.5
Hs T2
H1/3
2
1
5
exp1605TH11/34
式中：Hs为有效波高，表示波列中波高最大的1/3波浪的平均波高； TH1/3为有效波周期，表示波列中波高最大的1/3波浪周期的平均值。
11.方向谱
长峰不规则波是假定海浪沿单一方向传播的；实际海浪除了沿 主方向传播外，还向其他方向扩散，称为短峰不规则波；短峰不规则 波可以看成传播方向不同的长峰不规则波叠加而成。描述海浪沿不同 方向组成的波谱，称为方向谱。
S , S D ,
式中：S(ω)为长峰不规则波的海浪谱；θ为组成波与主浪向的夹角。