数学物理方法第2章复变函数积分2020
合集下载
02复变函数微积分

(1)曲线积分法 (2)凑全微分法 (3)不定积分法
数学物理方法
应用
v( x, y ) dv
2 2 u ( x , y ) x y 例2.5 已知解析函数f(z)的实部
且f(0)=0,试求出虚部和f(z) 。 解: v u 2 y x y
v u 2x y x
数学物理方法
2 xy C
(2)凑全微分显示法
dv( x, y) 2 ydx 2 xdy d (2 xy C )
v( x, y) 2 xy C
(3)不定积分法
v u 2x y x
v u 2y x y
v 2 y ( x) x
l l
l1 l 2
f ( z )dz f ( z )dz f ( z )dz
l1 l2
l
l
f ( z )dz f ( z )dz , 其中 l 是l的逆向
l
f ( z )dz
l
f ( z ) dz
f ( z)dz
l l
f ( z ) ds
那么有
u v v u , x y x y
上式称为柯西-黎曼条件。简称(C-R条件)
数学物理方法
证明:
1)若 y 0, x 0
f ( z z ) f ( z ) u ( x x, y ) iv( x x, y ) u ( x, y ) iv( x, y ) lim z 0 z 0 z x u ( x x, y ) u ( x, y ) v( x x, y ) v( x, y ) lim i lim z 0 z 0 x x u ( x, y ) v( x, y ) i x x lim
数学物理方法
应用
v( x, y ) dv
2 2 u ( x , y ) x y 例2.5 已知解析函数f(z)的实部
且f(0)=0,试求出虚部和f(z) 。 解: v u 2 y x y
v u 2x y x
数学物理方法
2 xy C
(2)凑全微分显示法
dv( x, y) 2 ydx 2 xdy d (2 xy C )
v( x, y) 2 xy C
(3)不定积分法
v u 2x y x
v u 2y x y
v 2 y ( x) x
l l
l1 l 2
f ( z )dz f ( z )dz f ( z )dz
l1 l2
l
l
f ( z )dz f ( z )dz , 其中 l 是l的逆向
l
f ( z )dz
l
f ( z ) dz
f ( z)dz
l l
f ( z ) ds
那么有
u v v u , x y x y
上式称为柯西-黎曼条件。简称(C-R条件)
数学物理方法
证明:
1)若 y 0, x 0
f ( z z ) f ( z ) u ( x x, y ) iv( x x, y ) u ( x, y ) iv( x, y ) lim z 0 z 0 z x u ( x x, y ) u ( x, y ) v( x x, y ) v( x, y ) lim i lim z 0 z 0 x x u ( x, y ) v( x, y ) i x x lim
数学物理方法第二章复变函数的积分
d z b ln b ln a ln i Arg b Arg a az a
b
ln z ln(| z |e )
Arg z
此积分与路径有关系!因z = 0 是1/z的一个奇点。 如被积函数有奇点,则由不定积分给出的函数可能是 多值的。被积函数的奇点,可能是该函数的支点。
x d y y d x d d f ( z ) d z u v d t i u v d t l t d t t d t d t d t A A
t B t B
几个重要性质 1.常数因子可以移到积分号之外
c f ( z ) d z c f ( z ) d z
推广:若 f (z)在单连通域B上解析,在闭单连通 域 B 上连续,则沿 B 上任一分段光滑闭合曲 线 l (也可以是 B 的边界),有
l
f (z)d z 0
(二)复连通域情形 如果区域内存在: (1)奇点 ;(2)不连续线段;(3)无定义区 为了把这些奇异部分排除在外,需要作适当的 围道 l1、l2、 l3 把它们分隔开来,形成带孔的区 域—复连通区域。
C 2
只要起点和终点固定不变,当积分路径连续变形时 (不跳过“孔”)时,函数的路积分值不变。
§2.3 不定积分(原函数)
根据 Cauchy 定理,若函数 f (z) 在单连通
区域B上解析, 则沿B上任一分段光滑曲线 l
的积分
l
f ( z) dz 只与起点和终点有关,而与
路径无关。因此如果固定起点 z0 而变化终点 z, 这个不定积分便定义了一个单值函数 F(z):
l
f (z)d z 0
George Green
数学物理方法1-2复变函数的积分

莫雷拉定理
总结词
莫雷拉定理是复变函数中一个关于全 纯函数的积分性质的定理。
详细描述
莫雷拉定理说明,如果全纯函数f(z)在圆盘 |z| < R内有界,那么对于任意实数t,积分 ∫f(z)e^(it)dz在|z| = R的边界上非零。这个 定理在研究全纯函数的性质以及解决一些数 学物理问题时非常有用。
柯西定理
总结词
柯西定理是复变函数中的一个基本定理,它表明如果一个函数在某个区域内的点上满足某种条件,则 该函数在该区域内可积。
详细描述
柯西定理说明,如果函数f(z)在某个区域D内是解析的,并且存在常数C使得对于D内的任意点z,都有 |f(z)|≤C,那么函数f(z)在D内是可积的。这意味着满足一定条件的解析函数在一定区域内具有可积性。
幂级数展开的收敛性
幂级数展开的收敛性取决于函数的性质和级数的收敛条件。
幂级数展开的应用
幂级数展开在数学物理中广泛应用于求解微分方程和积分方程。
泰级数展开
泰勒级数展开定义
01
将一个复变函数表示为多项式的无穷级数。
泰勒级数展开的收敛性
02
泰勒级数展开的收敛性取决于函数的性质和级数的收敛条件。
泰勒级数展开的应用
个定理在解决一些数学物理问题时非常有用。
柯西不等式
总结词
柯西不等式是复变函数中一个基本的积分不等式,它反映了函数与其共轭函数之间的积分关系。
详细描述
柯西不等式表明,对于任意实数a和b,以及在全平面上的非负函数f和g,有∫f(z)g(z*)dz ≥ |∫f(z)dz * ∫g(z*)dz|, 其中z*是z的共轭复数。这个不等式在处理一些积分问题时非常有用。
积分路径
积分性质
复数函数的积分具有线性性质、可加 性、可交换性等基本性质。
数学物理方法课后答案 (2)

若?x在无穷远点的无心邻域在大圆弧czreirr上limz?zk一致成立则lim?zdzik?12rrcr21解上第一式表明任给0存在与argz无关的m0使当zrm时dz有z?z?k利用i?复变函数性质5及上式可证c21rz?adzdzlim?zdz?ikzzkzzk2???max???rcr1crzcrz21?由于可任意小21为常量故上式可任意地小
2
2+ 4 i
1+i
[( x 2 − y 2 ) + 2ixy ](dx + idy )
86 − 6i 3
= ∫ [ x 2 − (3 x − 2) 2 + 2ix(3 x − 2)](1 + 3i ) dx = −
(3)沿1 + i 到 2 + i ,再到 2 + 4i 的折线。
I =∫
2 1
2+ 4 i
L
∫ ∫
L
f (ξ )[
f (ξ ) Δ z ∫ L (ξ − z ) 2 (ξ − z − Δ z ) d ξ
ξ − z ( ξ − z − Δz )
2
d ξ , 现 在 讨 论 能 否 找 到 δ ( ε ), 使 当 Δ z < δ 时 d ,同 时 将 2
上 式 成 立 。 因 本 题 是 讨 论 Δ z → 0时 的 积 分 极 限 , 不 妨 令 Δ z < min z − ξ = d 代 入 有 Δ I ≤ δ
4 4 1 1 0 0
I3 = ∫ {[2(t2 + 3) + (2t)2 ]2dt + [3(2t)-(t2 + 3)]2tdt} = ∫ (24t 2 + 12 − 2t 3 − 6t )dt =
2
2+ 4 i
1+i
[( x 2 − y 2 ) + 2ixy ](dx + idy )
86 − 6i 3
= ∫ [ x 2 − (3 x − 2) 2 + 2ix(3 x − 2)](1 + 3i ) dx = −
(3)沿1 + i 到 2 + i ,再到 2 + 4i 的折线。
I =∫
2 1
2+ 4 i
L
∫ ∫
L
f (ξ )[
f (ξ ) Δ z ∫ L (ξ − z ) 2 (ξ − z − Δ z ) d ξ
ξ − z ( ξ − z − Δz )
2
d ξ , 现 在 讨 论 能 否 找 到 δ ( ε ), 使 当 Δ z < δ 时 d ,同 时 将 2
上 式 成 立 。 因 本 题 是 讨 论 Δ z → 0时 的 积 分 极 限 , 不 妨 令 Δ z < min z − ξ = d 代 入 有 Δ I ≤ δ
4 4 1 1 0 0
I3 = ∫ {[2(t2 + 3) + (2t)2 ]2dt + [3(2t)-(t2 + 3)]2tdt} = ∫ (24t 2 + 12 − 2t 3 − 6t )dt =
复变函数积分计算公式

柯西定理的重要推论: f
(n)
n! 2 i
f ( ) d l ( z)n1
即解析函数可以求导任意多次。
根据柯西定理的推论: n! f ( ) (n) f d ,可有 n 1 l 2 i ( z ) n t
n
t 0
n! 2 i
l
e 1 d n 1 ( )
l
1 xdx i 1dy i 0 0 2
1 1
I 2 [u ( x, y )dx v( x, y )dy ]
l
i [v( x, y )dx u ( x, y )dy ]
l
1 xdx 0 2
1
可见,复变函数的积分值 不仅和积分的起点与终点有关 ,而且与积分路径有关,可以 用柯西定理来描述积分值与路 径的关系。
例:计算下式积分: I (z- ) dz
l
n
分析:若l不包含点,则积分值为零,若 包含点,则当n 0时,被积函数在l所围
区域内仍解析,只有当n 0时才成为奇点, 则在圆周上,z- =Re
i
现做一圆将点包围,圆心为,半径为C,
I
l
( z ) dz
n
R e Re id
第二章
复变函数的积分
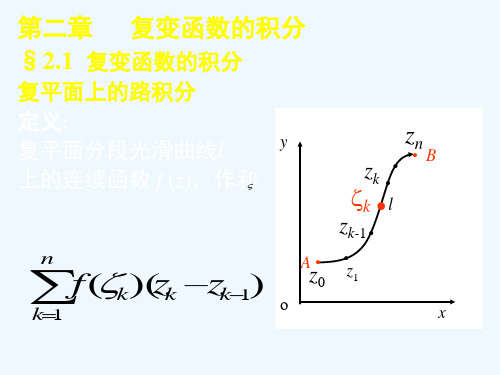
设在复数平面的某分段光滑曲线l上 定义了连续函数f ( z )在l上取一系列 zn (即终 点B), 把l分成 n 个小段,在每个小段
的分点z0 (即起点A),z1 z2
zK 1 , zK 上任取一点 K ,作和:
f ( ) z
K 1 K
n
K
z K 1
数学物理方法 第二章 复变函数的积分

wuxia@
证明: 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较,只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点,因此,以α为圆心,取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理, ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有:z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有: 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续,一定可以找到∆ > 0,当 | z − α |≤ ∆时, | f ( z ) − f (α ) |≤ ε ′ 因而有: 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
证明: 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较,只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点,因此,以α为圆心,取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理, ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有:z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有: 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续,一定可以找到∆ > 0,当 | z − α |≤ ∆时, | f ( z ) − f (α ) |≤ ε ′ 因而有: 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
数学物理方法课件-2 复变积分

其中,M (R) max f (z) , n 1,2, z R
证:
f (n) ( )
n!
2i
(
f ( ) )n1
d
n!
2
M (R) R n 1
2R
n!M (R) Rn
即
f
(n) ( )
n!M R
(
n
R)
,得证.
整函数: 在整个复平面上解析的函数称为整函数.
49
1
0 1
z100 k 1 z 2k
98!!
§2.5 解析函数的高阶导数
1.高阶导数
2. 柯西不等式与刘维尔定理
柯西不等式:设f (z)在区域B上解析,为B内一点,以
为圆心作圆周: R,只要及其所包含区域均含于
B, 则有
f
(n) ( )
n!M (R) Rn
0 2i 2i 0 0
即
C
1 z2
z
dz
0
§2.3 不定积分
证:
B
§2.4 柯西公式
1.有界区域柯西公式
( )
证: 如图,根据复连通区域柯西定理有
1 f (z)
1 f (z)
dz
dz
2i C z
2i Cr z
欲证原式,即证
第二章 复变积分
§2.1 复变积分
性质:
例:
补:简单曲线 光滑曲线
1. 简单曲线
设曲线C的参数方程为 x x(t), y y(t), z z(t) (a t b)
其中,x(t), y(t), z(t)在[a, b]连续,当t1 t2 (a t1, t2 b)时, (x(t1), y(t1), z(t1)) (x(t2 ), y(t2 ), z(t2 ))
20复变函数积分

这里dS表示弧长的微分,即 dS (dx)2 (dy)2
1. 通过定义计算
f (z)dz
L
2. 通过计算实线积分来计算
f (z)dz f (z)dz
L1
L1
C f (z)dz C (udx vdy) iC (vdx udy)
例1求 Re zdz ,C为 C
(2)曲线段的方向:规定曲线段的方向为从起点到 终点。
定义:复变积分是复数平面上的线积分 设C是复平面上的曲线,函数f(z)在C上有定义。将曲
线C任意分割为n段,分点为z0=A,z1,z2,…,zn=B,ζk 是zk-1 → zk段上的任意一点,作和数
n
f ( k )(zk zk1)
k 1
推论
若f(z)在单连通区域D中解析,则复变积分 f (z)dz
与路径无关。
C
f (z)dz f (z)dz f (z)dz
L
L1
L2
f (z)dz f (z)dz
L
L
l f (z)dz 0
f (z)dz f (z)dz f (z)dz f (z)dz 0
或者,更一般地
C (z a)n dz 20,i,
n 1,且C内含有z a 其他情形
例6:设z0为围线C内部一点,n为整数,则
C
dz (z z0 )n
20,in, n11
P20: 1. 3.
C
闭合围道C有
C f (z)dz 0
这里C也可以是D的边 界
D
注:Cauchy定理被人们称为解析函数的基本定理
Cauchy定理从一个侧面反映了解析函数的一个基本特 性:解析函数在它的解析区域内,各点的函数值是 密切相关的
1. 通过定义计算
f (z)dz
L
2. 通过计算实线积分来计算
f (z)dz f (z)dz
L1
L1
C f (z)dz C (udx vdy) iC (vdx udy)
例1求 Re zdz ,C为 C
(2)曲线段的方向:规定曲线段的方向为从起点到 终点。
定义:复变积分是复数平面上的线积分 设C是复平面上的曲线,函数f(z)在C上有定义。将曲
线C任意分割为n段,分点为z0=A,z1,z2,…,zn=B,ζk 是zk-1 → zk段上的任意一点,作和数
n
f ( k )(zk zk1)
k 1
推论
若f(z)在单连通区域D中解析,则复变积分 f (z)dz
与路径无关。
C
f (z)dz f (z)dz f (z)dz
L
L1
L2
f (z)dz f (z)dz
L
L
l f (z)dz 0
f (z)dz f (z)dz f (z)dz f (z)dz 0
或者,更一般地
C (z a)n dz 20,i,
n 1,且C内含有z a 其他情形
例6:设z0为围线C内部一点,n为整数,则
C
dz (z z0 )n
20,in, n11
P20: 1. 3.
C
闭合围道C有
C f (z)dz 0
这里C也可以是D的边 界
D
注:Cauchy定理被人们称为解析函数的基本定理
Cauchy定理从一个侧面反映了解析函数的一个基本特 性:解析函数在它的解析区域内,各点的函数值是 密切相关的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
推论1 若f(z)在闭单通区域 中解析,则 f(z)沿 的边界L的积分为零.
证明 按定义, f(z)在包含 的某个开区域D+内 解析,这样 的边界线L就是D +内部的一条 闭曲线.根据柯西定定理可知, f(z)沿L的积分 为零
(2.2.5)
22
推论2 若f(z)在单通区域D内解析,则 ∫l f(z)dz 与路径无关。
C-R条件: 在解析点, f(z)的实部与虚部取值的 关联性;
§2.2.1 单通区域的柯西定理
定理 若函数f(z)在单通区域D 内解析,则f(z)在D内沿任意 闭曲线的积分为零
∮l f(z)dz = 0 (2.2.1)
证明 这个定理的严格证明比较复 杂, 为简单起见, 我们在“f(z)在D内 连续” 附加条件下证明这个定理.
2
§2.1.2 复变积分的计算方法
(1) 化为两个实变线积分计算. 将 f(z) = u+iv 及 dz = dx+idy 代入,即有
(2.1.3)
(2) 化为参数积分计算.设积分曲线L的参数方程为z(t),
将z(t)及dz(t)=z'(t)dt代入式(2.1.4),可得
3
【例2.1.1】计算积分I=
其中曲线L是
(1)沿1+ i 到2+4 i 的直线,见图2.2(a);
(2)沿1+ i 到2+i,再到2+4 i 的折线,见图2.2(b) ;
(3)沿抛物线x=t, y=t2,其中1≤ t ≤2,见图2.2(c) .
4
解 (1) 直线方程为 先将 z=x+iy 代入被积表达式,
随后将 y=3x-2 代入,即有
先将复变积分化为两个实变积 分的线性叠加
(2.2.2)
20
其次, 考查上述两个实变积分在什么条件下为零?
设l为D内任一闭曲线(图2.5), 若函数P(x,y),
Q(x,y) 以及
在D内连续,则格林公式
成立
由f(z)在 D内解析及 f’(z)在D内连续可得u,v
及ux,uy,vz,vy连续,将格林公式与C-R条件 代入式(2.2.2),可得
则f(z)沿图2.3中无穷大半圆周CR的积分
证明 式(2.1.16)中的 积分是一个复数,只 要证明,当R→∞时这 个复数的模为零,则 式(2.1.16)得证.
12
根据复变积分性质(5)及式(2.1.15),易得
13
【2.1.3】试证明 若当(Jordan)不等式
证明 分别作出
y1=2q/p 及
数学物理方法第2章复变函 数积分2020
§2.1.1 复变函数积分的定义
设L为复平面上的曲线,函 数f(z)在L上有定义,将曲
线L任意分成n段,xk是第k 段[zk-1,zk]上的任一点
.令n→∞,且每一段的长 度|Dz|→0时,若和式的极 限
存在,且与弧段的分法及各xk的选取无关,则称此
极限为f(z)沿曲线L的积分,记作
证明 设A、B分别为两积分 曲线的起点和终点,如图2.6 所示.
因为l1,与l2- (l2- 与l2重合但反 向)构成闭曲线l,由柯西定 理可得
(2.2.6)
移项,利用复变积分的性质(2),即有
(2.2.7)
23
§2.2.2 原函ຫໍສະໝຸດ 与定积分公式既然单通区域中解析函数的积分与路径无关, 设积分路径的起点为定点z0,终点为动点z, 则 积分上限的函数 (2.2.8)
y2 = sinq 的函数 曲线图(图2.4). 易见在开区间 (0,p/2)中,有
sinq >2q/p ; 而在闭区间[0,p/2 ]的端点,有sinq = 2q/p。
14
【2.1.4】试证明 若当引理:若z在上半平 面及实轴上趋于∞时,f(z)一致地趋于零( 与辐角无关),则
式中m>0,CR是以原点 为圆心、R为半径的上 半圆周,参看图2.3.
是单通区域内的单值函数,现在证明它是f (z) 的原函数.
24
定理 若f(z)是单通区域D内的解析函数,则
也是D内的解析函数,且
证明 由 先计算
F(z+Dz)-F(z)。利用
式(2.2.8)及复变积分 的性质(1),可得
25
由于解析函数的积分与路径无
积分的许多性质是实变积分的直接推广。对 于这些性质,我们将不加证明地叙述.
(1)若曲线L依次由n段线段l1, l2,… ln组成,则
(2)掉转积分路径的方向,积分变号,即
式中l-与l重合,但方向相反
8
(3) 若f1(z)与f2(z)沿L的积分存在,则
(2.1.10) 上式还可推广为有限多项函数和、差的情形. (4) 被积函数中的任意复常数a 可提出积分号外 ,即
9
(5) 复变积分的模不大于被积函数的模沿曲线 的实变线积分,即
证明由实变函数线积分的定义出发,并利用“ 矢量之和的长度不大于矢量长度之和” ,以 及复变积分的定义,即有
10
(6)若在曲线 l 上, max|f(z)|=M, 曲线 l 的长度为
l ,则
11
【2.1.2】试证明,若z在上半平面及实轴上趋 于∞时, zf(z)一致地趋于零(与辐角无关),即
由复变积分性质(5)导出的例2.1.2和例2.1.4这 两个结论,将会启发我们怎样用留数定理计 算实变积分,见4.2节.
对于解析函数的积分,还具有一些特有的性 质,由2.2节、2.3节介绍的柯西定理、柯西公 式、最大模定理等反映.
18
§2.2 解析函数的柯西定理 原函数与定积分公式
柯西定理:解析函数积分理论的基本定理,从 积分的角度给出解析函数在其解析 区域取值的关联性.
15
证明 当z 在CR上时,z=Reiq,由复变积
分性质(5)可得
将积分(2.1.19)分为两项: 0由p/2的积分与由p/2 到p的积分.第二项先作变换 q = p-j,再用q 表示j,两项合并后利用若当不等式,即有
16
17
综合式(2.1.20)和式(2.1.19)式,并利用题设条件
(2.1.21)
5
(2) 在1+i到2+i段 有 y=1,dy=o
;在2+i到2+4i段 有 x=2,
dx=0,因而
6
(3) 将z=x+iy=t(1+it)及dz=(1+i2t)dt 代入,即有
x=t, y=t2
本题沿三个不同路径的积分值相同,但是“积 分与路径无关”这个结果不是必然的.
7
§2.1.3 复变积分的性质 既然复变积分可归结为实变积分,因此,复变
