一二次函数
一元二次函数的解法

一元二次函数的解法函数定义了一个点集中的每个点的坐标关系,其中一元二次函数是最常用的函数之一,它可以描述许多实际中出现的应用。
一元二次函数的定义是:函数y=ax2+bx+c(a≠0),其中a、b、c是实数,称为一元二次函数。
一元二次函数的特点是它可以根据函数图像分析出它的特征,例如,对于一元二次函数图像,可以分析出它的顶点坐标、凹凸性和函数一阶导数的符号以及二阶导数的符号等。
一元二次函数的求解方法也有多种,例如,可以采用直接法、差商法和因式分解法等。
1、直接法直接法是指通过求解方程,直接求解函数的值。
例如,一元二次函数y=ax2+bx+c,将其化为一元二次方程ax2+bx+c=0,可以使用两个不等式相减或方程根定理求解该一元二次方程。
2、差商法差商法是通过求解指定的函数的差商来求解的。
例如,一元二次函数y=ax2+bx+c,可以求解两个不同点(x1,y1)、(x2,y2)处的三阶差商和四阶差商,从而求解出该函数的系数a、b、c的值。
3、因式分解法因式分解法是通过求解一元二次函数的因式展开式,求解出该函数系数a、b、c的值。
例如,一元二次函数y=ax2+bx+c,可以将它分解成(x+α)(x+β)=0的形式,然后给出α,β的值,从而求得该函数的系数a、b、c。
4、特例求解法特例求解法是指利用某些特殊的情况来直接求解一元二次函数的,例如当一元二次函数的b=0时,可以直接求解出它的系数a、b、c的值。
以上就是一元二次函数的求解方法和分析,一元二次函数的研究和分析有着重要的实际意义,它可以应用于工程设计、投资管理、金融预测等等。
有了对一元二次函数的准确掌握,就可实现精准的计算。
总之,一元二次函数是一种非常常用的函数,它可以应用于各种实际工程领域的计算和分析,掌握其一元二次函数的求解方法既有利于开展理论研究,又有利于实际工程中的应用。
一元二次函数归纳

一元二次函数的图象一、 定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的一元二次函数. 其中,x 是自变量,a,b,c 分别是函数表达式的二次项系数、一次项系数和常数项。
二、一元二次函数y =ax ²+bx +c ﹙a ≠0﹚的图象(其中a,b,c 均为常数)1.当a >0时 函数图象开口向上;对称轴为x =﹣2a /b ,有最小值且为﹙4ac -b ²﹚/4a ; 当x ∈﹙﹣∞,﹣2a /b]时递减;当x ∈[﹣2a /b,﹢∞﹚时递增;2.当a <0时函数图象开口向下;对称轴为x =﹣2a /b ,有最大值且为﹙4ac -b ²﹚/4a ; 当x ∈﹙﹣∞,﹣2a /b]时递增;当x ∈[﹣2a /b,﹢∞﹚时递减;2.△=b ²-4ac当△>0时,函数图象与x 轴有两个交点; 当△=0时,函数图象与x 轴只有一个交点; 当△<0时,函数图象与x 轴没有交点。
(如下图所示)三、抛物线c bx ax y ++=2中,c b a ,,的作用(1) a 决定开口方向及开口大小,这与2ax y =中的a 完全一样.例1:画出212y x =- 2y x =- 22y x =-的图象212y x =- 22y x =- 2y x =-归纳:一般地,抛物线2y ax =的对称轴是y 轴,顶点是原点,当0a >时,抛物线的开口向上,顶点是抛物线的最低点,a 越大,抛物线的开口越小;当0a <时,抛物线的开口向下,顶点是抛物线的最高点,a 越大,抛物线的开口越大。
(2)b 和a共同决定抛物线对称轴的位置例2:画出二次函数21(1)2y x =-+,211)2y x =--(的图象,考虑他们的开口方向、对称轴和顶点。
21(1)2y x =-+ 211)2y x =--(可以看出,抛物线21(1)2y x =-+的开口向下,对称轴是进过点(-1,0)且与x 轴垂直的直线,记为x=-1,顶点是(-1,0);抛物线211)2y x =--(的开口向下,对称轴是x=1,顶点是(1,0)。
关于一元二次函数,一元二次方程,一元二次不等式及其关系

1. 一元二次函数函数 2y ax bx c =++ (0)a ¹叫做一元二次函数,其中,,a b c 是常数 一般式2y ax bx c =++ ( 0a ¹)顶点式 ()2y a x h k =-+ (0a ¹),其中(),h k 为抛物线顶点坐标两点式()()12y a x x x x =-- ( 0a ¹), 其中12,x x 是抛物线与x 轴交点的横坐标。
1.1一元二次函数的基本性质1.1.1一元二次函数的定义域和值域 一元二次函数2y ax bx c =++ ,(0)a ¹的R一元二次函数2y ax bx c =++ ,(0)a ¹ 的值域是0a >时一元二次函数的值域是24,4ac ba 轹-÷ê÷+ ÷ê÷øë 0a <时一元二次函数的值域是24,4acb a 纟-çú- ççúèû1.1.2一元二次函数的单调性1. 2y ax bx c =++ , ()0a > 在区间,2ba 纟çú-?ççúèû上为单调减函数 ,在区间,2ba 轹÷ê-+ ÷÷êøë上为单调增函数 。
当2b x a=-时 2min 44ac b y a-=, m ax y =无2. 2y ax bx c =++ ()0a <在区间,2ba 纟çú-?ççúèû上为单调增加函数,在区间,2ba轹÷ê-+ ÷÷êøë上为单调减函数 。
一元二次方程定义

一元二次方程定义一元二次方程是一种形如 $ax^2+bx+c=0$ 的代数式,其中 $a,b,c$ 都是实数且 $a \e 0$。
在数学中,一元二次方程是一类基本的二次函数,它在数学上的应用广泛,尤其在物理学、工程学、计算机科学等领域中,有着重要的作用。
一元二次方程的参数$a,b,c$ 分别代表二次项系数、一次项系数和常数项。
在解一元二次方程时,我们的主要任务就是求解方程的根。
通常来说,有三种常见的解法,即因式分解法、求根公式法和配方法。
不过,这三种方法并不一定适用于所有的一元二次方程。
在接下来中,我们将具体介绍这三种解法以及它们的应用场景。
1. 因式分解法因式分解法是最为直观的解法之一。
对于形如 $ax^2+bx+c=0$ 的一元二次方程,如果其二次项系数 $a$ 不为零并且其方程左边的多项式是可因式分解的,那么我们就可以使用因式分解法来解方程。
具体步骤如下:(1)观察方程左边的多项式,尝试将其因式分解为两个一次多项式的乘积,即 $ax^2+bx+c=(mx+p)(nx+q)$。
(2)将因式分解后的乘积式展开并合并同类项,得到一个新的二次方程,即 $mnx^2+(mq+np)x+pq=0$。
(3)将新的二次方程与原方程进行比较,即可得到各个系数的关系,从而求出方程的根。
需要注意的是,因式分解法并不适用于所有的一元二次方程。
具体来说,它只适用于一元二次方程的方程左边的多项式可以被分解为两个一次多项式的乘积的情况。
如果方程左边的多项式是一个完全平方式,则我们可以直接使用求根公式法来求解。
2. 求根公式法求根公式法是解一元二次方程时最为常见的一种方法。
它基于一种著名的求根公式,即 $x=\\frac{-b\\pm \\sqrt{b^2-4ac}}{2a}$。
这个公式也被称为一元二次方程的通项公式。
在使用求根公式法时,我们需要依次求出二次项系数 $a$、一次项系数$b$ 和常数项 $c$ 的值,并将其代入求根公式中即可求解方程的根。
一元二次函数
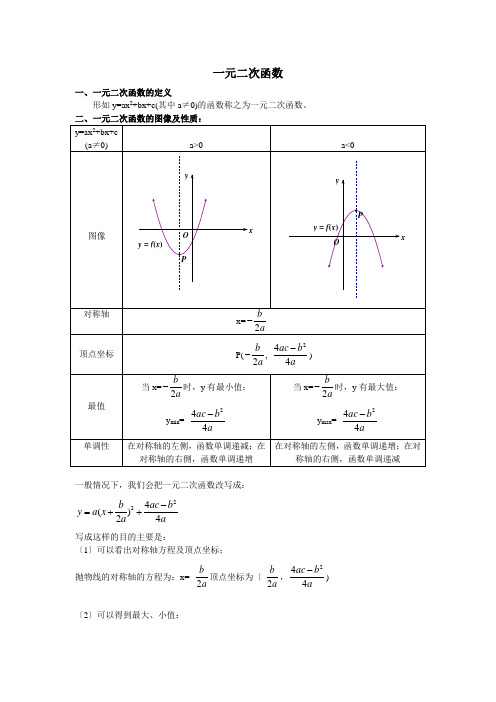
一元二次函数一、一元二次函数的定义形如y=ax 2+bx+c(其中a ≠0)的函数称之为一元二次函数。
一般情况下,我们会把一元二次函数改写成:224()24b ac b y a x a a-=++写成这样的目的主要是:〔1〕可以看出对称轴方程及顶点坐标;抛物线的对称轴的方程为:x= -2b a 顶点坐标为〔-2b a ,244ac b a-)〔2〕可以得到最大、小值:当a >0,y 取最小值,y= 244ac b a-当a<0,y 取最大值,y= 244ac b a-由一元二次函数的对称轴,从而我们可以知道一元二次函数的单调性:当a>0时,〔-∞,-2b a ]为单调减区间;[-2b a ,+∞〕为单调增区间。
当a<0时,[-2b a ,+∞〕为单调减区间;〔-∞,-2ba]为单调增区间〔3〕解答平移问题方便。
平移的法那么遵循两条:左加右减,上加下减。
题型一:平移图像,求新的解析式 【例题1】:y=x 2-2x+3向左移动一个单位,向上移动两个单位,移动后的解析式是什么? 解答:y=(x-1)2+2根据“左加右减〞的原那么,向左移动一个单位,那么有:y=(x-1+1)2+2 根据“上加下减〞的原那么,向上移动两个单位,那么有y=(x-1+1)2+2+2 所以,最终的结果是:y=x 2+4题型二:三点求函数的解析式——方法:待定系数法【例题2】一元二次方程y=ax 2+bx+c 经过点A(1,3),B(2,4),C(3,11),求函数的解析式。
解答:根据题意有:a b c 34a 2b c 49a 3b c 11++=⎧⎪++=⎨⎪++=⎩解上面的方程组,得:388a b c =⎧⎪=-⎨⎪=⎩所以:y=3x 2-8x+8【例题3】函数y=ax 2+bx+c 与x 轴的交点为A(-3,0),B(1,0),并且经过点〔4,21〕,求函数的解析式。
一般情况下,如果告诉你一元二次方程的两个解x 1,x 2;这个时候我们设:y=a(x-x 1)(x-x 2)最为方便。
一元二次函数配方法

一元二次函数配方法一元二次函数是指具有形式为f(x) = ax^2 + bx + c的函数,其中a、b、c为常数且a不为零。
一元二次函数的配方法是指通过变形将一元二次函数转化为完全平方的形式,从而方便求解函数的最值、根、顶点等性质。
一元二次函数的配方法是学习高中数学中非常重要的一个知识点,掌握好配方法对于理解和应用一元二次函数具有重要意义。
首先,我们来了解一元二次函数的标准形式及完全平方形式。
一元二次函数的标准形式为f(x) = ax^2 + bx + c,其中a、b、c为常数且a 不为零。
完全平方形式即为将一元二次函数重新排列写成一个平方式的样子。
一般来说,将一元二次函数f(x) = ax^2 + bx + c变形为完全平方形式,即将它写成一次平方项的和,即f(x) = a(x - h)^2 + k。
其中(h, k)就是函数的顶点坐标。
下面我们来讲解一下一元二次函数的配方法。
首先,对于一元二次函数f(x) = ax^2 + bx + c,我们要先找到a、b两项的系数,然后进行配方法变形成完全平方形式。
如何变形呢?我们以一些例子来说明:例子1:将函数f(x) = x^2 + 4x + 3变形为完全平方形式。
首先,我们找到a、b的系数分别为1和4。
然后,我们将b项的系数4折半,得到2,然后加上一个平方的常数项,即+2^2 = 4。
注意,我们要保持等式的平衡,所以我们加4之后要减去4,这样才不改变原式。
于是,我们得到f(x) = (x + 2)^2 - 1。
这样,我们就将一元二次函数变形成了完全平方形式。
从而可以方便求得函数的最值、根、顶点等性质。
例子2:将函数f(x) = 2x^2 + 8x + 5变形为完全平方形式。
首先,找到a、b的系数分别为2和8。
然后,以与例子1相同的方法,我们将b项的系数8折半,得到4,然后加上一个平方的常数项,即+4^2 = 16。
于是,我们得到f(x) = 2(x + 4)^2 - 11。
一元二次方程概念

3
因数分解法
适用于形如ax²+ bx + c = 0,其中a = 1或a不等于1,可以通过因式分解法去解。
一元二次方程的图像
一次函数的图像
二次函数的图像
一次函数的图像是一条直线,斜率代表了直线的倾 斜程度和函数的增长速度。
二次函数的图像是一条开口朝上或朝下的抛物线, 顶点处为极值点。
一元二次方程的性质
1 判别式
判别式D = b²-4ac常用于判断一元二次方程的解的情况。
2 轨迹离散
当二次项系数a的值越小或越大时,抛物线的轨迹越趋向于x轴或y轴。
3 图像对称
抛物线关于顶点对称。
一元二次方程的应用
物理应用
抛物线的底部宽度可以应用于建 筑设计、设计跃高运动场地等需 要计算物体的轨迹的场合。
商业应用
二次函数的相关参数可以用于广 告投入和销售额的关系,以及生 产成本和产量的关系等商务领域 的计算。
我们为什么要学习一元二次方程?
研究一元二次方程有助于我们更深入地了解二次函数的基本概念
一元二次方程的一般形式
标准形式
一元二次方程的一般形式为:ax² + bx + c = 0,其中a、b、c是已知 常数,x是未知变量。
无解情况
当b²-4ac小于0时,一元二次方程 没有实数根,称为无解情况。
解的总数
一元二次方程的应用?ຫໍສະໝຸດ 物理、商务和科学领域广泛 使用了一元二次方程的相关 数学概念。
一元二次方程有0、1或2个解。 具体解的数量取决于求方程的解 时一次项系数的符号和二次项系 数与常数项之间的关系。
一元二次方程的解的求法
1
配方法
适用于ax²+ bx + c = 0,通过配方将一元二次方程变为完全平方。
二次函数及一元二次不等式

一、一元二次函数及一元二次不等式一、二次函数1.函数)0(2≠++=a c bx ax y 叫做一元二次函数。
2. 一元二次函数的图象是一条抛物线。
3.任何一个二次函数)0(2≠++=a c bx ax y 都可把它的解析式配方为顶点式:ab ac ab x a y 44)2(22-++=,性质如下:(1)图象的顶点坐标为)44,2(2ab ac ab --,对称轴是直线ab x 2-=。
(2)最大(小)值① 当0>a ,函数图象开口向上,y 有最小值,a b ac y 442min -=,无最大值。
② 当0<a ,函数图象开口向下,y 有最大值,ab ac y 442max -=,无最小值。
(3)当0>a ,函数在区间)2,(ab --∞上是减函数,在),2(+∞-ab上是增函数。
当0<a ,函数在区间上),2(+∞-a b 是减函数,在)2,(ab --∞上是增函数。
【例1】求作函数64212++=x x y 的图象【解】 )128(21642122++=++=x x x x y【练习1】(1)求作函数362++=x x y 的图象。
(2)求作函数342+--=x x y 的图像【解】)34(3422-+-=+--=x x x x y 7)2[(]7)2[(22++-=-+-=x x (二)一元二次函数性质【例2】求函数962++=x x y 的最小值及图象的对称轴和顶点坐标,并求它的单调区间。
【解】 7)3(79626222-+=-++=++=x x x x x y 由配方结果可知:顶点坐标为)73(--,,对称轴为3-=x ; 01> ∴当3-=x 时, 7min -=y 函数在区间]3(--∞,上是减函数,在区间)3[∞+-,上是增函数。
【练习2】求函数1352++-=x x y 图象的顶点坐标、对称轴、最值及它的单调区间。
103)5(232=-⨯-=-ab ,2029)5(431)5(44422=-⨯-⨯-⨯=-ab ac∴函数图象的顶点坐标为)2029,103(,对称轴为2029=x05<- ∴当103=x 时,函数取得最大值2029=maz y函数在区间]103,(-∞上是增函数,在区间),3[+∞-上是减函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O y x O x y O y x O x
y B C D
1.函数x
y 1-=的自变量x 的取值范围是 . 2、如图1,所示计算程序中,y 与x 之间的函数关系对应的图象所在象限是( )象限 图1 3、已知反比例函数y =1x
,下列结论不正确...的是( ) A .图象经过点(1,1) B .图象在第一、三象限C .当x >1时,0<y <1 D .当x <0时,y 随着x 的增大而增大
4、如图2,A 是反比例函数图象上一点,过点A 作AB ⊥y 轴于点B ,点P 在x 轴上,△ABP 的面积为
2,则这个反比例函数的解析式为______________.
5、(2010山东青岛市)函数y ax a =-与a y x =(a ≠0)在同一直角坐标系中的图象可能是( ).
A .
B .
C .
D .
6、二次函数y=ax 2+bx+c 的图像如图3所示,反比例函数y=a x
与正比例函数y=(b+c)x 在同一坐标系中的大致图像可能是( )
图4
7、如图4,在直角坐标系xOy 中,直线l 过(1,3)和(3,1)两点,且与x 轴,y 轴分别交于A ,B 两点.(1)求直线l 的函数关系式;(2)求△AOB 的面积.(本题写过程)
8、如图5,坐标平面内一点A (2,-1),O 为原点,P 是x 轴上的一个动点,如果以点P 、O 、A 为顶点的三角形是等腰三角形,那么符合条件的动点P 的个数为( )
9、如图6,直线1l :1y x =+与直线2l :y mx n =+相交于点P (a ,2),则关于x 的不等式1x +≥mx n +的解集为 .10、(2010年成都)在平面直角坐标系中,点(2,3)A -位于第________象限.
11(2010年眉山)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y (升)与时间x (分)之间的函数关系对应的图象大致为( )
12(北京)如图7,直线y =2x +3与x 轴交于点A ,与y 轴交于点B 。
(1) 求A 、B 两点的坐标; 图7
(2) 过B 点作直线BP 与x 轴交于点P ,且使OP =2OA ,求△ABP 的面积。
(写过程)
13. (上海)已知函数 f ( x ) = 1x 2 + 1
,那么f ( ─ 1 ) = _____ 14、在抛物线y =x 2-4上的一个点是( )(A )(4,4)(B )(1,一4)(C )(2,0)(D )(0,4)
15、抛物线()322
+-=x y 的顶点坐标是( ) 输入x 取倒数 ×(-5) 输出y
O y y O y x O y x O
O 第26题 y ·P x 16、抛物线21323
y x x =-
+-与2y ax =的形状相同,而开口方向相反,则a =( ) 17、与抛物线532
12-+-=x x y 的形状大小开口方向相同,只有位置不同的抛物线是( ) A .2523412-+-=x x y B .87212+--=x x y C .1062
12++=x x y D .532-+-=x x y 4.二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
A .x =4 B. x =3 C. x =-5 D. x =-1。
18、抛物线122+--=m mx x y 的图象过原点,则m 为( )A .0
B .1
C .-1
D .±1
6.把二次函数122--=x x y 配方成顶点式为( )
A .2)1(-=x y
B . 2)1(2--=x y
C .1)1(2++=x y
D .2)1(2-+=x y 19、二次函数c bx ax y ++=2的图象如图所示,则abc ,ac b 42-,b a +2,c b a ++这四个式子
中, 值为正数的有( )A .4个 B .3个 C .2个 D .1个
20、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,给出以下结论
:① 0a b c ++<;② 0a b c -+<;③20b a +<;④0abc >.
其中所有正确结论的序号是( )
A. ③④
B. ②③
C. ①④
D. ①② 21、直角坐标平面上将二次函数y =-2(x -1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
22.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )
A .3<k
B .03≠<k k 且
C .3≤k
D .03≠≤k k 且 23.已知反比例函数x k y =
的图象如右图所示,则二次函数222k x kx y +-=的图象大致为( )
24、若抛物线n m x a y ++=2)(的开口向下,顶点是(1,3),y 随x 的增大而减小,则x 的取值 范围是( )(A )3x > (B )3x < (C )1x > (D)0x <
25、(2010贵州铜仁)定义运算“@”的运算法则为:x@y =xy -1,则(2@3)@4=__ _
26.如上图(26题),已知⊙P 的半径为2,圆心P 在抛物线y =12
x 2—1上运动,当⊙P 与x 轴相切 时,圆心P 的坐标为_________________.
27、某商场欲购进A 、B 两种品牌的饮料500箱,此两种饮料每箱的进价和售价如下表所示。
设购 进A 种饮料x 箱,且所购进的两种饮料能全部卖出,获得的总利润为y 元.
⑴求y 关于x 的函数关系式?
⑵如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能
获利最多?并求出最大利润。
(注:利润=售价-成本) y O x y
O x y O x y O x y O x O x
y -1。
