牛顿插值法试验报告
数值分析实验报告-插值、三次样条
实验报告：牛顿差值多项式&三次样条问题：在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值，对每个n 值，分别画出插值函数及()f x 的图形。
实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求：1． 认真分析问题，深刻理解相关理论知识并能熟练应用；2． 编写相关程序并进行实验；3． 调试程序，得到最终结果；4． 分析解释实验结果；5． 按照要求完成实验报告。
实验原理：详见《数值分析 第5版》第二章相关内容。
实验内容：（1）牛顿插值多项式1.1 当n=10时：在Matlab 下编写代码完成计算和画图。
结果如下：代码：clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p ;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式，其结果为：P10（x）=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.1）。
牛顿插值法实验报告
牛顿插值法实验报告篇一：牛顿插值法实验报告牛顿插值法一、实验目的：学会牛顿插值法，并应用算法于实际问题。
二、实验内容：给定函数f?x，已知：f?? f?f??三、实验要求：（1）用牛顿插值法求4次Newton 插值多项式在处的值，以此作为函数的近似值?N。
在MATLAB中用内部函数ezplot绘制出4次Newton插值多项式的函数图形。
（2）在MATLAB中用内部函数ezplot可直接绘制出以上函数的图形，并与作出的4次Newton插值多项式的图形进行比较。
四、实验过程：1、编写主函数。
打开Editor编辑器，输入Newton插值法主程序语句：function [y,L]=newdscgn=length; z=x; A=zeros;A=Y’;s=; p=;for j=2:nfor i=j:nA=- A)/-X);endendC=A;for k=:-1:1C=conv));d=length;C=C+A;endy= polyval;L=poly2sym;%%%%%%%%%%%%%%%%%%t=[2,,,,];fx=sqrt;wucha=fx-Y;以文件名保存。
2、运行程序。
（1）在MATLAB命令窗口输入：>> X=[2,,,,]; Y=[,,,,];x=;[y,P]=newdscg回车得到：y =wucha = *-P = - /2305843009213693952 +/288230376151711744 -/1125899906842624 +/2251799813685248 + 1865116246031207/4503599627370496（2）在MATLAB命令窗口输入：>> v=[0,6,-1,3];>> ezplot,axis,grid>> hold on>> x=0::6;>> yt=sqrt;plot>> legend>> xlabel>> ylabel>>title回车即可得到图像1-1。
插值法实验报告
插值法实验报告插值法实验报告一、引言插值法是一种常用的数值分析方法，用于通过已知数据点的函数值来估计在其他位置的函数值。
它在科学计算、图像处理、工程设计等领域有广泛的应用。
本实验旨在通过实际操作，深入理解插值法的原理和应用。
二、实验目的1. 掌握拉格朗日插值法和牛顿插值法的原理和计算方法；2. 通过实验比较不同插值方法的精度和效率；3. 分析插值法在实际问题中的应用。
三、实验步骤1. 收集实验数据：在实验室内设置几个测量点，记录它们的坐标和对应的函数值；2. 使用拉格朗日插值法计算其他位置的函数值：根据已知数据点，利用拉格朗日插值公式计算其他位置的函数值；3. 使用牛顿插值法计算其他位置的函数值：根据已知数据点，利用牛顿插值公式计算其他位置的函数值；4. 比较不同插值方法的精度和效率：通过计算误差和运行时间，比较拉格朗日插值法和牛顿插值法的性能差异；5. 分析插值法在实际问题中的应用：结合实验结果，探讨插值法在实际问题中的优势和局限性。
四、实验结果与分析1. 拉格朗日插值法的计算结果：根据已知数据点，利用拉格朗日插值公式计算其他位置的函数值；2. 牛顿插值法的计算结果：根据已知数据点，利用牛顿插值公式计算其他位置的函数值；3. 误差分析：比较插值结果与真实函数值之间的误差，分析误差的来源和影响因素；4. 运行时间分析：比较不同插值方法的运行时间，分析其效率和适用场景。
五、实验结论1. 拉格朗日插值法和牛顿插值法都是常用的插值方法，它们在不同场景下有各自的优势；2. 插值法在实际问题中的应用需要考虑数据的分布、函数的性质和计算效率等因素；3. 本实验结果表明，拉格朗日插值法和牛顿插值法在精度和效率上存在差异，具体选择哪种方法应根据实际需求进行权衡。
六、实验总结通过本次实验，我们深入了解了插值法的原理和应用。
实验结果表明，插值法在科学计算和工程设计中具有重要的作用。
在实际应用中，我们需要根据具体问题的要求和数据的特点选择合适的插值方法，以达到更好的效果。
newton插值法实验报告
竭诚为您提供优质文档/双击可除newton插值法实验报告篇一：牛顿插值法matlab程序《计算方法》数值实验报告篇二：数值分析实验报告(插值法)武汉理工大学学生实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导老师姓名学生姓名学生专业班级20XX—20XX学年第一学期实验课程名称：数值分析篇三：c++实现牛顿插值法实验报告数值实验用newton商差公式进行插值姓名：陈辉学号：13349006院系：数据科学与计算机学院专业：计算机科学与技术班级：计科一班日期：20XX-10-11指导老师：纪庆革目录一、二、三、四、五、六、七、八、实验目的................................................. .........................................3实验题目................................................. .........................................3实验原理与基础理论................................................. .......................3实验内容................................................. .........................................6实验结果................................................. .......................................10心得体会................................................. .......................................14参考资料................................................. .......................................14附录（源代码）............................................... (14)一、实验目的编写一个程序，用牛顿差商公式进行插值。
不等距节点下的牛顿插值公式以及拉格朗日插值公式实验课报告
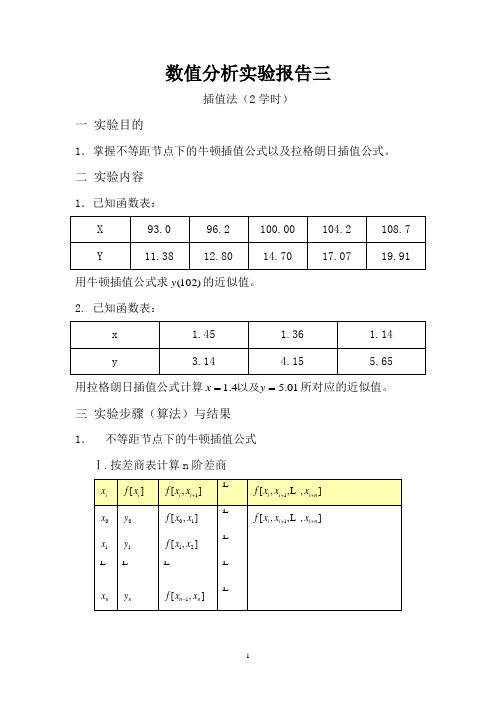
数值分析实验报告三插值法（2学时）一实验目的1．掌握不等距节点下的牛顿插值公式以及拉格朗日插值公式。
二实验内容1．已知函数表：用牛顿插值公式求)(y的近似值。
1022. 已知函数表：用拉格朗日插值公式计算01x以及所对应的近似值。
=y.54.1=三实验步骤（算法）与结果1．不等距节点下的牛顿插值公式Ⅰ.按差商表计算n阶差商12111[,,,][,,,][,,,]i i i n i i i n i i i n i n if x x x f x x x f x x x x x +++++-+++-=- 其中Ⅱ.按以下公式，带入x 值00010120101101()()()[,]()()[,,]()()()[,,]n n f x f x x x f x x x x x x x f x x x x x x x x x f x x -=+-+--++---Ⅲ.得出结果()f x程序代码：#include"stdio.h"#include"math.h" int main() {int a,i,j;printf("输入x 系数的个数："); scanf("%d",&a); float d,e=0,c; float x[a];float y[a-1][a];printf("输入x 的系数："); for(i=0;i<a;i++) {scanf("%f",&x[i]); }printf("输入y 的系数："); for(i=0;i<a;i++) {scanf("%f",&y[0][i]); }for(i=0;i<a;i++) {printf("%1.6f ",x[i]); }printf("\n");for(i=0;i<a;i++){printf("%1.6f ",y[0][i]);}for(j=1;j<a;j++){for(i=0;i<a-j;i++){y[j][i]=(y[j-1][i+1]-y[j-1][i])/(x[j+i]-x[i]);}}printf("\n");for(j=1;j<a;j++){for(i=0;i<a-j;i++){printf("%1.6f ",y[j][i]);}printf("\n");}printf("输入x的值：");scanf("%f",&c);for(j=1;j<a;j++){d=1;for(i=0;i<j;i++){d=d*(c-x[i]);}e=e+d*y[j][0];}e=e+y[0][0];printf("%1.6f",e);return 0;}运算结果：15.7936292．拉格朗日插值公式120010200110110111201()()()()()()()()()()()()()()()()()()()()()()()()()n n i i n i i i i i i i n n n n n n n x x x x x x f x f x x x x x x x x x x x x x x x f x x x x x x x x x x x x x x x f x x x x x x x R x -+-+-----=---+----+-------+---+0101()()()()[,,,,]n n n R x x x x x x x f x x x x =--- 其中余式程序代码：#include"stdio.h" #include"math.h" int main() {int a,i,j;printf("输入x系数（y的系数）的个数：");scanf("%d",&a);float e,k=1,p=0;float x[a];float y[a];printf("输入x的系数（y的系数）：");for(i=0;i<a;i++){scanf("%f",&x[i]);}printf("输入y的系数（x的系数）：");for(i=0;i<a;i++){scanf("%f",&y[i]);}printf("输入你要求的值：");scanf("%f",&e);for(j=0;j<a;j++){k=1;for(i=0;i<a;i++){if(i==j){k=k;}else{k=k*((e-x[i])/(x[j]-x[i]));}}k=k*y[j];p=p+k;}printf("%f",p);return 0;}运算结果：x=1.4时，y=3.729525y=5.01时，x=1.246488四实验收获与教师评语实验收获：对于一系列的x值和对应的y值，有时其数学解析式是未知的，此时可以应用插值法进行插值计算，这是一个重要的数学工具。
FORTRAN实验报告——牛顿插值
IV / 4
s(s+1) 2! s(s −1) 2!
∆2 f0 + ⋯ +
s s −1 …(s −n+1) n!
∆n f0
∇2 fN + ⋯ +
s s+1 …(s+n −1) n!
∇n fN
ERROR 0.0000009 ERROR 0.0000023
c++实现牛顿插值法实验报告概论
数值实验用Newton商差公式进行插值姓名：陈辉学号：13349006院系：数据科学与计算机学院专业：计算机科学与技术班级：计科一班日期：2015-10-11指导老师：纪庆革目录一、实验目的 (3)二、实验题目 (3)三、实验原理与基础理论 (3)四、实验内容 (6)五、实验结果 (10)六、心得体会 (14)七、参考资料 (14)八、附录（源代码） (14)一、实验目的编写一个程序，用牛顿差商公式进行插值。
二、实验题目编写一个程序，用牛顿差商公式进行插值。
三、实验原理与基础理论牛顿插值公式为：N n(x)=f(x0)+f[x0,x1](x−x0)+⋯+f[x0,…,x n](x−x0)…(x−x n−1)其中，f[x0,x1]=f(x1)−f(x0)x1−x0f[x0,…,x k]=f[x1,…x k]−f[x0,…,x k]k0我们将从键盘读入n阶牛顿插值的n+1个节点(x i,f i),i=0,1,…,n，以此得出牛顿插值多项式。
有了节点，我们只需要求f[x0,…,x k]即可。
我们记f[x m,x m−1,…,x m−k]为t[m][k]，则t[m][k]在差商表表的位置为(m, k)：由f[x0,…,x k]的公式可得t[m][k] = (t[m][k-1] - t[m-1][k-1]) / (x[i] – x[i-j])，直观上来看，表中的某格的差商值可由其左边和左上边的值求得，从而牛顿插值多项式变为N(x) = t[0][0] + t[1][1](x-x[0]) + … + t[n][n](x-x[0])…(x-x[n-1])做到这一步，我们已经可以通过上面的数据计算对于给出的x，f(x)的近似值。
为了更规范地表示，下面我把N(x)变换成标准的降幂多项式N(x) = a[n]x^n + a[n-1]x^(n-1) + … + a[2]x^2 + a[1]x + a[0]。
为了便于运算，不妨先把x-x[i]中的减号换成加号（在最后令y[i]=-x[i]，在令x[i]=y[i]，仍可以得到原本的结果），那么有：(x+x[0])(x+x[1])…(x+x[m−1])m−1=x m+x m−1∑x[i]i=0+x m−2∑x[i[0]]x[i[1]]+⋯0≤i[0]≠i[1]≤m−1+x0∑x[i[0]]x[i[1]]…x[i[m−1]]0≤i[0]≠⋯≠i[m−1]≤m−1为了便于表示，把∑x[i[0]]x[i[1]]…x[i[k−1]]0≤i[0]≠⋯≠i[k]≤m−1记为∑x[k]m那么(x+x[0])(x+x[1])…(x+x[m−1])=x m+x m−1∑x[1]+⋯+x0∑x[m]mm只要把N(x)中的每一项展开然后x次数相同的系数相加就可以得到数组a。
牛顿插值上机报告
x
1.1 1.3 1.6 1.9 2.2 2、给出 f(x)=lnx 的数值表 x 0.4 0.5 lnx -0.916291 -0.693147
f(x)
0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 0.6 -0.510826 0.7 -0.356675 0.8 -0.223144
1
一 实验目的 1.了解并掌握 Newton 插值多项式，根据给定的数值表 ，构造 1，2，3，4 次 Newton 插值多项式, 列出算法并求解。 2.并与 Lagrange 插值多项式比较精度。 实验内容 1、给定数据表, 构造 1，2，3，4 次 Newton 插值多项式， 求 f(1.5)=? 并与 Lagrange 插值多项 式比较精度。
一阶插商 -0.7255585 -0.548946 -0.578612 -0.571521
二阶插商
三阶插商
四阶插商
0.353225 -0.0494433333 -0.5033354166 0.01181833333 0.06806851848 0.5194581228
P n x f x0 f x0 , x1 x x0 f x0 , x1 , x2 x x0 x x1
3
f x0 , x1,
, xn x x0
Hale Waihona Puke x xn1 Rn x f x P n x f x0 , x1 , x2 ,
, xn wn1 x , 其中wn+1 x x x0 x x1
end k k 1; end for k ans 1: 1:1 end resulty resulty y k inputx x k * resulty;
牛顿插值的计算实习报告
一、实习目的通过本次实习，我深入了解了牛顿插值法的基本原理，掌握了其计算方法，并能够熟练运用牛顿插值法解决实际问题。
实习过程中，我结合实际数据，运用牛顿插值法进行计算，分析了插值结果，并对插值方法进行了总结和评价。
二、实习内容1. 牛顿插值法的基本原理牛顿插值法是一种构建插值多项式的方法，通过计算差商（divided differences）来逐步构建插值多项式。
该方法具有较好的计算效率和承袭性，即在添加或删除数据点时，可以基于已有计算结果进行调整，无需完全重新计算。
2. 牛顿插值法的计算步骤（1）初始化差商表，第0列初始化为ypoints。
（2）计算i阶差商，根据差商计算插值多项式。
（3）根据计算出的差商构造最终的插值多项式。
（4）计算x的估计函数值。
3. 实际应用以一组实际数据为例，运用牛顿插值法进行计算。
（1）选取一组已知数据点，计算差商。
（2）根据差商构造牛顿插值多项式。
（3）利用牛顿插值多项式估算未知点的函数值。
三、实习结果与分析1. 插值结果通过对实际数据的计算，牛顿插值法得到了较为准确的插值结果。
与实际值相比，插值值具有较高的精度。
2. 插值误差分析（1）在数据点较少的情况下，牛顿插值法具有较高的精度。
（2）在数据点较多的情况下，牛顿插值法可能会出现误差，但总体上仍具有较高的精度。
（3）插值误差与数据点的分布、差商的计算精度等因素有关。
四、实习总结与评价1. 牛顿插值法是一种有效的插值方法，具有较好的计算效率和承袭性。
2. 在实际应用中，根据数据点的分布和精度要求，选择合适的插值方法。
3. 牛顿插值法在实际应用中具有较高的精度，但在某些情况下可能会出现误差。
4. 在后续的实习中，我将进一步学习其他插值方法，如拉格朗日插值法、样条插值法等，以便在实际问题中灵活运用。
五、实习体会通过本次实习，我对牛顿插值法有了更深入的了解，掌握了其计算方法，并能够将其应用于实际问题。
在实习过程中，我认识到理论知识与实际应用相结合的重要性，以及选择合适的插值方法对于提高计算精度的重要性。
插值数值实验报告(3篇)
第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点，并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是：给定一组数据点，构造一个次数不超过n的多项式，使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是：给定一组数据点，构造一个次数不超过n的多项式，使得该多项式在这些数据点上的函数值与已知数据点的函数值相等，并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法（1）给定一组数据点，如：$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$（2）根据拉格朗日插值公式，构造插值多项式：$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$（3）计算插值多项式在不同点的函数值，并与实际值进行比较。
第7章 实验六牛顿插值
第7章 实验六牛顿插值多项式实验目的：掌握牛顿插值多项式公式，会用牛顿插值多项式公式，明确牛顿插值多项式与拉格朗日插值公式的区别。
7.1 牛顿插值多项式定理7.1 已知1+n 个节点n x x x ,,,10 ，（b x x x a n ≤<<<≤ 10，）及节点对应的函数值)(,),(),(10n x f x f x f 。
则唯一存在一个n 次多项式)(x N n ，具有性质：n j y x f x N jj j n ,,1,0)()( ===该多项式形式为：)())(](,,,[)](,[)()(110100100----++-+=n n n x x x x x x x x x f x x x x f x f x N插值余项)(x R 为：)(],,,,[)()()(110x x x x x f x N x f x R n n n +=-=ω 。
其中010110)()(],[x x x f x f x x f --=，121021210],[],[],,[x x x x f x x f x x x f --=，……，110110],,,[],,[],,,[x x x x x f x x f x x x f n n n n --=- 。
牛顿插值多项式公式的优点是具有承袭性，当给出了n+1点坐标，求出)(x N n 表达式后，再给出一个点坐标),(22++n n y x ，则有插值公式：))(())(](,,,,[)()(1101101n n n n n n x x x x x x x x x x x x f x N x N ----+=-++ 。
牛顿插值源代码：清单7.1function [C,D]=newpoly(X,Y)% 输入：x （节点的向量）, y （节点对应的函数值向量）% 输出：C （是牛顿插值多项式系数向量）, D （是计算差商的矩阵） n=length(X); % 节点的个数 D=zeros(n,n) % n ×n 维的零矩阵D(:,1)=Y' % D 的第一列Y （节点对应的函数值向量）for j=2:n for k=j:nD(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1)); % 计算差商 end end C=D(n,n); for k=(n-1):-1:1C=conv(C,poly(X(k))) % 计算插值多项式的系数 m=length(C); C(m)= C(m)+D(k,k); End7.2 牛顿插值插值多项式例7.1 将区间[-5,5]等分5份、10份，求函数)1(12x y +=的牛顿插值插值多项式，作出函数)1(12x y +=的原图像，观察龙格现象得出什么结果？解：将区间[-5,5]等分5份，由清单7.2可计算出牛顿插值多项式的系数：C=[ 0 0.0019 0 -0.0692 0 0.5673 ]清单7.2clear,clf,hold on X=-5:2:5; Y=1./(1+X.^2); [C,D]=newpoly(X,Y) x=-5:0.01:5; y=polyval(C,x); plot(x,y,X,Y,'.') grid on xp=-5:0.05:5; z=1./(1+xp.^2); plot(xp,z,'r')图7.1 5等份的插值多项式曲线与函数)1(12x y +=的曲线将区间[-5,5]等分10份，由清单7.3可计算出牛顿插值多项式的系数：C =[ -0.0000 0.0000 0.0013 0.0000 -0.0244 -0.00000.1974 0.0000 -0.6742 0.0000 1.0000 ]清单7.3clear,clf,hold onX=[-5 -4 -3 -2 -1 0 1 2 3 4 5];Y=[0.0385,0.0588,0.1,0.2,0.5,1,0.5,0.2,0.1,0.0588,0.0385]; [C,D]=newpoly(X,Y) x=-5:0.01:5; y=polyval(C,x); plot(x,y,X,Y,'--') grid on xp=-5:0.05:5; z=1./(1+xp.^2); plot(xp,z,'r')图7.2 10等份的插值多项式曲线与函数)1(12x y +=的曲线例7.2 基于5个点4,3,2,1,0)),cos(,(=k k k ，构造)cos()(x x f =的差商表，并用它找出4,3,2,1,0=k 的系数k α和4个牛顿插值多项式4,3,2,1),(=k x N k 。
牛顿插值法
牛顿插值法一、实验名称：牛顿插值法二、实验目的：学会牛顿插值法，并应用算法于实际问题。
三、实验内容：给定函数 x x f =)(，已知：414214.1)0.2(=f 449138.1)1.2(=f 483240.1)2.2(=f516575.1)3.2(=f 549193.1)4.2(=f四、实验要求：(1)用牛顿插值法求4次Newton 插值多项式在2.15处的值，以此作为函数的近似值)15.2(15.2N ≈。
在MATLAB 中用内部函数ezplot 绘制出4次Newton 插值多项式的函数图形。
(2)在MATLAB 中用内部函数ezplot 可直接绘制出以上函数的图形，并与作出的4次Newton 插值多项式的图形进行比较。
五、实验编程:输入的量：X 是n+1个节点),(i i y x （i=1,2,…,n+1）横坐标向量，Y 是纵坐标向量，x 是以向量形式输入的m 个插值点，M 在[a,b]上满足M x f n ≤+)()1(.输出的量：向量y 是向量x 处的插值，误差限R ，n 次牛顿插值多项式L 及其系数向量C ，差商的矩阵A.function [y,R,A,C,L]=newdscg(X,Y,x,M)n=length(X); m=length(x);for t=1:mz=x(t); A=zeros(n,n);A(:,1)=Y';s=0.0; p=1.0; q1=1.0; c1=1.0;for j=2:nfor i=j:nA(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));endq1=abs(q1*(z-X(j-1)));c1=c1*j;endC=A(n,n);q1=abs(q1*(z-X(n)));for k=(n-1):-1:1C=conv(C,poly(X(k)));d=length(C);C(d)=C(d)+A(k,k);endy(k)= polyval(C, z);endR=M*q1/c1;L(k,:)=poly2sym(C);在MA TLAB 工作窗口输入程序：>> syms M,X=[2.0,2.1,2.2,2.3,2.4]; Y =[1.414214,1.449138,1.483240,1.516575,1.549193]; x=2.15;[y,R,A,C,P]=newdscg(X,Y ,x,M);ezplot(P);hold onezplot('y=sqrt(x)')运行后输出插值)15.2(f y ≈及其误差限公式R ，四阶牛顿插值多项式P 及其系数向量C ，差商的矩阵A 如下y =1.4663R =(8301034833169303*M)/70835497243044678205440A =1.4142 0 0 0 01.4491 0.3492 0 0 01.4832 0.3410 -0.0411 0 01.5166 0.3334 -0.0383 0.0092 01.5492 0.3262 -0.0359 0.0083 -0.0021C =-0.0021 0.0271 -0.1566 0.7215 0.4141P =- (4803839603609061*x^4)/2305843009213693952 + (7806239355294329*x^3)/288230376151711744 - (176292469178709*x^2)/1125899906842624 + (1624739243112817*x)/2251799813685248 + 1865116246031207/4503599627370496由结果可知，插值4663.1)15.2(=≈f y在MATLAB 中运行后，用内部函数ezplot 绘制出4次Newton 插值多项式的函数图形与x x f =)(的图形如下：-6-4-20246-20-15-10-5xy=sqrt(x)y由程序运行出的结果,即上图可知:用内部函数ezplot 绘制出4次Newton 插值多项式的函数图形和x x f =)(的图形相比较起来，在原点附近，两者的值很接近；而在x=6的值都在2附近，且在x 的正半轴两曲线形状很接近，实现了较好的逼近；从输出的结果图可以知道：4次Newton 插值多项式的函数图形在 0=x 的附近，原函数的斜率比4次Newton 插值多项式的函数的斜率大，即增长速度快；并且先增长后接近平行，而x x f =)(的图形相反，先平行后增长。
数值分析实验报告Newton插值法
用 Newton 插值法计算出 x1=0:0.1:1.2 处的值为表 3-2：
0 0.1 0.2 Pn 1 0.995005 0.980067 x 0.7 0.8 0.9 Pn 0.764843 0.696707 0.62161
x
表 3-2 0.3 0.4 0.955337 0.921061 1 1.1 0.540302 0.453596
对于例 3 要画出图像，则应在上述代码中做出改动：
function [A,Pn] = Newton(X,x) %请输入 2*n 矩阵 X，X 中第一行每个元素都是插值节点，X 中第二行每个元素都是插值节点对应的函 数值； %第二章 P36 例三牛顿插值 n=size(X,2); Pn=zeros(1,size(x,2));%存放插值 t=1;s=size(x,2) for k=1:1:s A=zeros(n,n+1);%存放差商表 A(:,1:2)=X'; if x(1,k)==X(1,t); Pn(1,k)=X(2,t); t=t+1; else for i=3:1:n+1 m=1; for j=i-1:1:n A(j,i)=(A(j,i-1)-A(j-1,i-1))/(A(j,1)-A(m,1)); m=m+1; end
xi
0 0.2 0.4 0.6 0.8 1 1.2
f(xi )
1 0.980067 0.921061 0.825336 0.696707 0.540302 0.362358 -0.09966 -0.29503 -0.47863 -0.64315 -0.78203 -0.88972
i 阶差商
t(•) t(0) t(1)
>> X=[0 0.2 0.4 0.6 0.8 1.0 1.2;1 0.980067 0.921061 0.825336 0.696707 0.540302 0.362358]; >> x=0.3; >> format long >> [A,Pn,B]=Newton1(X,x) Pn = 0.955336593750000 表 3-1 差商表
牛顿插值法实验报告
牛顿插值法实验报告x一、实验目的1. 了解牛顿插值法的理论原理；2. 通过Matlab软件模拟实现牛顿插值法的程序；3. 学习利用牛顿插值方法求解函数在指定单点上的值。
二、实验过程1. 理论推导牛顿插值法是用数值分析的有效的一类插值方法，在一定程度上，可以得到函数的求解结果。
其核心思想是把所求函数拟合成一系列的多项式，以此实现函数的求解。
牛顿插值法可以通过牛顿第二型插值多项式来实现，该多项式的构造方法如下：令n+1个数据点分别为x_0,x_1,…,x_n，对应的函数值为y_0,y_1,…,y_n ，则该多项式为:P_n(x)=y_0+sum_{i=1}^n[y_i-y_{i-1}]frac{(x-x_0)(x-x_1)cdots (x-x_{i-1})}{(x_i-x_0)(x_i-x_1)cdots(x_i-x_{i-1})}2. 编程实现（1）使用Matlab编程，实现牛顿插值算法。
（2）在给定的函数中，求解函数在[1,2]之间的牛顿插值。
% 目标函数f = @(x) x.*sin(2.*pi.*x);% 样本点xx = [1 2];% 函数值yy = f(xx);% 插值点x = 1.5;% 样例点个数n = length(xx);% 生成差商表for i = 1:(n-1)yy(i+1,:) = diff(yy(1:i+1,:))./diff(xx(1:i+1));end% 计算插值结果yp = yy(1,:);for i = 1:n-1yp = yp +yy(i+1,:).*prod((x-xx(1:i))./(xx(i+1)-xx(1:i)));endfprintf('函数在x=1.5处的值为：%f',yp);三、实验结果通过Matlab编程实现牛顿插值算法，用户给定函数在[1,2]之间的牛顿插值，结果得到：函数在x=1.5处的值为：1.055738。
四、实验结论本次实验通过Matlab实现牛顿插值算法，完成了实验目的，学习利用牛顿插值方法求解函数在指定单点上的值。
数值分析实验报告-插值、三次样条
实验报告：牛顿差值多项式&三次样条... . (1)问题：在区间［-1,1］上分别取n=10、20用两组等距节点对龙格函数f (x)---作多项式插25 x 2值及三次样条插值对每个n值，分别画出插值函数矽(x)的图形。
实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求：1.认真分析问题，深刻理解相关理论知识并能熟练应用；2.编写相关程序并进行实验；3.调试程序，得到最终结果；4.分析解释实验结果；5.按照要求完成实验报告。
实验原理：详见《数值分析第5版》第二章相关容。
实验容：(1)牛顿插值多项式1.1 当 n=10 时：在Matlab下编写代码完成计算和画图。
结果如下：代码：clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.八2);n=length(x1);f=y1(：);for j=2:nfor i=n:-1:jf(i) = (f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25火x八2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式，其结果为：P10（x ）=-220.94*x A10+494.91*x A8-9.5065e-14*x A7-381.43*x A6-8.504e-14*x A5+123.36*x A4+2.0202e-14*x A3-16.855*x A2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在［-1，1］上的图形，并和原函数进行对比（见Fig.1）。
数值分析牛顿插值法实验报告
数值分析牛顿插值法实验报告数值分析牛顿插值法实验报告篇一：数值分析课程实验报告-拉格朗日和牛顿插值法《数值分析》课程实验报告用拉格朗日和牛顿插值法求解函数值算法名称用拉格朗日和牛顿插值法求函数值学科专业机械工程作者姓名程习康作者学号 153711006 作者班级机电院研究生15级C2班中南大学二〇一五年十二月《数值分析》课程实验报告篇二：数值分析实验报告：拉格朗日插值法和牛顿插值法实验一报告拉格朗日插值法一、实验目的1、学习和掌握拉格朗日插值多项式2、运用拉格朗日插值多项式进行计算二、实验原理根据x0,x1,…xn；y0,y1,…yn构造插值多项式其表达式为：将插值点x代入上式，就可得到函数f(x)在点x处的函数值的近似值。
三、运行结果四、代码 using System; using System.Cllectins.Generic; using System.Linq; using System.Text; namespace CnsleApplicatin3 { class Prgram { static duble lglr(duble[] x, duble[] y, duble x1, int n) { duble result = 0.0; fr (int i = 0; i i++) { duble temp = y[i]; fr (int j = 0; j j++) { if (j == i) cntinue; temp = temp * (x1 - x[j]); temp = temp / (x[i] - x[j]); } result = result + temp; } return result; } static vid Main(string[] args) { duble[] x; duble[] y; Cnsle.riteLine( 请输入插值点数：int length = Cnvert.TInt32(Cnsle.ReadLine); x = nei++) { Cnsle.rite( 请输入第{0}个点的x值：, i + 1); x[i] = Cnvert.TDuble(Cnsle.ReadLine);Cnsle.rite( 请输入第{0}个点的y值：, i + 1); y[i] = Cnvert.TDuble(Cnsle.ReadLine); } Cnsle.riteLine( 请输入x1值：duble x1 = Cnvert.TDuble(Cnsle.ReadLine); dubleresult=lglr(x,y,x1,length); Cnsle.rite( 插值计算结果为：{0}：, result); Cnsle.ReadLine; } 牛顿插值法一、实验目的体会并了解牛顿插值法，用计算机插入x值，输出相应的y值。
数值计算实习报告-牛顿插值法
数值计算实习课程设计姓名：张光宇指导教师;谭高山学号：119084169目录1、实验目的2、问题的提出3、牛顿插值法的原理4、差商概念的引出5、牛顿插值公式及其余项的公式6、牛顿插值法计算步骤7、牛顿插值多项式的程序实现8、图像对照牛顿插值多项式9、牛顿插值多项式总结10、附111、附21、实验目的:通过对牛顿插值多项式的Matlab 程序实现,深入了解牛顿插值多项式的原理及编程解决实际问题的能力.2、问题的提出我们知道Lagrange 插值多项式的插值基函数为理论分析中很方便，但是当插值节点增减时全部插值基函数就要随之变化，整个公式也将发生变化，这在实际计算中是很不方便的；Lagrange 插值虽然易算，但若要增加一个节点时，全部基函数 )(x l i 都需重新算过。
3、牛顿插值多项式的原理我们知道两点直线公式)),(),,((11++k k k k y x y x 有：我们考虑点斜式，两点为((x0,y0)(x1,y1))，则直线方程为：那么，在此基础上增加一个节点(x2,y2)，则过这三个点的插值多项式就是：c(x)应该是一个二次多项式。
根据插值条件)(x l j ∏≠=--=nji i i j i x x x x 0)()(11111111()()(()(k kk k k kk kk k k k k ky y L x y x x x x x x x x L x y y x x x x ++++++-=+----=+--点斜式）两点式）1010010()()y y P x y x x x x -=+--21()()()P x P x c x =+2121111()()()()P x P x y P x P x y ====有根据插值条件：可以求出：重新写p2(x)：0101()()0,()()()c x c x c x a x x x x ===--所以221221*********()()()()()()()p x p x y p x a x x x x x x x x --==----21102120001102021010201001011021222021()()()()()()()()()()()()()()()P x P x c x y y y P x y x x x x x x x x x x x x a a x x a x x x x a y y y a x x y P x a x x x x =+--=+-+-----+-+--=-=--=--其中,i x 设插值节点为n i f i ,,1,0, =函数值为222()P x y =有...4、下面引入差商和差分的概念定义：1,,2,1,0,1-=-=+n i x x h i i i iih h max =ni f x P i i ,,1,0,)( ==插值条件为具有如下形式设插值多项式)(x P )())(())(()()(110102010----++--+-+=n n x x x x x x a x x x x a x x a a x P01,,n a a a 其中……为待定系数ni f x P x P i i ,,1,0,)()( ==应满足插值条件000)(a f x P ==00f a =)()(011011x x a a f x P -+==01011x x f f a --=))(()()(12022021022x x x x a x x a a f x P --+-+==12010102022x x x x f f x x f f a ------=ni f x x f i i ,,1,0,)( =处的函数值为在互异的节点设1阶差商2阶差商n+1阶差商可以证明差商具有如下性质:(2) k 阶差商],...,,[21k x x x f 关于节点],...[1,0k x x x 是对称的，或者说均差与节点顺序无关，即均差表零阶均差 一阶均差 二阶均差 三阶均差X 0 f(X 0) X 1 f(X 1) f[X 0, X 1] X 2 f(X 2) f[X 1, X 2] f[X 0,X 1, X 2]X 3 f(X 3) f[X 2, X 3] f[X 1, X 2,X 3]f[X 0,X 1, X 2 X 3]...............),()()(],[j i ji j i j i x x j i x x x f x f x x f ≠≠--=)(],[],[],,[k i x x x x f x x f x x x f ki k j j i k j i ≠--=]1,,1,0[+n x n x x x f ，则由定义[][]110121,,,,,x x x x x f x x x f n n n --≡++ 且的线性组合表示可由函数值阶差商的,)(,),(),(],,,,[)()1(10110k k k x f x f x f x x x x f k x f -],,,,[110k k x x x x f - ∑=+-----=ki k i i i i i i i x x x x x x x x x f 0110)())(()()( []k x x x f ,,,10 [] ==k x x x f ,,,01[]01,,,x x x f k k -=k x5、下面给出牛顿插值公式及其余项的公式： (1) (2)… … … ….........(n+1))1())...((...)2()()1(100+⨯--++⨯-+-n x x x x x x n→))...(](,...,[...))(](,,[)](,[)()(100102100100---+--+-+=n n n x x x x x x f x x x x x x x f x x x x f x f x N 令：))()...(](,...,,[)(100n n n n x x x x x x x x x f x R ---=-则有：)()()(x R x N x f n n +=其中],...,[0i ix x x f a =6、 牛顿插值法计算步骤：牛顿插值法利用函数)(x f 在某区间中若干点的函数值，作出牛顿插值多项式)(x N n ，在这些点上取已知值，在区间的其他点i x 上用牛顿插值多项式的值)(i n x N 作为函数)(i x f 的近似值。
数值分析实验报告-插值、三次样条
实验报告：牛顿差值多项式&三次样条问题：在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值，对每个n 值，分别画出插值函数及()f x 的图形。
实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求：1． 认真分析问题，深刻理解相关理论知识并能熟练应用；2． 编写相关程序并进行实验；3． 调试程序，得到最终结果；4． 分析解释实验结果；5． 按照要求完成实验报告。
实验原理：详见《数值分析 第5版》第二章相关容。
实验容：（1）牛顿插值多项式1.1 当n=10时：在Matlab 下编写代码完成计算和画图。
结果如下：代码：clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p ;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式，其结果为：P10（x）=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.1）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
.
牛顿插值法一、实验目的：学会牛顿插值法，并应用算法于实际问题。
x?x)f(二、实验内容：给定函数，已知：
4832401.2)?.?1449138f(2.f.f(20)?1.414214(2.1)
549193.)?1f(2.4516575(f2.3)?1.
三、实验要求：以此作为函数2.15插值多项式在处的值，用牛顿插值法求4
次Newton（ 1）2.15?N(2.15)。
在MATLAB中用内部函数ezplot绘制出的近似值4次Newton插值多项式的函数图形。
（2）在MATLAB中用内部函数ezplot可直接绘制出以上函数的图形，并与作出的4次Newton插值多项式的图形进行比较。
四、实验过程：
1、编写主函数。
打开Editor编辑器，输入Newton插值法主程序语句：
function [y,L]=newdscg(X,Y,x)
n=length(X); z=x; A=zeros(n,n);A(:,1)=Y';s=0.0; p=1.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
end
C=A(n,n);
for k=(n-1):-1:1
C=conv(C,poly(X(k)));
d=length(C);C(d)=C(d)+A(k,k);
end
y(k)= polyval(C, z);
L(k,:)=poly2sym(C);
0 / 3
.
%%%%%%%%%%%%%%%%%%
t=[2,2.1,2.2,2.3,2.4];
fx=sqrt(t);
wucha=fx-Y;
以文件名newdscg.m保存。
2、运行程序。
（1）在MATLAB命令窗口输入：
>> X=[2,2.1,2.2,2.3,2.4]; Y
=[1.414214,1.449138,1.483240,1.516575,1.549193];
x=2.15;[y,P]=newdscg(X,Y,x)
回车得到：
y =1.4663
wucha =1.0e-06 *
-0.4376 -0.3254 -0.3026 0.0888 0.3385
P = - (4803839603609061*x^4)/2305843009213693952 + (7806239355294329*x^3)/288230376151711744 - (176292469178709*x^2)/1125899906842624 + (1624739243112817*x)/2251799813685248 + 1865116246031207/4503599627370496
（2）在MATLAB命令窗口输入：
>> v=[0,6,-1,3];
>> ezplot(P),axis(v),grid
>> hold on
>> x=0:0.1:6;
>> yt=sqrt(x);plot(x,yt,':')
>> legend('插值效果','原函数')
>> xlabel('X')
>> ylabel('Y')
>>title('Newton插值与原函数比较')
回车即可得到图像1-1。
1 / 3
.
牛顿插值效果图1-1五、实验结果分析：2.15Newton插值多项式在用牛顿插值法求4次的程序可得，由上运行（1）2.15 N(2.15)=1.4663。
处函数的近似值由在MATLAB中用内部函数ezplot直接绘制出出的4次Newton插值图形与原函数的图形知，4次Newton插值图形在区间[0，1]与区间[4，5]内与原函数存在一定的偏差，而在区间[1,4]内误差在10的-6次方，这个精度是非常高的。
因此，在计算区间[1,4]内的值时结果是比较准确的。
2 / 3。