刚体作业
刚体力学作业解答

1 ( MR 2 − mR 2 )ω 2
EK = 1 1 ( MR 2 − mR 2 )ω 2 2 2
4-11 •
30°
设碰后小球速度为v,受杆平均力f,作用时间∆t,则
小球 f∆t = mv − mv0 棒 − fl∆t = Iω − 0 (1) ( 2)
得
mv0 l − mvl = Iω
(3)
F (l1 + l 2 ) − N ′l1 = 0 (a)
Fy
l1
A
N ′
l2
闸 瓦
F
F r′
x
Fx
题图4-4(b)
N
α
Fr
R
N′ =
l1 + l 2 F l1
mg
⋅
O
ω
题图 4-4(c)
N′ =
l1 + l 2 F l1
N
飞轮受到闸瓦的摩擦力为:
l +l Fr = µN = µN ′ = µ 1 2 F l1
r r
α
r T
F = 98 N
m
mg = 98 N
(b)
T
a m
mg
(c)
(a)
题图4 = Jα
M Fr = = 39.2rad ⋅ s − 2 J J
(2)当绳子拉下l=5 m时,飞轮转过的角度 ω 2 = 2αθ =1960
θ=
l = 25rad r
ω = 44.3rad ⋅ s
θ = ω 0 t + αt 2 = 15 × 2π × 7.07 − × 13.3333 × ( π ) 2 = 53 × 2π (rad )
1 2 1 2 9 4
可知在这段时间里,飞轮转了53转. 53 (2)要求飞轮转速在t=2 s内减少一半,可知 ω0 − ω0 ω0 2 α= =− = −7.5πrad ⋅ s − 2
第四章作业解析

直悬挂时质心为重力势能零点。
初态机械能
E0
1 2
J 棒 2
1 6
Ml 22
末态机械能 E Mg l 2
系统机械能守恒,即 E E0
l2
C
则有 1 Ml22 l Mg
6
2
v0 C v0 2
可得 3g
l
带入(1)式
v0
4M 3m
l,可得
v0
4M 3m
3gl
三 计算题
1.一砂轮直径为1m、质量为50kg,以900r/min
小球这一系统
(A) 只有机械能守恒.(B) 只有动量守恒.
(C) 只有对转轴O的角动量守恒.
(D) 机械能、动量和角动量均守恒.[ C ]
解:将杆、小球与作为一个系统
o
系统不受外力矩作用,因此系统
对转轴O的角动量守恒,故选C。
注:小球与杆的外力矩为零,系统角动
量守恒;为非弹性碰撞,机械能不守恒。
二 填空题
统的角动量守恒。
v0 v0 2
将整个过程分为两个阶段:
第一阶段角动量守恒;第二阶段能量守恒
初态角动量(子弹射击棒前的角动量)
L0
J0
1 2
lmv0
m(
l 2
)2
0
m( l )2 2
v0 l2
末态角动量 L L1 L2
射击棒后子弹的角动量
C
l2
v0 C v0 2
L1
J
m( l )2 2
v0 l
空气的摩擦,当两球都滑至杆端时,杆的角速度
为
(A) 20 (C)0 2
(B) 0 (D)0 4
o
d ld
【大题】工科物理大作业04-刚体定轴转动

【大题】工科物理大作业04-刚体定轴转动 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN0404 刚体定轴转动班号 学号 姓名 成绩一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个是正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1.某刚体绕定轴作匀变速转动,对刚体上距转轴为r 处的任一质元来说,在下列关于其法向加速度n a 和切向加速度τa 的表述中,正确的是:A .n a 、τa 的大小均随时间变化;B .n a 、τa 的大小均保持不变;C .n a 的大小变化,τa 的大小保持恒定;D .n a 的大小保持恒定,τa 大小变化。
(C )[知识点]刚体匀变速定轴转动特征,角量与线量的关系。
[分析与题解] 刚体中任一质元的法向、切向加速度分别为 r a n 2ω=,r a τβ=当β = 恒量时,t βωω+=0 ,显然r t r a n 202)(βωω+==,其大小随时间而变,ra τβ=的大小恒定不变。
2. 两个均质圆盘A 和B ,密度分别为ρA 和ρB ,且B ρρ>A ,但两圆盘的质量和厚度相同。
若两盘对通过盘心且与盘面垂直的轴的转动惯量分别为A I 和B I ,则 A .B I I >A; B. B I I <A ;C .B I I =A ; D. 不能确定A I 和B I 的相对大小。
(B )[知识点]转动惯量的计算。
[分析与题解] 设A 、B 两盘厚度为d ,半径分别为R A 和R B ,由题意,二者质量相等,即B B A A d R d R ρπρπ22=因为B A ρρ>, 所以22B A R R < 且转动惯量221mR I =,则B A I I <3.在下列关于刚体的表述中,不正确的是:A .刚体作定轴转动时,其上各点的角速度相同,线速度不同;B .刚体定轴转动的转动定律为βI M =,式中β,,I M 均对同一条固定轴而言的,否则该式不成立;C .对给定的刚体而言,它的质量和形状是一定的,则其转动惯量也是唯一确定的;D .刚体的转动动能等于刚体上各质元的动能之和。
期末复习2(刚体)

10.0 rad/s 方向垂直纸面向外.
2
2分
0112质量为M的匀质圆盘,可绕通过盘中心垂直于盘的固定光滑 轴转动,转动惯量为M r2/2.绕过盘的边缘挂有质量为m,长为l 的匀质柔软绳索(如图).设绳与圆盘无相对滑动,试求当圆盘 两侧绳长之差为S时,绳的加速度的大小.
Mr
a
S
解:选坐标如图所示,任一时刻圆盘两侧的绳长分别为x1、x2 选 长度为x1、x2的两段绳和绕着绳的盘为研究对象.设a为绳的加速 度,β为盘的角加速度,r为盘的半径,为绳的线密度,且在1、 2两点处绳中的张力分别为T1、T2,则 = m / l, a = rβ ① 2分 x2 g-T2 = x2 a ② 1分 T1-x2 g = x1 a ③ 1分 (T1-T2 ) r = ( 1 M+r)r 2β ④ 4分
O m
v
解:碰撞时,系统的角动量守恒
1 2 2 m ' vl ( ml m ' l ) 3
m 'v 1 ( m m ')l 3 15.4rad s
1
m, l
O
m
v
棒转动:用转动定律求解 1 M r ( ml 2 m ' l 2 ) 3 1
2
M = J
-k = J d / dt
d
k dt J
0 / 2
0
1
d
t
0
k dt J
t = (J ln2) / k
(质点与刚体碰撞)
一根放在水平光滑桌面上的匀质棒,可绕通过其一端的 竖直固定光滑轴O转动.棒的质量为m = 1.5 kg,长度为 1 2 l = 1.0 m,对轴的转动惯量为J = 3 ml .初始时棒静 止.今有一水平运动的子弹垂直地射入棒的另一端,并 留在棒中,如图所示.子弹的质量为m= 0.020 kg,速 率为v = 400 m· s-1.试问: (1) 棒开始和子弹一起转动时角速度有多大? (2) 若棒转动时受到大小为Mr = 4.0 N· m的恒定阻力矩 作用,棒能转过多大的角度? m, l
刚体部分作业问题

刚体部分作业问题的研究和解决可 以推动相关领域的技术进步和创新, 促进产业的发展和升级。
02
刚体部分作业问题的基本概念
刚体的定义与特性
刚体的定义
刚体是指在运动过程中,其形状 和大小保持不变,内部任意两点 间的距离始终保持不变的物体。
刚体的特性
刚体具有质量、质心、转动惯量 等物理属性,同时还具有不变形 的特性。
刚体部分作业问
• 刚体部分作业问题概述 • 刚体部分作业问题的基本概念 • 刚体部分作业问题的解决方法 • 刚体部分作业问题的实例分析 • 刚体部分作业问题的未来研究方向
01
刚体部分作业问题概述
定义与特点
定义
刚体部分作业问题是指研究刚体在受 到外力作用时,如何通过改变其内部 结构或布局来达到最优性能或特定目 标的问题。
近似法
近似法是一种通过近似计算来求解问题的方法,适用于 数学模型复杂或精度要求不高的简单问题。
近似法的优点是计算速度快、简便易行,适用于对精度 要求不高的问题。
近似法通常需要使用经验公式或近似公式来简化问题, 通过简化计算过程来快速得到近似解。
近似法的缺点是结果可能存在误差较大,不适用于对精 度要求高的问题。
刚体部分作业问题的实际应用拓展研究
总结词
刚体部分作业问题具有广泛的应用前景,未来研究应 加强其在各个领域的拓展和应用。
详细描述
刚体部分作业问题在机械设计、航空航天、交通运输 、船舶制造等领域具有广泛的应用前景。未来应深入 研究这些领域的具体问题,将刚体部分作业问题的研 究成果应用于实际问题的解决中。同时,应关注新兴 领域的发展动态,积极探索刚体部分作业问题在这些 领域的应用可能性。通过实际应用拓展研究,不断完 善和丰富刚体部分作业问题的理论体系和应用实践。
刚体习题和答案

作业5 刚体力学♫刚体:在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad s ω=,t =20s 时角速度为00.8ωω=,那么飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间飞轮所转过的角度θ= 250rad . 【解答】飞轮作匀变速转动,据0t ωωβ=+,可得出:200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律:定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如下图.绳与轮之间无相对滑动.假设某时刻滑轮沿逆时针方向转动,那么绳中的力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1<m 2),实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得:21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于. (B) 大于,小于2. (C) 大于2. (D) 等于2. 【解答】设飞轮的半径为R ,质量为m ,根据刚体定轴转动定律M J β=,当挂质量为m 的重物是:mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时,有: '2mgR J β=,2'mgRJβ=,比拟二者可得出结论。
面向新世纪课程教材大学物理大作业答案——刚体力学作业
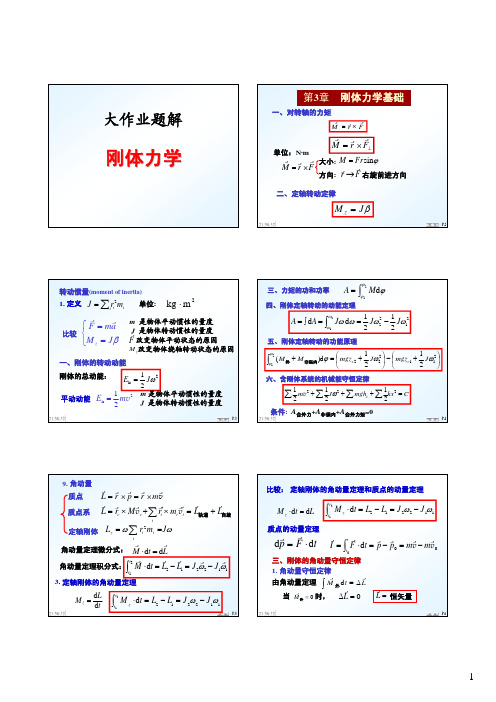
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
刚体的定轴转动习题
WENKU DESIGN
2023-2026
ONE
KEEP VIEW
刚体的定轴转动习
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
https://
CATALOGUE
目 录
• 刚体定轴转动的基本概念 • 刚体定轴转动的力学分析 • 刚体定轴转动的运动分析 • 刚体定轴转动的习题解析 • 刚体定轴转动的实际应用案例
PART 03
刚体定轴转动的运动分析
刚体的角速度与角加速度
角速度
描述刚体转动快慢的物理量,用ω表 示。单位是弧度/秒(rad/s)。
角加速度
描述刚体转动角速度变化快慢的物理 量,用α表示。单
转动轨迹
刚体转动的路径是一个圆或椭圆,其形 状取决于刚体的质量和转动轴的位置。
PART 04
刚体定轴转动的习题解析
简单习题解析
题目
一个质量为m,半径为R的 圆盘,以边缘某点为轴, 以角速度ω做定轴转动, 求圆盘的动量。
解析
根据动量的定义,圆盘的 动量P=mv=mrω,其中r 是质点到转动轴的距离, m是质量,v是线速度,ω 是角速度。
题目
一质量为m的杆,长度为l, 一端固定,绕另一端点做 定轴转动,求杆的转动惯 量。
航空航天器姿态调整中的应用
01
02
03
卫星轨道调整
卫星在轨道调整过程中, 通过刚体定轴转动实现姿 态的调整,从而改变推进 力的方向。
飞机飞行控制
飞机飞行过程中,通过刚 体定轴转动实现舵面的操 纵,从而调整飞行姿态和 方向。
火箭发射
火箭发射过程中,通过刚 体定轴转动实现发动机的 转向和稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题【 B 】1. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ,若A ρ>B ρ,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面的轴的转动惯量各为J A 和J B ,则(A) J A >J B (B) J B >J A (C) J A =J B (D) 不能确定【 C 】2. 有一根水平杆子,一半是铁,一半是木头,长度、截面均相同,可分别绕a ,b ,c 三根竖直轴转动,如图所示。
试问对哪根轴的转动惯量最大(A) a 轴 (B) b 轴 (C) c 轴 (D) 都一样【 A 】3. 如图所示,一摆由质量均为m 的杆与圆盘构成,杆长等于圆盘直径D 的2倍,则摆对通过O 点并与圆盘平面垂直轴的转动惯量为(A) 224177mD (B) 2417mD(C) 224175mD(D) 2617mD【 C 】4. 刚体绕定轴作匀变速转动时,刚体上距转轴为r 的任一点的(A) 切向、法向加速度的大小均随时间变化 (B) 切向、法向加速度的大小均保持恒定(C) 切向加速度的大小恒定,法向加速度的大小变化 (D) 切向加速度的大小变化,法向加速度的大小恒定 【 B 】5. 在下列说法中错误的是(A) 刚体定轴转动时,各质点均绕该轴作圆周运动 (B) 刚体绕定轴匀速转动时,其线速度不变 (C) 力对轴的力矩M的方向与轴平行(D) 处理定轴转动问题时,总要取一个转动平面S ,只有S 面上的分力对轴产生的力矩才对定轴转动有贡献【 C 】6. 下列说法中正确的是(A) 作用在定轴转动刚体上的力越大,刚体转动的角加速度越大(B) 作用在定轴转动刚体上的合力矩越大,刚体转动的角速度越大(C) 作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大(D) 作用在定轴转动刚体上的合力矩为零,刚体转动的角速度为零【 B 】7. 均质细杆可绕过其一端且与杆垂直的水平光滑轴在竖直平面内转动。
今使细杆静止在竖直位置,并给杆一个初速度,使杆在竖直面内绕轴向上转动,在这个过程中(A) 杆的角速度减小,角加速度减小 (B) 杆的角速度减小,角加速度增大(C) 杆的角速度增大,角加速度增大 (D) 杆的角速度增大,角加速度减小【 C 】8. 如图所示,A 、B 为两个相同的绕着轻绳的定滑轮.A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F =Mg .设A 、B 两滑轮的角加速度分别为?A 和?B ,不计滑轮轴的摩擦,则有(A) ?A =?B (B) ?A >?B (C) ?A <?B(D) 开始时?A =?B ,以后?A <?B【 B 】9. 一转动惯量为J 的圆盘绕一固定轴转动,起初角速度为0ω。
设它所受阻力矩与转动角速度成正比,即ωk M -=(k 为正的常数),则圆盘的角速度从0ω变为20ω时所需的时间为(A) 2lnk J (B) 2ln kJ(C) k J ln (D) kJ 1ln【 D 】10. 一质量为m 、半径为R 的均质圆盘,绕过其中心的垂直于盘面的轴转动,由于阻力矩存在,角速度由0ω减小到2/0ω,则圆盘对该轴角动量的增量为(A)0221ωmR (B) 0241ωmR (C) 0221ωmR - (D) 0241ωmR - 【 A 】11. 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为I ,开始时转台以匀角速度?0转动,此时有一质量为m 的人站在转台中心.随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)02ωmR I I + (B) ()02ωR m I I + (C) 02ωmRI(D) 0ω 【 B 】12. 人造地球卫星,绕地球作椭圆轨道运动,如果地球在椭圆的一个焦点上,则卫星的(A) 动量不守恒,动能守恒 (B) 对地心的角动量守恒,动能不守恒(C) 动量守恒,动能不守恒 (D) 对地心的角动量不守恒,动能守恒【 D 】13. 一人站在旋转平台的中央,两臂侧平举,整个系统以2? rad/s 的角速度旋转,转动惯量为 kg ·m 2.如果将双臂收回则系统的转动惯量变为2.0 kg ·m 2.此时系统的转动动能与原来的转动动能之比E k / E k0为(A) 2 (B) 3 (C) 2 (D) 3 【 D 】14. 一个圆盘在水平面内绕一竖直固定轴转动的转动惯量为J ,初始角速度为0ω,后来变为021ω.在上述过程中,阻力矩所作的功为(A) 2041ωJ (B) 2081ωJ - (C) 2041ωJ - (D)283ωJ - 【 B 】15. 有一质量为m 、长为l 的均匀细棒,静止平放在滑动摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动,在转动过程中,细棒受到的摩擦力矩为(A) mgl μ (B) 2mgl μ (C) 3mgl μ (D) 32mglμ【 A 】16. 一质量为m , 长为l 的均质细杆可在水平桌面上绕杆的一端转动, 杆与桌面间的摩擦系数为?, 求摩擦力矩M ? . 先取微元细杆d r , 其质量d m = ?d r = (m /l )d r . 它受的摩擦力是d f ?= ?(d m )g =(?mg /l )d r , 再进行以下的计算(A) M ?=?r d f ?=⎰l r r lmgd μ=?mgl/2O(B) M ?=(?d f ?)l/2=(⎰lr l mgd μ)l/2=?mgl/2(C) M ?=(?d f ?)l/3=(⎰l r l mg0d μ)l/3=?mgl/3(D) M ?=(?d f ?)l =(⎰l r lmg0d μ)l =?mgl【 A 】17. 质量为m 、长为l 的均质细杆,可绕过其一端,与杆垂直的水平轴在竖直平面内转动。
开始杆静止于水平位置,释放后开始向下摆动,在杆摆过2/π的过程中,重力矩对杆的冲量矩为(A)l g ml 3312 (B) l g ml 3322 (C) lgml 32 (D) lgml 3342 【 B 】18. 一根质量为m ,长度为l 的细而均匀的棒,其下端绞接在水平面上,并且竖直的立起,如果让它自由落下,则棒将以角速度ω撞击地面,如图所示。
如果将棒截去一半,初始条件不变,则棒撞击地面的角速度为(A) ω2 (B) ω2 (C) ω (D)2ω【 A 】19. 一根长为l 、质量为m 的均匀细杆,可绕距离其一端4l 的水平轴O 在竖直平面内转动,当杆自由悬挂时,给它一个起始角速度ω,如杆恰能持续转动而不摆动,则(A) lg 734≥ωO 。
(B) lg =ω (C) l g ≥ω (D) lg12≥ω 【 D 】20. 图(a)为一绳长为l 、质量为m 的单摆.图(b)为一长度为l 、质量为m 能绕水平固定轴O 自由转动的匀质细棒.现将单摆和细棒同时从与竖直线成??角度的位置由静止释放,如果运动到竖直位置时,单摆、细棒角速度分别以??1、??2表示.则(A) 2121ωω= (B) 21ωω=(C) 2132ωω= (D) 213/2ωω=二、计算题1. 计算如图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r ,在绳与轮缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,且12m m >.解: 分别以m1,m2滑轮为研究对象,受力图如图(b)所示.对 m1,m2运用牛顿定律, 有m2g?T2?m2a ① T1?m1a ②O(a)(b)θθ对滑轮运用转动定律,有T2r?T1r?(1/2Mr2)? ③又, a?r? ④联立以上4个方程,得a?m2g/m1?m2?M/22. 质量为m,长为l的均匀细棒,可绕垂直于棒的一端的水平轴转动.如将此棒放在水平位置,然后任其落下,求:(1) 当棒转过60°时的角加速度和角速度;(2) 下落到竖直位置时的动能;(3) 下落到竖直位置时的角速度解:(1)棒绕端点的转动惯量J=1/3Ml2由转动定律M=JaM?=Jα可得棒在θ?位置时的角加速度为?3. 一质量为 kg,长为 m 的均匀细棒,支点在棒的上端点,开始时棒自由悬挂.以100 N 的力打击它的下端点,打击时间为 s.(1) 若打击前棒是静止的,求打击时其角动量的变化;(2) 棒的最大偏转角.4. 平板中央开一小孔,质量为m 的小球用细线系住,细线穿过小孔后挂一质量为1M 的重物.小球作匀速圆周运动,当半径为0r 时重物达到平衡.今在1M 的下方再挂一质量为2M 的物体,如图所示.试问这时小球作匀速圆周运动的角速度ω'和半径r '为多少5. 一匀质细棒长度为l ,质量为m ,可绕通过其一端的水平光滑固定轴O 转动,如图所示。
当棒自水平位置由静止摆下时,在竖直位置处与放在地面上的质量也是m 的物体作非弹性碰撞,碰后物体沿地面滑行距离S而静止,设物体与地面间的摩擦系数为μ.求与物体相撞后瞬间棒的角速度.6. 如图所示,质量为M,长为l的均匀直棒,可绕垂直于棒一端的水平轴O无摩擦地转动,它原来静止在平衡位置上.现有一质量为m 的弹性小球飞来,正好在棒的下端与棒垂直地相撞.相撞后,使棒从平衡位置处摆动到最大角度=θ30°处.(1) 设碰撞为弹性碰撞,计算小球初速v的值;(2) 相撞时小球受到多大的冲量。
